第7章平行线的判定专项训练(含解析)
图片预览
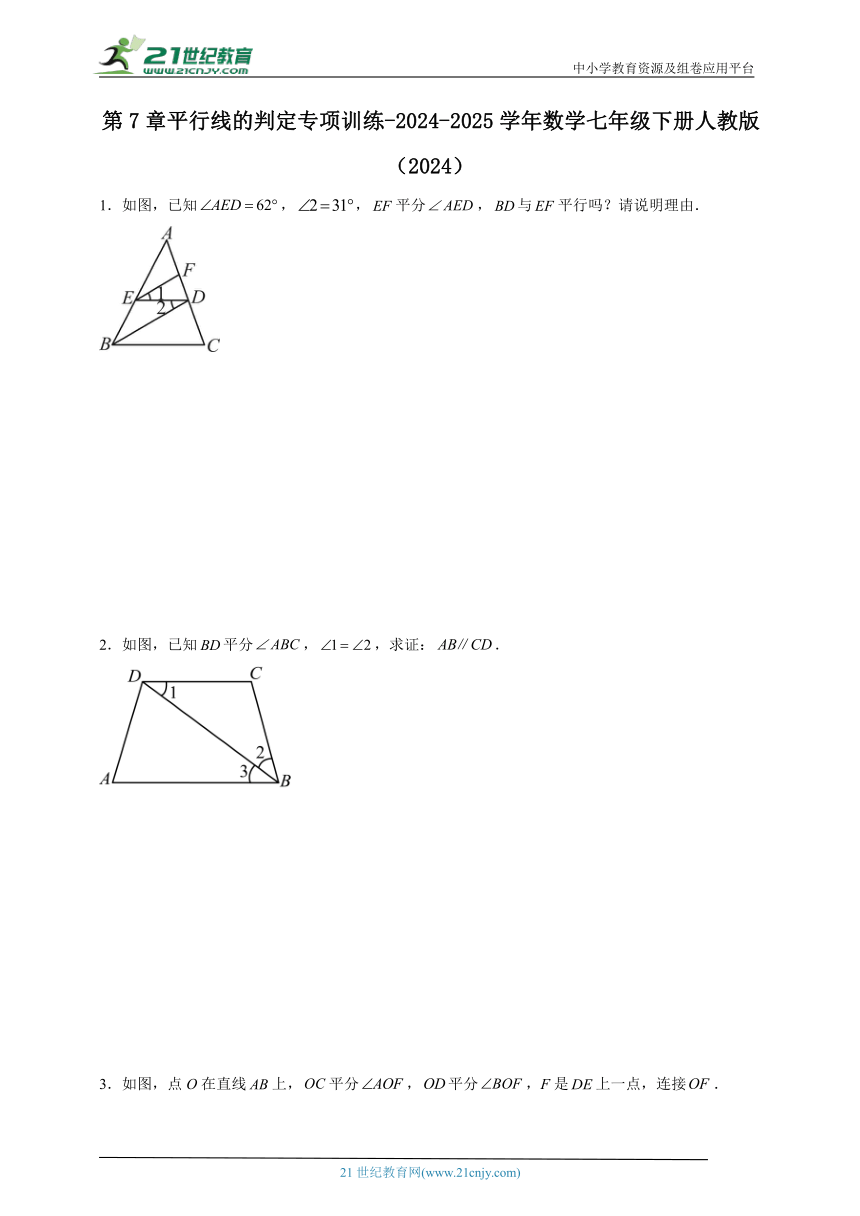



文档简介
中小学教育资源及组卷应用平台
第7章平行线的判定专项训练-2024-2025学年数学七年级下册人教版(2024)
1.如图,已知,,平分,与平行吗?请说明理由.
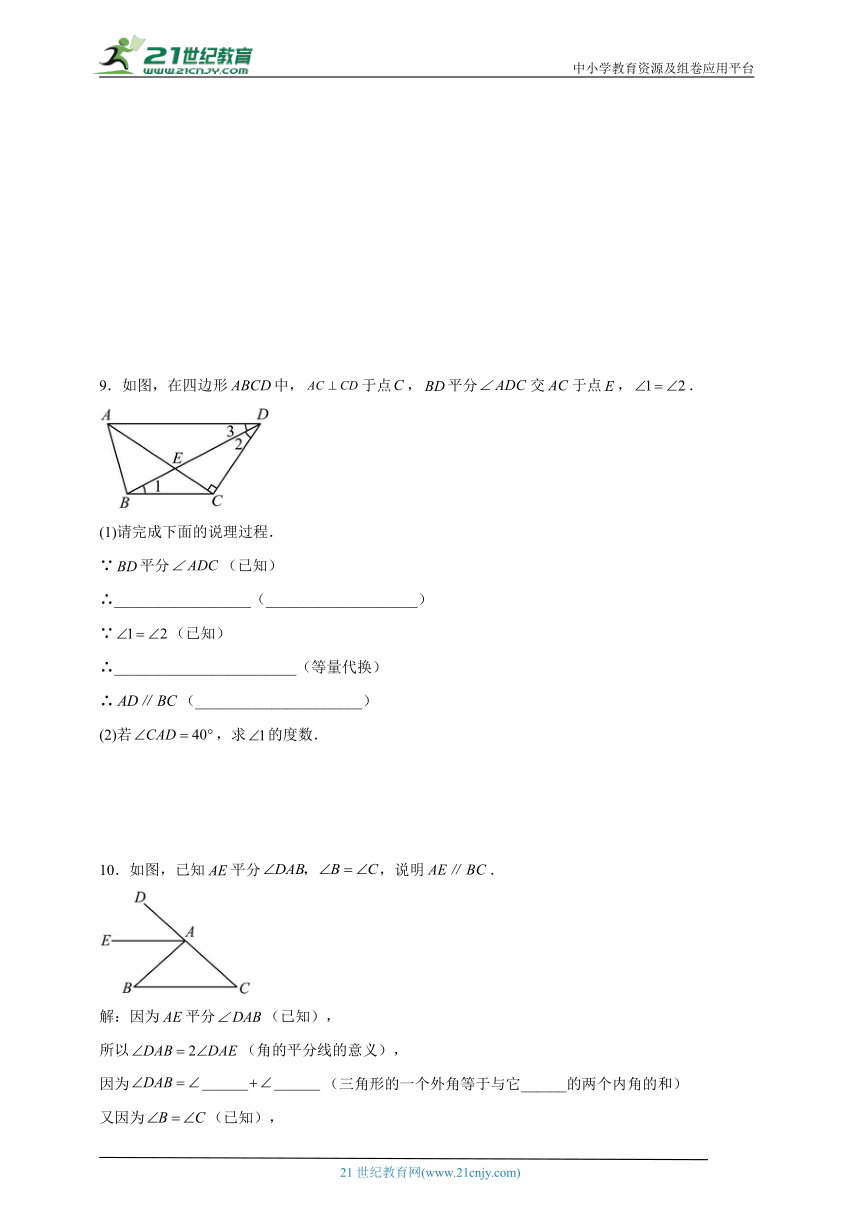
2.如图,已知平分,,求证:.
3.如图,点O在直线上,平分,平分,F是上一点,连接.
(1)求证:;
(2)若与互余,求证:.
4.如图,在三角形中,,垂足为D,,.求证: .
5.如图,分别是的平分线,且.试说明:.
6.如图.
(1)已知,,平分,与平行吗?为什么?
解:.理由如下:
因为,平分(已知),
所以(__________),
又因为(已知),
所以____________________,
所以(__________).
(2)已知,平分,与平行吗?为什么?
7.如图,已知,平分,交直线于点F,若,则与平行吗?请说明理由.
补全以下解题过程:
解:平行.理由如下:
因为,平分,
所以__________=__________°(角平分线的定义)
又因为,
所以____________________,
所以(__________).
8.完成下面的证明:
如图,平分,平分,且.
求证:.
证明:∵平分(已知),
∴( ).
又∵平分( ),
∴______( ).
( ).
又∵(已知),
(______)( ).
∴( ).
9.如图,在四边形中,于点,平分交于点,.
(1)请完成下面的说理过程.
∵平分(已知)
∴__________________(____________________)
∵(已知)
∴________________________(等量代换)
∴(______________________)
(2)若,求的度数.
10.如图,已知平分,说明.
解:因为平分(已知),
所以(角的平分线的意义),
因为(三角形的一个外角等于与它______的两个内角的和)
又因为(已知),
所以______(等式性质),
(完成以下说理过程)
11.已知:如图,平分,,求证:.
证明平分(已知)
______________(__________________)
(已知)
_________(__________________)
(__________________)
12.如图,直线交于点O,分别平分和,已知.
(1)若,求的度数.
(2)试判断与的位置关系,并说明理由;
13.如图,在台球运动中(每次撞击桌边时,撞击前后的路线与桌边所成的夹角相等),如果母球P击中桌边点A,经桌边反弹后击中相邻的另一桌边点B,然后又反弹击中球C.
(1)若,求的度数.
(2)母球P经过的路线与一定平行吗?请说明理由.
14.如图,中,D为上一点,,的角平分线交于点F.
(1)求证:;
(2)G为上一点,当平分,求证:;
(3)在(2)的基础上,连接求证:.
15.如图,,.试说明:.
16.光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有,,请判断光线a与光线b是否平行,并说明理由.
17.如图,是的高,,点、分别在、上,且,试判断与有怎样的位置关系?为什么?
18.如图,已知点E在直线DC上,射线EF平分∠AED,过E点作,G为射线EC上一点,连接BG、AB,且.
(1)试说明;
(2)若试判断AB与EF平行吗?并说明理由.
19.如图、已知,,且线段的延长线平分的邻补角.
(1)求证:;
(2)若射线绕点D以每秒的速度逆时针方向旋转得,同时,射线绕点B以每秒的速度逆时针方向旋转得,和交于点G,设旋转时间为t秒.
①当,且时,求t的值;
②当,,则t的值是___________.
20.(1)我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:___________;
(2)基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”
已知:如图2,∠1和∠2是直线被直线截出的同旁内角,且与互补,求证:.(推理过程请注明理由)
(3)平行线的判定在实际生活中有许多应用:如图3,在铺设铁轨时,两条铁轨必须是互相平行的.将铁轨和枕木看成直线(如图4 所示,直线a、b为直轨,m、n为枕木),是直角,可以通过度量图中已标出的哪个角的度数,来判断两条铁轨是否平行?为什么?
《第7章平行线的判定专项训练-2024-2025学年数学七年级下册人教版(2024)》参考答案
1.平行,见解析
【分析】本题主要考查了平行线的判定方法,也考查了角平分线定义.先由角平分线定义得出,那么,根据内错角相等,两直线平行即可证明.
【详解】解:平行,理由如下:
∵,平分,
∴.
∵,
∴,
∴.
2.证明见解析
【分析】本题主要考查了平行线的判定,角平分线的定义,由角平分线的定义可得,则可得到,再根据内错角相等,两直线平行即可证明结论.
【详解】证明:∵平分,
∴,
∵,
∴,
∴.
3.(1)见解析
(2)见解析
【分析】本题考查与角平分线有关的计算,互余,平行线的判定,熟练掌握平行线的判定定理是解题的关键.
(1)根据角平分线的定义和平角的定义,即可得证;
(2)根据同角的余角相等,得到,即可得证.
【详解】(1)证明:∵平分,平分,
∴,
∵,
∴,
即:,
∴;
(2)证明:∵,
∴,
又∵,
∴,
∴.
4.见解析
【分析】本题主要考查了平行线的判定,同角的余角相等以及垂直的定义,由垂直的定义得出,由已知条件得出,再根据同角的余角相等即可得出,进而可判定.
【详解】证明:∵,
∴(垂直的定义).
∵,.
∴(等量代换).
∴(同角的余角相等).
∴(同位角相等,两直线平行).
5.见解析
【分析】本题考查了平行线,角平行线的综合题,平行线的判定,角平分线定义,将两个角的互补关系转化为两条直线的平行关系是解题的关键.根据角平分线定义,平行线的判定问题可以得证.
【详解】解:分别是的平分线,
.
,
,
.
6.(1)见解析
(2)平行,理由见解析
【分析】本题主要考查角平分线的定义,平行线的判定,掌握平行线的判定方法是解题的关键.
(1)根据角平分线的定义得到,由内错角相等,两直线平行即可求解;
(2)根据同位角相等,两直线平行即可求解.
【详解】(1)解:.理由如下:
∵,平分(已知),
∴(角平分线的定义),
又∵(已知),
∴,
∴(内错角相等,两直线平行).
故答案为:角平分线的定义,,,内错角相等,两直线平行;
(2)解:平行.理由如下:
∵EF平分,
∴,
又∵,
∴,
∴.
7.;60;;;同位角相等,两直线平行
【分析】本题考查了平行线的判定,角平分线的定义,先因为,平分,得,结合,则,即可证明.
【详解】解:解:平行.理由如下:
因为,平分,
所以(角平分线的定义)
又因为,
所以,
所以(同位角相等,两直线平行).
故答案为:;60;;;同位角相等,两直线平行.
8.角平分线的定义;已知;;角平分线的定义;等量代换;;等量代换;同旁内角互补,两直线平行
【分析】本题考查平行线的判定,角平分线定义,根据角平分线的定义以及同旁内角互补,两直线平行,进行作答即可.
【详解】证明:∵平分(已知),
∴(角平分线的定义).
∵平分(已知),
∴(角平分线的定义).
∴(等量代换).
∵(已知),
∴(等量代换).
∴(同旁内角互补,两直线平行).
9.(1)见解析
(2)
【分析】本题考查平行线的判定,与角平分线有关的计算:
(1)根据平行线的判定和性质,进行作答即可;
(2)垂直得到,求出,角平分线求出的度数,进而求出即可.
【详解】(1)∵平分(已知)
∴(角平分线的定义)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行);
(2)∵
∴
∵,
∴
∴
∴.
10.见解析
【分析】本题考查了三角形外角的性质,平行线的判定,角平分线的定义;由平分得;由三角形外角性质,结合,得,从而得,由平行线的判定即可得.
【详解】因为平分(已知),
所以(角的平分线的意义),
因为(三角形的一个外角等于与它不相邻的两个内角的和)
又因为(已知),
所以(等式性质),
所以,
所以.
故答案为:;不相邻;
11.见解析
【分析】本题考查平行线的判定,角平分线的定义,根据角平分线的定义,等量代换,平行线的判定方法,进行作答即可.
【详解】证明平分(已知)
∴(角平分线的定义)
(已知)
(等量代换)
(内错角相等,两直线平行).
12.(1)
(2),理由见解析
【分析】本题考查与角平分线有关的计算,平行线的判定,找准角度之间的等量关系,是解题的关键.
(1)根据角平分线平分角,得到,结合平角的定义和,进行求解即可;
(2)角平分线平分角,结合平角的定义推出,推出,即可得出结论.
【详解】(1)解:∵平分,
∴,
∵,
∴设,则:,
∴,
∵,
∴,
∴;
(2),理由如下:
∵分别平分和,
∴,
∵,
∴,
∵,
∴,
∴.
13.(1)
(2)与一定平行,理由见解析
【分析】本题考查了平行线的判定,平角的性质,正确掌握相关性质是解题的关键.
(1)先得出,再根据平角定义,得,代入数值进行计算,即可作答.
(2)与(1)同理,得,,再结合,进行角的等量代换,即可作答.
【详解】(1)解:∵每次撞击桌边时,撞击前后的路线与桌边所成的夹角相等,
∴,,
∵,
∴.
(2)解:与一定平行.
理由:因为,,
所以.
同理可得.
因为,
所以,
所以.
14.(1)见解析
(2)见解析
(3)见解析
【分析】利用三角形外角的性质得, 从而证明结论;
利用内错角相等,两直线平行证明即可;
利用证明,得到,然后再利用证明,从而得出结论.
【详解】(1)证明: ∵是的角平分线,
∴,
∵分别是的外角,
∴,
又∵,
∴;
(2)证明:∵平分,
∴,
又∵,
∴,
∴;
(3)
∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴,
又∵,,
∴,
∴.
【点睛】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明是解题的关键.
15.见解析
【分析】先由等量代换得,再根据内角错相等,两直线平行可得.
【详解】证明: 且 ,
,
(内错角相等,两直线平行).
【点睛】本题考查平行线的判定,掌握平行线的判定定理是解决此题的关键.
16.平行,理由见解析
【分析】根据等角的补角相等求出与的补角相等,再根据,结合内错角相等,两直线平行即可判定.
【详解】解:平行,理由如下:
如图,,
,
,
,
.
【点睛】本题考查了平行线的判定,解决本题的关键是掌握平行线的判定.
17.,见解析
【分析】由两直线平行内错角相等得到,结合得到,再由同旁内角互补,两直线平行得到,最后根据同一平面内,垂直于同一条直线的两条直线平行解答即可.
【详解】解:,理由如下,
,
.
,
.
是的高,
,
.
【点睛】本题考查平行线的判定与性质,是重要考点,掌握相关知识是解题关键.
18.(1)见解析
(2)ABEF,理由见解析
【分析】(1)根据互相垂直的意义,以及同角或等角的余角或补角相等,得出结论;
(2)根据角平分线以及同角或等角的余角或补角相等,得出∠A=∠AEF,利用内错角相等两直线平行,得出结论.
【详解】(1)解:∵,
∴,
∴,
∵,
∴;
(2)解: ,
理由如下:
∵平分 ,
∴,
∵,,
∴,
又∵ ,
∴,
∴ .
【点睛】本题考查平行线的判定定理,同角(或等角)的余角相等,角平分线的有关证明,能根据同角(或等角)的余角相等完成角度之间的转化是解题关键.
19.(1)见解析
(2)①;②32或50
【分析】(1)先求出,再由角平分线的定义得到,则,由此即可证明;
(2)①如图所示,过点G作,则,由平行线的性质得到,,则,再由
, 得到,解方程即可;②分图2-1和图2-2,过点G作,则,利用平行线的性质求出,的度数,然后根据建立方程求解即可.
【详解】(1)证明:∵是的邻补角,,
∴,
又∵平分.
∴,
又∵,
∴,
∴;
(2)解:①∵
∴,
如图所示,过点G作,
又∵
∴,
∴,,
∴
又∵,
∴,
∴;
②如图2-1所示,当时,过点G作,
又∵
∴,
∴,,
∴,
∵,
∴,
解得;
如图2-2所示,
由(2)①,
∴,
∵,
∴
解得;
综上所述,t的值为或50.
【点睛】本题主要考查了平行线的性质,角平分线定义,利用分类讨论的思想是解题的关键.
20.(1)同位角相等,两直线平行;(2)见解析;(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;见解析
【分析】(1)依据同位角相等,两直线平行作答;
(2)根据同角的补角相等可得,再根据同位角相等,两直线平行作答即可;
(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;然后利用(1)的基本事实和(2)的结论证明即可.
【详解】(1)用移动三角尺的方法画出了两条平行线,依据的基本事实为:同位角相等,两直线平行;
故答案为:同位角相等,两直线平行;
(2)证明:如图2,∵与互补,即(补角的定义),
又∵(邻补角的定义),
∴(同角的补角相等),
∴(同位角相等,两直线平行);
(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;
理由:∵是直角,
∴,
若,则,由(2)同旁内角互补,两直线平行可知;
若,则,根据同位角相等,两直线平行可知;
若,由于,则,根据同位角相等,两直线平行可知.
【点睛】本题考查了平行线的判定和演绎推理,正确理解题意、熟知同位角相等、两直线平行是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第7章平行线的判定专项训练-2024-2025学年数学七年级下册人教版(2024)
1.如图,已知,,平分,与平行吗?请说明理由.
2.如图,已知平分,,求证:.
3.如图,点O在直线上,平分,平分,F是上一点,连接.
(1)求证:;
(2)若与互余,求证:.
4.如图,在三角形中,,垂足为D,,.求证: .
5.如图,分别是的平分线,且.试说明:.
6.如图.
(1)已知,,平分,与平行吗?为什么?
解:.理由如下:
因为,平分(已知),
所以(__________),
又因为(已知),
所以____________________,
所以(__________).
(2)已知,平分,与平行吗?为什么?
7.如图,已知,平分,交直线于点F,若,则与平行吗?请说明理由.
补全以下解题过程:
解:平行.理由如下:
因为,平分,
所以__________=__________°(角平分线的定义)
又因为,
所以____________________,
所以(__________).
8.完成下面的证明:
如图,平分,平分,且.
求证:.
证明:∵平分(已知),
∴( ).
又∵平分( ),
∴______( ).
( ).
又∵(已知),
(______)( ).
∴( ).
9.如图,在四边形中,于点,平分交于点,.
(1)请完成下面的说理过程.
∵平分(已知)
∴__________________(____________________)
∵(已知)
∴________________________(等量代换)
∴(______________________)
(2)若,求的度数.
10.如图,已知平分,说明.
解:因为平分(已知),
所以(角的平分线的意义),
因为(三角形的一个外角等于与它______的两个内角的和)
又因为(已知),
所以______(等式性质),
(完成以下说理过程)
11.已知:如图,平分,,求证:.
证明平分(已知)
______________(__________________)
(已知)
_________(__________________)
(__________________)
12.如图,直线交于点O,分别平分和,已知.
(1)若,求的度数.
(2)试判断与的位置关系,并说明理由;
13.如图,在台球运动中(每次撞击桌边时,撞击前后的路线与桌边所成的夹角相等),如果母球P击中桌边点A,经桌边反弹后击中相邻的另一桌边点B,然后又反弹击中球C.
(1)若,求的度数.
(2)母球P经过的路线与一定平行吗?请说明理由.
14.如图,中,D为上一点,,的角平分线交于点F.
(1)求证:;
(2)G为上一点,当平分,求证:;
(3)在(2)的基础上,连接求证:.
15.如图,,.试说明:.
16.光线从空气中射入水中会产生折射现象,同时光线从水中射入空气中也会产生折射现象,如图,光线a从空气中射入水中,再从水中射入空气中,形成光线b,根据光学知识有,,请判断光线a与光线b是否平行,并说明理由.
17.如图,是的高,,点、分别在、上,且,试判断与有怎样的位置关系?为什么?
18.如图,已知点E在直线DC上,射线EF平分∠AED,过E点作,G为射线EC上一点,连接BG、AB,且.
(1)试说明;
(2)若试判断AB与EF平行吗?并说明理由.
19.如图、已知,,且线段的延长线平分的邻补角.
(1)求证:;
(2)若射线绕点D以每秒的速度逆时针方向旋转得,同时,射线绕点B以每秒的速度逆时针方向旋转得,和交于点G,设旋转时间为t秒.
①当,且时,求t的值;
②当,,则t的值是___________.
20.(1)我们曾用移动三角尺的方法画出了两条平行线(如图1),请说明依据的基本事实为:___________;
(2)基本事实可作为依据,用来证明新的结论.请根据以上基本事实证明平行线的判定方法:“同旁内角互补,两直线平行”
已知:如图2,∠1和∠2是直线被直线截出的同旁内角,且与互补,求证:.(推理过程请注明理由)
(3)平行线的判定在实际生活中有许多应用:如图3,在铺设铁轨时,两条铁轨必须是互相平行的.将铁轨和枕木看成直线(如图4 所示,直线a、b为直轨,m、n为枕木),是直角,可以通过度量图中已标出的哪个角的度数,来判断两条铁轨是否平行?为什么?
《第7章平行线的判定专项训练-2024-2025学年数学七年级下册人教版(2024)》参考答案
1.平行,见解析
【分析】本题主要考查了平行线的判定方法,也考查了角平分线定义.先由角平分线定义得出,那么,根据内错角相等,两直线平行即可证明.
【详解】解:平行,理由如下:
∵,平分,
∴.
∵,
∴,
∴.
2.证明见解析
【分析】本题主要考查了平行线的判定,角平分线的定义,由角平分线的定义可得,则可得到,再根据内错角相等,两直线平行即可证明结论.
【详解】证明:∵平分,
∴,
∵,
∴,
∴.
3.(1)见解析
(2)见解析
【分析】本题考查与角平分线有关的计算,互余,平行线的判定,熟练掌握平行线的判定定理是解题的关键.
(1)根据角平分线的定义和平角的定义,即可得证;
(2)根据同角的余角相等,得到,即可得证.
【详解】(1)证明:∵平分,平分,
∴,
∵,
∴,
即:,
∴;
(2)证明:∵,
∴,
又∵,
∴,
∴.
4.见解析
【分析】本题主要考查了平行线的判定,同角的余角相等以及垂直的定义,由垂直的定义得出,由已知条件得出,再根据同角的余角相等即可得出,进而可判定.
【详解】证明:∵,
∴(垂直的定义).
∵,.
∴(等量代换).
∴(同角的余角相等).
∴(同位角相等,两直线平行).
5.见解析
【分析】本题考查了平行线,角平行线的综合题,平行线的判定,角平分线定义,将两个角的互补关系转化为两条直线的平行关系是解题的关键.根据角平分线定义,平行线的判定问题可以得证.
【详解】解:分别是的平分线,
.
,
,
.
6.(1)见解析
(2)平行,理由见解析
【分析】本题主要考查角平分线的定义,平行线的判定,掌握平行线的判定方法是解题的关键.
(1)根据角平分线的定义得到,由内错角相等,两直线平行即可求解;
(2)根据同位角相等,两直线平行即可求解.
【详解】(1)解:.理由如下:
∵,平分(已知),
∴(角平分线的定义),
又∵(已知),
∴,
∴(内错角相等,两直线平行).
故答案为:角平分线的定义,,,内错角相等,两直线平行;
(2)解:平行.理由如下:
∵EF平分,
∴,
又∵,
∴,
∴.
7.;60;;;同位角相等,两直线平行
【分析】本题考查了平行线的判定,角平分线的定义,先因为,平分,得,结合,则,即可证明.
【详解】解:解:平行.理由如下:
因为,平分,
所以(角平分线的定义)
又因为,
所以,
所以(同位角相等,两直线平行).
故答案为:;60;;;同位角相等,两直线平行.
8.角平分线的定义;已知;;角平分线的定义;等量代换;;等量代换;同旁内角互补,两直线平行
【分析】本题考查平行线的判定,角平分线定义,根据角平分线的定义以及同旁内角互补,两直线平行,进行作答即可.
【详解】证明:∵平分(已知),
∴(角平分线的定义).
∵平分(已知),
∴(角平分线的定义).
∴(等量代换).
∵(已知),
∴(等量代换).
∴(同旁内角互补,两直线平行).
9.(1)见解析
(2)
【分析】本题考查平行线的判定,与角平分线有关的计算:
(1)根据平行线的判定和性质,进行作答即可;
(2)垂直得到,求出,角平分线求出的度数,进而求出即可.
【详解】(1)∵平分(已知)
∴(角平分线的定义)
∵(已知)
∴(等量代换)
∴(内错角相等,两直线平行);
(2)∵
∴
∵,
∴
∴
∴.
10.见解析
【分析】本题考查了三角形外角的性质,平行线的判定,角平分线的定义;由平分得;由三角形外角性质,结合,得,从而得,由平行线的判定即可得.
【详解】因为平分(已知),
所以(角的平分线的意义),
因为(三角形的一个外角等于与它不相邻的两个内角的和)
又因为(已知),
所以(等式性质),
所以,
所以.
故答案为:;不相邻;
11.见解析
【分析】本题考查平行线的判定,角平分线的定义,根据角平分线的定义,等量代换,平行线的判定方法,进行作答即可.
【详解】证明平分(已知)
∴(角平分线的定义)
(已知)
(等量代换)
(内错角相等,两直线平行).
12.(1)
(2),理由见解析
【分析】本题考查与角平分线有关的计算,平行线的判定,找准角度之间的等量关系,是解题的关键.
(1)根据角平分线平分角,得到,结合平角的定义和,进行求解即可;
(2)角平分线平分角,结合平角的定义推出,推出,即可得出结论.
【详解】(1)解:∵平分,
∴,
∵,
∴设,则:,
∴,
∵,
∴,
∴;
(2),理由如下:
∵分别平分和,
∴,
∵,
∴,
∵,
∴,
∴.
13.(1)
(2)与一定平行,理由见解析
【分析】本题考查了平行线的判定,平角的性质,正确掌握相关性质是解题的关键.
(1)先得出,再根据平角定义,得,代入数值进行计算,即可作答.
(2)与(1)同理,得,,再结合,进行角的等量代换,即可作答.
【详解】(1)解:∵每次撞击桌边时,撞击前后的路线与桌边所成的夹角相等,
∴,,
∵,
∴.
(2)解:与一定平行.
理由:因为,,
所以.
同理可得.
因为,
所以,
所以.
14.(1)见解析
(2)见解析
(3)见解析
【分析】利用三角形外角的性质得, 从而证明结论;
利用内错角相等,两直线平行证明即可;
利用证明,得到,然后再利用证明,从而得出结论.
【详解】(1)证明: ∵是的角平分线,
∴,
∵分别是的外角,
∴,
又∵,
∴;
(2)证明:∵平分,
∴,
又∵,
∴,
∴;
(3)
∵平分,
∴,
∵,
∴,
在和中,
,
∴,
∴,
又∵,,
∴,
∴.
【点睛】本题主要考查了全等三角形的判定与性质,三角形外角的性质等知识,证明是解题的关键.
15.见解析
【分析】先由等量代换得,再根据内角错相等,两直线平行可得.
【详解】证明: 且 ,
,
(内错角相等,两直线平行).
【点睛】本题考查平行线的判定,掌握平行线的判定定理是解决此题的关键.
16.平行,理由见解析
【分析】根据等角的补角相等求出与的补角相等,再根据,结合内错角相等,两直线平行即可判定.
【详解】解:平行,理由如下:
如图,,
,
,
,
.
【点睛】本题考查了平行线的判定,解决本题的关键是掌握平行线的判定.
17.,见解析
【分析】由两直线平行内错角相等得到,结合得到,再由同旁内角互补,两直线平行得到,最后根据同一平面内,垂直于同一条直线的两条直线平行解答即可.
【详解】解:,理由如下,
,
.
,
.
是的高,
,
.
【点睛】本题考查平行线的判定与性质,是重要考点,掌握相关知识是解题关键.
18.(1)见解析
(2)ABEF,理由见解析
【分析】(1)根据互相垂直的意义,以及同角或等角的余角或补角相等,得出结论;
(2)根据角平分线以及同角或等角的余角或补角相等,得出∠A=∠AEF,利用内错角相等两直线平行,得出结论.
【详解】(1)解:∵,
∴,
∴,
∵,
∴;
(2)解: ,
理由如下:
∵平分 ,
∴,
∵,,
∴,
又∵ ,
∴,
∴ .
【点睛】本题考查平行线的判定定理,同角(或等角)的余角相等,角平分线的有关证明,能根据同角(或等角)的余角相等完成角度之间的转化是解题关键.
19.(1)见解析
(2)①;②32或50
【分析】(1)先求出,再由角平分线的定义得到,则,由此即可证明;
(2)①如图所示,过点G作,则,由平行线的性质得到,,则,再由
, 得到,解方程即可;②分图2-1和图2-2,过点G作,则,利用平行线的性质求出,的度数,然后根据建立方程求解即可.
【详解】(1)证明:∵是的邻补角,,
∴,
又∵平分.
∴,
又∵,
∴,
∴;
(2)解:①∵
∴,
如图所示,过点G作,
又∵
∴,
∴,,
∴
又∵,
∴,
∴;
②如图2-1所示,当时,过点G作,
又∵
∴,
∴,,
∴,
∵,
∴,
解得;
如图2-2所示,
由(2)①,
∴,
∵,
∴
解得;
综上所述,t的值为或50.
【点睛】本题主要考查了平行线的性质,角平分线定义,利用分类讨论的思想是解题的关键.
20.(1)同位角相等,两直线平行;(2)见解析;(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;见解析
【分析】(1)依据同位角相等,两直线平行作答;
(2)根据同角的补角相等可得,再根据同位角相等,两直线平行作答即可;
(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;然后利用(1)的基本事实和(2)的结论证明即可.
【详解】(1)用移动三角尺的方法画出了两条平行线,依据的基本事实为:同位角相等,两直线平行;
故答案为:同位角相等,两直线平行;
(2)证明:如图2,∵与互补,即(补角的定义),
又∵(邻补角的定义),
∴(同角的补角相等),
∴(同位角相等,两直线平行);
(3)可以通过度量图中已标出或或的度数,看它们是否等于,来判断两条铁轨平行;
理由:∵是直角,
∴,
若,则,由(2)同旁内角互补,两直线平行可知;
若,则,根据同位角相等,两直线平行可知;
若,由于,则,根据同位角相等,两直线平行可知.
【点睛】本题考查了平行线的判定和演绎推理,正确理解题意、熟知同位角相等、两直线平行是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
