2025年浙江省中考数学模拟试卷(4)(含解析)
文档属性
| 名称 | 2025年浙江省中考数学模拟试卷(4)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 17:23:45 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年浙江省中考数学模拟试卷(4)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 厦门模拟)用数轴上的点表示下列各数,其中与原点距离最远的点表示的数是( )
A.0 B.1 C.2 D.﹣3
2.(2025 尉氏县一模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B. C. D.
3.(2025 泰安模拟)ChatGPT是人工智能研究实验室OpenAI新推出的一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A.1.75×103 B.1.75×1012 C.1750×108 D.1.75×1011
4.(2025 亳州二模)下列运算正确的是( )
A.a2 a3=a6 B.(ab)2=ab2 C.(a3)2=a5 D.a7÷a3=a4
5.(2025 成都模拟)为响应习近平总书记强调的“着眼满足人民群众多样化、多层次、多方面的精神文化需求”这一号召,某市夜校开设漆扇制作课程,一周内每天报名的人数分别为:72,86,67,59,91,82,94,则这组数据的中位数是( )
A.59 B.67 C.82 D.86
6.(2025 浙江模拟)如图,若△ABC与△A'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
7.(2025 宿城区一模)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B. C. D.
8.(2025 临夏州一模)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=2,BN=4,则BD的长为( )
A. B. C. D.
9.(2025 浙江一模)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,且x3<x2<x1,下列正确的选项是( )
A.若y3<y1<y2,则x1 x2 x3>0 B.若y2<y3<y1,则x1 x2 x3<0
C.若y2<y1<y3,则x1 x2 x3>0 D.若y1<y3<y2,则x1 x2 x3>0
10.(2025 德阳模拟)如图,在正方形ABCD中,点E、F分别在AB、BC上,连接AF,过点E作EG⊥AF交CD于点G,连接FG.若AE=2BF,∠BAF=α,则∠EGF一定等于( )
A.45°+α B.45°﹣α C.2α D.α
二、填空题:本题共6小题,每小题3分,共18分。
11.(2025 楚雄州一模)分解因式:m2﹣9m= .
12.(2025 新郑市模拟)方程组的解为 .
13.(2025 余姚市一模)某校运会百米预赛用抽签方式确定赛道,8条赛道的编号分别为1到8.若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是 .
14.(2025 衢州一模)如图,直线BC与⊙O相切于点C,点A在⊙O上,AB⊥BC于点B.若AB=3,BC=6,则⊙O的半径为 cm.
15.(2025 苏州一模)二次函数y=ax2+bx+c(其中a,b,c为常数,且a≠0)的图象以点A(1,m),B(3,m),C(0,﹣m),其中m为常数,且m≠0,则方程ax2+bx﹣2c=0的解为 .
16.(2025 温州一模)如图,点E,F分别在 ABCD的边AB,CD上,连结DE,EF,点D关于EF的对称点G恰好在AB的延长线上,连结FG交BC于点H.若,CF=1,则= ,AE= .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(2025 襄州区二模)计算:.
18.(2025 扬州模拟)解不等式组:,并在数轴上表示解集.
19.(2024 普陀区二模)如图,在△ABC中,∠B=2∠C,点D在边BC上,AB=AD=13,BC=23.
(1)求BD的长;
(2)求tanC的值.
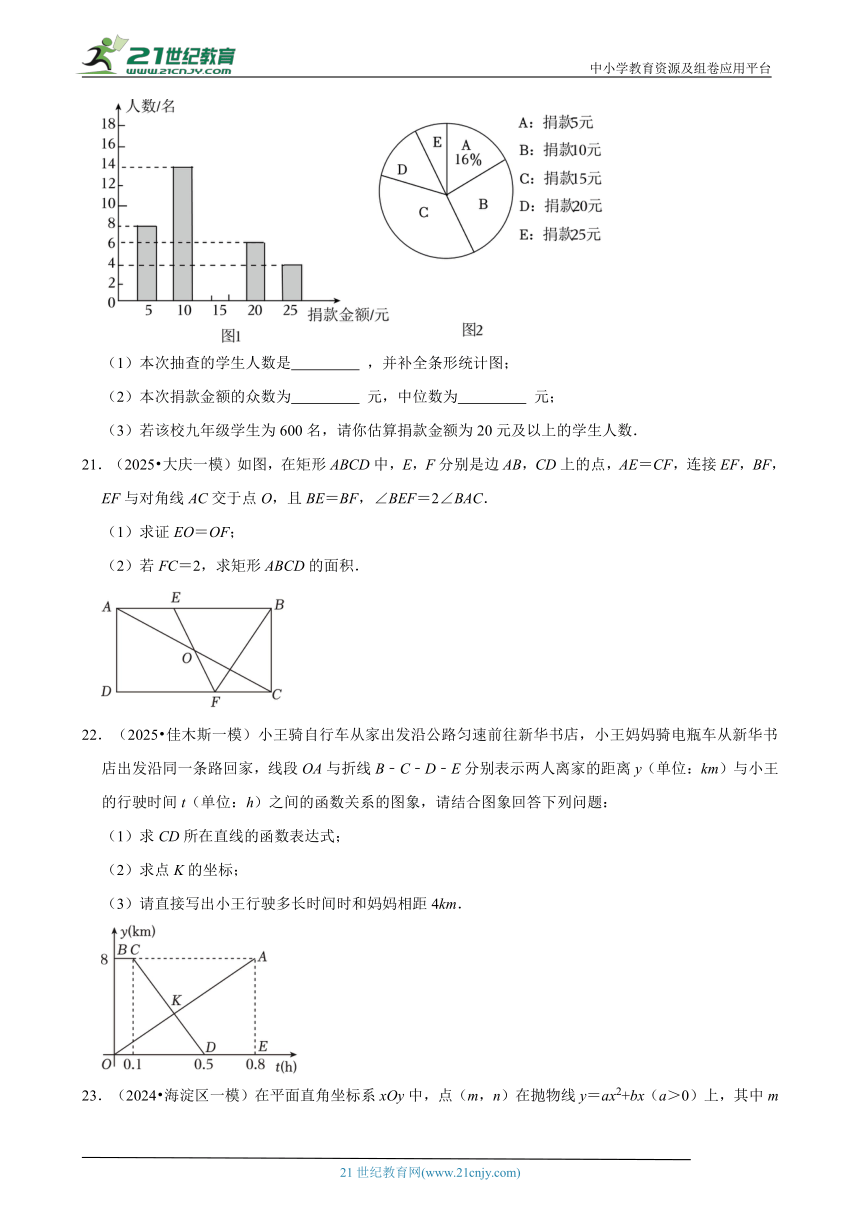
20.(2025 西和县模拟)为弘扬向善、为善的优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,九年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)本次捐款金额的众数为 元,中位数为 元;
(3)若该校九年级学生为600名,请你估算捐款金额为20元及以上的学生人数.
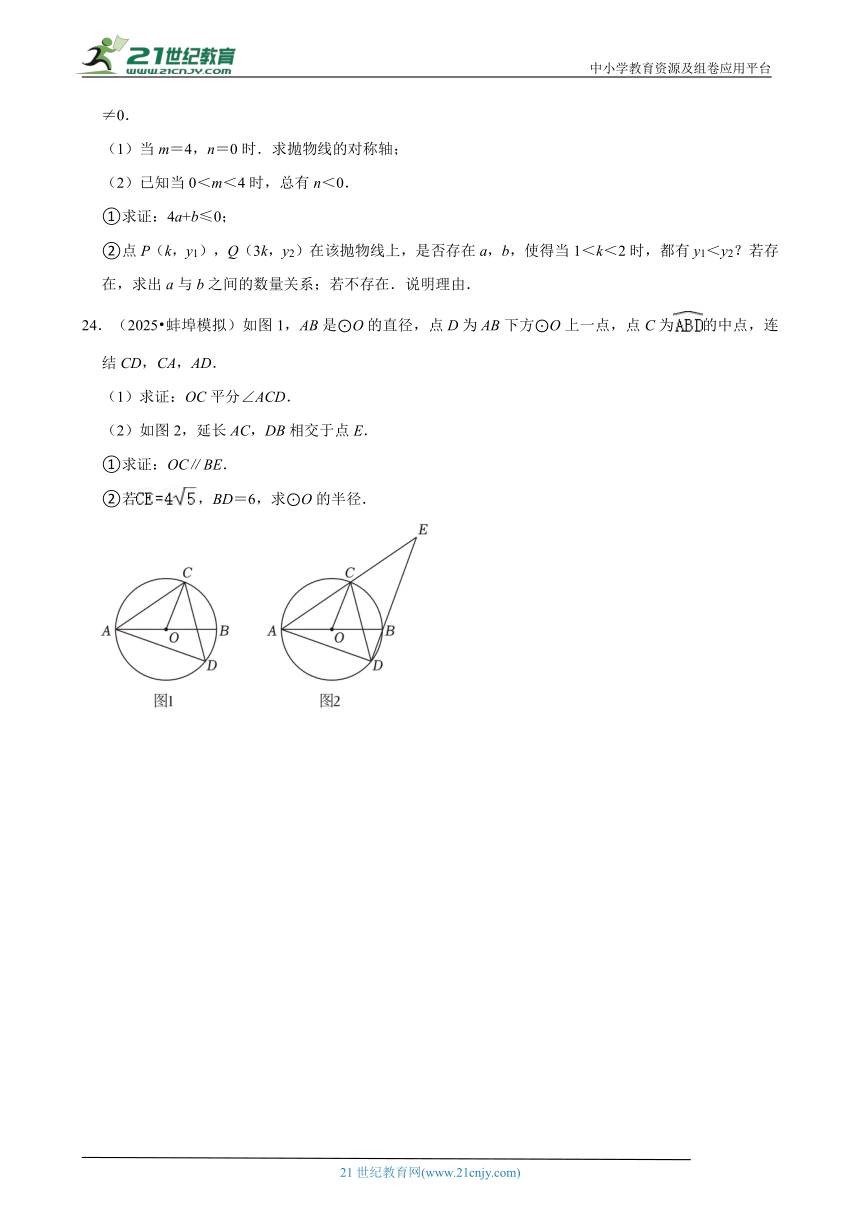
21.(2025 大庆一模)如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证EO=OF;
(2)若FC=2,求矩形ABCD的面积.
22.(2025 佳木斯一模)小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(单位:km)与小王的行驶时间t(单位:h)之间的函数关系的图象,请结合图象回答下列问题:
(1)求CD所在直线的函数表达式;
(2)求点K的坐标;
(3)请直接写出小王行驶多长时间时和妈妈相距4km.
23.(2024 海淀区一模)在平面直角坐标系xOy中,点(m,n)在抛物线y=ax2+bx(a>0)上,其中m≠0.
(1)当m=4,n=0时.求抛物线的对称轴;
(2)已知当0<m<4时,总有n<0.
①求证:4a+b≤0;
②点P(k,y1),Q(3k,y2)在该抛物线上,是否存在a,b,使得当1<k<2时,都有y1<y2?若存在,求出a与b之间的数量关系;若不存在.说明理由.
24.(2025 蚌埠模拟)如图1,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连结CD,CA,AD.
(1)求证:OC平分∠ACD.
(2)如图2,延长AC,DB相交于点E.
①求证:OC∥BE.
②若,BD=6,求⊙O的半径.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 厦门模拟)用数轴上的点表示下列各数,其中与原点距离最远的点表示的数是( )
A.0 B.1 C.2 D.﹣3
【点拨】到原点距离最远的点,即绝对值最大的点,首先求出各个数的绝对值,即可作出判断.
【解析】解:∵0、1、2、﹣3四个点所表示的有理数的绝对值分别为0、1、2、3,其中绝对值最大的是﹣3,
∴与原点距离最远的点表示的数是﹣3.
故选:D.
【点睛】本题考查了数轴,解题的关键是掌握数轴知识.
2.(2025 尉氏县一模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B. C. D.
【点拨】根据俯视图是从上面看到的图形进行求解即可.
【解析】解:从上面看,看到的图形为一个正方形,在这个正方形里面还有一个小正方形,即看到的图形为,
故选C.
【点睛】本题主要考查了简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
3.(2025 泰安模拟)ChatGPT是人工智能研究实验室OpenAI新推出的一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A.1.75×103 B.1.75×1012 C.1750×108 D.1.75×1011
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:175000000000=1.75×1011.
故选:D.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2025 亳州二模)下列运算正确的是( )
A.a2 a3=a6 B.(ab)2=ab2 C.(a3)2=a5 D.a7÷a3=a4
【点拨】根据同底数幂相乘,底数不变,指数相加;积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减;对各选项分析判断后利用排除法求解.
【解析】解:A、a2 a3=a5,故此选项不符合题意;
B、(ab)2=a2b2,故此选项不符合题意;
C、(a3)2=a6,故此选项不符合题意;
D、a7÷a3=a4,故此选项符合题意;
故选:D.
【点睛】本题考查了同底数幂的乘法、幂的乘方与积的乘方、同底数幂的除法,熟练掌握运算法则是解题的关键.
5.(2025 成都模拟)为响应习近平总书记强调的“着眼满足人民群众多样化、多层次、多方面的精神文化需求”这一号召,某市夜校开设漆扇制作课程,一周内每天报名的人数分别为:72,86,67,59,91,82,94,则这组数据的中位数是( )
A.59 B.67 C.82 D.86
【点拨】利用中位数的定义求解即可.
【解析】解:将数据按照从小到大的顺序排列:59,67,72,82,86,91,94,
一共有7个数,处在中间位置的数是82,
∴这组数据的中位数是82.
故选:C.
【点睛】本题主要考查了中位数的概念,正确理解中位数的概念是解题的关键.
6.(2025 浙江模拟)如图,若△ABC与△A'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
【点拨】根据位似的两个图形对应点的连线都经过同一点解答.
【解析】解:延长A′A、B′B交于点P,
则点P(1,﹣1)为位似中心,
故选:A.
【点睛】本题考查的是位似变换的概念,掌握位似的两个图形是相似形、对应点的连线都经过同一点是解题的关键.
7.(2025 宿城区一模)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B. C. D.
【点拨】首先设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得等量关系:慢马速度×2=快马速度,根据等量关系,可得方程.
【解析】解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
×2=,
故选:A.
【点睛】此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,找出题目中的等量关系.
8.(2025 临夏州一模)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=2,BN=4,则BD的长为( )
A. B. C. D.
【点拨】依据题意,连接BM,记BD与MN交于点O,先证△DMO≌△BNO,从而得DM=BN=4,再由线段MN垂直平分BD从而BM=DM=2,又在Rt△BAM中可得AM的值,从而再在Rt△BAD中可求得BD.
【解析】解:由题意,连接BM,记BD与MN交于点O,
∵线段MN垂直平分BD,
∴BO=DO,BM=DM.
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠MDO=∠NBO.
又∠DOM=∠BON,
∴△DMO≌△BNO.
∴DM=BN=BM=4.
在Rt△BAM中,
∴.
∴在Rt△BAD中可得,.
故选:C.
【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质和线段垂直平分线的性质,灵活运用各知识点是解答本题的关键.
9.(2025 浙江一模)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,且x3<x2<x1,下列正确的选项是( )
A.若y3<y1<y2,则x1 x2 x3>0 B.若y2<y3<y1,则x1 x2 x3<0
C.若y2<y1<y3,则x1 x2 x3>0 D.若y1<y3<y2,则x1 x2 x3>0
【点拨】根据x3<x2<x1,利用反比例函数的性质即可判断.
【解析】解:A、∵x3<x2<x1,
若y3<y1<y2,则k>0,
则x3<0,0<x2<x1,
故x1 x2 x3<0,本选项不正确;
B、∵x3<x2<x1,
若y2<y3<y1,则k>0,
则x3<x2<0,x1>0,
故x1 x2 x3>0,本选项不正确;
C、∵x3<x2<x1,
若y2<y1<y3,则k<0,
则x3<0,0<x2<x1,
故x1 x2 x3<0,本选项不正确;
D、∵x3<x2<x1,
若y1<y3<y2,则k<0,
则x3<x2<0,x1>0,
故x1 x2 x3>0,本选项正确;
故选:D.
【点睛】本题考查反比例函数图象上点的坐标特征,解题的关键是掌握反比例函数的性质,属于中考常考题型.
10.(2025 德阳模拟)如图,在正方形ABCD中,点E、F分别在AB、BC上,连接AF,过点E作EG⊥AF交CD于点G,连接FG.若AE=2BF,∠BAF=α,则∠EGF一定等于( )
A.45°+α B.45°﹣α C.2α D.α
【点拨】过点D作DH∥EG交AB于点H,连接AG,证明△ABF和△DAH全等得AH=BF,AF=DH,再根据AE=2BF得AH=HE=BF,再证明四边形DGEH是平行四边形得HE=DG=AH,进而再证明△AHD和△DGA全等得∠ADH=∠DAG=α,DH=AG,则∠FAG=90°﹣2α,AF=DH=AG,进而得∠AFG=∠AGF=45°+α,根据EG⊥AF得∠AGE=90°﹣∠FAG=2α,然后根据∠EGF=∠AGF﹣∠AGE即可得出答案.
【解析】解:过点D作DH∥EG交AB于点H,连接AG,如图所示:
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠CDA=90°,AB∥CD,
∴∠BAF+∠FAD=90°,
∵EG⊥AF,DH∥EG,
DH⊥AF,
∴∠ADH+∠FAD=90°,
∴∠BAF=∠ADH=α,
在△ABF和△DAH中,
,
∴△ABF≌△DAH(ASA),
∴AH=BF,AF=DH,
∴AE=AH+HE=BF+HE,
∵AE=2BF,
∴BF+HE=2BF,
∴HE=BF,
∴AH=HE=BF,
∵AB∥CD,DH∥EG,
∴四边形DGEH是平行四边形,
∴HE=DG,
∴AH=DG,
在△AHD和△DGA中,
,
∴△AHD≌△DGA(SAS),
∴∠ADH=∠DAG=α,DH=AG,
∴∠FAG=∠BAD﹣(∠BAF+∠DAG)=90°﹣2α,
∵AF=DH,DH=AG,
∴AF=AG,
∴∠AFG=∠AGF=(180°﹣∠FAG)=45°+α,
∵EG⊥AF,
∴∠AGE=90°﹣∠FAG=90°﹣(90°﹣2α)=2α,
∴∠EGF=∠AGF﹣∠AGE=45°+α﹣2α=45°﹣α.
故选:B.
【点睛】此题主要考查了正方形的性质,全等三角形的判定与性质,理解 正方形的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2025 楚雄州一模)分解因式:m2﹣9m= m(m﹣9) .
【点拨】直接提取公因式m即可.
【解析】解:原式=m(m﹣9).
故答案为:m(m﹣9).
【点睛】此题主要考查了提公因式法分解因式,关键是正确找出公因式.
12.(2025 新郑市模拟)方程组的解为 .
【点拨】利用加减消元法求解即可.
【解析】解:,
由①×3﹣②得,8x=8,解得x=1,
把x=1代入①中得3×1+y=5,解得y=2,
故原方程组的解是,
故答案为:.
【点睛】本题主要考查了二元一次方程组的解法,解二元一次方程组的常用解法:代入消元法和加减消元法,观察题目选择合适的方法是解题关键.
13.(2025 余姚市一模)某校运会百米预赛用抽签方式确定赛道,8条赛道的编号分别为1到8.若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:∵8条赛道的编号分别为1到8,
∴若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是,
故答案为:.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
14.(2025 衢州一模)如图,直线BC与⊙O相切于点C,点A在⊙O上,AB⊥BC于点B.若AB=3,BC=6,则⊙O的半径为 cm.
【点拨】连接OC、OA,过点A作AD⊥OC于D,根据切线的性质得到OC⊥BC,根据矩形的性质得到CD=AB=3,AD=BC=6,根据勾股定理计算即可.
【解析】解:如图,连接OC、OA,过点A作AD⊥OC于D,
∵直线BC与⊙O相切于点C,
∴OC⊥BC,
∵AB⊥BC,AD⊥OC,
∴四边形ABCD为矩形,
∴CD=AB=3,AD=BC=6,
设⊙O的半径为x,则OD=x﹣3,
在Rt△OAD中,OA2=AD2+OD2,即x2=62+(x﹣3)2,
解得:x=,
∴⊙O的半径为cm,
故答案为:.
【点睛】本题考查的是切线的性质,熟记圆的切线垂直于经过切点的半径是解题的关键.
15.(2025 苏州一模)二次函数y=ax2+bx+c(其中a,b,c为常数,且a≠0)的图象以点A(1,m),B(3,m),C(0,﹣m),其中m为常数,且m≠0,则方程ax2+bx﹣2c=0的解为 2 .
【点拨】列出方程组求出a、b、c的值,则方程ax2+bx﹣2c=0为﹣mx2++2m=0,即可求解.
【解析】解:由题意得:,
解得:,
则方程ax2+bx﹣2c=0为﹣mx2++2m=0,
解得:x=2,
故答案为:2.
【点睛】本题考查了待定系数法求二次函数解析式,掌握方程组的求解是解题的关键.
16.(2025 温州一模)如图,点E,F分别在 ABCD的边AB,CD上,连结DE,EF,点D关于EF的对称点G恰好在AB的延长线上,连结FG交BC于点H.若,CF=1,则= ,AE= .
【点拨】连接DG,由平行四边形的性质得AD∥BC,AB∥CD,则∠AED=∠EDF,由轴对称的性质得EF垂直平分DG,∠EGF=∠EDF,则∠EGF=∠AED,所以FG∥ED,可证明四边形DEGF是菱形,则EG=FG,由=,得GH=EG=FG,=,求得FH=FG,则=,再证明△CFH∽△BGH,得==,求得BG=CF=,再证明△BGH∽△AED,得==,求得AE=BG=,于是得到问题的答案.
【解析】解:连接DG,
∵四边形ABCD是平行四边形,E,F分别在边AB,CD上,
∴AD∥BC,AB∥CD,
∴∠AED=∠EDF,
∵点D关于EF的对称点G恰好在AB的延长线上,FG交BC于点H,
∴EF垂直平分DG,EG∥FD,∠BGH=∠FDE,∠GBH=∠A,
∴EG=ED,FG=FD,
∵EF=EF,
∴△GEF≌△DEF(SSS),
∴∠EGF=∠EDF,
∴∠EGF=∠AED,
∴FG∥ED,
∴四边形DEGF是平行四边形,
∵EG=ED,
∴四边形DEGF是菱形,
∴EG=FG,
∵=,
∴GH=EG=FG,=,
∴FH=FG﹣FG=FG,
∴==,
∵CF∥BG,CF=1,
∴△CFH∽△BGH,
∴==,
∴BG=CF=,
∵∠BGH=∠AED,∠GBH=∠A,
∴△BGH∽△AED,
∴==,
∴AE=BG=×=,
故答案为:,.
【点睛】此题重点考查平行四边形的性质、轴对称的秘技、菱形的判定与性质、相似三角形的判定与性质等知识,证明四边形DEGF是菱形是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(2025 襄州区二模)计算:.
【点拨】利用绝对值的性质,算术平方根的定义,负整数指数幂计算后再算乘法,最后算加减即可.
【解析】解:原式=
=﹣2.
【点睛】本题考查实数的运算,负整数指数幂,熟练掌握相关运算法则是解题的关键.
18.(2025 扬州模拟)解不等式组:,并在数轴上表示解集.
【点拨】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解析】解:,
由①得:x<,
由②得:x≤1,
∴不等式组的解集为x≤1.
在数轴上表示为:.
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
19.(2024 普陀区二模)如图,在△ABC中,∠B=2∠C,点D在边BC上,AB=AD=13,BC=23.
(1)求BD的长;
(2)求tanC的值.
【点拨】(1)利用外角定理,结合等角对等边即可解决问题.
(2)过点A作BC的垂线构造出直角三角形即可解决问题.
【解析】解:(1)∵AB=AD,
∴∠B=∠ADB,
又∵∠B=2∠C,
∴∠ADB=2∠C.
又∵∠ADB=∠C+∠CAD,
∴∠C=∠CAD,
∴AD=CD.
∵AB=AD=13,BC=23,
∴BD=23﹣13=10.
(2)过点A作BC的垂线,垂足为M,
∵AB=AD,
∴BM=DM=,
∴CM=13+5=18.
在Rt△AMD中,
AM=,
∴tanC==.
【点睛】本题考查解直角三角形,过点A作BC的垂线构造出直角三角形是解题的关键.
20.(2025 西和县模拟)为弘扬向善、为善的优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,九年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 50 ,并补全条形统计图;
(2)本次捐款金额的众数为 15 元,中位数为 15 元;
(3)若该校九年级学生为600名,请你估算捐款金额为20元及以上的学生人数.
【点拨】(1)从两个统计图中可知,样本中“捐款为5元”的学生有8人,占调查人数的16%,根据频率=可求出答案;
(2)根据众数、中位数的定义进行计算即可;
(3)求出样本平均数,估计总体平均数,再进行计算即可.
【解析】解:(1)解:8÷16%=50(人),
“捐款为15元”的学生有50﹣8﹣14﹣6﹣4=18(人),
补全条形统计图如下:
故答案为:50;
(2)将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数==15(元),
这50名学生捐款人数最多的是15元,因此众数是15元.
故答案为:15,15;
(3)全校九年级学生为600名,估算捐款金额为20元及以上的学生人数为600×=120(名),
答:估算捐款金额为20元及以上的学生人数为120名.
【点睛】本题考查扇形统计图,条形统计图,中位数、众数以及样本估计总体,理解两个统计图中数量之间的关系,掌握中位数、众数的计算方法是正确解答的前提.
21.(2025 大庆一模)如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证EO=OF;
(2)若FC=2,求矩形ABCD的面积.
【点拨】(1)由AAS可证△AOE △COF,可得EO=OF;
(2)由直角三角形的性质可得CF=AE=2,BC=2,BF=2CF=4,即可求解.
【解析】(1)证明:∵AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
,
∴△AOE △COF(AAS),
∴EO=OF;
(2)解:如图,连接OB.
∵BE=BF,OE=OF,
∴BO⊥EF.
∴∠BEF+∠ABO=90°,
∵OA=OB,
∴∠BAC=∠ABO,
又∠BEF=2∠BAC,
∴2∠BAC+∠BAC=90°.
∴∠BAC=30°,∠BEO=60°,
∴△EBF是等边三角形,
∴∠EBF=60°,EB=BF,
∴∠CBF=30°,
∵CF=2,
∴CF=AE=2,BC=2,BF=2CF=4,
∴BF=BE=4,
∴AB=AE+BE=6,
∴矩形ABCD的面积=.
【点睛】本题考查了矩形的性质,全等三角形的判定和性质,等边三角形的判定和性质,灵活运用这些性质解决问题是解题的关键.
22.(2025 佳木斯一模)小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(单位:km)与小王的行驶时间t(单位:h)之间的函数关系的图象,请结合图象回答下列问题:
(1)求CD所在直线的函数表达式;
(2)求点K的坐标;
(3)请直接写出小王行驶多长时间时和妈妈相距4km.
【点拨】(1)利用待定系数法解答即可;
(2)写出OA所在直线的函数表达式,与CD所在直线的函数表达式联立建立关于x和y的二元一次方程组并求解,从而得到点K的坐标;
(3)按照t的不同的取值列关于t的方程并求解即可.
【解析】解:(1)设CD所在直线的函数表达式为y=kt+b(k、b为常数,且k≠0),
将坐标C(0.1,8)和D(0.5,0)分别代入y=kt+b,
得,
解得,
∴CD所在直线的函数表达式为y=﹣20t+10(0.1≤t≤0.5).
(2)小王的速度为8÷0.8=10(km/h),
∴OA所在直线的函数表达式为y=10t(0≤t≤0.8),
,
解得,
∴点K的坐标为(,).
(3)当0≤t≤0.1时,当二人相距4km时,得8﹣10t=4,
解得t=0.4(舍去),
当0.1<t≤0.5时,当二人相距4km时,得|﹣20t+10﹣10t|=4,
解得t=或.
答:小王行驶h或h和妈妈相距4km.
【点睛】本题考查一次函数的应用,掌握待定系数法求一次函数的关系式及速度、时间和路程之间的关系是解题的关键.
23.(2024 海淀区一模)在平面直角坐标系xOy中,点(m,n)在抛物线y=ax2+bx(a>0)上,其中m≠0.
(1)当m=4,n=0时.求抛物线的对称轴;
(2)已知当0<m<4时,总有n<0.
①求证:4a+b≤0;
②点P(k,y1),Q(3k,y2)在该抛物线上,是否存在a,b,使得当1<k<2时,都有y1<y2?若存在,求出a与b之间的数量关系;若不存在.说明理由.
【点拨】(1)理由待定系数法求得a,b的关系式,再利用利用二次函数的性质解答即可;
(2)①令y=0,则ax2+bx=0,得到抛物线y=ax2+bx(a>0)与x轴交于点(0,0),,利用分类讨论的思想方法分b>0,和b<0两种情况利用二次函数的性质讨论解答即可;
②利用分类讨论的思想方法,利用二次函数的图象的性质讨论解答即可.
【解析】(1)解:由题意可知:点(m,n)在抛物线y=ax2+bx(a>0)上,m=4,n=0
∴16a+4b=0,
∴b=﹣4a,
∴x=,
∴抛物线的对称轴为直线x=2;
(2)①证明:令y=0,则ax2+bx=0(a>0),
解得:x=0或 ,
∴抛物线y=ax2+bx(a>0)与x轴交于点(0,0),,
∵a>0,
∴抛物线开口向上,
(Ⅰ)当b<0时,
∵,
∴当0<x<﹣时,y<0;当x<0或时,y>0,
∵当0<m<4时,总有n<0,
∴.
∵a>0,
∴4a+b≤0,
(Ⅱ)当b>0时,
∵,
∴当时,y<0;当 或x>0时,y>0,
∴当0<m<4时,n>0,不符合题意,
综上,4a+b≤0;
②解:存在a,b,使得当1<k<2时,都有y1<y2,理由:
抛物线的对称轴为直线x=t=﹣,
由①知:.
∴﹣≥2,即t≥2.
∵a>0,
∴当x≥t时,y随x的增大而增大;当x≤t时,y随x的增大而减小.
∵1<k<2,
∴3<3k<6,k<3k,
(Ⅰ)当t=2时,
∵k<t<3k,此时P,Q均在对称轴的两侧,
∵y1<y2,
∴4﹣k<3k,
∴k>1,恒成立;
∴当t=2时,符合题意;
∴﹣=2,
∴4a+b=0.
(Ⅱ)当2<t≤3时,
令,
∴,则y1=y2,不符合题意,
(Ⅲ)当3<t<6时,
令3k=t,则k<3k≤t,
∴y1>y2,不符合题意;
(Ⅳ)当t≥6时,
∵k<3k<t,
∴y1>y2,不符合题意,
综上,4a+b=0.
综上,存在a,b,使得当1<k<2时,都有y1<y2,a与b之间的数量关系为:4a+b=0.
【点睛】本题主要考查了二次函数的图象与性质,待定系数法,不等式的性质,分类讨论的思想方法,熟练掌握二次函数的性质和利用分类讨论的方法解答是解题的关键.
24.(2025 蚌埠模拟)如图1,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连结CD,CA,AD.
(1)求证:OC平分∠ACD.
(2)如图2,延长AC,DB相交于点E.
①求证:OC∥BE.
②若,BD=6,求⊙O的半径.
【点拨】(1)由点C为的中点,得=,所以AC=DC,由垂径定理得OC⊥AD,即可根据等腰三角形的“三线合一”证明OC平分∠ACD;
(2)由AB是⊙O的直径,得∠ADB=90°,由OC⊥AD,BE⊥AD,得OC∥BE;
②连结BC,则∠ACB=90°,由OC=OA,∠OAC=∠OCA,由平行线的性质得∠OCA=∠E,则∠OAC=∠E,所以EB=AB,而BC⊥AE,则CA=CE=4,所以AE=8,设⊙O的半径为r,则EB=AB=2r,DE=6+2r,由勾股定理得(2r)2﹣62=(8)2﹣(6+2r)2=AD2,求出符合题意的r值即可.
【解析】(1)证明:∵点C为的中点,
∴=,
∴AC=DC,OC⊥AD,
∴OC平分∠ACD.
(2)①证明:
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BE⊥AD,
∵OC⊥AD,BE⊥AD,
∴OC∥BE.
②解:如图2,连结BC,则∠ACB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∵OC∥BE,
∴∠OCA=∠E,
∴∠OAC=∠E,
∴EB=AB,
∵BC⊥AE,
∴CA=CE=4,
∴AE=2CE=8,
设⊙O的半径为r,则EB=AB=2r,
∵BD=6,
∴DE=BD+EB=6+2r,
∵AB2﹣BD2=AE2﹣DE2=AD2,
∴(2r)2﹣62=(8)2﹣(6+2r)2,
整理得r2+3r﹣40=0,
解得r1=5,r2=﹣8(不符合题意,舍去),
∴⊙O的半径长为5.
【点睛】此题重点考查垂径定理、直径所对的圆周角是直角、等腰三角形的判定、平行线的判定与性质、等腰三角形的“三线合一”、勾股定理、一元二次方程的解法等知识与方法,此题综合性强,难度较大,属于考试压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年浙江省中考数学模拟试卷(4)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 厦门模拟)用数轴上的点表示下列各数,其中与原点距离最远的点表示的数是( )
A.0 B.1 C.2 D.﹣3
2.(2025 尉氏县一模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B. C. D.
3.(2025 泰安模拟)ChatGPT是人工智能研究实验室OpenAI新推出的一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A.1.75×103 B.1.75×1012 C.1750×108 D.1.75×1011
4.(2025 亳州二模)下列运算正确的是( )
A.a2 a3=a6 B.(ab)2=ab2 C.(a3)2=a5 D.a7÷a3=a4
5.(2025 成都模拟)为响应习近平总书记强调的“着眼满足人民群众多样化、多层次、多方面的精神文化需求”这一号召,某市夜校开设漆扇制作课程,一周内每天报名的人数分别为:72,86,67,59,91,82,94,则这组数据的中位数是( )
A.59 B.67 C.82 D.86
6.(2025 浙江模拟)如图,若△ABC与△A'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
7.(2025 宿城区一模)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B. C. D.
8.(2025 临夏州一模)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=2,BN=4,则BD的长为( )
A. B. C. D.
9.(2025 浙江一模)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,且x3<x2<x1,下列正确的选项是( )
A.若y3<y1<y2,则x1 x2 x3>0 B.若y2<y3<y1,则x1 x2 x3<0
C.若y2<y1<y3,则x1 x2 x3>0 D.若y1<y3<y2,则x1 x2 x3>0
10.(2025 德阳模拟)如图,在正方形ABCD中,点E、F分别在AB、BC上,连接AF,过点E作EG⊥AF交CD于点G,连接FG.若AE=2BF,∠BAF=α,则∠EGF一定等于( )
A.45°+α B.45°﹣α C.2α D.α
二、填空题:本题共6小题,每小题3分,共18分。
11.(2025 楚雄州一模)分解因式:m2﹣9m= .
12.(2025 新郑市模拟)方程组的解为 .
13.(2025 余姚市一模)某校运会百米预赛用抽签方式确定赛道,8条赛道的编号分别为1到8.若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是 .
14.(2025 衢州一模)如图,直线BC与⊙O相切于点C,点A在⊙O上,AB⊥BC于点B.若AB=3,BC=6,则⊙O的半径为 cm.
15.(2025 苏州一模)二次函数y=ax2+bx+c(其中a,b,c为常数,且a≠0)的图象以点A(1,m),B(3,m),C(0,﹣m),其中m为常数,且m≠0,则方程ax2+bx﹣2c=0的解为 .
16.(2025 温州一模)如图,点E,F分别在 ABCD的边AB,CD上,连结DE,EF,点D关于EF的对称点G恰好在AB的延长线上,连结FG交BC于点H.若,CF=1,则= ,AE= .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(2025 襄州区二模)计算:.
18.(2025 扬州模拟)解不等式组:,并在数轴上表示解集.
19.(2024 普陀区二模)如图,在△ABC中,∠B=2∠C,点D在边BC上,AB=AD=13,BC=23.
(1)求BD的长;
(2)求tanC的值.
20.(2025 西和县模拟)为弘扬向善、为善的优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,九年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 ,并补全条形统计图;
(2)本次捐款金额的众数为 元,中位数为 元;
(3)若该校九年级学生为600名,请你估算捐款金额为20元及以上的学生人数.
21.(2025 大庆一模)如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证EO=OF;
(2)若FC=2,求矩形ABCD的面积.
22.(2025 佳木斯一模)小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(单位:km)与小王的行驶时间t(单位:h)之间的函数关系的图象,请结合图象回答下列问题:
(1)求CD所在直线的函数表达式;
(2)求点K的坐标;
(3)请直接写出小王行驶多长时间时和妈妈相距4km.
23.(2024 海淀区一模)在平面直角坐标系xOy中,点(m,n)在抛物线y=ax2+bx(a>0)上,其中m≠0.
(1)当m=4,n=0时.求抛物线的对称轴;
(2)已知当0<m<4时,总有n<0.
①求证:4a+b≤0;
②点P(k,y1),Q(3k,y2)在该抛物线上,是否存在a,b,使得当1<k<2时,都有y1<y2?若存在,求出a与b之间的数量关系;若不存在.说明理由.
24.(2025 蚌埠模拟)如图1,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连结CD,CA,AD.
(1)求证:OC平分∠ACD.
(2)如图2,延长AC,DB相交于点E.
①求证:OC∥BE.
②若,BD=6,求⊙O的半径.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2025 厦门模拟)用数轴上的点表示下列各数,其中与原点距离最远的点表示的数是( )
A.0 B.1 C.2 D.﹣3
【点拨】到原点距离最远的点,即绝对值最大的点,首先求出各个数的绝对值,即可作出判断.
【解析】解:∵0、1、2、﹣3四个点所表示的有理数的绝对值分别为0、1、2、3,其中绝对值最大的是﹣3,
∴与原点距离最远的点表示的数是﹣3.
故选:D.
【点睛】本题考查了数轴,解题的关键是掌握数轴知识.
2.(2025 尉氏县一模)“斗”是我国古代称量粮食的量器,它无盖,其示意图如图所示,下列图形是“斗”的俯视图的是( )
A. B. C. D.
【点拨】根据俯视图是从上面看到的图形进行求解即可.
【解析】解:从上面看,看到的图形为一个正方形,在这个正方形里面还有一个小正方形,即看到的图形为,
故选C.
【点睛】本题主要考查了简单几何体的三视图,熟知俯视图是从上面看到的图形是解题的关键.
3.(2025 泰安模拟)ChatGPT是人工智能研究实验室OpenAI新推出的一种由人工智能技术驱动的自然语言处理工具,其技术底座有着多达175000000000个模型参数,数据175000000000用科学记数法表示为( )
A.1.75×103 B.1.75×1012 C.1750×108 D.1.75×1011
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:175000000000=1.75×1011.
故选:D.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2025 亳州二模)下列运算正确的是( )
A.a2 a3=a6 B.(ab)2=ab2 C.(a3)2=a5 D.a7÷a3=a4
【点拨】根据同底数幂相乘,底数不变,指数相加;积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;幂的乘方,底数不变,指数相乘;同底数幂相除,底数不变,指数相减;对各选项分析判断后利用排除法求解.
【解析】解:A、a2 a3=a5,故此选项不符合题意;
B、(ab)2=a2b2,故此选项不符合题意;
C、(a3)2=a6,故此选项不符合题意;
D、a7÷a3=a4,故此选项符合题意;
故选:D.
【点睛】本题考查了同底数幂的乘法、幂的乘方与积的乘方、同底数幂的除法,熟练掌握运算法则是解题的关键.
5.(2025 成都模拟)为响应习近平总书记强调的“着眼满足人民群众多样化、多层次、多方面的精神文化需求”这一号召,某市夜校开设漆扇制作课程,一周内每天报名的人数分别为:72,86,67,59,91,82,94,则这组数据的中位数是( )
A.59 B.67 C.82 D.86
【点拨】利用中位数的定义求解即可.
【解析】解:将数据按照从小到大的顺序排列:59,67,72,82,86,91,94,
一共有7个数,处在中间位置的数是82,
∴这组数据的中位数是82.
故选:C.
【点睛】本题主要考查了中位数的概念,正确理解中位数的概念是解题的关键.
6.(2025 浙江模拟)如图,若△ABC与△A'B'C'是位似图形,则位似中心的坐标为( )
A.(1,﹣1) B.(1,1) C.(2,0) D.(0,﹣1)
【点拨】根据位似的两个图形对应点的连线都经过同一点解答.
【解析】解:延长A′A、B′B交于点P,
则点P(1,﹣1)为位似中心,
故选:A.
【点睛】本题考查的是位似变换的概念,掌握位似的两个图形是相似形、对应点的连线都经过同一点是解题的关键.
7.(2025 宿城区一模)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B. C. D.
【点拨】首先设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得等量关系:慢马速度×2=快马速度,根据等量关系,可得方程.
【解析】解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
×2=,
故选:A.
【点睛】此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,找出题目中的等量关系.
8.(2025 临夏州一模)如图,矩形ABCD中,对角线BD的垂直平分线MN分别交AD,BC于点M,N.若AM=2,BN=4,则BD的长为( )
A. B. C. D.
【点拨】依据题意,连接BM,记BD与MN交于点O,先证△DMO≌△BNO,从而得DM=BN=4,再由线段MN垂直平分BD从而BM=DM=2,又在Rt△BAM中可得AM的值,从而再在Rt△BAD中可求得BD.
【解析】解:由题意,连接BM,记BD与MN交于点O,
∵线段MN垂直平分BD,
∴BO=DO,BM=DM.
∵四边形ABCD是矩形,
∴AD∥BC.
∴∠MDO=∠NBO.
又∠DOM=∠BON,
∴△DMO≌△BNO.
∴DM=BN=BM=4.
在Rt△BAM中,
∴.
∴在Rt△BAD中可得,.
故选:C.
【点睛】本题主要考查了矩形的性质、全等三角形的判定与性质和线段垂直平分线的性质,灵活运用各知识点是解答本题的关键.
9.(2025 浙江一模)已知点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数的图象上,且x3<x2<x1,下列正确的选项是( )
A.若y3<y1<y2,则x1 x2 x3>0 B.若y2<y3<y1,则x1 x2 x3<0
C.若y2<y1<y3,则x1 x2 x3>0 D.若y1<y3<y2,则x1 x2 x3>0
【点拨】根据x3<x2<x1,利用反比例函数的性质即可判断.
【解析】解:A、∵x3<x2<x1,
若y3<y1<y2,则k>0,
则x3<0,0<x2<x1,
故x1 x2 x3<0,本选项不正确;
B、∵x3<x2<x1,
若y2<y3<y1,则k>0,
则x3<x2<0,x1>0,
故x1 x2 x3>0,本选项不正确;
C、∵x3<x2<x1,
若y2<y1<y3,则k<0,
则x3<0,0<x2<x1,
故x1 x2 x3<0,本选项不正确;
D、∵x3<x2<x1,
若y1<y3<y2,则k<0,
则x3<x2<0,x1>0,
故x1 x2 x3>0,本选项正确;
故选:D.
【点睛】本题考查反比例函数图象上点的坐标特征,解题的关键是掌握反比例函数的性质,属于中考常考题型.
10.(2025 德阳模拟)如图,在正方形ABCD中,点E、F分别在AB、BC上,连接AF,过点E作EG⊥AF交CD于点G,连接FG.若AE=2BF,∠BAF=α,则∠EGF一定等于( )
A.45°+α B.45°﹣α C.2α D.α
【点拨】过点D作DH∥EG交AB于点H,连接AG,证明△ABF和△DAH全等得AH=BF,AF=DH,再根据AE=2BF得AH=HE=BF,再证明四边形DGEH是平行四边形得HE=DG=AH,进而再证明△AHD和△DGA全等得∠ADH=∠DAG=α,DH=AG,则∠FAG=90°﹣2α,AF=DH=AG,进而得∠AFG=∠AGF=45°+α,根据EG⊥AF得∠AGE=90°﹣∠FAG=2α,然后根据∠EGF=∠AGF﹣∠AGE即可得出答案.
【解析】解:过点D作DH∥EG交AB于点H,连接AG,如图所示:
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠CDA=90°,AB∥CD,
∴∠BAF+∠FAD=90°,
∵EG⊥AF,DH∥EG,
DH⊥AF,
∴∠ADH+∠FAD=90°,
∴∠BAF=∠ADH=α,
在△ABF和△DAH中,
,
∴△ABF≌△DAH(ASA),
∴AH=BF,AF=DH,
∴AE=AH+HE=BF+HE,
∵AE=2BF,
∴BF+HE=2BF,
∴HE=BF,
∴AH=HE=BF,
∵AB∥CD,DH∥EG,
∴四边形DGEH是平行四边形,
∴HE=DG,
∴AH=DG,
在△AHD和△DGA中,
,
∴△AHD≌△DGA(SAS),
∴∠ADH=∠DAG=α,DH=AG,
∴∠FAG=∠BAD﹣(∠BAF+∠DAG)=90°﹣2α,
∵AF=DH,DH=AG,
∴AF=AG,
∴∠AFG=∠AGF=(180°﹣∠FAG)=45°+α,
∵EG⊥AF,
∴∠AGE=90°﹣∠FAG=90°﹣(90°﹣2α)=2α,
∴∠EGF=∠AGF﹣∠AGE=45°+α﹣2α=45°﹣α.
故选:B.
【点睛】此题主要考查了正方形的性质,全等三角形的判定与性质,理解 正方形的性质,熟练掌握全等三角形的判定与性质是解决问题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.(2025 楚雄州一模)分解因式:m2﹣9m= m(m﹣9) .
【点拨】直接提取公因式m即可.
【解析】解:原式=m(m﹣9).
故答案为:m(m﹣9).
【点睛】此题主要考查了提公因式法分解因式,关键是正确找出公因式.
12.(2025 新郑市模拟)方程组的解为 .
【点拨】利用加减消元法求解即可.
【解析】解:,
由①×3﹣②得,8x=8,解得x=1,
把x=1代入①中得3×1+y=5,解得y=2,
故原方程组的解是,
故答案为:.
【点睛】本题主要考查了二元一次方程组的解法,解二元一次方程组的常用解法:代入消元法和加减消元法,观察题目选择合适的方法是解题关键.
13.(2025 余姚市一模)某校运会百米预赛用抽签方式确定赛道,8条赛道的编号分别为1到8.若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:∵8条赛道的编号分别为1到8,
∴若琪琪第一个抽签,她随机抽取一签,则抽到6号赛道的概率是,
故答案为:.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
14.(2025 衢州一模)如图,直线BC与⊙O相切于点C,点A在⊙O上,AB⊥BC于点B.若AB=3,BC=6,则⊙O的半径为 cm.
【点拨】连接OC、OA,过点A作AD⊥OC于D,根据切线的性质得到OC⊥BC,根据矩形的性质得到CD=AB=3,AD=BC=6,根据勾股定理计算即可.
【解析】解:如图,连接OC、OA,过点A作AD⊥OC于D,
∵直线BC与⊙O相切于点C,
∴OC⊥BC,
∵AB⊥BC,AD⊥OC,
∴四边形ABCD为矩形,
∴CD=AB=3,AD=BC=6,
设⊙O的半径为x,则OD=x﹣3,
在Rt△OAD中,OA2=AD2+OD2,即x2=62+(x﹣3)2,
解得:x=,
∴⊙O的半径为cm,
故答案为:.
【点睛】本题考查的是切线的性质,熟记圆的切线垂直于经过切点的半径是解题的关键.
15.(2025 苏州一模)二次函数y=ax2+bx+c(其中a,b,c为常数,且a≠0)的图象以点A(1,m),B(3,m),C(0,﹣m),其中m为常数,且m≠0,则方程ax2+bx﹣2c=0的解为 2 .
【点拨】列出方程组求出a、b、c的值,则方程ax2+bx﹣2c=0为﹣mx2++2m=0,即可求解.
【解析】解:由题意得:,
解得:,
则方程ax2+bx﹣2c=0为﹣mx2++2m=0,
解得:x=2,
故答案为:2.
【点睛】本题考查了待定系数法求二次函数解析式,掌握方程组的求解是解题的关键.
16.(2025 温州一模)如图,点E,F分别在 ABCD的边AB,CD上,连结DE,EF,点D关于EF的对称点G恰好在AB的延长线上,连结FG交BC于点H.若,CF=1,则= ,AE= .
【点拨】连接DG,由平行四边形的性质得AD∥BC,AB∥CD,则∠AED=∠EDF,由轴对称的性质得EF垂直平分DG,∠EGF=∠EDF,则∠EGF=∠AED,所以FG∥ED,可证明四边形DEGF是菱形,则EG=FG,由=,得GH=EG=FG,=,求得FH=FG,则=,再证明△CFH∽△BGH,得==,求得BG=CF=,再证明△BGH∽△AED,得==,求得AE=BG=,于是得到问题的答案.
【解析】解:连接DG,
∵四边形ABCD是平行四边形,E,F分别在边AB,CD上,
∴AD∥BC,AB∥CD,
∴∠AED=∠EDF,
∵点D关于EF的对称点G恰好在AB的延长线上,FG交BC于点H,
∴EF垂直平分DG,EG∥FD,∠BGH=∠FDE,∠GBH=∠A,
∴EG=ED,FG=FD,
∵EF=EF,
∴△GEF≌△DEF(SSS),
∴∠EGF=∠EDF,
∴∠EGF=∠AED,
∴FG∥ED,
∴四边形DEGF是平行四边形,
∵EG=ED,
∴四边形DEGF是菱形,
∴EG=FG,
∵=,
∴GH=EG=FG,=,
∴FH=FG﹣FG=FG,
∴==,
∵CF∥BG,CF=1,
∴△CFH∽△BGH,
∴==,
∴BG=CF=,
∵∠BGH=∠AED,∠GBH=∠A,
∴△BGH∽△AED,
∴==,
∴AE=BG=×=,
故答案为:,.
【点睛】此题重点考查平行四边形的性质、轴对称的秘技、菱形的判定与性质、相似三角形的判定与性质等知识,证明四边形DEGF是菱形是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.(2025 襄州区二模)计算:.
【点拨】利用绝对值的性质,算术平方根的定义,负整数指数幂计算后再算乘法,最后算加减即可.
【解析】解:原式=
=﹣2.
【点睛】本题考查实数的运算,负整数指数幂,熟练掌握相关运算法则是解题的关键.
18.(2025 扬州模拟)解不等式组:,并在数轴上表示解集.
【点拨】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.
【解析】解:,
由①得:x<,
由②得:x≤1,
∴不等式组的解集为x≤1.
在数轴上表示为:.
【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
19.(2024 普陀区二模)如图,在△ABC中,∠B=2∠C,点D在边BC上,AB=AD=13,BC=23.
(1)求BD的长;
(2)求tanC的值.
【点拨】(1)利用外角定理,结合等角对等边即可解决问题.
(2)过点A作BC的垂线构造出直角三角形即可解决问题.
【解析】解:(1)∵AB=AD,
∴∠B=∠ADB,
又∵∠B=2∠C,
∴∠ADB=2∠C.
又∵∠ADB=∠C+∠CAD,
∴∠C=∠CAD,
∴AD=CD.
∵AB=AD=13,BC=23,
∴BD=23﹣13=10.
(2)过点A作BC的垂线,垂足为M,
∵AB=AD,
∴BM=DM=,
∴CM=13+5=18.
在Rt△AMD中,
AM=,
∴tanC==.
【点睛】本题考查解直角三角形,过点A作BC的垂线构造出直角三角形是解题的关键.
20.(2025 西和县模拟)为弘扬向善、为善的优秀品质,助力爱心公益事业,某校组织开展“人间自有真情在,爱心助力暖人心”慈善捐款活动,九年级全体同学参加了此次活动.随机抽查了部分同学捐款的情况,统计结果如图1和图2所示.
(1)本次抽查的学生人数是 50 ,并补全条形统计图;
(2)本次捐款金额的众数为 15 元,中位数为 15 元;
(3)若该校九年级学生为600名,请你估算捐款金额为20元及以上的学生人数.
【点拨】(1)从两个统计图中可知,样本中“捐款为5元”的学生有8人,占调查人数的16%,根据频率=可求出答案;
(2)根据众数、中位数的定义进行计算即可;
(3)求出样本平均数,估计总体平均数,再进行计算即可.
【解析】解:(1)解:8÷16%=50(人),
“捐款为15元”的学生有50﹣8﹣14﹣6﹣4=18(人),
补全条形统计图如下:
故答案为:50;
(2)将这50名学生捐款金额从小到大排列处在中间位置的两个数都是15元,因此中位数==15(元),
这50名学生捐款人数最多的是15元,因此众数是15元.
故答案为:15,15;
(3)全校九年级学生为600名,估算捐款金额为20元及以上的学生人数为600×=120(名),
答:估算捐款金额为20元及以上的学生人数为120名.
【点睛】本题考查扇形统计图,条形统计图,中位数、众数以及样本估计总体,理解两个统计图中数量之间的关系,掌握中位数、众数的计算方法是正确解答的前提.
21.(2025 大庆一模)如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.
(1)求证EO=OF;
(2)若FC=2,求矩形ABCD的面积.
【点拨】(1)由AAS可证△AOE △COF,可得EO=OF;
(2)由直角三角形的性质可得CF=AE=2,BC=2,BF=2CF=4,即可求解.
【解析】(1)证明:∵AB∥CD,
∴∠BAC=∠FCO,
在△AOE和△COF中,
,
∴△AOE △COF(AAS),
∴EO=OF;
(2)解:如图,连接OB.
∵BE=BF,OE=OF,
∴BO⊥EF.
∴∠BEF+∠ABO=90°,
∵OA=OB,
∴∠BAC=∠ABO,
又∠BEF=2∠BAC,
∴2∠BAC+∠BAC=90°.
∴∠BAC=30°,∠BEO=60°,
∴△EBF是等边三角形,
∴∠EBF=60°,EB=BF,
∴∠CBF=30°,
∵CF=2,
∴CF=AE=2,BC=2,BF=2CF=4,
∴BF=BE=4,
∴AB=AE+BE=6,
∴矩形ABCD的面积=.
【点睛】本题考查了矩形的性质,全等三角形的判定和性质,等边三角形的判定和性质,灵活运用这些性质解决问题是解题的关键.
22.(2025 佳木斯一模)小王骑自行车从家出发沿公路匀速前往新华书店,小王妈妈骑电瓶车从新华书店出发沿同一条路回家,线段OA与折线B﹣C﹣D﹣E分别表示两人离家的距离y(单位:km)与小王的行驶时间t(单位:h)之间的函数关系的图象,请结合图象回答下列问题:
(1)求CD所在直线的函数表达式;
(2)求点K的坐标;
(3)请直接写出小王行驶多长时间时和妈妈相距4km.
【点拨】(1)利用待定系数法解答即可;
(2)写出OA所在直线的函数表达式,与CD所在直线的函数表达式联立建立关于x和y的二元一次方程组并求解,从而得到点K的坐标;
(3)按照t的不同的取值列关于t的方程并求解即可.
【解析】解:(1)设CD所在直线的函数表达式为y=kt+b(k、b为常数,且k≠0),
将坐标C(0.1,8)和D(0.5,0)分别代入y=kt+b,
得,
解得,
∴CD所在直线的函数表达式为y=﹣20t+10(0.1≤t≤0.5).
(2)小王的速度为8÷0.8=10(km/h),
∴OA所在直线的函数表达式为y=10t(0≤t≤0.8),
,
解得,
∴点K的坐标为(,).
(3)当0≤t≤0.1时,当二人相距4km时,得8﹣10t=4,
解得t=0.4(舍去),
当0.1<t≤0.5时,当二人相距4km时,得|﹣20t+10﹣10t|=4,
解得t=或.
答:小王行驶h或h和妈妈相距4km.
【点睛】本题考查一次函数的应用,掌握待定系数法求一次函数的关系式及速度、时间和路程之间的关系是解题的关键.
23.(2024 海淀区一模)在平面直角坐标系xOy中,点(m,n)在抛物线y=ax2+bx(a>0)上,其中m≠0.
(1)当m=4,n=0时.求抛物线的对称轴;
(2)已知当0<m<4时,总有n<0.
①求证:4a+b≤0;
②点P(k,y1),Q(3k,y2)在该抛物线上,是否存在a,b,使得当1<k<2时,都有y1<y2?若存在,求出a与b之间的数量关系;若不存在.说明理由.
【点拨】(1)理由待定系数法求得a,b的关系式,再利用利用二次函数的性质解答即可;
(2)①令y=0,则ax2+bx=0,得到抛物线y=ax2+bx(a>0)与x轴交于点(0,0),,利用分类讨论的思想方法分b>0,和b<0两种情况利用二次函数的性质讨论解答即可;
②利用分类讨论的思想方法,利用二次函数的图象的性质讨论解答即可.
【解析】(1)解:由题意可知:点(m,n)在抛物线y=ax2+bx(a>0)上,m=4,n=0
∴16a+4b=0,
∴b=﹣4a,
∴x=,
∴抛物线的对称轴为直线x=2;
(2)①证明:令y=0,则ax2+bx=0(a>0),
解得:x=0或 ,
∴抛物线y=ax2+bx(a>0)与x轴交于点(0,0),,
∵a>0,
∴抛物线开口向上,
(Ⅰ)当b<0时,
∵,
∴当0<x<﹣时,y<0;当x<0或时,y>0,
∵当0<m<4时,总有n<0,
∴.
∵a>0,
∴4a+b≤0,
(Ⅱ)当b>0时,
∵,
∴当时,y<0;当 或x>0时,y>0,
∴当0<m<4时,n>0,不符合题意,
综上,4a+b≤0;
②解:存在a,b,使得当1<k<2时,都有y1<y2,理由:
抛物线的对称轴为直线x=t=﹣,
由①知:.
∴﹣≥2,即t≥2.
∵a>0,
∴当x≥t时,y随x的增大而增大;当x≤t时,y随x的增大而减小.
∵1<k<2,
∴3<3k<6,k<3k,
(Ⅰ)当t=2时,
∵k<t<3k,此时P,Q均在对称轴的两侧,
∵y1<y2,
∴4﹣k<3k,
∴k>1,恒成立;
∴当t=2时,符合题意;
∴﹣=2,
∴4a+b=0.
(Ⅱ)当2<t≤3时,
令,
∴,则y1=y2,不符合题意,
(Ⅲ)当3<t<6时,
令3k=t,则k<3k≤t,
∴y1>y2,不符合题意;
(Ⅳ)当t≥6时,
∵k<3k<t,
∴y1>y2,不符合题意,
综上,4a+b=0.
综上,存在a,b,使得当1<k<2时,都有y1<y2,a与b之间的数量关系为:4a+b=0.
【点睛】本题主要考查了二次函数的图象与性质,待定系数法,不等式的性质,分类讨论的思想方法,熟练掌握二次函数的性质和利用分类讨论的方法解答是解题的关键.
24.(2025 蚌埠模拟)如图1,AB是⊙O的直径,点D为AB下方⊙O上一点,点C为的中点,连结CD,CA,AD.
(1)求证:OC平分∠ACD.
(2)如图2,延长AC,DB相交于点E.
①求证:OC∥BE.
②若,BD=6,求⊙O的半径.
【点拨】(1)由点C为的中点,得=,所以AC=DC,由垂径定理得OC⊥AD,即可根据等腰三角形的“三线合一”证明OC平分∠ACD;
(2)由AB是⊙O的直径,得∠ADB=90°,由OC⊥AD,BE⊥AD,得OC∥BE;
②连结BC,则∠ACB=90°,由OC=OA,∠OAC=∠OCA,由平行线的性质得∠OCA=∠E,则∠OAC=∠E,所以EB=AB,而BC⊥AE,则CA=CE=4,所以AE=8,设⊙O的半径为r,则EB=AB=2r,DE=6+2r,由勾股定理得(2r)2﹣62=(8)2﹣(6+2r)2=AD2,求出符合题意的r值即可.
【解析】(1)证明:∵点C为的中点,
∴=,
∴AC=DC,OC⊥AD,
∴OC平分∠ACD.
(2)①证明:
∵AB是⊙O的直径,
∴∠ADB=90°,
∴BE⊥AD,
∵OC⊥AD,BE⊥AD,
∴OC∥BE.
②解:如图2,连结BC,则∠ACB=90°,
∵OC=OA,
∴∠OAC=∠OCA,
∵OC∥BE,
∴∠OCA=∠E,
∴∠OAC=∠E,
∴EB=AB,
∵BC⊥AE,
∴CA=CE=4,
∴AE=2CE=8,
设⊙O的半径为r,则EB=AB=2r,
∵BD=6,
∴DE=BD+EB=6+2r,
∵AB2﹣BD2=AE2﹣DE2=AD2,
∴(2r)2﹣62=(8)2﹣(6+2r)2,
整理得r2+3r﹣40=0,
解得r1=5,r2=﹣8(不符合题意,舍去),
∴⊙O的半径长为5.
【点睛】此题重点考查垂径定理、直径所对的圆周角是直角、等腰三角形的判定、平行线的判定与性质、等腰三角形的“三线合一”、勾股定理、一元二次方程的解法等知识与方法,此题综合性强,难度较大,属于考试压轴题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
