2.2.1平行四边形的性质(1) 课件(共16张PPT)
文档属性
| 名称 | 2.2.1平行四边形的性质(1) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
2.2.1平行四边形的性质(1)
(湘教版)八年级
找一找:下列图片中,你发现了什么样的四边形?
情境导入
一
A
B
C
D
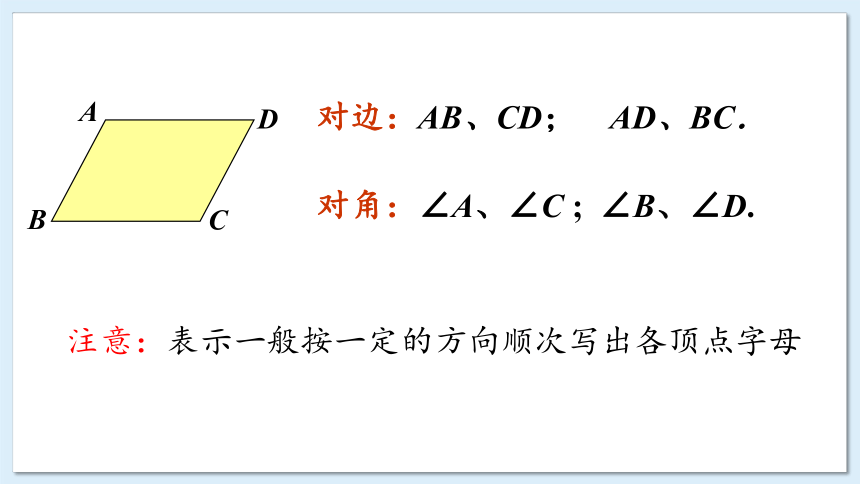
注意:表示一般按一定的方向顺次写出各顶点字母
对边:AB、CD; AD、BC.
对角:
∠A、∠C ; ∠B、∠D.
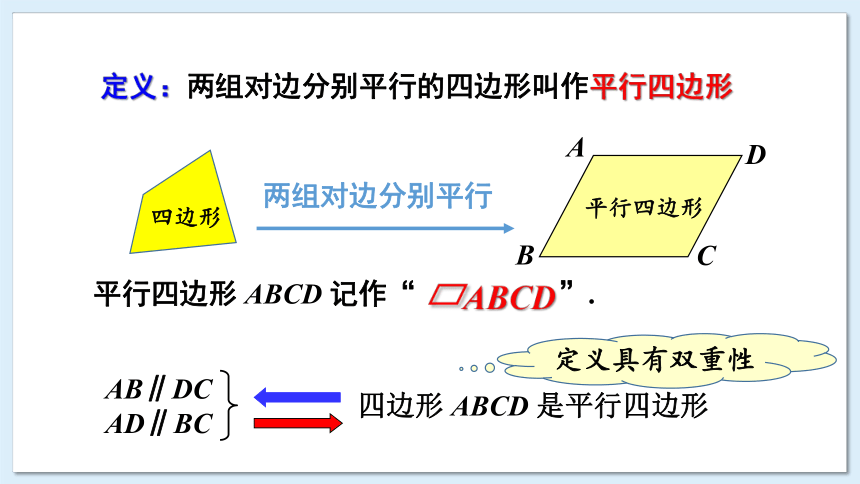
定义:两组对边分别平行的四边形叫作平行四边形
四边形
A
B
C
D
平行四边形
两组对边分别平行
平行四边形 ABCD 记作“ ”.
ABCD
四边形 ABCD 是平行四边形
AB∥DC
AD∥BC
定义具有双重性
由平行四边形的定义,我们知道平行四边形的两组对边分别平行.
想
想
一
平行四边形还有什么性质?
A
B
C
D
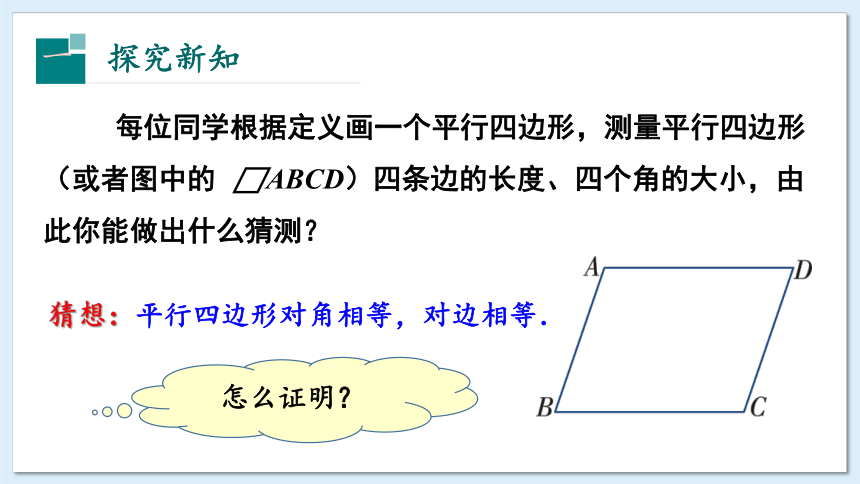
每位同学根据定义画一个平行四边形,测量平行四边形(或者图中的 ABCD)四条边的长度、四个角的大小,由此你能做出什么猜测?
猜想:平行四边形对角相等,对边相等.
怎么证明?
探究新知
一
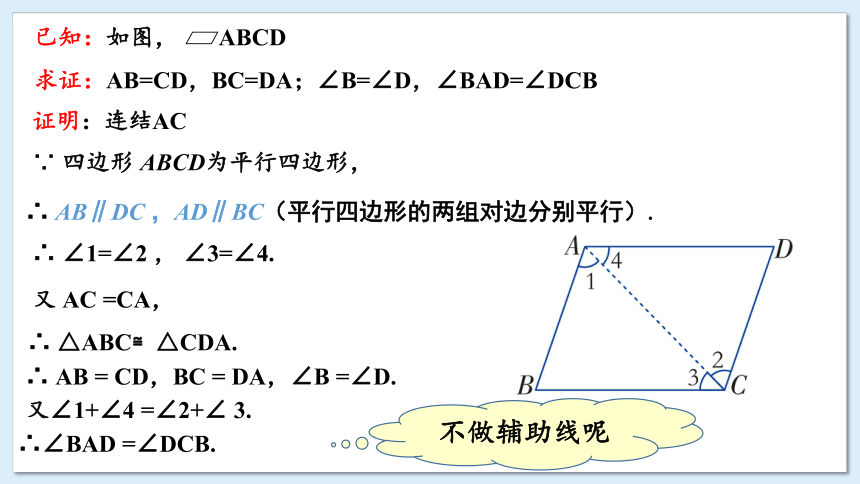
∴ ∠1=∠2 , ∠3=∠4.
∴ AB∥DC ,AD∥BC(平行四边形的两组对边分别平行).
∵ 四边形 ABCD为平行四边形,
又 AC =CA,
∴ AB = CD,BC = DA,∠B =∠D.
∴ △ABC≌△CDA.
又∠1+∠4 =∠2+∠ 3.
∴∠BAD =∠DCB.
已知:如图, ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
证明:连结AC
不做辅助线呢
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
A
B
C
D
符号 语言:
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A =∠C,∠B =∠D.
归纳小结
一
针对练习
一
如图,在 ABCD 中
(1)若∠A=130°,则∠B=_______ ,∠C=_____,∠D=______.
C
D
A
B
(2)若AB=3,BC=5,则它的周长= ______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
50°
130°
50°
16
100°
80°
如图,四边形 ABCD 和 BCEF 均为平行四边形,
AD = 2 cm,∠A = 65°,∠E = 33°,求 EF 和∠BGC.
【教材P41】
∵ 四边形 ABCD 是平行四边形
∴ AD = BC = 2 cm,∠1=∠A = 65°
∵ 四边形 BCEF是平行四边形
∴ EF = BC = 2 cm ,∠2 =∠E = 33°
∴ 在△BGC中,∠BGC = 180°-∠1 -∠2 = 82°
解:
例题解析
一
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
∴AB=CD.
∵l1∥l2,AB∥CD,
∴四边形ABDC是平行四边形.
解
夹在两条平行线间的平行线段相等.
【教材P41】
课堂小结
通过本节课的学习,你有什么收获?
定义
性质
两组对边分别平行的四边形叫作平行四边形.
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
拓展延伸
一
如图,△ABC是等腰三角形,P是底边BC上一动点,
且PE //AB,PF //AC,求证:PE+PF=AB.
C
A
B
E
F
P
当堂检测
一
1. 在 ABCD中,若∠B=70°,则∠D=( ).
(A)130° (B)110° (C)70° (D)35°
2. 在 ABCD中,若AB=2,BC=3,则AD=___________,CD=___________.
C
3
2
3. 如图 , 在□ ABCD 中, AE⊥BC 于点 E , AF⊥DC
交 DC 的延长线于点 F.若∠FCB = 30°, AE = 3,
AF=5, 求 □ ABCD 的周长.
解: 在□ ABCD 中, CD∥AB,
∴∠B = ∠FCB = 30°.
又∵AE⊥BC , ∴在 Rt△ABE 中, AB=2AE=6.
又∵ ∠B = ∠D , AF⊥DF ,
∴ 在Rt△AFD 中, AD = 2AF=10.
∴ □ ABCD 的周长为 2(AD+AB)=32.
2.2.1平行四边形的性质(1)
(湘教版)八年级
找一找:下列图片中,你发现了什么样的四边形?
情境导入
一
A
B
C
D
注意:表示一般按一定的方向顺次写出各顶点字母
对边:AB、CD; AD、BC.
对角:
∠A、∠C ; ∠B、∠D.
定义:两组对边分别平行的四边形叫作平行四边形
四边形
A
B
C
D
平行四边形
两组对边分别平行
平行四边形 ABCD 记作“ ”.
ABCD
四边形 ABCD 是平行四边形
AB∥DC
AD∥BC
定义具有双重性
由平行四边形的定义,我们知道平行四边形的两组对边分别平行.
想
想
一
平行四边形还有什么性质?
A
B
C
D
每位同学根据定义画一个平行四边形,测量平行四边形(或者图中的 ABCD)四条边的长度、四个角的大小,由此你能做出什么猜测?
猜想:平行四边形对角相等,对边相等.
怎么证明?
探究新知
一
∴ ∠1=∠2 , ∠3=∠4.
∴ AB∥DC ,AD∥BC(平行四边形的两组对边分别平行).
∵ 四边形 ABCD为平行四边形,
又 AC =CA,
∴ AB = CD,BC = DA,∠B =∠D.
∴ △ABC≌△CDA.
又∠1+∠4 =∠2+∠ 3.
∴∠BAD =∠DCB.
已知:如图, ABCD
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
证明:连结AC
不做辅助线呢
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
A
B
C
D
符号 语言:
∵四边形ABCD是平行四边形
∴AB=CD,AD=BC
∵四边形ABCD是平行四边形
∴∠A =∠C,∠B =∠D.
归纳小结
一
针对练习
一
如图,在 ABCD 中
(1)若∠A=130°,则∠B=_______ ,∠C=_____,∠D=______.
C
D
A
B
(2)若AB=3,BC=5,则它的周长= ______.
(3)若∠A+ ∠C= 200°,则∠A=_____,∠B=______.
50°
130°
50°
16
100°
80°
如图,四边形 ABCD 和 BCEF 均为平行四边形,
AD = 2 cm,∠A = 65°,∠E = 33°,求 EF 和∠BGC.
【教材P41】
∵ 四边形 ABCD 是平行四边形
∴ AD = BC = 2 cm,∠1=∠A = 65°
∵ 四边形 BCEF是平行四边形
∴ EF = BC = 2 cm ,∠2 =∠E = 33°
∴ 在△BGC中,∠BGC = 180°-∠1 -∠2 = 82°
解:
例题解析
一
如图,直线 l1 与 l2 平行,AB,CD是 l1 与 l2 之间的任意两条平行线段. 试问:AB与CD是否相等?为什么?
∴AB=CD.
∵l1∥l2,AB∥CD,
∴四边形ABDC是平行四边形.
解
夹在两条平行线间的平行线段相等.
【教材P41】
课堂小结
通过本节课的学习,你有什么收获?
定义
性质
两组对边分别平行的四边形叫作平行四边形.
平行四边形的两组对边分别相等.
平行四边形的两组对角分别相等.
拓展延伸
一
如图,△ABC是等腰三角形,P是底边BC上一动点,
且PE //AB,PF //AC,求证:PE+PF=AB.
C
A
B
E
F
P
当堂检测
一
1. 在 ABCD中,若∠B=70°,则∠D=( ).
(A)130° (B)110° (C)70° (D)35°
2. 在 ABCD中,若AB=2,BC=3,则AD=___________,CD=___________.
C
3
2
3. 如图 , 在□ ABCD 中, AE⊥BC 于点 E , AF⊥DC
交 DC 的延长线于点 F.若∠FCB = 30°, AE = 3,
AF=5, 求 □ ABCD 的周长.
解: 在□ ABCD 中, CD∥AB,
∴∠B = ∠FCB = 30°.
又∵AE⊥BC , ∴在 Rt△ABE 中, AB=2AE=6.
又∵ ∠B = ∠D , AF⊥DF ,
∴ 在Rt△AFD 中, AD = 2AF=10.
∴ □ ABCD 的周长为 2(AD+AB)=32.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
