2024--2025学年小学毕业会考数学人教版模拟试卷一
文档属性
| 名称 | 2024--2025学年小学毕业会考数学人教版模拟试卷一 |  | |
| 格式 | docx | ||
| 文件大小 | 549.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 17:45:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024--2025学年小学毕业会考数学人教版模拟试卷一
一、选择题
1.下面的描述中不符合日常生活常识的是( )。
A.六年级学生平均身高约145厘米 B.一枚鸡蛋重约60克
C.一瓶普通的牛奶大约250毫升 D.黄山市的总面积9807公顷
2.如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最小公倍数是( )。
A.a B.b C.c D.无法确定
3.小明误将错写成,结果与原式比较( )。
A.少5 B.少8 C.少32 D.和原来一样
4.下面不能用方程“”表示的是( )。
A. B.
C. D.
5.一个骰子六个面上分别有数字1,2,3,4,5,6,任意抛两次,上面的数字和是( )的可能性大。
A.6 B.7 C.8 D.9
6.一个盒子里有黄、白乒乓球各5个,要想使取出的乒乓球保证至少有2个白色的,则至少取出的个数是( )。
A.3 B.6 C.7 D.10
7.甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆的面积比是( )。
A.1∶8 B.4∶9 C.2∶3 D.3.14∶7.065
二、填空题
8.( )÷40==( )∶35==( )%。
9.我国某地一年中最高温度是42摄氏度,最低温度是﹣32摄氏度,最高温度与最低温度相差( )摄氏度。
10.比一比:1.303,,,,四个数中,最大的是( ),最小的是( )。
11.A和B互为倒数,且=,那么C=( )。
12.60m2比( )少20%,比80dm多的是( )dm。
13.把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长( ),小明拿的铁丝是这根铁丝的( )(填上合适的分数)。
14.去年收大豆3600kg,今年比去年减产二成,今年大豆减产( )kg。
15.用96朵康乃馨和72朵粉百合做成花束,每束花里的康乃馨朵数相同,粉百合朵数也相同,每束花里至少有( )朵花。
16.一种什锦糖是由酥糖、奶糖和水果糖按2∶3∶5混合配制而成的。如果这三种糖都有180千克,当奶糖全部用完时,酥糖还剩( )千克;水果糖则需要增加( )千克。
17.用一个底面直径是4cm,高为9cm的圆柱木块,削成一个最大的圆锥,圆锥的体积是( )cm3,削成最大圆锥的体积是削去木块体积的( )。
三、计算题
18.直接写出得数。
873+199= 0.64÷0.4= = 20×5÷20×5=
= = = =
19.脱式计算,能简算的要简算。
10.4÷[(0.64+1.44)×0.5]
20.解方程。
9×1.8-12x=1.8
21.如图,已知平行四边形的面积是100平方厘米。求阴影部分的面积。
四、作图题
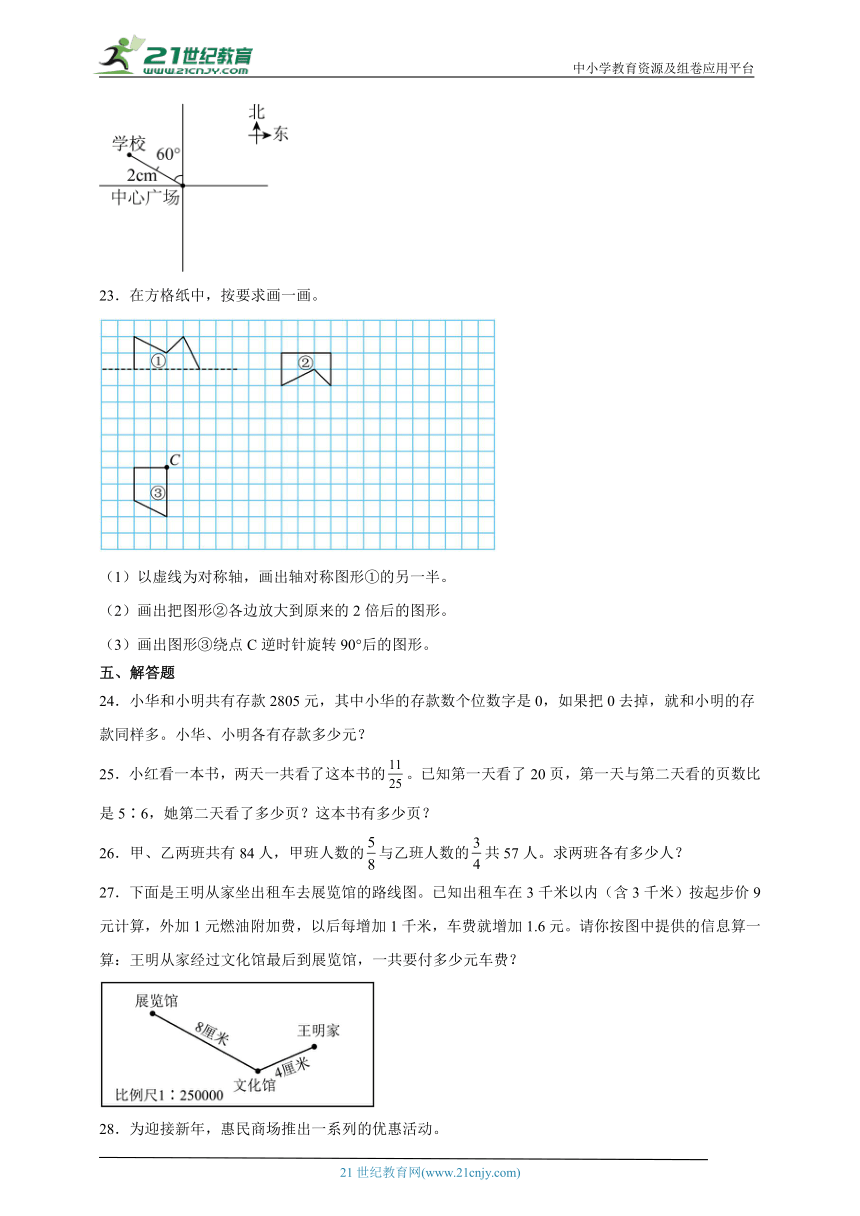
22.(1)学校在中心广场北偏西60°方向600米处,这幅图的比例尺是( )。
(2)书店在中心广场南偏东50°方向900米处,请在图中用“ ”标出书店的位置。
23.在方格纸中,按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出把图形②各边放大到原来的2倍后的图形。
(3)画出图形③绕点C逆时针旋转90°后的图形。
五、解答题
24.小华和小明共有存款2805元,其中小华的存款数个位数字是0,如果把0去掉,就和小明的存款同样多。小华、小明各有存款多少元?
25.小红看一本书,两天一共看了这本书的。已知第一天看了20页,第一天与第二天看的页数比是5∶6,她第二天看了多少页?这本书有多少页?
26.甲、乙两班共有84人,甲班人数的与乙班人数的共57人。求两班各有多少人?
27.下面是王明从家坐出租车去展览馆的路线图。已知出租车在3千米以内(含3千米)按起步价9元计算,外加1元燃油附加费,以后每增加1千米,车费就增加1.6元。请你按图中提供的信息算一算:王明从家经过文化馆最后到展览馆,一共要付多少元车费?
28.为迎接新年,惠民商场推出一系列的优惠活动。
①在网上用55元买100元的代金券(100元代金券到店可当现金使用,每次消费只能使用一张,且不可找零)。
②消费后按照实际价格打七折付款。
③消费每满100元减40元,不足100元的部分不减。
王阿姨在商场购买了总价450元的物品,她应该选择哪种优惠方式最合算?为什么?
29.小明爸爸打开了一个长方体的快递包装盒,如图是其表面展开图。经测量,厘米,厘米(、、表示线段的长度),求这个长方体的表面积和体积。
参考答案
1.D
应用生活常识,正确使用厘米、克、毫升、公顷这四个单位。1厘米就是大约一个手指甲盖的宽度;一枚回形针大约重 1 克;最常见的瓶装水的容积是500毫升的;公顷是边长为100米的正方形的面积,即1公顷=10000平方米,表示某个地区我们一般常用平方千米;据此逐项分析即可解答。
A.衡量一个人的身高我们经常使用厘米,六年级学生平均身高约145厘米,该选项说法符合常识;
B.一枚回形针大约重 1 克,一枚鸡蛋重约60克,该选项说法符合常识;
C.最常见的瓶装水的容积是500毫升的,一瓶普通的牛奶大约250毫升,该选项说法符合常识;
D.1公顷=10000平方米,公顷常用来表示操场的大小,表示某个地区的大小不适合,应选用平方千米,所以该选项说法不符合常识。
故答案为:D
2.A
根据最小公倍数的定义,如果一个数是另一个数的倍数,那么它们的最小公倍数就是较大的数。已知a÷b=c(a、b、c均为整数,且b≠0),这意味着a是b的倍数。
因为a÷b=c(a、b、c均为整数,且b≠0),所以a是b的倍数,同时a也是它自身的倍数,所以a和b的最小公倍数是a。
故答案为:A
3.C
采用赋值法进行分析,假设=1,将=1分别代入和,计算出结果,比较并求差即可。
假设=1。
=5×1+8
=5+8
=13
13<45
45-13=32
结果与原式比较少32。
故答案为:C
4.D
根据图,分别找出数量关系式,列出方程判断。
A.由图可知,3段为,1段为,60则是,因此该图可用表示;
B.由图可知,大三角形和小三角形是等高的三角形,小三角形的底是5,大三角形的底是15,5是15的,所以小三角形的面积是大三角形的面积的,即小三角形的面积是x(cm2),小三角形的面积+大三角形的面积=60,所以列式是x+x=60,所以选项B可以用x+x=60表示;
C.由图可知,圆柱和圆锥等底等高,则圆锥的体积是圆柱体积的,圆锥体积+圆柱体积=60,所以该图可用表示;
D.由图可知,2段为,1段为,60则是,因此该图不可用表示。
故答案为:D
5.B
可以把选项中的几种情况列出来是由几加几构成的,第一个加数是第一个骰子,第二个加数是第二个骰子,据此分析:数字和是6的情况有:1+5;2+4;3+3;4+2;5+1;有5种情况;数字和是7的情况有:1+6;2+5;3+4;4+3;5+2;6+1;有6种情况;数字和是8的情况有2+6;3+5;4+4;5+3;6+2;有5种情况;数字和是9的情况有3+6;4+5;5+4;6+3;有4种情况;所以出现数字和是7的可能性大,据此解答。
根据分析可知,一个骰子六个面上分别有数字1,2,3,4,5,6,任意抛两次,上面的数字和是7的可能性大。
故答案为:B
解答本题的关键是明确数字出现的次数多少。
6.C
考虑最倒霉的情况,取出的前5个都是黄乒乓球,再取两个,一定是2个白乒乓球,据此解答。
5+2=7(个)
一个盒子里有黄、白乒乓球各5个,要想使取出的乒乓球保证至少有2个白色的,则至少取出的个数是7。
故答案为:C
7.B
已知甲、乙两个圆的直径比是2∶3,根据圆的直径d=2r可知,甲、乙两个圆的半径比也是2∶3;可以设甲圆的半径为2,乙圆的半径为3; 根据圆的面积公式S=πr2,分别求出两个圆的面积,再根据比的意义写出两个圆的面积之比,然后化简比即可。
设甲圆半径为2,则乙圆半径为3,
甲圆面积:π×22=4π
乙圆面积:π×32=9π
甲圆面积∶乙圆面积=4π∶9π=4∶9
故答案为:B
8.24;21;10;60
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
分数化成小数,用分子除以分母即可;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号。
==,=24÷40
==,=21∶35
==
=3÷5=0.6
0.6=60%
即24÷40==21∶35==60%。
9.74
比0℃低的温度叫零下温度,通常在数字前面加“﹣”(负号);比0℃高的温度叫零上温度,通常在数字前面加“﹢”(正号),也可以省略不写。
根据题意,最高温度是42摄氏度,与0摄氏度相差42摄氏度;最低温度是﹣32摄氏度,与0摄氏度相差32摄氏度;所以最高温度与最低温度相差(42+32)摄氏度。
42+32=74(摄氏度)
最高温度与最低温度相差74摄氏度。
10. 1.303
把分数、百分数化成小数,循环小数写成小数形式,再根据小数比较大小的方法:先看整数部分,整数部分大的那个数就大;如果整数部分相同,就看十分位上的数,十分位上的数大的那个数就大;如果十分位上的数也相同,就看百分位上的数,百分位上的数大的那个数就大,……,依此类推,进行解答。
=1.333…
133.4%=1.334
=1.303030…
1.334>1.333…>1.303030…>1.303,即133.4%>>>1.303。
1.303,,,,四个数中,最大的是133.4%,最小的1.303。
11./0.125
已知A和B互为倒数,根据倒数的意义可得AB=1;
根据比例的基本性质把=改写成两数相乘的形式即8C=AB,然后把AB=1代入式子中,计算出C的值即可。
乘积是1的两个数互为倒数。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
A和B互为倒数,则AB=1;
由=可得:8C=AB;
把AB=1代入8C=AB,可得:
8C=1
C=1÷8
C=
A和B互为倒数,且=,那么C=()。
12. 75m2 120
求60m2比哪个数少20%,把要求的数看作单位 “1”; 则60m2是这个数的(1 20%),已知一个数的百分之几是多少,求这个数用除法,所以这个数为:60÷(1 20%);把80dm看作单位 “1”,要求的数比80dm多,那么要求的数是80dm的(1+ ),求一个数的几分之几是多少用乘法,则这个数为:80×(1+ )。
60÷(1-20%)
=60÷80%
=60÷0.8
=75(m2)
80×(1+ )
=80×
=120(dm)
60m2比75 m2少20%,比80dm多的是120dm。
13. /0.6
分析题目,把这根铁丝看作单位“1”,用铁丝的总长度除以分成的段数即可得到每段长多少米;再用分成的总段数除以小明拿的段数即可得到小明拿的铁丝是这根铁丝的几分之几。
3÷5=(m)
2÷5=
把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长,小明拿的铁丝是这根铁丝的(填上合适的分数)。
14.720
二成就是20%,把去年收大豆的重量看作单位“1”,今年比去年减产20%,求出今年大豆减产的重量,用去年收大豆的重量×20%解答。
3600×20%=720(kg)
去年收大豆3600kg,今年比去年减产二成,今年大豆减产720kg。
15.7
若每个花束的康乃馨和粉百合花的朵数相同,说明康乃馨和粉百合花都是等分的,而且分的份数相同,要使每束花里花朵数最少,只要求出96和72的最大公因数,即可获得花束数,花的总数96+72除以花束数,就得到每个花束里至少有多少朵花。
96=2×2×2×2×2×3
72=2×2×2×3×3
96和72的最大公因数:2×2×2×3=24
96÷24+72÷24
=4+3
=7(朵)
每束花里至少有7朵花。
16. 60 120
当奶糖全部用完,则说明奶糖用了180千克,由于什锦糖中奶糖是3份,用180÷3即可求出1份量,再乘酥糖和水果糖的份数即可求出需要酥糖和水果糖的质量,用180减去需要酥糖的质量即可求出还有多少千克酥糖,再用水果糖需要的质量减去180即可求出需要添加多少千克水果糖。
180-180÷3×2
=180-60×2
=180-120
=60(千克)
180÷3×5
=60×5
=300(千克)
300-180=120(千克)
酥糖还剩60千克,水果糖则需要增加120千克。
17. 37.68
分析题目,削成的最大的圆锥和圆柱是等底等高的,即圆锥的底面直径就等于圆柱的底面直径,圆锥的高就等于圆柱的高,据此结合圆锥的体积=π(d÷2)2h代入数据求出圆锥的体积即可;圆锥的体积是和它等底等高的圆柱体积的,把圆柱的体积看作单位“1”,则削去的木块的体积是圆柱体积的(1-),据此用除法求出削成最大圆锥的体积是削去木块体积几分之几即可。
3.14×(4÷2)2×9×
=3.14×22×9×
=3.14×4×9×
=12.56×9×
=113.04×
=37.68(cm3)
÷(1-)
=÷
=×
=
用一个底面直径是4cm,高为9cm的圆柱木块,削成一个最大的圆锥,圆锥的体积是37.68cm3,削成最大圆锥的体积是削去木块体积的。
18.1072;1.6;;25
20;;;0
19.300;10
;
先把除法变为乘法:×12.5××8,再根据乘法交换律和结合律把原式变为:(×)×(12.5×8)进行简算;
先算小括号里的加法,再算中括号里的乘法,最后算中括号外的除法;
先把除法变为乘法:×+×+×,再根据乘法分配律的逆运算:a×b+a×c=a×(b+c),把原式化为(++)×进行简算;
先算小括号里的加法,再算中括号里的除法,最后算中括号外的除法。
=×12.5××8
=(×)×(12.5×8)
=3×100
=300
10.4÷[(0.64+1.44)×0.5]
=10.4÷[2.08×0.5]
=10.4÷1.04
=10
=×+×+×
=(++)×
=1×
=
÷[(1+)÷]
=÷[÷]
=÷[×]
=÷2
=×
=
20.x=1.2;x=;x=20
(1)先计算等式左边的乘法,根据减数等于被减数减差,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时除以12,等式仍然成立,计算即可得解;
(2)先计算等式左边的加法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时除以,等式仍然成立,计算即可得解;
(3)先计算等式左边的乘法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时乘,等式两边再同时除以,等式仍然成立,计算即可得解。
9×1.8-12x=1.8
解:16.2-12x=1.8
16.2-12x+12x=1.8+12x
1.8+12x=16.2
1.8+12x-1.8=16.2-1.8
12x=14.4
12x÷12=14.4÷12
x=1.2
解:x=
x÷=÷
x=×
x=
解:=
5÷32x=
5÷32x×32x=×32x
x=5
x÷=5÷
x=5×4
x=20
21.14.25平方厘米
由图可知,这个平行四边形的高等于这个圆的半径、平行四边形的底等于这个圆的直径。我们可设圆的半径为r,则平行四边形的底=2r,高=r,因为平行四边形的面积是100平方厘米,根据平行四边形的面积=底×高,即2r×r=100,所以r2=100÷2=50。阴影部分的面积是圆的面积的减去等腰三角形ABO的面积,圆的面积=,三角形的面积=r×r×=r2,把r2=50代入式子中即可解答。
100÷2=50(平方厘米)
3.14×50×-50×
=39.25-25
=14.25(平方厘米)
阴影部分的面积是14.25平方厘米。
22.(1)1∶30000;
(2)图见详解
(1)根据图上距离∶实际距离=比例尺,用图上距离和实际距离的比化成前项是1的比,即是比例尺;
(2)先实际距离除以比例尺,求出图上距离,再根据给的角度和方向画图。
(1)600米=60000厘米
2厘米∶600米
=2∶60000
=1∶30000
则这幅图的比例尺是1∶30000;
(2)900米=90000厘米
90000×=3(厘米)
23.(1)(2)(3)见详解
(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到轴对称图形①的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形①的另一半;
(2)把图形②各边放大到原来的2倍后的图形,即图形②各边的长度都要乘2,放大后图形的形状不变,据此画出放大后的图形;
(3)根据旋转的特征,将图形③绕点C逆时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形;据此作图。
(1)(2)(3)如图:
24.小华2550元;小明255元
根据题意,小华的存款数个位数字是0,如果把0去掉,就和小明的存款同样多,说明小华的存款是小明存款的10倍;把小明的存款看作1份,小华的存款看作10份,一共是(1+10)份;
已知小华和小明共有存款2805元,用两人的总存款除以总份数,求出一份数,即是小明的存款;再用小明的存款乘10,求出小华的存款。
小明:
2805÷(1+10)
=2805÷11
=255(元)
小华:255×10=2550(元)
答:小华有存款2550元,小明有存款255元。
25.24页;100页
第一天与第二天看的页数比是5∶6,即第二天看的页数是第一天的,用第一天看的页数×,求出第二天看的页数;再把第一天看到页数与第二天看的页数相加,求出两天一共看的页数;把这本书的总页数看作单位“1”,两天一共看了这本书的,对应的是两天一共看的页数,求单位“1”,用两天一共看的页数÷,即可求出这本数的总页数,据此解答。
20×=24(页)
(20+24)÷
=44÷
=44×
=100(页)
答:她第二天看了24页,这本书有100页。
26.甲班48人;乙班36人
根据“甲、乙两班共有84人”,可以设乙班有人,则甲班有(84-)人;
根据“甲班人数的与乙班人数的共57人”可得出等量关系:甲班人数×+乙班人数×=57,据此列出方程,并求解。
解:设乙班有人,则甲班有(84-)人。
(84-)×+=57
84×-+=57
52.5-+=57
52.5+=57
=57-52.5
=4.5
=4.5÷
=4.5×8
=36
甲班:84-36=48(人)
答:甲班有48人,乙班有36人。
27.53.2元
从图中可知,这幅路线图的比例尺是1∶250000,从王明家到展览馆的图上距离是(8+4)厘米,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出从王明家到展览馆的实际距离为30千米。
因为实际距离30千米超过3千米,所以分两段收费:
第一段,行程3千米,收费9元;
第二段,超过3千米的部分,单价1.6元,行程为(30-3)千米,根据“单价×数量=总价”,求出这一段的费用;
然后把这两段的费用相加,再加上1元的燃油附加费,即是一共要付的车费。
8+4=12(厘米)
12÷
=12×250000
=3000000(厘米)
3000000厘米=30千米
9+1.6×(30-3)+1
=9+1.6×27+1
=9+43.2+1
=53.2(元)
答:一共要付53.2元车费。
28.选择第③种优惠方式最合算。因为第③种优惠活动最便宜。
①王阿姨购买的总价是450元,用一张代金券,即花55元抵100元,可列式。
②打七折,即把原价看作单位“1”,实际购买价格是原价的70%,根据求一个数的百分之几是多少,用乘法计算,可列式。
③先用除法计算450中有几个100,就用450减几个40。
分别求出三种优惠方式的实际钱数,比较即可。
①
(元)
②七折=70%
(元)
③(次)50(元)
(元)
答:她应该选择第③种优惠方式最合算。因为第③种优惠活动最便宜。
29.112平方厘米;64立方厘米
设长方体的长、宽、高分别为,,,根据图形条件可得,(厘米),即(厘米);(厘米);厘米;故可得,(厘米),(厘米),(厘米),再根据和计算公式即可解答。
解:设长方体的长、宽、高分别为,,。
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
长方体表面积:
(平方厘米)
长方体体积为:
(立方厘米)
答:这个长方体的表面积是112平方厘米,体积是64立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024--2025学年小学毕业会考数学人教版模拟试卷一
一、选择题
1.下面的描述中不符合日常生活常识的是( )。
A.六年级学生平均身高约145厘米 B.一枚鸡蛋重约60克
C.一瓶普通的牛奶大约250毫升 D.黄山市的总面积9807公顷
2.如果a÷b=c(a、b、c均为整数,且b≠0),那么a和b的最小公倍数是( )。
A.a B.b C.c D.无法确定
3.小明误将错写成,结果与原式比较( )。
A.少5 B.少8 C.少32 D.和原来一样
4.下面不能用方程“”表示的是( )。
A. B.
C. D.
5.一个骰子六个面上分别有数字1,2,3,4,5,6,任意抛两次,上面的数字和是( )的可能性大。
A.6 B.7 C.8 D.9
6.一个盒子里有黄、白乒乓球各5个,要想使取出的乒乓球保证至少有2个白色的,则至少取出的个数是( )。
A.3 B.6 C.7 D.10
7.甲、乙两个圆的直径比是2∶3,那么甲、乙两个圆的面积比是( )。
A.1∶8 B.4∶9 C.2∶3 D.3.14∶7.065
二、填空题
8.( )÷40==( )∶35==( )%。
9.我国某地一年中最高温度是42摄氏度,最低温度是﹣32摄氏度,最高温度与最低温度相差( )摄氏度。
10.比一比:1.303,,,,四个数中,最大的是( ),最小的是( )。
11.A和B互为倒数,且=,那么C=( )。
12.60m2比( )少20%,比80dm多的是( )dm。
13.把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长( ),小明拿的铁丝是这根铁丝的( )(填上合适的分数)。
14.去年收大豆3600kg,今年比去年减产二成,今年大豆减产( )kg。
15.用96朵康乃馨和72朵粉百合做成花束,每束花里的康乃馨朵数相同,粉百合朵数也相同,每束花里至少有( )朵花。
16.一种什锦糖是由酥糖、奶糖和水果糖按2∶3∶5混合配制而成的。如果这三种糖都有180千克,当奶糖全部用完时,酥糖还剩( )千克;水果糖则需要增加( )千克。
17.用一个底面直径是4cm,高为9cm的圆柱木块,削成一个最大的圆锥,圆锥的体积是( )cm3,削成最大圆锥的体积是削去木块体积的( )。
三、计算题
18.直接写出得数。
873+199= 0.64÷0.4= = 20×5÷20×5=
= = = =
19.脱式计算,能简算的要简算。
10.4÷[(0.64+1.44)×0.5]
20.解方程。
9×1.8-12x=1.8
21.如图,已知平行四边形的面积是100平方厘米。求阴影部分的面积。
四、作图题
22.(1)学校在中心广场北偏西60°方向600米处,这幅图的比例尺是( )。
(2)书店在中心广场南偏东50°方向900米处,请在图中用“ ”标出书店的位置。
23.在方格纸中,按要求画一画。
(1)以虚线为对称轴,画出轴对称图形①的另一半。
(2)画出把图形②各边放大到原来的2倍后的图形。
(3)画出图形③绕点C逆时针旋转90°后的图形。
五、解答题
24.小华和小明共有存款2805元,其中小华的存款数个位数字是0,如果把0去掉,就和小明的存款同样多。小华、小明各有存款多少元?
25.小红看一本书,两天一共看了这本书的。已知第一天看了20页,第一天与第二天看的页数比是5∶6,她第二天看了多少页?这本书有多少页?
26.甲、乙两班共有84人,甲班人数的与乙班人数的共57人。求两班各有多少人?
27.下面是王明从家坐出租车去展览馆的路线图。已知出租车在3千米以内(含3千米)按起步价9元计算,外加1元燃油附加费,以后每增加1千米,车费就增加1.6元。请你按图中提供的信息算一算:王明从家经过文化馆最后到展览馆,一共要付多少元车费?
28.为迎接新年,惠民商场推出一系列的优惠活动。
①在网上用55元买100元的代金券(100元代金券到店可当现金使用,每次消费只能使用一张,且不可找零)。
②消费后按照实际价格打七折付款。
③消费每满100元减40元,不足100元的部分不减。
王阿姨在商场购买了总价450元的物品,她应该选择哪种优惠方式最合算?为什么?
29.小明爸爸打开了一个长方体的快递包装盒,如图是其表面展开图。经测量,厘米,厘米(、、表示线段的长度),求这个长方体的表面积和体积。
参考答案
1.D
应用生活常识,正确使用厘米、克、毫升、公顷这四个单位。1厘米就是大约一个手指甲盖的宽度;一枚回形针大约重 1 克;最常见的瓶装水的容积是500毫升的;公顷是边长为100米的正方形的面积,即1公顷=10000平方米,表示某个地区我们一般常用平方千米;据此逐项分析即可解答。
A.衡量一个人的身高我们经常使用厘米,六年级学生平均身高约145厘米,该选项说法符合常识;
B.一枚回形针大约重 1 克,一枚鸡蛋重约60克,该选项说法符合常识;
C.最常见的瓶装水的容积是500毫升的,一瓶普通的牛奶大约250毫升,该选项说法符合常识;
D.1公顷=10000平方米,公顷常用来表示操场的大小,表示某个地区的大小不适合,应选用平方千米,所以该选项说法不符合常识。
故答案为:D
2.A
根据最小公倍数的定义,如果一个数是另一个数的倍数,那么它们的最小公倍数就是较大的数。已知a÷b=c(a、b、c均为整数,且b≠0),这意味着a是b的倍数。
因为a÷b=c(a、b、c均为整数,且b≠0),所以a是b的倍数,同时a也是它自身的倍数,所以a和b的最小公倍数是a。
故答案为:A
3.C
采用赋值法进行分析,假设=1,将=1分别代入和,计算出结果,比较并求差即可。
假设=1。
=5×1+8
=5+8
=13
13<45
45-13=32
结果与原式比较少32。
故答案为:C
4.D
根据图,分别找出数量关系式,列出方程判断。
A.由图可知,3段为,1段为,60则是,因此该图可用表示;
B.由图可知,大三角形和小三角形是等高的三角形,小三角形的底是5,大三角形的底是15,5是15的,所以小三角形的面积是大三角形的面积的,即小三角形的面积是x(cm2),小三角形的面积+大三角形的面积=60,所以列式是x+x=60,所以选项B可以用x+x=60表示;
C.由图可知,圆柱和圆锥等底等高,则圆锥的体积是圆柱体积的,圆锥体积+圆柱体积=60,所以该图可用表示;
D.由图可知,2段为,1段为,60则是,因此该图不可用表示。
故答案为:D
5.B
可以把选项中的几种情况列出来是由几加几构成的,第一个加数是第一个骰子,第二个加数是第二个骰子,据此分析:数字和是6的情况有:1+5;2+4;3+3;4+2;5+1;有5种情况;数字和是7的情况有:1+6;2+5;3+4;4+3;5+2;6+1;有6种情况;数字和是8的情况有2+6;3+5;4+4;5+3;6+2;有5种情况;数字和是9的情况有3+6;4+5;5+4;6+3;有4种情况;所以出现数字和是7的可能性大,据此解答。
根据分析可知,一个骰子六个面上分别有数字1,2,3,4,5,6,任意抛两次,上面的数字和是7的可能性大。
故答案为:B
解答本题的关键是明确数字出现的次数多少。
6.C
考虑最倒霉的情况,取出的前5个都是黄乒乓球,再取两个,一定是2个白乒乓球,据此解答。
5+2=7(个)
一个盒子里有黄、白乒乓球各5个,要想使取出的乒乓球保证至少有2个白色的,则至少取出的个数是7。
故答案为:C
7.B
已知甲、乙两个圆的直径比是2∶3,根据圆的直径d=2r可知,甲、乙两个圆的半径比也是2∶3;可以设甲圆的半径为2,乙圆的半径为3; 根据圆的面积公式S=πr2,分别求出两个圆的面积,再根据比的意义写出两个圆的面积之比,然后化简比即可。
设甲圆半径为2,则乙圆半径为3,
甲圆面积:π×22=4π
乙圆面积:π×32=9π
甲圆面积∶乙圆面积=4π∶9π=4∶9
故答案为:B
8.24;21;10;60
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
分数与除法的关系:分子相当于被除数,分母相当于除数,分数线相当于除号;
分数与比的关系:分子相当于比的前项,分母相当于比的后项,分数线相当于比号;
分数化成小数,用分子除以分母即可;
小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号。
==,=24÷40
==,=21∶35
==
=3÷5=0.6
0.6=60%
即24÷40==21∶35==60%。
9.74
比0℃低的温度叫零下温度,通常在数字前面加“﹣”(负号);比0℃高的温度叫零上温度,通常在数字前面加“﹢”(正号),也可以省略不写。
根据题意,最高温度是42摄氏度,与0摄氏度相差42摄氏度;最低温度是﹣32摄氏度,与0摄氏度相差32摄氏度;所以最高温度与最低温度相差(42+32)摄氏度。
42+32=74(摄氏度)
最高温度与最低温度相差74摄氏度。
10. 1.303
把分数、百分数化成小数,循环小数写成小数形式,再根据小数比较大小的方法:先看整数部分,整数部分大的那个数就大;如果整数部分相同,就看十分位上的数,十分位上的数大的那个数就大;如果十分位上的数也相同,就看百分位上的数,百分位上的数大的那个数就大,……,依此类推,进行解答。
=1.333…
133.4%=1.334
=1.303030…
1.334>1.333…>1.303030…>1.303,即133.4%>>>1.303。
1.303,,,,四个数中,最大的是133.4%,最小的1.303。
11./0.125
已知A和B互为倒数,根据倒数的意义可得AB=1;
根据比例的基本性质把=改写成两数相乘的形式即8C=AB,然后把AB=1代入式子中,计算出C的值即可。
乘积是1的两个数互为倒数。
比例的基本性质:在比例里,两个外项的积等于两个内项的积。
A和B互为倒数,则AB=1;
由=可得:8C=AB;
把AB=1代入8C=AB,可得:
8C=1
C=1÷8
C=
A和B互为倒数,且=,那么C=()。
12. 75m2 120
求60m2比哪个数少20%,把要求的数看作单位 “1”; 则60m2是这个数的(1 20%),已知一个数的百分之几是多少,求这个数用除法,所以这个数为:60÷(1 20%);把80dm看作单位 “1”,要求的数比80dm多,那么要求的数是80dm的(1+ ),求一个数的几分之几是多少用乘法,则这个数为:80×(1+ )。
60÷(1-20%)
=60÷80%
=60÷0.8
=75(m2)
80×(1+ )
=80×
=120(dm)
60m2比75 m2少20%,比80dm多的是120dm。
13. /0.6
分析题目,把这根铁丝看作单位“1”,用铁丝的总长度除以分成的段数即可得到每段长多少米;再用分成的总段数除以小明拿的段数即可得到小明拿的铁丝是这根铁丝的几分之几。
3÷5=(m)
2÷5=
把一根长3m的铁丝平均分成5段,小明拿了其中的2段,每段长,小明拿的铁丝是这根铁丝的(填上合适的分数)。
14.720
二成就是20%,把去年收大豆的重量看作单位“1”,今年比去年减产20%,求出今年大豆减产的重量,用去年收大豆的重量×20%解答。
3600×20%=720(kg)
去年收大豆3600kg,今年比去年减产二成,今年大豆减产720kg。
15.7
若每个花束的康乃馨和粉百合花的朵数相同,说明康乃馨和粉百合花都是等分的,而且分的份数相同,要使每束花里花朵数最少,只要求出96和72的最大公因数,即可获得花束数,花的总数96+72除以花束数,就得到每个花束里至少有多少朵花。
96=2×2×2×2×2×3
72=2×2×2×3×3
96和72的最大公因数:2×2×2×3=24
96÷24+72÷24
=4+3
=7(朵)
每束花里至少有7朵花。
16. 60 120
当奶糖全部用完,则说明奶糖用了180千克,由于什锦糖中奶糖是3份,用180÷3即可求出1份量,再乘酥糖和水果糖的份数即可求出需要酥糖和水果糖的质量,用180减去需要酥糖的质量即可求出还有多少千克酥糖,再用水果糖需要的质量减去180即可求出需要添加多少千克水果糖。
180-180÷3×2
=180-60×2
=180-120
=60(千克)
180÷3×5
=60×5
=300(千克)
300-180=120(千克)
酥糖还剩60千克,水果糖则需要增加120千克。
17. 37.68
分析题目,削成的最大的圆锥和圆柱是等底等高的,即圆锥的底面直径就等于圆柱的底面直径,圆锥的高就等于圆柱的高,据此结合圆锥的体积=π(d÷2)2h代入数据求出圆锥的体积即可;圆锥的体积是和它等底等高的圆柱体积的,把圆柱的体积看作单位“1”,则削去的木块的体积是圆柱体积的(1-),据此用除法求出削成最大圆锥的体积是削去木块体积几分之几即可。
3.14×(4÷2)2×9×
=3.14×22×9×
=3.14×4×9×
=12.56×9×
=113.04×
=37.68(cm3)
÷(1-)
=÷
=×
=
用一个底面直径是4cm,高为9cm的圆柱木块,削成一个最大的圆锥,圆锥的体积是37.68cm3,削成最大圆锥的体积是削去木块体积的。
18.1072;1.6;;25
20;;;0
19.300;10
;
先把除法变为乘法:×12.5××8,再根据乘法交换律和结合律把原式变为:(×)×(12.5×8)进行简算;
先算小括号里的加法,再算中括号里的乘法,最后算中括号外的除法;
先把除法变为乘法:×+×+×,再根据乘法分配律的逆运算:a×b+a×c=a×(b+c),把原式化为(++)×进行简算;
先算小括号里的加法,再算中括号里的除法,最后算中括号外的除法。
=×12.5××8
=(×)×(12.5×8)
=3×100
=300
10.4÷[(0.64+1.44)×0.5]
=10.4÷[2.08×0.5]
=10.4÷1.04
=10
=×+×+×
=(++)×
=1×
=
÷[(1+)÷]
=÷[÷]
=÷[×]
=÷2
=×
=
20.x=1.2;x=;x=20
(1)先计算等式左边的乘法,根据减数等于被减数减差,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时除以12,等式仍然成立,计算即可得解;
(2)先计算等式左边的加法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时除以,等式仍然成立,计算即可得解;
(3)先计算等式左边的乘法,再根据等式的性质2:等式的左右两边同时乘(或除以)同一个不为0的数,等式两边同时乘,等式两边再同时除以,等式仍然成立,计算即可得解。
9×1.8-12x=1.8
解:16.2-12x=1.8
16.2-12x+12x=1.8+12x
1.8+12x=16.2
1.8+12x-1.8=16.2-1.8
12x=14.4
12x÷12=14.4÷12
x=1.2
解:x=
x÷=÷
x=×
x=
解:=
5÷32x=
5÷32x×32x=×32x
x=5
x÷=5÷
x=5×4
x=20
21.14.25平方厘米
由图可知,这个平行四边形的高等于这个圆的半径、平行四边形的底等于这个圆的直径。我们可设圆的半径为r,则平行四边形的底=2r,高=r,因为平行四边形的面积是100平方厘米,根据平行四边形的面积=底×高,即2r×r=100,所以r2=100÷2=50。阴影部分的面积是圆的面积的减去等腰三角形ABO的面积,圆的面积=,三角形的面积=r×r×=r2,把r2=50代入式子中即可解答。
100÷2=50(平方厘米)
3.14×50×-50×
=39.25-25
=14.25(平方厘米)
阴影部分的面积是14.25平方厘米。
22.(1)1∶30000;
(2)图见详解
(1)根据图上距离∶实际距离=比例尺,用图上距离和实际距离的比化成前项是1的比,即是比例尺;
(2)先实际距离除以比例尺,求出图上距离,再根据给的角度和方向画图。
(1)600米=60000厘米
2厘米∶600米
=2∶60000
=1∶30000
则这幅图的比例尺是1∶30000;
(2)900米=90000厘米
90000×=3(厘米)
23.(1)(2)(3)见详解
(1)根据轴对称图形的特征,对称点到对称轴的距离相等,找到轴对称图形①的各顶点关于对称轴的对称点后,依次连接各点得到轴对称图形①的另一半;
(2)把图形②各边放大到原来的2倍后的图形,即图形②各边的长度都要乘2,放大后图形的形状不变,据此画出放大后的图形;
(3)根据旋转的特征,将图形③绕点C逆时针旋转90°,点C位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形;据此作图。
(1)(2)(3)如图:
24.小华2550元;小明255元
根据题意,小华的存款数个位数字是0,如果把0去掉,就和小明的存款同样多,说明小华的存款是小明存款的10倍;把小明的存款看作1份,小华的存款看作10份,一共是(1+10)份;
已知小华和小明共有存款2805元,用两人的总存款除以总份数,求出一份数,即是小明的存款;再用小明的存款乘10,求出小华的存款。
小明:
2805÷(1+10)
=2805÷11
=255(元)
小华:255×10=2550(元)
答:小华有存款2550元,小明有存款255元。
25.24页;100页
第一天与第二天看的页数比是5∶6,即第二天看的页数是第一天的,用第一天看的页数×,求出第二天看的页数;再把第一天看到页数与第二天看的页数相加,求出两天一共看的页数;把这本书的总页数看作单位“1”,两天一共看了这本书的,对应的是两天一共看的页数,求单位“1”,用两天一共看的页数÷,即可求出这本数的总页数,据此解答。
20×=24(页)
(20+24)÷
=44÷
=44×
=100(页)
答:她第二天看了24页,这本书有100页。
26.甲班48人;乙班36人
根据“甲、乙两班共有84人”,可以设乙班有人,则甲班有(84-)人;
根据“甲班人数的与乙班人数的共57人”可得出等量关系:甲班人数×+乙班人数×=57,据此列出方程,并求解。
解:设乙班有人,则甲班有(84-)人。
(84-)×+=57
84×-+=57
52.5-+=57
52.5+=57
=57-52.5
=4.5
=4.5÷
=4.5×8
=36
甲班:84-36=48(人)
答:甲班有48人,乙班有36人。
27.53.2元
从图中可知,这幅路线图的比例尺是1∶250000,从王明家到展览馆的图上距离是(8+4)厘米,根据“实际距离=图上距离÷比例尺”以及进率“1千米=100000厘米”,求出从王明家到展览馆的实际距离为30千米。
因为实际距离30千米超过3千米,所以分两段收费:
第一段,行程3千米,收费9元;
第二段,超过3千米的部分,单价1.6元,行程为(30-3)千米,根据“单价×数量=总价”,求出这一段的费用;
然后把这两段的费用相加,再加上1元的燃油附加费,即是一共要付的车费。
8+4=12(厘米)
12÷
=12×250000
=3000000(厘米)
3000000厘米=30千米
9+1.6×(30-3)+1
=9+1.6×27+1
=9+43.2+1
=53.2(元)
答:一共要付53.2元车费。
28.选择第③种优惠方式最合算。因为第③种优惠活动最便宜。
①王阿姨购买的总价是450元,用一张代金券,即花55元抵100元,可列式。
②打七折,即把原价看作单位“1”,实际购买价格是原价的70%,根据求一个数的百分之几是多少,用乘法计算,可列式。
③先用除法计算450中有几个100,就用450减几个40。
分别求出三种优惠方式的实际钱数,比较即可。
①
(元)
②七折=70%
(元)
③(次)50(元)
(元)
答:她应该选择第③种优惠方式最合算。因为第③种优惠活动最便宜。
29.112平方厘米;64立方厘米
设长方体的长、宽、高分别为,,,根据图形条件可得,(厘米),即(厘米);(厘米);厘米;故可得,(厘米),(厘米),(厘米),再根据和计算公式即可解答。
解:设长方体的长、宽、高分别为,,。
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
(厘米)
长方体表面积:
(平方厘米)
长方体体积为:
(立方厘米)
答:这个长方体的表面积是112平方厘米,体积是64立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
