期中综合试卷 2024--2025学年小学数学人教版六年级下册
文档属性
| 名称 | 期中综合试卷 2024--2025学年小学数学人教版六年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 859.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 17:45:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期中综合试卷
2024--2025学年小学数学人教版六年级下册
一、选择题
1.下面各选项中的两种量成反比例的是( )。
A.圆的半径和面积。 B.李师傅8小时做的零件个数和工作效率。
C.从介休到太原,汽车行驶的时间和速度。 D.小栋的身高和他的体重。
2.解决图中的问题,列式正确的是( )。
A.180×(1-20%) B.180÷(1-20%) C.180×(1+20%) D.180÷(1+20%)
3.下面使用转化思想解决问题的是( )。
A.①② B.①②③ C.②③④ D.①②③④
4.圆锥的侧面展开图的形状是( )。
A.扇形 B.圆形 C.三角形 D.等腰三角形
5.按下面的程序操作,输入的数a与计算结果b之间的关系是怎样的?( )
输入a(不为0的自然数) → → → 输出计算结果b
A.a与b成正比例关系 B.a与b成反比例关系
C.a与b不成比例 D.无法判断a与b是否成比例
6.小明发现他的铅笔头是圆锥形,笔杆是圆柱形,且圆柱的长是圆锥的3倍,那么圆柱的体积是圆锥的( )倍。
A.3 B.6 C.9 D.27
二、填空题
7.在﹣6、3、0、﹣18、﹢7中,( )是正数,( )是负数,( )既不是正数,也不是负数。
8.一个圆柱的体积是80cm3,底面积是16cm2。它的高是( )厘米。
9.小兰去学校时向东走500米,返回时应向( )行走( )米。
10.一本课外书,原价40元,现在按八五折优惠销售,比原价便宜了( )元。
11.在一个比例里,两外项互为倒数,一个内项是0.8,另一个内项是( )。
12.在一幅地图上量得两地间的距离是3cm,已知两地的实际距离是15km,这幅地图的比例尺是( );在比例尺为1∶2000的地图上,6cm的线段代表实际距离( )m,实际距离180m在图上要画( )cm。
13.一个圆柱的底面半径是3cm,高是10cm,它的侧面积是( )体积是( )。
14.一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是( )cm,和它等底等高的圆柱的体积是( )cm3。
三、计算题
15.直接写出下列各题的得数。
×= 47×20%= 2÷-÷2=
300÷5%= 0.42-0.43= 3r×6r=
16.怎样算简便就怎样算。
9.6-117%-5.83+11.4 (1.68+1.68+1.68+1.68)×2.5
3.1÷+3.1×20% 9×(-)×15 2025÷12.5%÷8
17.解比例。
3.36∶2.8=2.4∶ = 12∶(-2)=1∶
四、作图题
18.下面每个小正方形的边长表示1厘米。
(1)画出图形A按3∶1放大后得到的图形B。
(2)如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个( ),这个图形的体积是( )立方厘米。
五、解答题
19.介休103路内环公交车从起点站(火车站)开出,下面是它经过几个停靠站时上下车人数的记录表。(上车人数记为正)
车站名 火车站北 定阳饭店 政务中心 介休三中 介纺社区 北坛公园东
上车人数 ﹢9 ﹢7 ﹢6 0 ﹢5 ﹢1
下车人数 ﹣ ﹣3 0 ﹣4 ﹣3 ﹣5
(1)从火车站到北坛公园东站,途中无人上车的站是__________,无人下车的站是__________。
(2)这辆公交车从介休三中站开出时,车上有( )名乘客,从北坛公园东站开出时,车上有( )名乘客。
(3)介休103路所有乘客统一票价为1元,那么这趟公交车从北坛公园东站开出时,已经收入多少钱?
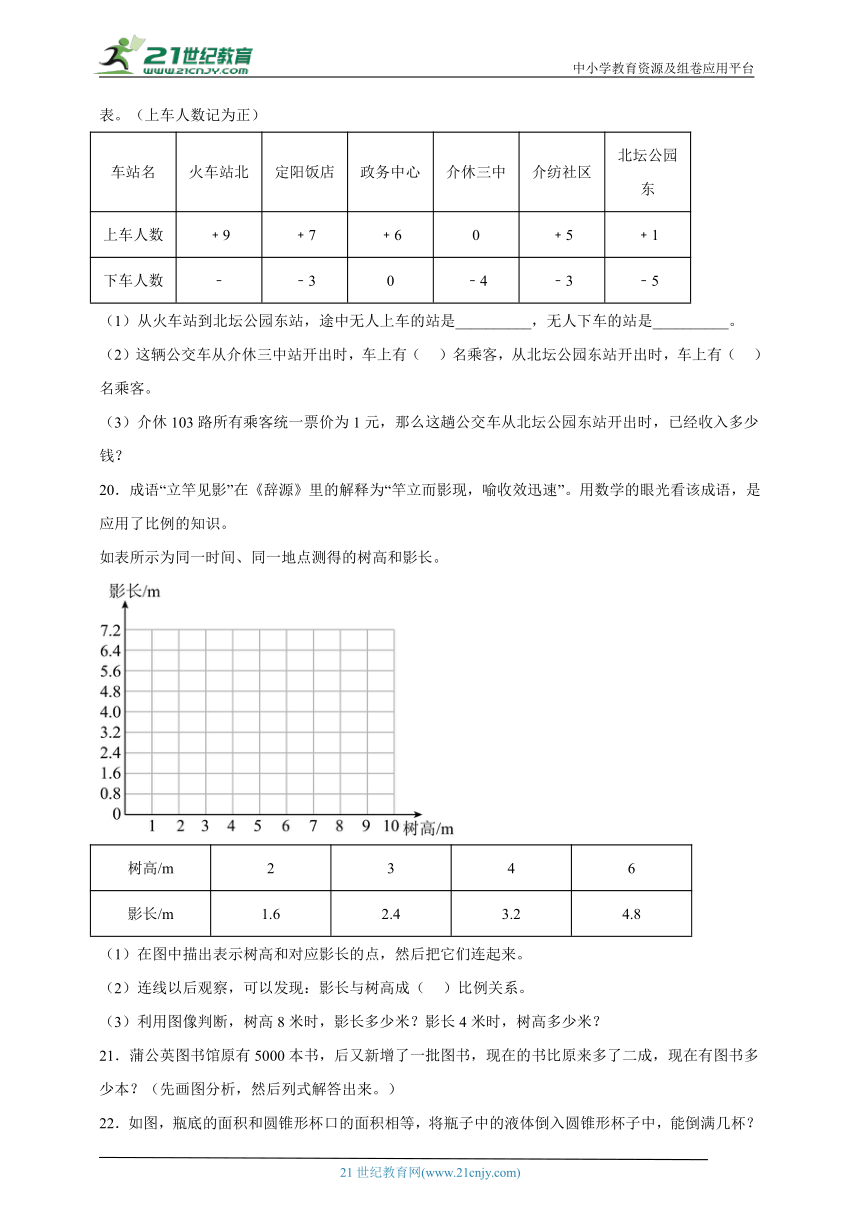
20.成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速”。用数学的眼光看该成语,是应用了比例的知识。
如表所示为同一时间、同一地点测得的树高和影长。
树高/m 2 3 4 6
影长/m 1.6 2.4 3.2 4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来。
(2)连线以后观察,可以发现:影长与树高成( )比例关系。
(3)利用图像判断,树高8米时,影长多少米?影长4米时,树高多少米?
21.蒲公英图书馆原有5000本书,后又新增了一批图书,现在的书比原来多了二成,现在有图书多少本?(先画图分析,然后列式解答出来。)
22.如图,瓶底的面积和圆锥形杯口的面积相等,将瓶子中的液体倒入圆锥形杯子中,能倒满几杯?(忽略瓶壁和杯壁的厚度)请把你的想法简洁地表达在下面。
23.显微镜是主要用于放大微小物体为人的肉眼所能看到的仪器。一个长为0.12毫米,宽为0.1毫米的近似长方形的细胞。在显微镜下的宽是2厘米,那么这个细胞在显微镜下的长是多少厘米?
24.一个圆锥形沙堆,底面积28.26平方米,高是2.7米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
25.“五一”快到了,聪聪一家计划开车从大同到介休旅游。
(1)根据地图请你计算大同到介休的实际距离是多少千米?(图上距离取整厘米)
(2)在另一幅地图上量得大同与介休的图上距离是14厘米,这幅地图的比例尺是多少?
参考答案
1.C
相关的两个量,如果它们的商一定,那么它们成正比例;如果它们的乘积一定,那么它们成反比例,据此逐项分析解答。
A.因为圆的面积÷半径=π×半径,π×半径随着半径的变化而变化,所以圆的面积和半径不成反比例关系;
B.李师傅工作8小时,零件总数÷工作效率=8小时(定值),零件总数与工作效率的商一定,而反比例关系要求两个量的乘积一定。所以李师傅8小时做的零件个数和工作效率不成反比例;
C.因为速度×时间=路程,从介休到太原两地路程一定,所以汽车行驶的速度和时间成反比例;
D.因为身高和体重会受到很多因素的影响,两者并没有严格的数学比例关系,所以小栋的身高和他的体重不成比例。
故答案为:C
2.D
以2023的产值为单位“1”,二成=20%,已知2024年的产值(180万元)相当于2023年的1+20%=120%,根据已知比一个数多百分之几是多少,求这个数用除法计算。用2024年的产值÷120%即可。
180÷(1+20%)
=180÷120%
=150(万元)
2023的产值为150万元。
故答案为:D
3.D
① 把圆柱的体积转化为长方体,利用长方体体积公式,推导出圆柱的体积公式,用了转化思想解决问题。
②把圆柱的侧面积转化为长方形,利用长方形面积公式,推导出圆柱的侧面积公式,用了转化思想解决问题。
③把瓶子中的液体转化为两个圆柱的容积,求出瓶子的容积,用了转化思想解决问题。
④把不规则物体的体积转化为圆柱的体积,求出不规则物体的体积,用了转化思想解决问题。据此解答。
根据分析可知,使用转化思想解决问题的是①②③④。
故答案为:D
4.A
圆锥的底面圆和侧面组成,侧面是连接底面圆周与顶点的曲面;将圆锥的侧面沿一条母线(从顶点到底面圆周的线段),剪开并摊平,曲面变为平面。展开后母线成为扇形的半径,底面圆的周长对应扇形的弧长,据此解答。
根据分析可知,圆锥的侧面展开图的形状是扇形。
故答案为:A
5.A
程序操作可得:a××=b。判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
a××=b可得:b÷a=×=
因为比值一定,所以a和b成正比例关系。
故答案为:A
6.C
圆锥和圆柱的底面半径相同,可以设为r,圆锥的高为,圆柱的高是圆锥的3倍,则圆柱的高为3h。分别根据圆柱的体积和圆锥的体积得出体积得出两个图形之间的关系。
设半径为r,圆锥的高为,圆柱的高为3h。
圆柱:
圆锥:
则圆柱的体积是圆锥的9倍。
故答案为:C
7. 3,﹢7 ﹣6,﹣18 0
根据正、负数的意义,大于0的数是正数,正数的前面有“﹢”号,也可以省略前面的“﹢”号;小于0的数是负数,负数的前面有“﹣”号,0既不是正数也不是负数,据此判断即可。
正数:3,﹢7;
负数:﹣6,﹣18。
在﹣6、3、0、﹣18、﹢7中,3,﹢7是正数,﹣6,﹣18是负数,0既不是正数,也不是负数。
8.5
圆柱体积=底面积×高,据此求解。
80÷16=5(cm),所以这个圆柱的高是5cm。
掌握圆柱的体积公式是解决本题的关键。
9. 西 500
规定某个方向为正,则相反方向即为负。
小兰去学校时向东走了500米,返回时应向相反的方向西走相同的距离500米。
10.6
打八五折,就是按原价的85%销售,便宜了1-85%,用原价×便宜的对应百分率即可。
40×(1-85%)
=40×0.15
=6(元)
比原价便宜了6元。
本题考查了百分数实际应用题,打折销售是商家常用的促销手段。
11.1.25//
互为倒数的两个数乘积为1,据此可知比例的外项之积是1,再根据比例的基本性质:两内项之积等于两外项之积可知两内项之积也等于1,据此用1除以一个内项即可得到另一个内项。
1÷0.8=1.25
在一个比例里,两外项互为倒数,一个内项是0.8,另一个内项是1.25。
12. 1∶500000/ 120 9
(1)先根据1km=100000cm把15km化成以cm为单位,再根据比例尺=图上距离∶实际距离求出比例尺即可;
(2)先根据实际距离=图上距离÷比例尺求出实际距离,再根据1m=100cm把结果换算成以m为单位即可;
(3)先根据1m=100cm把180m换算成以cm为单位,再根据图上距离=实际距离×比例尺求出图上距离即可。
15km=1500000cm
3cm∶1500000cm
=3∶1500000
=(3÷3)∶(1500000÷3)
=1∶500000
6÷=6×2000=12000(cm)
12000cm=120m
180m=18000cm
18000×=9(cm)
在一幅地图上量得两地间的距离是3cm,已知两地的实际距离是15km,这幅地图的比例尺是1∶500000;在比例尺为1∶2000的地图上,6cm的线段代表实际距离120m,实际距离180m在图上要画9cm。
13. 188.4 282.6
圆柱的侧面积S=Ch=2πrh;圆柱的体积V=Sh=πr2h;据此代入数据计算即可。
侧面积:3.14×3×2×10=188.4(cm2)
体积:3.14×32×10=282.6(cm3)
故答案为:188.4;282.6
本题主要考查圆柱的侧面积及体积的公式,牢记公式是解题的关键,解题时要细心。
14. 8 226.08
圆锥的高=圆锥的体积÷÷底面积,即可解答;圆锥体积是和它等底等高的圆柱的体积的,据此解答。
圆锥的高:
75.36÷÷[3.14×(6÷2)2]
=75.36×3÷28.26
=226.08÷28.26
=8(cm)
和它等底等高的圆柱的体积是:
75.36÷
=75.36×3
=226.08(cm3)
本题考查了圆锥高的求法以及已知圆锥体积求和它等底等高的圆柱的体积的方法,注意认真计算牢记公式。
15.;9.4;
6000;0.096;18r2
略
16.14;16.8
3.1;42;2025
(1)根据加法的交换律和结合律、减法的性质,将原式变成(9.6+11.4)-(117%+5.83),即可简算。
(2)根据乘法的意义,将原式变成1.68×4×2.5,再根据乘法的结合律,将算式变成1.68×(4×2.5),即可简算。
(3)先将原式变成3.1×+3.1×,再根据乘法分配律,将算式变成3.1×(+),即可简算。
(4)根据乘法交换律将原式变成9×15×(-),再根据乘法分配律,将算式变成9×15×-9×15×,即可简算。
(5)根据除法的性质,将原式变成2025÷(12.5%×8),即可简算。
9.6-117%-5.83+11.4
=(9.6+11.4)-(117%+5.83)
=21-7
=14
(1.68+1.68+1.68+1.68)×2.5
=1.68×4×2.5
=1.68×(4×2.5)
=1.68×10
=16.8
3.1÷+3.1×20%
=3.1×+3.1×
=3.1×(+)
=3.1×1
=3.1
9×(-)×15
=9×15×(-)
=9×15×-9×15×
=60-18
=42
2025÷12.5%÷8
=2025÷(12.5%×8)
=2025÷1
=2025
17.=2;=37.5;=10
(1)先根据比例的基本性质将比例方程改写成3.36=2.8×2.4,然后方程两边同时除以3.36,求出方程的解;
(2)先根据比例的基本性质将比例方程改写成8=20×15,然后方程两边同时除以8,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成(-2)×1=12×,然后把方程化简成-2=8,方程两边再同时加上2,求出方程的解。
(1)3.36∶2.8=2.4∶
解:3.36=2.8×2.4
3.36=6.72
=6.72÷3.36
=2
(2)=
解:8=20×15
8=300
=300÷8
=37.5
(3)12∶(-2)=1∶
解:(-2)×1=12×
-2=8
=8+2
=10
18.(1)见详解
(2)圆锥;339.12
(1)把图形A按照3∶1放大,就是将图形A的底和高放大到原来的3倍,放大后图形与原图形对应边长的比是3∶1,形状没有发生变化。
(2)如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个圆锥,圆锥的高是较长的直角边,底面半径是较短的直角边,根据圆锥的体积:V=πr2h,代入数据计算即可。
(1)底:2×3=6(厘米)
高:3×3=9(厘米)
作图如下:
(2)×62×3.14×9
=×36×3.14×9
=339.12(立方厘米)
如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个圆锥,这个图形的体积是339.12立方厘米。
19.(1)介休三中;政务中心。
(2)15;13
(3)28元
(1)正数与负数表示意义相反的两种量,规定上车人数记为正,则和它意义相反的下车人数就为负,无人上车和下车记为0。
(2)用火车站北、定阳饭店、政务中心、介休三中的上车人数,减去下车的人数即可知道这辆公交车从介休三中站开出时,车上的乘客人数;同理计算出从北坛公园东站开出时,车上的乘客人数。
(3)计算出从火车站北到北坛公园东站所有的上车总人数,再乘1(票价为1元),即可求出收入总钱数。
(1)从火车站到北坛公园东站,途中无人上车的站是介休三中,无人下车的站是政务中心。
(2)9+7+6-3-4=15(人)
15+5+1-3-5=13(人)
这辆公交车从介休三中站开出时,车上有15名乘客,从北坛公园东站开出时,车上有13名乘客。
(3)(9+7+6+5+1)×1
=28×1
=28(元)
答:已经收入28元。
20.(1)见详解
(2)正
(3)6.4米;5米
(1)根据统计图提供的数据,绘制统计图。
(2)成正比例的量,图像是一条射线;成反比例的量,图像是一条曲线;据此解答。
(3)再根据图像,找出与树高8米对应的点,找出与影长4米对应的点即可。
(1)如图:
(2)连线以后观察,可以发现:影长与树高成正比例。
(3)根据图像可知,树高8米时,影长是6.4米,
影长4米时,树高5米。
答:树高8米时,影长6.4米,影长4米时,树高5米。
21.6000本
现在的书比原来多了二成,就是现在的书比原来多了20%,也就是以原来的书数量为单位“1”,增加了原来的20%,求一个数的百分之几用乘法就是得出增加的本数再加上原来书的本数就是现在书的本数。
5000+5000×20%
=5000+1000
=6000(本)
答:现在有图书6000本。
22.6杯
分析题目,用S表示瓶底和圆锥形杯口的面积,瓶子中液体的高是(h+h),根据圆柱的体积=底面积×高,圆锥的体积(容积)=底面积×高×,分别求出瓶子中液体的体积和圆锥形杯子的容积,再用液体的体积除以圆锥形杯子的容积即可解答。
设瓶底和圆锥形杯口的面积为S,瓶子中液体的高是(h+h),圆锥形杯子的高为h。
瓶子中液体的体积:S×(h+h)=S×2h=2Sh
圆锥形杯子的容积:S×h×=Sh
2Sh÷(Sh)
=2÷
=2×3
=6(杯)
答:通过计算可知,将瓶子中的液体倒入圆锥形杯子中,能倒满6杯。
23.2.4厘米
根据比例尺=图上距离∶实际距离,1厘米=10毫米,根据进率统一单位后,先用近似长方形细胞在显微镜下的宽∶近似长方形细胞的宽,求出放大镜的比例尺,再根据图上距离=实际距离×比例尺,代入数据,求出这个细胞在显微镜下的长度,注意单位名数的换算。
0.1毫米=0.01厘米;0.12毫米=0.012厘米
2∶0.01
=(2×100)∶(0.01×100)
=200∶1
0.012×200=2.4(厘米)
答:这个细胞在显微镜下的长是2.4厘米。
24.127.17米
根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形沙堆的体积;
把铺的路面看作一个长方体,求铺的长度,就是求长方体的长,圆锥形沙堆的体积等于长方体的体积;已知长方体的宽是10米,高是2厘米,求长,用圆锥形沙堆的体积÷(宽×高),代入数据,即可求出铺的长度,注意单位名数的统一。
2厘米=0.02米
28.26×2.7×÷(10×0.02)
=28.26×2.7×÷0.2
=76.302×÷0.2
=25.434÷0.2
=127.17(米)
答:能铺127.17米。
25.(1)420千米
(2)1∶3000000
(1)根据长度测量方法,测量出大同到介休的图上距离,根据实际距离=图上距离÷比例尺,进行换算即可。
(2)图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可。
(1)测量可知大同到介休的图上距离是3厘米。
3÷=3×14000000=42000000(厘米)=420(千米)
答:大同到介休的实际距离是420千米。
(2)14厘米∶42000000厘米=(14÷14)∶(42000000÷14)=1∶3000000
答:这幅地图的比例尺是1∶3000000。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中综合试卷
2024--2025学年小学数学人教版六年级下册
一、选择题
1.下面各选项中的两种量成反比例的是( )。
A.圆的半径和面积。 B.李师傅8小时做的零件个数和工作效率。
C.从介休到太原,汽车行驶的时间和速度。 D.小栋的身高和他的体重。
2.解决图中的问题,列式正确的是( )。
A.180×(1-20%) B.180÷(1-20%) C.180×(1+20%) D.180÷(1+20%)
3.下面使用转化思想解决问题的是( )。
A.①② B.①②③ C.②③④ D.①②③④
4.圆锥的侧面展开图的形状是( )。
A.扇形 B.圆形 C.三角形 D.等腰三角形
5.按下面的程序操作,输入的数a与计算结果b之间的关系是怎样的?( )
输入a(不为0的自然数) → → → 输出计算结果b
A.a与b成正比例关系 B.a与b成反比例关系
C.a与b不成比例 D.无法判断a与b是否成比例
6.小明发现他的铅笔头是圆锥形,笔杆是圆柱形,且圆柱的长是圆锥的3倍,那么圆柱的体积是圆锥的( )倍。
A.3 B.6 C.9 D.27
二、填空题
7.在﹣6、3、0、﹣18、﹢7中,( )是正数,( )是负数,( )既不是正数,也不是负数。
8.一个圆柱的体积是80cm3,底面积是16cm2。它的高是( )厘米。
9.小兰去学校时向东走500米,返回时应向( )行走( )米。
10.一本课外书,原价40元,现在按八五折优惠销售,比原价便宜了( )元。
11.在一个比例里,两外项互为倒数,一个内项是0.8,另一个内项是( )。
12.在一幅地图上量得两地间的距离是3cm,已知两地的实际距离是15km,这幅地图的比例尺是( );在比例尺为1∶2000的地图上,6cm的线段代表实际距离( )m,实际距离180m在图上要画( )cm。
13.一个圆柱的底面半径是3cm,高是10cm,它的侧面积是( )体积是( )。
14.一个圆锥的体积是75.36cm3,这个圆锥的底面直径是6cm,高是( )cm,和它等底等高的圆柱的体积是( )cm3。
三、计算题
15.直接写出下列各题的得数。
×= 47×20%= 2÷-÷2=
300÷5%= 0.42-0.43= 3r×6r=
16.怎样算简便就怎样算。
9.6-117%-5.83+11.4 (1.68+1.68+1.68+1.68)×2.5
3.1÷+3.1×20% 9×(-)×15 2025÷12.5%÷8
17.解比例。
3.36∶2.8=2.4∶ = 12∶(-2)=1∶
四、作图题
18.下面每个小正方形的边长表示1厘米。
(1)画出图形A按3∶1放大后得到的图形B。
(2)如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个( ),这个图形的体积是( )立方厘米。
五、解答题
19.介休103路内环公交车从起点站(火车站)开出,下面是它经过几个停靠站时上下车人数的记录表。(上车人数记为正)
车站名 火车站北 定阳饭店 政务中心 介休三中 介纺社区 北坛公园东
上车人数 ﹢9 ﹢7 ﹢6 0 ﹢5 ﹢1
下车人数 ﹣ ﹣3 0 ﹣4 ﹣3 ﹣5
(1)从火车站到北坛公园东站,途中无人上车的站是__________,无人下车的站是__________。
(2)这辆公交车从介休三中站开出时,车上有( )名乘客,从北坛公园东站开出时,车上有( )名乘客。
(3)介休103路所有乘客统一票价为1元,那么这趟公交车从北坛公园东站开出时,已经收入多少钱?
20.成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速”。用数学的眼光看该成语,是应用了比例的知识。
如表所示为同一时间、同一地点测得的树高和影长。
树高/m 2 3 4 6
影长/m 1.6 2.4 3.2 4.8
(1)在图中描出表示树高和对应影长的点,然后把它们连起来。
(2)连线以后观察,可以发现:影长与树高成( )比例关系。
(3)利用图像判断,树高8米时,影长多少米?影长4米时,树高多少米?
21.蒲公英图书馆原有5000本书,后又新增了一批图书,现在的书比原来多了二成,现在有图书多少本?(先画图分析,然后列式解答出来。)
22.如图,瓶底的面积和圆锥形杯口的面积相等,将瓶子中的液体倒入圆锥形杯子中,能倒满几杯?(忽略瓶壁和杯壁的厚度)请把你的想法简洁地表达在下面。
23.显微镜是主要用于放大微小物体为人的肉眼所能看到的仪器。一个长为0.12毫米,宽为0.1毫米的近似长方形的细胞。在显微镜下的宽是2厘米,那么这个细胞在显微镜下的长是多少厘米?
24.一个圆锥形沙堆,底面积28.26平方米,高是2.7米。用这堆沙在10米宽的公路上铺2厘米厚的路面,能铺多少米?
25.“五一”快到了,聪聪一家计划开车从大同到介休旅游。
(1)根据地图请你计算大同到介休的实际距离是多少千米?(图上距离取整厘米)
(2)在另一幅地图上量得大同与介休的图上距离是14厘米,这幅地图的比例尺是多少?
参考答案
1.C
相关的两个量,如果它们的商一定,那么它们成正比例;如果它们的乘积一定,那么它们成反比例,据此逐项分析解答。
A.因为圆的面积÷半径=π×半径,π×半径随着半径的变化而变化,所以圆的面积和半径不成反比例关系;
B.李师傅工作8小时,零件总数÷工作效率=8小时(定值),零件总数与工作效率的商一定,而反比例关系要求两个量的乘积一定。所以李师傅8小时做的零件个数和工作效率不成反比例;
C.因为速度×时间=路程,从介休到太原两地路程一定,所以汽车行驶的速度和时间成反比例;
D.因为身高和体重会受到很多因素的影响,两者并没有严格的数学比例关系,所以小栋的身高和他的体重不成比例。
故答案为:C
2.D
以2023的产值为单位“1”,二成=20%,已知2024年的产值(180万元)相当于2023年的1+20%=120%,根据已知比一个数多百分之几是多少,求这个数用除法计算。用2024年的产值÷120%即可。
180÷(1+20%)
=180÷120%
=150(万元)
2023的产值为150万元。
故答案为:D
3.D
① 把圆柱的体积转化为长方体,利用长方体体积公式,推导出圆柱的体积公式,用了转化思想解决问题。
②把圆柱的侧面积转化为长方形,利用长方形面积公式,推导出圆柱的侧面积公式,用了转化思想解决问题。
③把瓶子中的液体转化为两个圆柱的容积,求出瓶子的容积,用了转化思想解决问题。
④把不规则物体的体积转化为圆柱的体积,求出不规则物体的体积,用了转化思想解决问题。据此解答。
根据分析可知,使用转化思想解决问题的是①②③④。
故答案为:D
4.A
圆锥的底面圆和侧面组成,侧面是连接底面圆周与顶点的曲面;将圆锥的侧面沿一条母线(从顶点到底面圆周的线段),剪开并摊平,曲面变为平面。展开后母线成为扇形的半径,底面圆的周长对应扇形的弧长,据此解答。
根据分析可知,圆锥的侧面展开图的形状是扇形。
故答案为:A
5.A
程序操作可得:a××=b。判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。据此判断即可。
a××=b可得:b÷a=×=
因为比值一定,所以a和b成正比例关系。
故答案为:A
6.C
圆锥和圆柱的底面半径相同,可以设为r,圆锥的高为,圆柱的高是圆锥的3倍,则圆柱的高为3h。分别根据圆柱的体积和圆锥的体积得出体积得出两个图形之间的关系。
设半径为r,圆锥的高为,圆柱的高为3h。
圆柱:
圆锥:
则圆柱的体积是圆锥的9倍。
故答案为:C
7. 3,﹢7 ﹣6,﹣18 0
根据正、负数的意义,大于0的数是正数,正数的前面有“﹢”号,也可以省略前面的“﹢”号;小于0的数是负数,负数的前面有“﹣”号,0既不是正数也不是负数,据此判断即可。
正数:3,﹢7;
负数:﹣6,﹣18。
在﹣6、3、0、﹣18、﹢7中,3,﹢7是正数,﹣6,﹣18是负数,0既不是正数,也不是负数。
8.5
圆柱体积=底面积×高,据此求解。
80÷16=5(cm),所以这个圆柱的高是5cm。
掌握圆柱的体积公式是解决本题的关键。
9. 西 500
规定某个方向为正,则相反方向即为负。
小兰去学校时向东走了500米,返回时应向相反的方向西走相同的距离500米。
10.6
打八五折,就是按原价的85%销售,便宜了1-85%,用原价×便宜的对应百分率即可。
40×(1-85%)
=40×0.15
=6(元)
比原价便宜了6元。
本题考查了百分数实际应用题,打折销售是商家常用的促销手段。
11.1.25//
互为倒数的两个数乘积为1,据此可知比例的外项之积是1,再根据比例的基本性质:两内项之积等于两外项之积可知两内项之积也等于1,据此用1除以一个内项即可得到另一个内项。
1÷0.8=1.25
在一个比例里,两外项互为倒数,一个内项是0.8,另一个内项是1.25。
12. 1∶500000/ 120 9
(1)先根据1km=100000cm把15km化成以cm为单位,再根据比例尺=图上距离∶实际距离求出比例尺即可;
(2)先根据实际距离=图上距离÷比例尺求出实际距离,再根据1m=100cm把结果换算成以m为单位即可;
(3)先根据1m=100cm把180m换算成以cm为单位,再根据图上距离=实际距离×比例尺求出图上距离即可。
15km=1500000cm
3cm∶1500000cm
=3∶1500000
=(3÷3)∶(1500000÷3)
=1∶500000
6÷=6×2000=12000(cm)
12000cm=120m
180m=18000cm
18000×=9(cm)
在一幅地图上量得两地间的距离是3cm,已知两地的实际距离是15km,这幅地图的比例尺是1∶500000;在比例尺为1∶2000的地图上,6cm的线段代表实际距离120m,实际距离180m在图上要画9cm。
13. 188.4 282.6
圆柱的侧面积S=Ch=2πrh;圆柱的体积V=Sh=πr2h;据此代入数据计算即可。
侧面积:3.14×3×2×10=188.4(cm2)
体积:3.14×32×10=282.6(cm3)
故答案为:188.4;282.6
本题主要考查圆柱的侧面积及体积的公式,牢记公式是解题的关键,解题时要细心。
14. 8 226.08
圆锥的高=圆锥的体积÷÷底面积,即可解答;圆锥体积是和它等底等高的圆柱的体积的,据此解答。
圆锥的高:
75.36÷÷[3.14×(6÷2)2]
=75.36×3÷28.26
=226.08÷28.26
=8(cm)
和它等底等高的圆柱的体积是:
75.36÷
=75.36×3
=226.08(cm3)
本题考查了圆锥高的求法以及已知圆锥体积求和它等底等高的圆柱的体积的方法,注意认真计算牢记公式。
15.;9.4;
6000;0.096;18r2
略
16.14;16.8
3.1;42;2025
(1)根据加法的交换律和结合律、减法的性质,将原式变成(9.6+11.4)-(117%+5.83),即可简算。
(2)根据乘法的意义,将原式变成1.68×4×2.5,再根据乘法的结合律,将算式变成1.68×(4×2.5),即可简算。
(3)先将原式变成3.1×+3.1×,再根据乘法分配律,将算式变成3.1×(+),即可简算。
(4)根据乘法交换律将原式变成9×15×(-),再根据乘法分配律,将算式变成9×15×-9×15×,即可简算。
(5)根据除法的性质,将原式变成2025÷(12.5%×8),即可简算。
9.6-117%-5.83+11.4
=(9.6+11.4)-(117%+5.83)
=21-7
=14
(1.68+1.68+1.68+1.68)×2.5
=1.68×4×2.5
=1.68×(4×2.5)
=1.68×10
=16.8
3.1÷+3.1×20%
=3.1×+3.1×
=3.1×(+)
=3.1×1
=3.1
9×(-)×15
=9×15×(-)
=9×15×-9×15×
=60-18
=42
2025÷12.5%÷8
=2025÷(12.5%×8)
=2025÷1
=2025
17.=2;=37.5;=10
(1)先根据比例的基本性质将比例方程改写成3.36=2.8×2.4,然后方程两边同时除以3.36,求出方程的解;
(2)先根据比例的基本性质将比例方程改写成8=20×15,然后方程两边同时除以8,求出方程的解;
(3)先根据比例的基本性质将比例方程改写成(-2)×1=12×,然后把方程化简成-2=8,方程两边再同时加上2,求出方程的解。
(1)3.36∶2.8=2.4∶
解:3.36=2.8×2.4
3.36=6.72
=6.72÷3.36
=2
(2)=
解:8=20×15
8=300
=300÷8
=37.5
(3)12∶(-2)=1∶
解:(-2)×1=12×
-2=8
=8+2
=10
18.(1)见详解
(2)圆锥;339.12
(1)把图形A按照3∶1放大,就是将图形A的底和高放大到原来的3倍,放大后图形与原图形对应边长的比是3∶1,形状没有发生变化。
(2)如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个圆锥,圆锥的高是较长的直角边,底面半径是较短的直角边,根据圆锥的体积:V=πr2h,代入数据计算即可。
(1)底:2×3=6(厘米)
高:3×3=9(厘米)
作图如下:
(2)×62×3.14×9
=×36×3.14×9
=339.12(立方厘米)
如果以图形B的一条较长的直角边所在直线为轴旋转一周,那么会形成一个圆锥,这个图形的体积是339.12立方厘米。
19.(1)介休三中;政务中心。
(2)15;13
(3)28元
(1)正数与负数表示意义相反的两种量,规定上车人数记为正,则和它意义相反的下车人数就为负,无人上车和下车记为0。
(2)用火车站北、定阳饭店、政务中心、介休三中的上车人数,减去下车的人数即可知道这辆公交车从介休三中站开出时,车上的乘客人数;同理计算出从北坛公园东站开出时,车上的乘客人数。
(3)计算出从火车站北到北坛公园东站所有的上车总人数,再乘1(票价为1元),即可求出收入总钱数。
(1)从火车站到北坛公园东站,途中无人上车的站是介休三中,无人下车的站是政务中心。
(2)9+7+6-3-4=15(人)
15+5+1-3-5=13(人)
这辆公交车从介休三中站开出时,车上有15名乘客,从北坛公园东站开出时,车上有13名乘客。
(3)(9+7+6+5+1)×1
=28×1
=28(元)
答:已经收入28元。
20.(1)见详解
(2)正
(3)6.4米;5米
(1)根据统计图提供的数据,绘制统计图。
(2)成正比例的量,图像是一条射线;成反比例的量,图像是一条曲线;据此解答。
(3)再根据图像,找出与树高8米对应的点,找出与影长4米对应的点即可。
(1)如图:
(2)连线以后观察,可以发现:影长与树高成正比例。
(3)根据图像可知,树高8米时,影长是6.4米,
影长4米时,树高5米。
答:树高8米时,影长6.4米,影长4米时,树高5米。
21.6000本
现在的书比原来多了二成,就是现在的书比原来多了20%,也就是以原来的书数量为单位“1”,增加了原来的20%,求一个数的百分之几用乘法就是得出增加的本数再加上原来书的本数就是现在书的本数。
5000+5000×20%
=5000+1000
=6000(本)
答:现在有图书6000本。
22.6杯
分析题目,用S表示瓶底和圆锥形杯口的面积,瓶子中液体的高是(h+h),根据圆柱的体积=底面积×高,圆锥的体积(容积)=底面积×高×,分别求出瓶子中液体的体积和圆锥形杯子的容积,再用液体的体积除以圆锥形杯子的容积即可解答。
设瓶底和圆锥形杯口的面积为S,瓶子中液体的高是(h+h),圆锥形杯子的高为h。
瓶子中液体的体积:S×(h+h)=S×2h=2Sh
圆锥形杯子的容积:S×h×=Sh
2Sh÷(Sh)
=2÷
=2×3
=6(杯)
答:通过计算可知,将瓶子中的液体倒入圆锥形杯子中,能倒满6杯。
23.2.4厘米
根据比例尺=图上距离∶实际距离,1厘米=10毫米,根据进率统一单位后,先用近似长方形细胞在显微镜下的宽∶近似长方形细胞的宽,求出放大镜的比例尺,再根据图上距离=实际距离×比例尺,代入数据,求出这个细胞在显微镜下的长度,注意单位名数的换算。
0.1毫米=0.01厘米;0.12毫米=0.012厘米
2∶0.01
=(2×100)∶(0.01×100)
=200∶1
0.012×200=2.4(厘米)
答:这个细胞在显微镜下的长是2.4厘米。
24.127.17米
根据圆锥的体积公式:体积=底面积×高×,代入数据,求出圆锥形沙堆的体积;
把铺的路面看作一个长方体,求铺的长度,就是求长方体的长,圆锥形沙堆的体积等于长方体的体积;已知长方体的宽是10米,高是2厘米,求长,用圆锥形沙堆的体积÷(宽×高),代入数据,即可求出铺的长度,注意单位名数的统一。
2厘米=0.02米
28.26×2.7×÷(10×0.02)
=28.26×2.7×÷0.2
=76.302×÷0.2
=25.434÷0.2
=127.17(米)
答:能铺127.17米。
25.(1)420千米
(2)1∶3000000
(1)根据长度测量方法,测量出大同到介休的图上距离,根据实际距离=图上距离÷比例尺,进行换算即可。
(2)图上距离∶实际距离=比例尺,据此写出图上距离与实际距离的比,化简即可。
(1)测量可知大同到介休的图上距离是3厘米。
3÷=3×14000000=42000000(厘米)=420(千米)
答:大同到介休的实际距离是420千米。
(2)14厘米∶42000000厘米=(14÷14)∶(42000000÷14)=1∶3000000
答:这幅地图的比例尺是1∶3000000。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
