湖北省武汉市部分学校2024-2025学年四调九年级数学模拟试题(含答案)
文档属性
| 名称 | 湖北省武汉市部分学校2024-2025学年四调九年级数学模拟试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 23:03:15 | ||
图片预览


文档简介
武汉市部分学校2024~2025学年四调九年级数学试题(4.23)
数学试卷
一、选择题:(本大题共10小题,每小题3分,共30分)
1.纹样是我国古代艺术的瑰宝,下列图形中不是中心对称图形的是( )
A B C D
2.袋子中装有3个白球,1个红球.从中一次性取出2个球,下列事件是必然事件的是( )
A.两个球都是白球 B.两个球都是红球
C.两个球中至少有一个白球 D.两个球中至少有一个红球
3.如图是一个水平放置的圆柱体,关于该几何体的三视图描述正确的是( )
A.主视图和左视图相同 B.主视图和俯视图相同
C.左视图和俯视图相同 D.三个视图都不相同.
4.截至2024年12月底,国家铁路局最新数据显示,我国铁路运营里程约162 000 km.将数据162 000用科学记数法表示是( )
A.0.162×105 B.0.162×106 C.1.62×105 D.1.62×106
5.计算(2x2)3的结果是( )
A.2x5 B.6x5 C.6x6 D.8x6
6.把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
7.某校课后服务期间开展足球、篮球,排球,羽毛球四项球类活动,小美和小好两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
8.小美骑车从学校回家,中途在文具店停留了2 min,然后继续骑车回家.若小美骑车的速度始终不变.从出发开始计时,小美离家的路程s(单位:m)与时间t(单位:min)的对应关系如图所示,则从文具店到小美家的路程是( )
A.550 m B.500 m C.450 m D.400 m
9.如图,在 Rt△ABC中,∠ACB=90°,AC=5,BC=12,⊙O是△ABC的内切圆,连接OA,OB,则图中阴影部分的面积是( )
A.π B.π C.π D.π
10.小美在学习完《多边形内角和》后,做一个剪纸片的游戏:有一张三角形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片;从这3张中任选一张,重复上述操作,得到4张纸片;…,如此下去.若最后得到8张纸片,其中有4张三角形纸片,2张四边形纸片,1张五边形纸片,则还有1张多边形纸片的边数是( )
A.6 B.7 C.8 D.9
二、填空题:(本大题共6小题,每小题3分,共18分)
11.我国古代数学著作《九章算术》中提出了正数,负数的概念.若水库的水位升高2 m时,水位变化记作+2 m,则水库的水位下降1 m时,水位变化记作 m.
12.已知蓄电池的电压U(单位:V)为定值,使用蓄电池时,电流I单位:A)与电阻R(单位:Q)的函数关系是I=,.若电阻为9Q时,电流为4A,则蓄电池的电压是 V.
13.计算-的结果是 .
14.如图,建筑物BC上有一旗杆,从与BC相距40 m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度是 m.(参考数据:tan50=1.192.)
15.如图,在Rt △ABC中,∠ACB=90°,tanA=,AB=48,D,E分别在AC和 BC上,将△CDE沿DE折叠,点C的对应点F恰好落在AB上.若△DEF与△ABC相似,则DE的长是 .
16.在学习了“利用函数的图象研究函数”后,为了研究函数y=的性质,小美用描点法画它的图象,列出了如下表格:
x … -3 -2 -1 0 1 2 3 …
y= … 1 …
下列五个结论:
①点(5,)在该函数图象上;②该函数图象在x轴上方;③该函数图象有最高点;
④若A(π,y1)和B(-,y2)是该函数图象上两点,则y2>y1;
⑤若将该函数图象向左平移1个单位长度,则平移后的图象的函数解析式是y=.
其中正确的结论是 (填写序号).
三、解答题:(共8小题,共72分)
17.(本小题满分8分)解不等式组
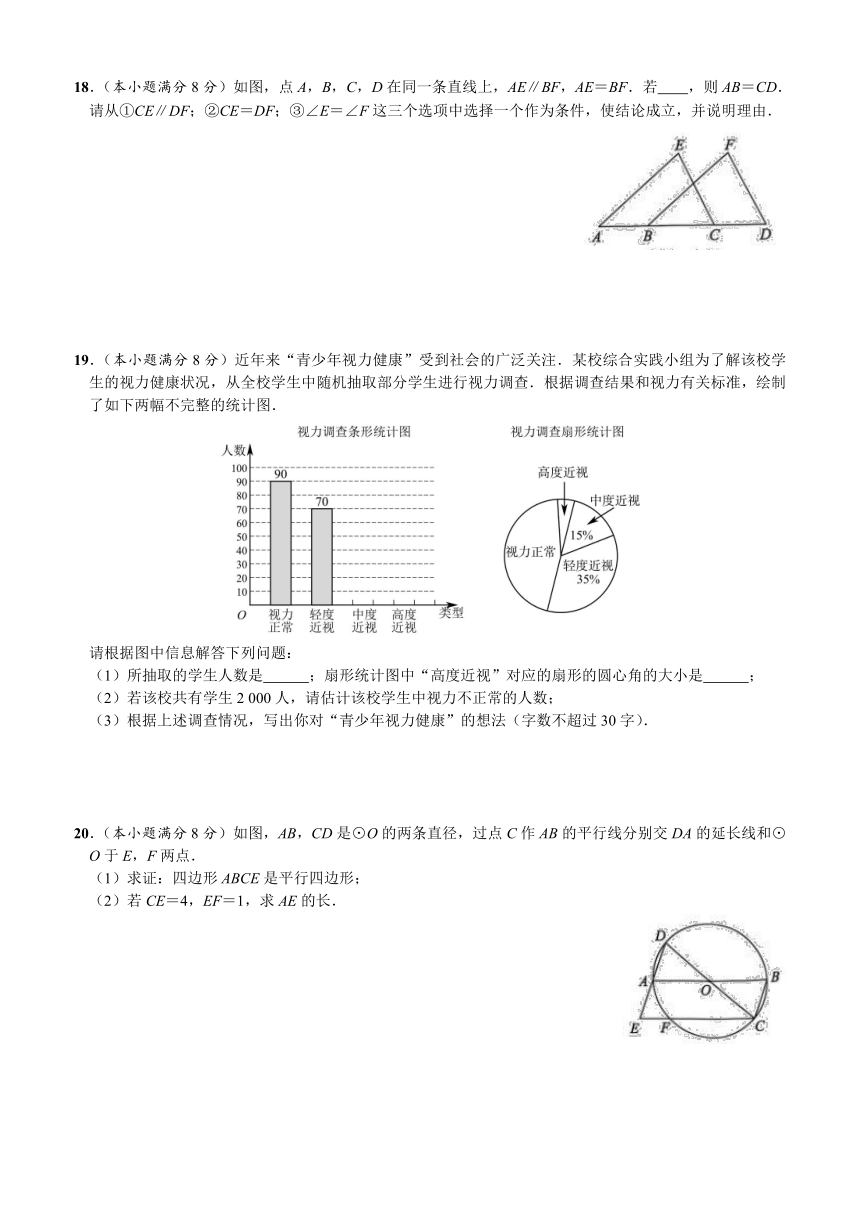
18.(本小题满分8分)如图,点A,B,C,D在同一条直线上,AE∥BF,AE=BF.若 ,则AB=CD.
请从①CE∥DF;②CE=DF;③∠E=∠F这三个选项中选择一个作为条件,使结论成立,并说明理由.
19.(本小题满分8分)近年来“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了如下两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)所抽取的学生人数是 ;扇形统计图中“高度近视”对应的扇形的圆心角的大小是 ;
(2)若该校共有学生2 000人,请估计该校学生中视力不正常的人数;
(3)根据上述调查情况,写出你对“青少年视力健康”的想法(字数不超过30字).
20.(本小题满分8分)如图,AB,CD是⊙O的两条直径,过点C作AB的平行线分别交DA的延长线和⊙O于E,F两点.
(1)求证:四边形ABCE是平行四边形;
(2)若CE=4,EF=1,求AE的长.
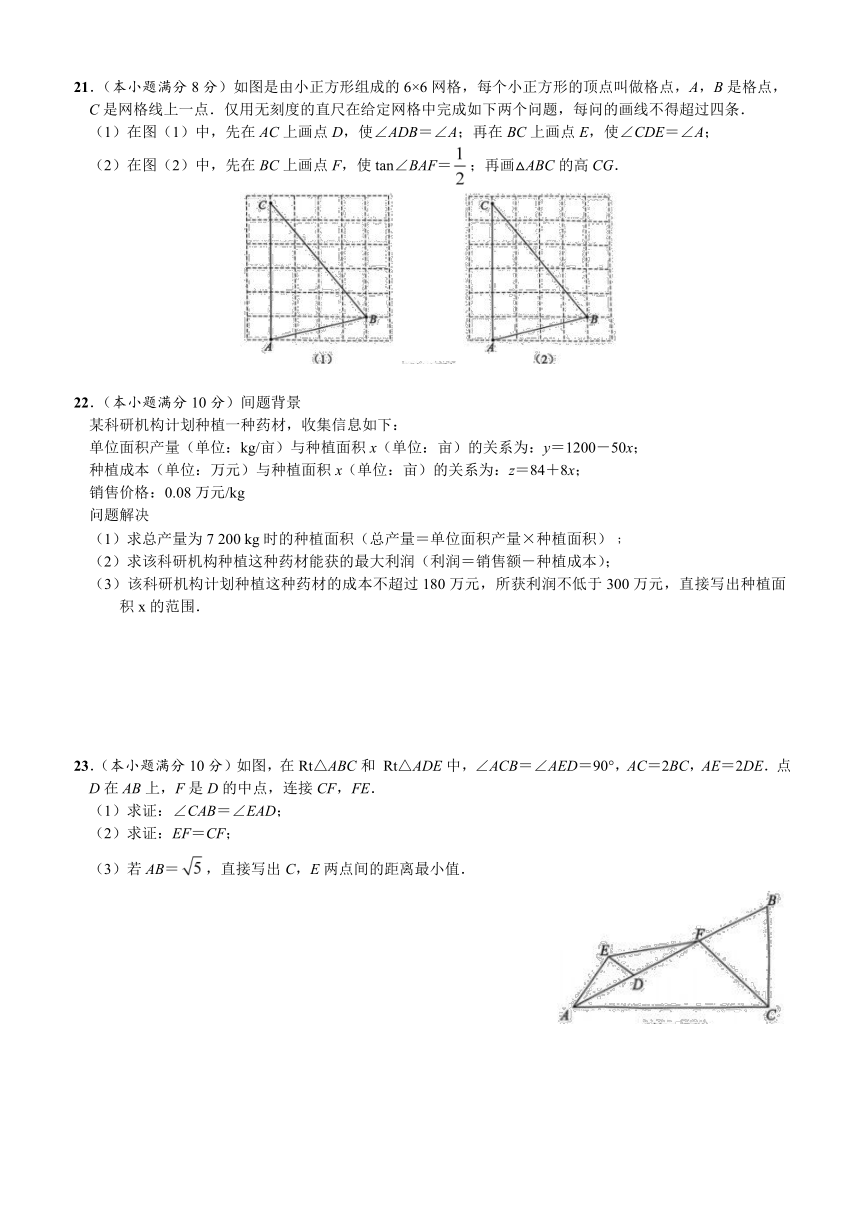
21.(本小题满分8分)如图是由小正方形组成的6×6网格,每个小正方形的顶点叫做格点,A,B是格点,C是网格线上一点.仅用无刻度的直尺在给定网格中完成如下两个问题,每问的画线不得超过四条.
(1)在图(1)中,先在AC上画点D,使∠ADB=∠A;再在BC上画点E,使∠CDE=∠A;
(2)在图(2)中,先在BC上画点F,使tan∠BAF=;再画△ABC的高CG.
22.(本小题满分10分)间题背景
某科研机构计划种植一种药材,收集信息如下:
单位面积产量(单位:kg/亩)与种植面积x(单位:亩)的关系为:y=1200-50x;
种植成本(单位:万元)与种植面积x(单位:亩)的关系为:z=84+8x;
销售价格:0.08万元/kg
问题解决
(1)求总产量为7 200 kg时的种植面积(总产量=单位面积产量×种植面积)﹔
(2)求该科研机构种植这种药材能获的最大利润(利润=销售额-种植成本);
(3)该科研机构计划种植这种药材的成本不超过180万元,所获利润不低于300万元,直接写出种植面积x的范围.
23.(本小题满分10分)如图,在Rt△ABC和 Rt△ADE中,∠ACB=∠AED=90°,AC=2BC,AE=2DE.点D在AB上,F是D的中点,连接CF,FE.
(1)求证:∠CAB=∠EAD;
(2)求证:EF=CF;
(3)若AB=,直接写出C,E两点间的距离最小值.
24.(本小题满分12分)如图(1),抛物线y=x2-x-3交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
答案
数学试卷
一、选择题:(本大题共10小题,每小题3分,共30分)
1.纹样是我国古代艺术的瑰宝,下列图形中不是中心对称图形的是( )
A B C D
2.袋子中装有3个白球,1个红球.从中一次性取出2个球,下列事件是必然事件的是( )
A.两个球都是白球 B.两个球都是红球
C.两个球中至少有一个白球 D.两个球中至少有一个红球
3.如图是一个水平放置的圆柱体,关于该几何体的三视图描述正确的是( )
A.主视图和左视图相同 B.主视图和俯视图相同
C.左视图和俯视图相同 D.三个视图都不相同.
4.截至2024年12月底,国家铁路局最新数据显示,我国铁路运营里程约162 000 km.将数据162 000用科学记数法表示是( )
A.0.162×105 B.0.162×106 C.1.62×105 D.1.62×106
5.计算(2x2)3的结果是( )
A.2x5 B.6x5 C.6x6 D.8x6
6.把一块含30°角的直角三角板按如图方式放置在两条平行线之间,若∠1=54°,则∠2的大小是( )
A.26° B.24° C.22° D.20°
7.某校课后服务期间开展足球、篮球,排球,羽毛球四项球类活动,小美和小好两位同学各自任选其中一项参加,则他们选择同一项活动的概率是( )
A. B. C. D.
8.小美骑车从学校回家,中途在文具店停留了2 min,然后继续骑车回家.若小美骑车的速度始终不变.从出发开始计时,小美离家的路程s(单位:m)与时间t(单位:min)的对应关系如图所示,则从文具店到小美家的路程是( )
A.550 m B.500 m C.450 m D.400 m
9.如图,在 Rt△ABC中,∠ACB=90°,AC=5,BC=12,⊙O是△ABC的内切圆,连接OA,OB,则图中阴影部分的面积是( )
A.π B.π C.π D.π
10.小美在学习完《多边形内角和》后,做一个剪纸片的游戏:有一张三角形的纸片,用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片;从这2张中任选一张,再用剪刀沿一条不过任何顶点的直线将其剪成了2张纸片,这样共有3张纸片;从这3张中任选一张,重复上述操作,得到4张纸片;…,如此下去.若最后得到8张纸片,其中有4张三角形纸片,2张四边形纸片,1张五边形纸片,则还有1张多边形纸片的边数是( )
A.6 B.7 C.8 D.9
二、填空题:(本大题共6小题,每小题3分,共18分)
11.我国古代数学著作《九章算术》中提出了正数,负数的概念.若水库的水位升高2 m时,水位变化记作+2 m,则水库的水位下降1 m时,水位变化记作 m.
12.已知蓄电池的电压U(单位:V)为定值,使用蓄电池时,电流I单位:A)与电阻R(单位:Q)的函数关系是I=,.若电阻为9Q时,电流为4A,则蓄电池的电压是 V.
13.计算-的结果是 .
14.如图,建筑物BC上有一旗杆,从与BC相距40 m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度是 m.(参考数据:tan50=1.192.)
15.如图,在Rt △ABC中,∠ACB=90°,tanA=,AB=48,D,E分别在AC和 BC上,将△CDE沿DE折叠,点C的对应点F恰好落在AB上.若△DEF与△ABC相似,则DE的长是 .
16.在学习了“利用函数的图象研究函数”后,为了研究函数y=的性质,小美用描点法画它的图象,列出了如下表格:
x … -3 -2 -1 0 1 2 3 …
y= … 1 …
下列五个结论:
①点(5,)在该函数图象上;②该函数图象在x轴上方;③该函数图象有最高点;
④若A(π,y1)和B(-,y2)是该函数图象上两点,则y2>y1;
⑤若将该函数图象向左平移1个单位长度,则平移后的图象的函数解析式是y=.
其中正确的结论是 (填写序号).
三、解答题:(共8小题,共72分)
17.(本小题满分8分)解不等式组
18.(本小题满分8分)如图,点A,B,C,D在同一条直线上,AE∥BF,AE=BF.若 ,则AB=CD.
请从①CE∥DF;②CE=DF;③∠E=∠F这三个选项中选择一个作为条件,使结论成立,并说明理由.
19.(本小题满分8分)近年来“青少年视力健康”受到社会的广泛关注.某校综合实践小组为了解该校学生的视力健康状况,从全校学生中随机抽取部分学生进行视力调查.根据调查结果和视力有关标准,绘制了如下两幅不完整的统计图.
请根据图中信息解答下列问题:
(1)所抽取的学生人数是 ;扇形统计图中“高度近视”对应的扇形的圆心角的大小是 ;
(2)若该校共有学生2 000人,请估计该校学生中视力不正常的人数;
(3)根据上述调查情况,写出你对“青少年视力健康”的想法(字数不超过30字).
20.(本小题满分8分)如图,AB,CD是⊙O的两条直径,过点C作AB的平行线分别交DA的延长线和⊙O于E,F两点.
(1)求证:四边形ABCE是平行四边形;
(2)若CE=4,EF=1,求AE的长.
21.(本小题满分8分)如图是由小正方形组成的6×6网格,每个小正方形的顶点叫做格点,A,B是格点,C是网格线上一点.仅用无刻度的直尺在给定网格中完成如下两个问题,每问的画线不得超过四条.
(1)在图(1)中,先在AC上画点D,使∠ADB=∠A;再在BC上画点E,使∠CDE=∠A;
(2)在图(2)中,先在BC上画点F,使tan∠BAF=;再画△ABC的高CG.
22.(本小题满分10分)间题背景
某科研机构计划种植一种药材,收集信息如下:
单位面积产量(单位:kg/亩)与种植面积x(单位:亩)的关系为:y=1200-50x;
种植成本(单位:万元)与种植面积x(单位:亩)的关系为:z=84+8x;
销售价格:0.08万元/kg
问题解决
(1)求总产量为7 200 kg时的种植面积(总产量=单位面积产量×种植面积)﹔
(2)求该科研机构种植这种药材能获的最大利润(利润=销售额-种植成本);
(3)该科研机构计划种植这种药材的成本不超过180万元,所获利润不低于300万元,直接写出种植面积x的范围.
23.(本小题满分10分)如图,在Rt△ABC和 Rt△ADE中,∠ACB=∠AED=90°,AC=2BC,AE=2DE.点D在AB上,F是D的中点,连接CF,FE.
(1)求证:∠CAB=∠EAD;
(2)求证:EF=CF;
(3)若AB=,直接写出C,E两点间的距离最小值.
24.(本小题满分12分)如图(1),抛物线y=x2-x-3交x轴于A,B两点(点A在左边),交y轴于点C.
(1)直接写出A,B,C三点的坐标;
(2)D是抛物线第四象限上的一点,连接AD分别交BC,OC于E,F两点,若∠FEC=∠FCE,求直线AD的解析式;
(3)平移抛物线使它的顶点为(0,1),如图(2).R是y轴上一个定点,以点R为直角顶点作Rt△RST,使顶点S,T分别在x轴和抛物线上.若Rt△RST在变化的过程中,直线ST与抛物线始终有唯一公共点,求点R的坐标.
答案
同课章节目录
