4.4用待定系数法确定一次函数表示式 教案
文档属性
| 名称 | 4.4用待定系数法确定一次函数表示式 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 226.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-24 19:53:42 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第6课时《4.4用待定系数法确定一次函数表示式 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 充分让学生合作探究,培养学生自主学习的能力,增进学生之间的友谊.
学习者分析 数形结合思想和归纳总结能力.
教学目标 待定系数法求一次函数的解析式。体会二元一次方程组的应用.
教学重点 让学生能在不同的条件下运用待定系数法求出一次函数的解析式 .
教学难点 用待定系数法求一次函数的解析式,渗透数形结合思想和归纳总结能力.
学习活动设计
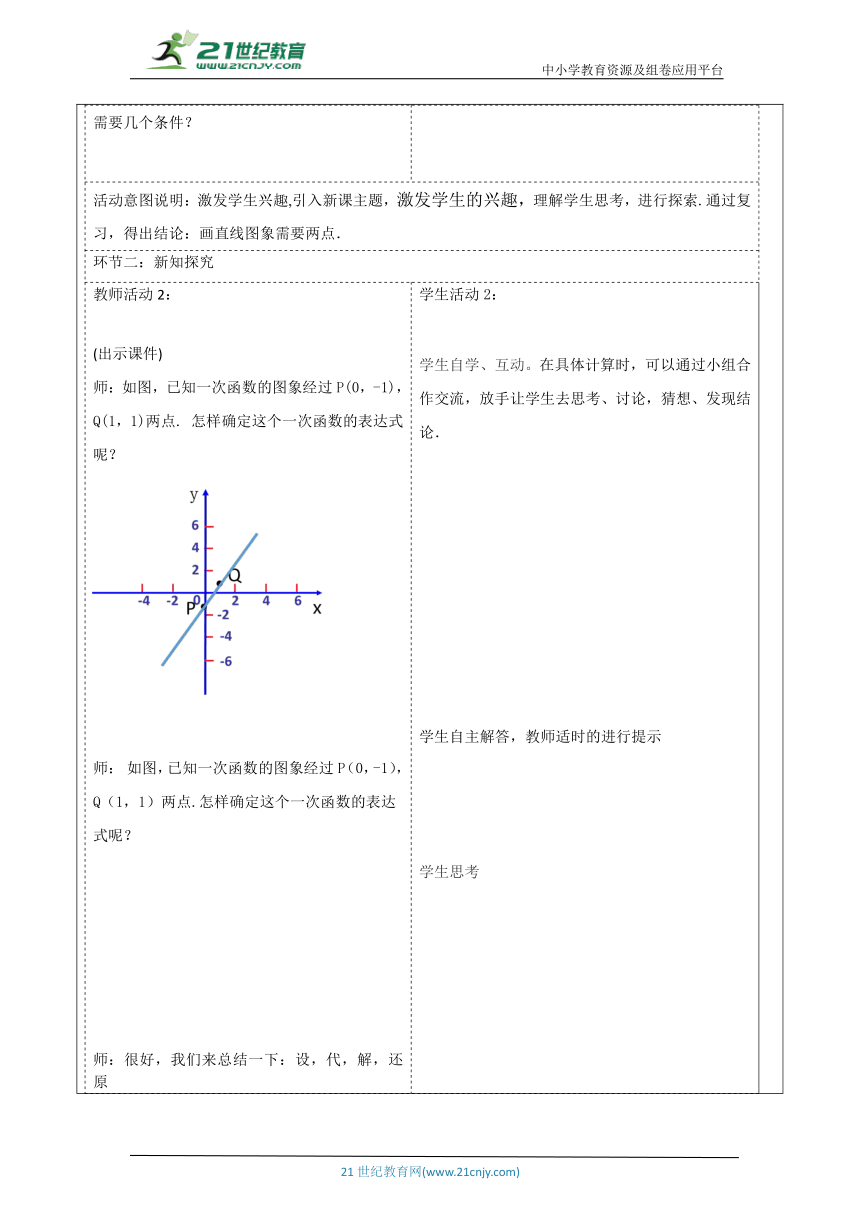
教师活动学生活动环节一:引入新课师:我们在画函数y=3x-1时,应选取几个点?为什么? 生:当x=0时,y=-1;当y=0时,x= 所以,此直线过(0,-1)、(,0)两点 师:反过来已知一个一次函数的图象经过具体的点,你能求出它的解析式吗? 师:再回忆,确定正比例函数的解析式y=kx,需求哪个值?需要几个条件? 确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件? 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:激发学生兴趣,引入新课主题,激发学生的兴趣,理解学生思考,进行探索.通过复习,得出结论:画直线图象需要两点. 环节二:新知探究教师活动2: (出示课件) 师:如图,已知一次函数的图象经过P(0,-1),Q(1,1)两点. 怎样确定这个一次函数的表达式呢? 师: 如图,已知一次函数的图象经过P(0,-1),Q(1,1)两点.怎样确定这个一次函数的表达式呢? 师:很好,我们来总结一下:设,代,解,还原 像这样,通过先设定函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数的表达式的方法称为待定系数法。 师:学生回答的很好 师:你能归纳出待定系数法求函数解析式的基本步骤吗? 师:函数解析式和函数图象如何相互转化呢? 课件展示: 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,让学生在小组内共同合作.归纳出待定系数法求函数解析式的基本步骤要求出一次函数的表达式,关键是要确定k,b的值(即待定的系数。)环节三:典例精析 例1、温度的度量有两种:摄氏温度和华氏温度。在1个标准大气压下,水的沸点是100 ℃,用华氏温度度量为212 °F;水的冰点是0 ℃,用华氏温度度量为32 °F。已知摄氏温度与华氏温度满足一次函数关系,你能不能想出一个办法将华氏温度换算成摄氏温度? 师:我们来小试一下身手吧 课件展示练习: 已知一次函数的图象如下图,写出它的关系式. 师:我们再来看这个例题 例2 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示。 (1)求y关于x的函数表达式; (2)一箱油可供拖拉机工作几小时? 师:同学们是不是掌握了呢?练一练吧 课件展示练习 已知弹簧的长度y(cm)在一定的限度内是所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式. 学生活动3: 参与教师分析和讲例题. 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,学生能在不同的条件下运用待定系数法求出一次函数的解析式.
板书设计
课堂练习 【知识技能类作业】 必做题: 1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( ) A(-1,1) B(2,2) C(-2,2) D (2,一2) 选做题: 2.一次函数y=3x+b的图象过坐标原点,则b的值为____. 【综合拓展类作业】 3.已知一次函数的图象如下图,写出它的关系式.
课堂总结
作业设计 【知识技能类作业】 必做题: 1.如图,直线AB对应的函数表达式是( ) A.y=-x+3 B.y=x+3 C.y=-x+3 D.y=x+3 选做题: 2.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是_______. 【综合拓展类作业】 3.一次函数y=kx+4的图象经过点(-3,-2),则 (1)求这个函数表达式; (2)建立适当坐标系,画出该函数的图象; (3)判断(-5,3)是否在此函数的图象上 (4)把这条直线向下平移4个单位长度后的函数关系式是__________
教学反思
21世纪教育网(www.21cnjy.com)
分课时教学设计
第6课时《4.4用待定系数法确定一次函数表示式 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 充分让学生合作探究,培养学生自主学习的能力,增进学生之间的友谊.
学习者分析 数形结合思想和归纳总结能力.
教学目标 待定系数法求一次函数的解析式。体会二元一次方程组的应用.
教学重点 让学生能在不同的条件下运用待定系数法求出一次函数的解析式 .
教学难点 用待定系数法求一次函数的解析式,渗透数形结合思想和归纳总结能力.
学习活动设计
教师活动学生活动环节一:引入新课师:我们在画函数y=3x-1时,应选取几个点?为什么? 生:当x=0时,y=-1;当y=0时,x= 所以,此直线过(0,-1)、(,0)两点 师:反过来已知一个一次函数的图象经过具体的点,你能求出它的解析式吗? 师:再回忆,确定正比例函数的解析式y=kx,需求哪个值?需要几个条件? 确定一次函数的解析式y=kx+b,需求哪个值?需要几个条件? 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:激发学生兴趣,引入新课主题,激发学生的兴趣,理解学生思考,进行探索.通过复习,得出结论:画直线图象需要两点. 环节二:新知探究教师活动2: (出示课件) 师:如图,已知一次函数的图象经过P(0,-1),Q(1,1)两点. 怎样确定这个一次函数的表达式呢? 师: 如图,已知一次函数的图象经过P(0,-1),Q(1,1)两点.怎样确定这个一次函数的表达式呢? 师:很好,我们来总结一下:设,代,解,还原 像这样,通过先设定函数表达式(确定函数模型),再根据条件确定表达式中的未知系数,从而求出函数的表达式的方法称为待定系数法。 师:学生回答的很好 师:你能归纳出待定系数法求函数解析式的基本步骤吗? 师:函数解析式和函数图象如何相互转化呢? 课件展示: 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:从旧知识出发,呼应引课问题,学生通过自己解决问题,让学生在小组内共同合作.归纳出待定系数法求函数解析式的基本步骤要求出一次函数的表达式,关键是要确定k,b的值(即待定的系数。)环节三:典例精析 例1、温度的度量有两种:摄氏温度和华氏温度。在1个标准大气压下,水的沸点是100 ℃,用华氏温度度量为212 °F;水的冰点是0 ℃,用华氏温度度量为32 °F。已知摄氏温度与华氏温度满足一次函数关系,你能不能想出一个办法将华氏温度换算成摄氏温度? 师:我们来小试一下身手吧 课件展示练习: 已知一次函数的图象如下图,写出它的关系式. 师:我们再来看这个例题 例2 某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示。 (1)求y关于x的函数表达式; (2)一箱油可供拖拉机工作几小时? 师:同学们是不是掌握了呢?练一练吧 课件展示练习 已知弹簧的长度y(cm)在一定的限度内是所挂重物质量x(千克)的一次函数,现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米.求这个一次函数的关系式. 学生活动3: 参与教师分析和讲例题. 活动意图说明:熟练掌握.巩固学的知识,学生通过自己解决问题,充分发挥学习的主动性,学生能在不同的条件下运用待定系数法求出一次函数的解析式.
板书设计
课堂练习 【知识技能类作业】 必做题: 1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过点( ) A(-1,1) B(2,2) C(-2,2) D (2,一2) 选做题: 2.一次函数y=3x+b的图象过坐标原点,则b的值为____. 【综合拓展类作业】 3.已知一次函数的图象如下图,写出它的关系式.
课堂总结
作业设计 【知识技能类作业】 必做题: 1.如图,直线AB对应的函数表达式是( ) A.y=-x+3 B.y=x+3 C.y=-x+3 D.y=x+3 选做题: 2.一次函数y=kx+b,当3≤x≤4时,3≤y≤6,则的值是_______. 【综合拓展类作业】 3.一次函数y=kx+4的图象经过点(-3,-2),则 (1)求这个函数表达式; (2)建立适当坐标系,画出该函数的图象; (3)判断(-5,3)是否在此函数的图象上 (4)把这条直线向下平移4个单位长度后的函数关系式是__________
教学反思
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
