数学:1.1.2《平面变换》教案(人教版选修4-2)
文档属性
| 名称 | 数学:1.1.2《平面变换》教案(人教版选修4-2) |
|
|
| 格式 | rar | ||
| 文件大小 | 249.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-31 20:12:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.1.2平面变换——恒等变换
1.恒等变换
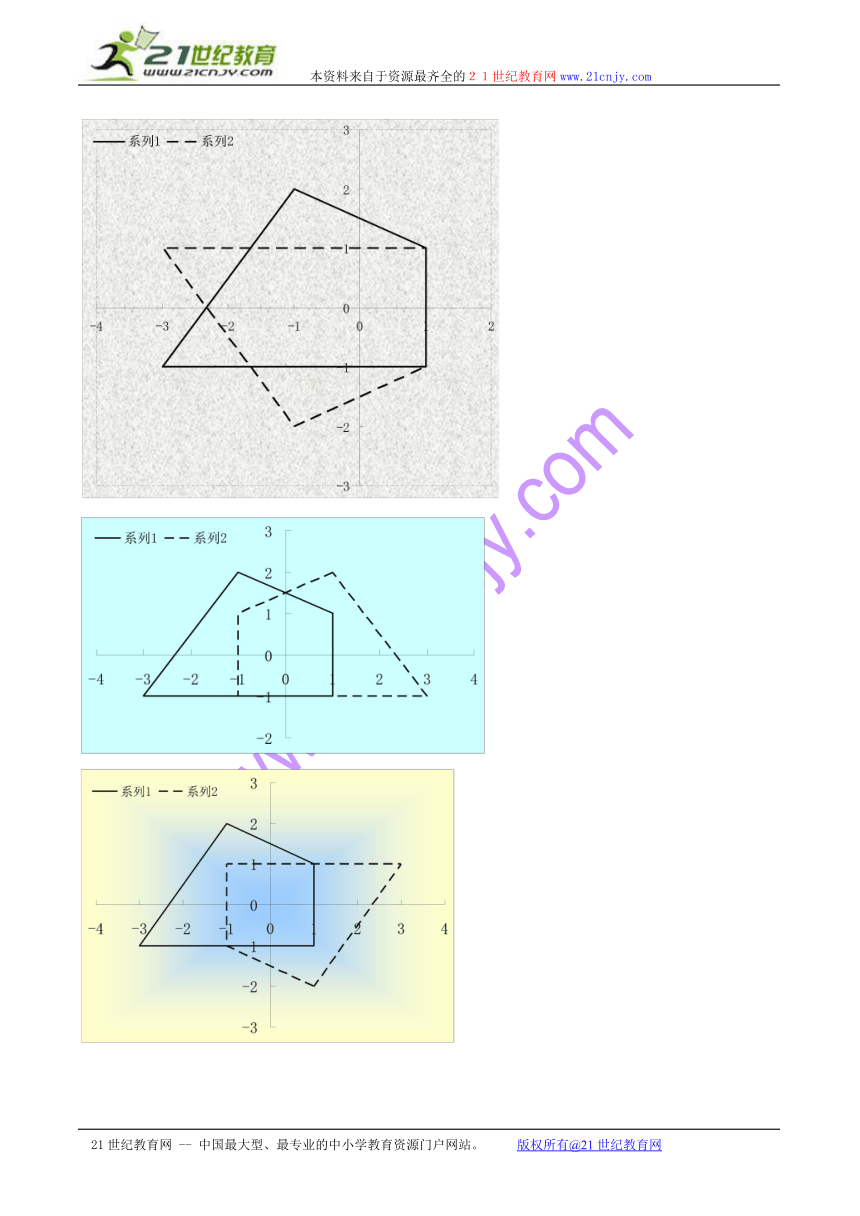
将图中所示的四边形ABCD保持位置不变,能否用矩阵M来表示?
2.伸压变换——能否用矩阵来表示下列图形的变换?
例1已知曲线y=sinx经过变换T作用后变为新的曲线y=sin2x,画出相关的图象,并求出变换T对应的矩阵M。
例2 验证圆C:x2+y2=1在矩阵A=对应的伸压变换下变为一椭圆,并求出此椭圆的方程。
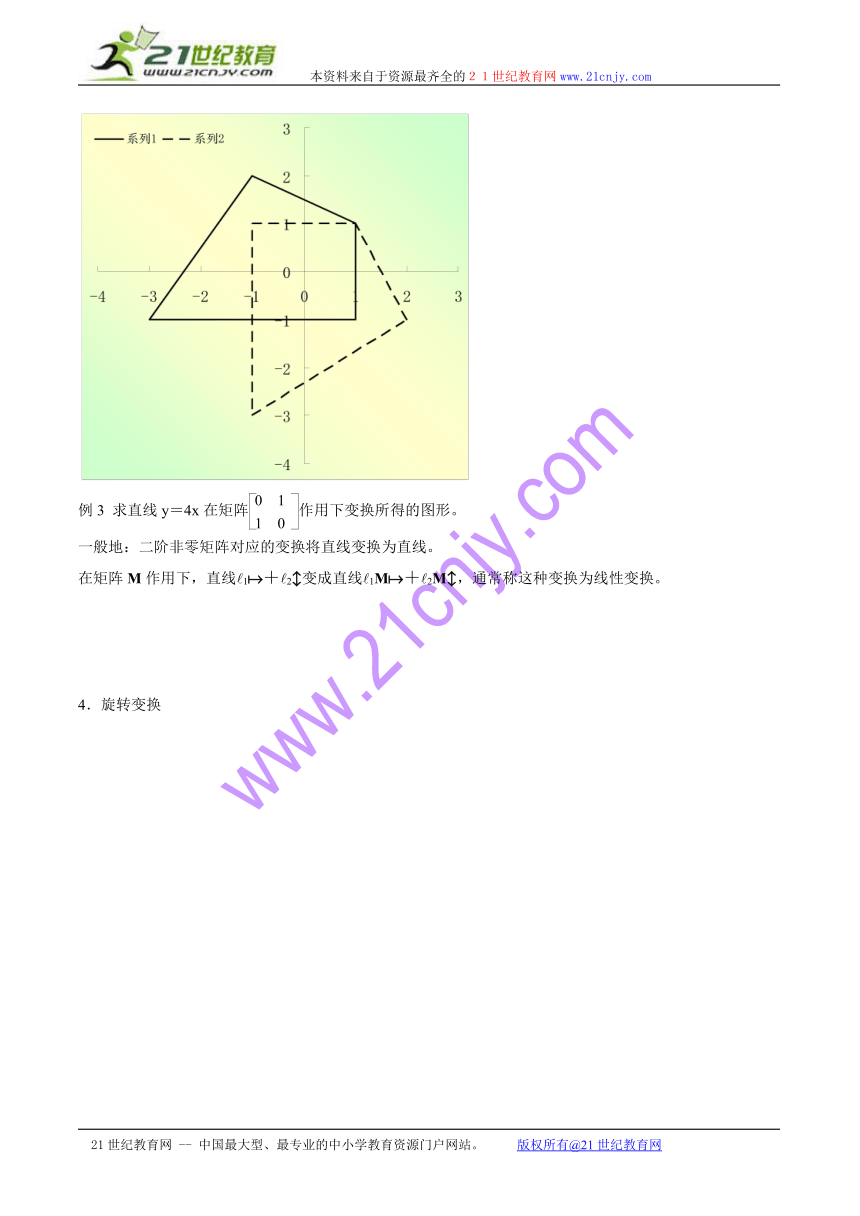
3.反射变换
例3 求直线y=4x在矩阵作用下变换所得的图形。
一般地:二阶非零矩阵对应的变换将直线变换为直线。
在矩阵M作用下,直线1+2变成直线1M+2M,通常称这种变换为线性变换。
4.旋转变换
例4 已知A(0,0),B(2,0),C(2,1),D(0,1),求矩形ABCD绕原点逆时针旋转90 后得到的图形,并求出其顶点的坐标。
5.投影变换
6.切变变换
例5 已知矩形ABCD在变换T的作用下变成图形ABCD,试求变换对应的矩阵M。
例6 已知矩形ABCD在变换T的作用下变成图形ABCD,试求变换对应的矩阵M。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.1.2平面变换——恒等变换
1.恒等变换
将图中所示的四边形ABCD保持位置不变,能否用矩阵M来表示?
2.伸压变换——能否用矩阵来表示下列图形的变换?
例1已知曲线y=sinx经过变换T作用后变为新的曲线y=sin2x,画出相关的图象,并求出变换T对应的矩阵M。
例2 验证圆C:x2+y2=1在矩阵A=对应的伸压变换下变为一椭圆,并求出此椭圆的方程。
3.反射变换
例3 求直线y=4x在矩阵作用下变换所得的图形。
一般地:二阶非零矩阵对应的变换将直线变换为直线。
在矩阵M作用下,直线1+2变成直线1M+2M,通常称这种变换为线性变换。
4.旋转变换
例4 已知A(0,0),B(2,0),C(2,1),D(0,1),求矩形ABCD绕原点逆时针旋转90 后得到的图形,并求出其顶点的坐标。
5.投影变换
6.切变变换
例5 已知矩形ABCD在变换T的作用下变成图形ABCD,试求变换对应的矩阵M。
例6 已知矩形ABCD在变换T的作用下变成图形ABCD,试求变换对应的矩阵M。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
