广东市深圳市2025年小升初模拟测试卷(含解析)
文档属性
| 名称 | 广东市深圳市2025年小升初模拟测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 801.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 05:51:31 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
广东市深圳市2025年小升初模拟测试卷
一、填空题
1.在括号里填上合适的数或单位。
2023年2月15日,小伍家的蓄水池开工建设,到2023年3月12日完工,从开工到完工一共 天。注满蓄水池共需16 的水。(填体积单位)
2.0.6平方千米= 公顷 2千克20克= 千克
3.∶0.75化成最简单的整数比是 ,比值是 。
4.根据3a=5b(a、b不为0),写出一个比例是 ∶ = ∶ 。
5.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
6.一个最简真分数,分子、分母的积是24,这个真分数是 或 。
7.把一个半径是5cm的圆等分成若干份后拼成一个近似长方形,长方形的周长比原来圆的周长增加 cm,长方形的面积是 cm2。
8.观察如图线段图,按要求填空。
(1)小伍根据等量关系 可以列出算式“80-80×。
(2)小娅列出算式为“80×(1-)”,其中“1-”表示的意义: 。
9.某男装专卖店所有服装都打同样的折扣销售。王叔叔买了一件上衣,原价250元,现价200元。他还想买一条裤子,原价180元,现价 元。
10.下面图形是由若下个圆按规律组成的,第6个图形中有 个圆,第n个图形中有 个圆。
二、选择题
11.一个小数,由6个十与4个百分之一组成,这个小数是( )。
A.6.04 B.6.4 C.60.4 D.60.04
12.如果规定向东走3m记作﹢3m,那么向西走2m可以记作( )。
A.﹣3m B.﹢2m C.﹣2m D.﹢3m
13.亮亮调查了华南植物园各种植物的数量情况,如果要用统计图表示各种植物占植物总数的百分比,应选择( )。
A.折线统计图 B.条形统计图
C.扇形统计图 D.以上三种都可以
14.一台电视机原价4800元,现在打八五折出售,便宜了多少元?正确的列式是( )。
A.4800÷85% B.4800×85%
C.4800×(1-85%) D.4800÷(1-85%)
15.一个公司有50名员工,今天有2人请假未到。这个公司今天的出勤率是( )。
A.2% B.96% C.48% D.4%
16.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是( )。
A. B.
C. D.
17.小明每天步行锻炼身体,他小时走了千米。小明步行的速度是( )。
A.5千米 B.千米/小时 C.5千米/小时 D.千米/小时
18.已知,那么、、的关系是( )。
A. B. C. D.
19.一个三角形,三个角的度数比是1∶2∶3,按角分( )。
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
20.赵伟家的客厅长6米,宽4.8米。计划在地面上铺方砖,要求都用整块的方砖,且正好铺满,需要( )。
A.50厘米 B.60厘米 C.80厘米 D.100厘米
三、计算题
21.直接写得数。
8÷2.2= 1-= 1.5×6= +=
3.5÷= ×= +2= ×20%=
22.用你喜欢的方法计算。
6.53-(3.53+) 25×32×125
36÷[(-)×3] 2.25×4.8+77.5×0.48
23.求未知数x。
20%x+1.5=18.5 x-x=3.2 42∶=x∶
四、作图题
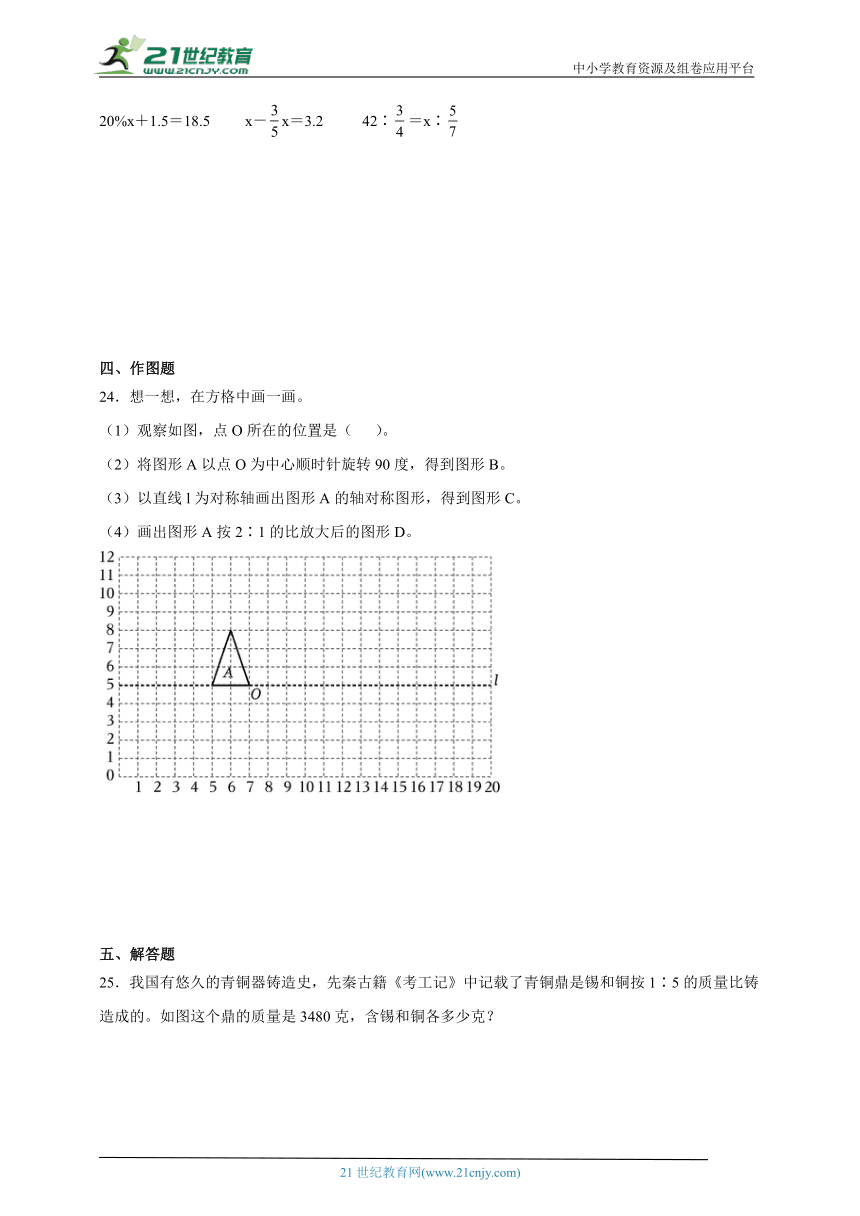
24.想一想,在方格中画一画。
(1)观察如图,点O所在的位置是( )。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C。
(4)画出图形A按2∶1的比放大后的图形D。
五、解答题
25.我国有悠久的青铜器铸造史,先秦古籍《考工记》中记载了青铜鼎是锡和铜按1∶5的质量比铸造成的。如图这个鼎的质量是3480克,含锡和铜各多少克?
26.“日啖荔枝三百颗,不辞长作岭南人”。现在正值荔枝成熟季节,张大伯的商铺今年通过“直播带货”打开了销路,平均每天线上销售量约为930千克,相比之前线下的销售量增长了520%,线下平均每天销售量是多少千克?(列方程解答)
27.如图,一个底面直径是20厘米的圆柱形容器,将一个底面半径是3厘米,高是10厘米的圆锥形铁块完全浸入水中。当把铁块取出时,这时水面的高度会下降多少厘米?
28.一分钟踢毽子决赛,前3名选手的前三轮成绩如表所示。
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36
笑笑 45 48 30
妙想 40 41 45
(1)按平均分排名,谁获得第一名?
(2)按单轮成绩最高排名,谁获得第一名?
(3)实际结果笑笑是本次冠军,你猜本次比赛按什么规则排名?并分析这个规则的优缺点。
29.某游泳馆推出两种付费方式:方式一,单次卡,每次收费30元;方式二,办理会员年卡,一次缴纳240元会员费,每次游泳另外收费14元(一年内有效)。
(1)李叔叔游泳锻炼的计划是一年,每月两次。他选择哪种方式更划算?
(2)一年内游泳达到几次时,两种付费方式所用钱数相等?
30.正六边形的边长为4厘米,六个圆形的圆心分别在六边形的顶点上。如果小圆的半径为1厘米,求浅灰色部分与深灰色部分面积之比。
《广东市深圳市2025年小升初模拟测试卷》参考答案
题号 11 12 13 14 15 16 17 18 19 20
答案 D C C C B C C B B B
1. 26 立方米/m3
【分析】先根据平年和闰年的判断方法,用2023除以4,不能整除,则2023年是平年,2月份有28天。已知2023年2月15日开工到2023年3月12日完工,那么2月份开工的天数是(28-15+1)天,再加上3月份开工的12天,即可求出从开工到完工一共的天数。
棱长1米的正方体,体积是1立方米,一台小冰柜的体积大约是1立方米,所以计量注满蓄水池需水的体积用“立方米”作单位比较合适。
【详解】2023÷4=505……3
2023年是平年,2月有28天。
2月份开工: 28-15+1=14(天)
开工到完工一共:14+12=26(天)
2023年2月15日,小伍家的蓄水池开工建设,到2023年3月12日完工,从开工到完工一共26天。注满蓄水池共需16立方米的水。
2. 60 2.02
【分析】根据1平方千米=100公顷,1千克=1000克,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【详解】(公顷)
(千克)
0.6平方千米=60公顷 2千克20克=2.02千克
3. 2∶1 2
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。利用“比的基本性质”把比化简成最简单的整数比。
用比的前项除以比的后项所得的商,叫做比值。根据比值的意义,用最简比的前项除以比的后项即得比值。
【详解】∶0.75
=∶
=(×4)∶(×4)
=6∶3
=(6÷3)∶(3÷3)
=2∶1
2∶1
=2÷1
=2
∶0.75化成最简单的整数比是2∶1,比值是2。
4. a b 5 3
【分析】比例的性质:比例的两内项之积等于两外项之积。据此,可将3和a看作两内项,写出比例;也可将3和a看作两外项,写出比例。据此填空。(本题答案不唯一)
【详解】把3和a看作两外项,写出的比例可以是a∶b=5∶3。(答案不唯一)
5. ② ③
【分析】观察图形,再添加一个同样的小方块,从左面看到的图形不变,说明从左面看不到某位置上新放的小方块,据此得出添加的小方块放在②号位置上;
再添加一个同样的小方块,从前面看到的图形不变,说明从前面看不到某位置上新放的小方块,据此得出添加的小方块应放在③号位置上。
【详解】如图:
在②号位置上面放一个同样的小方块,从左面看:
在③号位置上面放一个同样的小方块,从前面看:
填空如下:
在 ② 号位置上面放一个同样的小方块,从左面看到的图形不变,在 ③ 号位置上面放一个同样的小方块,从前面看到的图形不变。
6.
【分析】分子比分母小的分数叫作真分数;分子比分母大或分子和分母相等的分数叫作假分数;分子和分母只有公因数1,像这样的分数叫作最简分数;先按顺序列举出两个整数积为24的算式,再找出能组成最简真分数的两个数,即可求得。
【详解】1×24=24
2×12=24
3×8=24
4×6=24
分子、分母的积是24的最简真分数有和。
7. 10 78.5
【分析】把一个圆等分成若干份后拼成一个近似长方形,这个长方形的长是圆周长的一半,宽是圆的半径。
(1)求长方形的周长比圆的周长增加的部分:拼成后的长方形的周长比圆的周长多了圆的两个半径,据此计算即可。
(2)求长方形的面积:因为长方形的面积等于圆的面积,根据圆的面积公式S=πr2,即可求解。
【详解】(cm)
(cm2)
长方形的周长比原来圆的周长增加10cm,长方形的面积是78.5cm2。
8.(1)已行路程=总路程-剩下路程
(2)已行路程占总路程的几分之几
【分析】(1)从线段图可知,总路程是80千米,剩下总路程的。根据求一个数的几分之几是多少,用乘法解答,那么剩下的路程就是总路程80千米乘剩下路程占总路程的,即80×千米。根程80千米减去剩下的路程80×千米,据这个运算逻辑,其依据的等量关系就是:总路程一剩下的路程=已行的路程。
(2)把总路程看作单位“1”,已知剩下路程占总路程的,用1-这样得到的就是已行路程占总路程的几分之几。
乐乐列出的算式“80 ×(1-)”,就是用总路程80千米乘已行路程占总路程的分率(1-),从而求出已行的路程。
【详解】(1)由分析可知:小伍根据等量关系:已行路程=总路程-剩下路程可以列出算式“80-80×”。
(2)由分析可知:小娅列出算式为“80×(1-)”,其中“1-”表示的意义:已行路程占总路程的几分之几。
9.144
【分析】已知一件上衣原价250元,现价200元,用现价除以原价,求出现价是原价的百分之几;
已知买一条原价180元的裤子,把原价看作单位“1”,根据求一个数的百分之几是多少,用乘法计算,求出这条裤子的现价。
【详解】200÷250×100%
=0.8×100%
=80%
180×80%
=180×0.8
=144(元)
现价144元。
10. 37 (n2+1)
【分析】先观察前几个图形中圆的数量,尝试找出数量与图形序号之间的联系,进而得出第6个图形中圆的数量以及第n个图形中圆的数量的表达式。
【详解】第1个图形:有1+1=2个圆,这里前面的1可以看作是,即+1=2。
第2个图形:有4+1=5个圆,其中4恰好是,也就是+1=5。
第3个图形:有9+1=10个圆,9是,即+1=10。
第4个图形:有16+1=17个圆,16是,即+1=17。
……
第6个图形圆的个数有:+1=37(个)
发现规律:第n个图形中圆的数量是(+1)个。
填空如下:
所以第6个图形中有(37)个圆,第n个图形中有(+1)个圆。
11.D
【分析】已知一个小数,由6个十,即十位上是6;4个百分之一,即百分位上是4;其它数位上用0占位,据此写出这个小数。
【详解】一个小数,由6个十与4个百分之一组成,这个小数是60.04。
故答案为:D
12.C
【分析】正数、负数表示两种相反意义的量。如果规定向东走记作正,那么向西走就记作负。
【详解】如果规定向东走3m记作﹢3m,那么向西走2m可以记作﹣2m。
故答案为:C
13.C
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】亮亮调查了华南植物园各种植物的数量情况,如果要用统计图表示各种植物占植物总数的百分比,应选择(扇形统计图)。
故答案为:C
14.C
【分析】一台电视机打八五折出售,那么就是指现价比原价便宜(1-85%),求便宜多少元,利用原价乘便宜的折扣即可。
【详解】4800×(1-85%)
=4800×15%
=720(元)
所以便宜了720元。
因此正确的列式是4800×(1-85%)。
故答案为:C
15.B
【分析】根据题意,先用员工总人数减去今天请假的人数,求出今天出勤的人数;再根据“出勤率=出勤人数÷总人数×100%”,求出今天的出勤率。
【详解】(50-2)÷50×100%
=48÷50×100%
=0.96×100%
=96%
这个公司今天的出勤率是96%。
故答案为:B
16.C
【分析】根据题意,每月用水量6吨以内每吨2.5元,则每月6吨以内的水费是从0开始的一条线段;超过6吨的部分每吨3元,3大于2.5,超过6吨部分水费上升速度比6吨以内的要大,所以超过6吨部分的线段比6吨以内的线段要陡一些,据此找出能正确表示每月水费与用水量关系的折线统计图。
【详解】A.是一条从0开始的线段,表示水费的单价固定不变,不符合题意;
B.超过6吨部分的水费保持不变,不随用水量的增加而增加,不符合题意;
C.用水量超过6吨的线段比6吨以内的线段要陡,表示超过6吨的单价比6吨以内的单价要贵,符合题意;
D.折线的拐点在3吨,表示用水量超过3吨,单价上涨,不符合题意。
故答案为:C
17.C
【分析】根据“速度=路程÷时间”代入数据计算即可。
【详解】÷=×3=5(千米/小时)
所以小明步行的速度是5千米/小时。
故答案为:C
18.B
【分析】观察三个加法算式的得数相等,可以设它们的得数是1;根据“加数=和-一个加数”,求出、、的值,再比较大小即可。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小。
【详解】设;
那么、、的关系是。
故答案为:B
19.B
【分析】三角形的内角和是180°,因三个内角的度数比是1∶2∶3,最大角就占了三角形内角和的,根据分数乘法的意义,算出最大角,即可判断是什么三角形。
【详解】180×
=180×
=90°
一个角是直角的三角形是直角三角形。
故答案为:B
20.B
【分析】先根据进率“1米=100厘米”把6米换算成600厘米,4.8米换算成480厘米;
在长600厘米、宽480厘米的地面上铺方砖,要求都用整块的方砖,且正好铺满,那么方砖的边长是600和480的公因数;
先把600和480分解质因数,把公有的相同质因数乘起来即是它们的最大公因数,再列举这个最大公因数的所有因数,即是600和480的公因数,从各选项中找出哪个数是600和480的公因数,即是方砖的边长。
【详解】6米=600厘米
4.8米=480厘米
600=2×2×2×3×5×5
480=2×2×2×2×2×3×5
600和480的最大公因数是:2×2×2×3×5=120
120的因数:1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120;
A.50不是600和480的公因数,所以边长为50厘米的方砖不能正好铺满;
B.60是600和480的公因数,所以边长为60厘米的方砖能正好铺满;
C.80不是600和480的公因数,所以边长为80厘米的方砖不能正好铺满;
D.100不是600和480的公因数,所以边长为100厘米的方砖不能正好铺满。
故答案为:B
21.;;9;;
7;;4;0.05
【解析】略
22.2.5;100000;
24;48
【分析】(1)根据减法的性质:一个数减去两个数的和,等于这个数依次减去这两个数。据此计算;
(2)根据乘法结合律进行计算;
(3)先算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法;
(4)先根据积不变的规律把转化为,再根据乘法分配律进行计算。
【详解】(1)6.53-(3.53+)
=6.53-3.53-
=3-
=3-0.5
=2.5
(2)25×32×125
=25×(4×8)×125
=(25×4)×(8×125)
=100×1000
=100000
(3)36÷[(-)×3]
=36÷[(-)×3]
=36÷[×3]
=36÷
=36×
=24
(4)2.25×4.8+77.5×0.48
=2.25×4.8+7.75×4.8
=(2.25+7.75)×4.8
=10×4.8
=48
23.x=85;x=8;x=40
【分析】首先根据等式的性质,两边同时减去1.5,然后两边再同时除以0.2(20%=0.2)即可;
首先把x-x=3.2化成0.4x=3.2,然后根据等式的性质,两边同时除以0.4即可;
首先根据比例的基本性质化简,可得x=42×,然后根据等式的性质,两边同时乘即可。
【详解】20%x+1.5=18.5
解:0.2x+1.5=18.5
0.2x+1.5-1.5=18.5-1.5
0.2x=17
0.2x÷0.2=17÷0.2
x=85
(2)x-x=3.2
解:x-0.6x=3.2
0.4x=3.2
0.4x÷0.4=3.2÷0.4
x=8
(3)42∶=x∶
解:x=42×
x=30
x×=30×
x=40
24.(1)(7,5)
(2)(3)(4)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O所在的位置。
(2)根据旋转的特征,将图形A以点O为中心顺时针旋转90度,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形B。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴l的对称点后,依次连接各点得到图形A的对称图形C。
(4)图形A按2∶1的比放大,即把图形A的每条边都扩大到原来的2倍,据此画出放大后的图形D。
【详解】(1)观察如图,点O所在的位置是(7,5)。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B,如下图。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C,如下图。
(4)放大后三角形的底:2×2=4
放大后三角形的高:3×2=6
则画一个底为4、高为6的三角形D,如下图。
25.锡580克;铜2900克
【分析】将比的前后项看成份数,鼎的质量÷总份数=一份数,一份数分别乘锡和铜的对应份数,即可求出锡和铜的质量。
【详解】3480÷(1+5)
=3480÷6
=580(克)
580×1=580(克)
580×5=2900(克)
答:含锡580克,铜2900克。
26.150千克
【分析】设线下平均每天销售量是x千克;把线下平均每天销售量看作单位“1”,线上平均每天销售量是线下的(1+520%),用线下平均每天销售量×(1+520%)=线上平均每天销售量,据此列方程:x×(1+520%)=930,解方程,即可解答。
【详解】解:设线下平均每天销售量是x千克。
x×(1+520%)=930
6.2x=930
x=930÷6.2
x=150
答:线下平均每天销售量是150千克。
27.0.3厘米
【分析】根据体积的意义可知,当把圆锥形铁块从容器中取出后,下降部分水的体积就等于这个圆锥形铁块的体积。
先根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积;
根据圆的面积公式,求出圆柱的底面积;再根据圆柱的高,用下降部分水的体积除以除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】×3.14×32×10÷[3.14×(20÷2)2]
=×3.14×9×10÷[3.14×102]
=×3.14×9×10÷[3.14×100]
=94.2÷314
=0.3(厘米)
答:这时水面的高度会下降0.3厘米。
28.(1)妙想
(2)淘气
(3)按第一轮的成绩进行排名的。优点:规则简便容易操作;缺点:不能准确反映三人的真实水平。(说法不唯一)
【分析】(1)先根据“平均数=数据和÷数据个数”,求出三人的平均成绩,再比较大小即可;
(2)分别比较出三轮成绩中9个数字的大小,看谁的单轮成绩最高即可;
(3)先确定是根据平均数还是单轮成绩确定了笑笑是本次冠军,然后分析这个规则的优缺点即可。
【详解】(1)(25+50+36)÷3
=111÷3
=37(个)
(45+48+30)÷3
=123÷3
=41(个)
(40+41+45)÷3
=126÷3
=42(个)
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36 37
笑笑 45 48 30 41
妙想 40 41 45 42
42个>41个>37个
答:按平均分排名,妙想获得第一名。
(2)25个<30个<36个<40个<41个<45个<48个<50个
答:按单轮成绩最高排名,淘气获得第一名。
(3)按单轮成绩最高排名,淘气获得第一名;按平均分排名,妙想获得第一名。
按第一轮成绩排名:25个<40个<45个,笑笑获得第一名;
按第二轮成绩排名:41个<48个<50个,淘气获得第一名;
按第三轮成绩排名:30个<36个<45个,妙想获得第一名;
由此可知:笑笑是本次冠军,是按第一轮的成绩进行排名的。
优点:规则简便容易操作;缺点:不能准确反映三人的真实水平。(说法不唯一)
29.(1)方式二
(2)15次
【分析】(1)分别计算出两种方式的实际钱数,比较即可。一年有12个月,方式一:单价×数量=总价,每月次数×月数=总次数,单价×总次数=实际钱数;方式二:每次另外收费钱数×总次数,然后再加上240元的会员费是实际钱数。
(2)两种方式,游泳次数相同,每次相差16元,240元里面有几个16元,就有几次。
【详解】(1)方式一:30×(12×2)
=30×24
=720(元)
方式二:240+14×(12×2)
=240+14×24
=240+336
=576(元)
720>576
答:他选择方式二更划算。
(2)240÷(30-14)
=240÷16
=15(次)
答:一年内游泳达到15次时,两种付费方式所用钱数相等。
30.1∶2
【分析】正六边形的内角和是720度,相当于两个圆的内角和,所以浅灰色部分的面积=一个小圆的面积+一个大圆的面积;那么外面深灰色部分面积=2个小圆的面积+2个大圆的面积;即外面深灰色部分面积=2×(一个小圆的面积+一个大圆的面积);所以面积比是1∶2;据此解答即可。
【详解】根据分析可得:
浅灰色部分的面积=一个小圆的面积+一个大圆的面积
深灰色部分面积=2个小圆的面积+2个大圆的面积=2×(一个小圆的面积+一个大圆的面积)=2×浅灰色部分的面积;
所以浅灰色部分与深灰色部分面积之比是1∶2。
【点睛】在求不规则图形面积时,往往利用割补结合:观察图形,把图形分割,再进行移补,形成一个容易求得的图形进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
广东市深圳市2025年小升初模拟测试卷
一、填空题
1.在括号里填上合适的数或单位。
2023年2月15日,小伍家的蓄水池开工建设,到2023年3月12日完工,从开工到完工一共 天。注满蓄水池共需16 的水。(填体积单位)
2.0.6平方千米= 公顷 2千克20克= 千克
3.∶0.75化成最简单的整数比是 ,比值是 。
4.根据3a=5b(a、b不为0),写出一个比例是 ∶ = ∶ 。
5.如图所示,在 号位置上面放一个同样的小方块,从左面看到的图形不变,在 号位置上面放一个同样的小方块,从前面看到的图形不变。
6.一个最简真分数,分子、分母的积是24,这个真分数是 或 。
7.把一个半径是5cm的圆等分成若干份后拼成一个近似长方形,长方形的周长比原来圆的周长增加 cm,长方形的面积是 cm2。
8.观察如图线段图,按要求填空。
(1)小伍根据等量关系 可以列出算式“80-80×。
(2)小娅列出算式为“80×(1-)”,其中“1-”表示的意义: 。
9.某男装专卖店所有服装都打同样的折扣销售。王叔叔买了一件上衣,原价250元,现价200元。他还想买一条裤子,原价180元,现价 元。
10.下面图形是由若下个圆按规律组成的,第6个图形中有 个圆,第n个图形中有 个圆。
二、选择题
11.一个小数,由6个十与4个百分之一组成,这个小数是( )。
A.6.04 B.6.4 C.60.4 D.60.04
12.如果规定向东走3m记作﹢3m,那么向西走2m可以记作( )。
A.﹣3m B.﹢2m C.﹣2m D.﹢3m
13.亮亮调查了华南植物园各种植物的数量情况,如果要用统计图表示各种植物占植物总数的百分比,应选择( )。
A.折线统计图 B.条形统计图
C.扇形统计图 D.以上三种都可以
14.一台电视机原价4800元,现在打八五折出售,便宜了多少元?正确的列式是( )。
A.4800÷85% B.4800×85%
C.4800×(1-85%) D.4800÷(1-85%)
15.一个公司有50名员工,今天有2人请假未到。这个公司今天的出勤率是( )。
A.2% B.96% C.48% D.4%
16.某市规定每户每月用水量不超过6吨时,每吨价格为2.5元;当用水量超过6吨时,超过部分每吨价格为3元。下图中能正确表示每月水费与用水量关系的是( )。
A. B.
C. D.
17.小明每天步行锻炼身体,他小时走了千米。小明步行的速度是( )。
A.5千米 B.千米/小时 C.5千米/小时 D.千米/小时
18.已知,那么、、的关系是( )。
A. B. C. D.
19.一个三角形,三个角的度数比是1∶2∶3,按角分( )。
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
20.赵伟家的客厅长6米,宽4.8米。计划在地面上铺方砖,要求都用整块的方砖,且正好铺满,需要( )。
A.50厘米 B.60厘米 C.80厘米 D.100厘米
三、计算题
21.直接写得数。
8÷2.2= 1-= 1.5×6= +=
3.5÷= ×= +2= ×20%=
22.用你喜欢的方法计算。
6.53-(3.53+) 25×32×125
36÷[(-)×3] 2.25×4.8+77.5×0.48
23.求未知数x。
20%x+1.5=18.5 x-x=3.2 42∶=x∶
四、作图题
24.想一想,在方格中画一画。
(1)观察如图,点O所在的位置是( )。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C。
(4)画出图形A按2∶1的比放大后的图形D。
五、解答题
25.我国有悠久的青铜器铸造史,先秦古籍《考工记》中记载了青铜鼎是锡和铜按1∶5的质量比铸造成的。如图这个鼎的质量是3480克,含锡和铜各多少克?
26.“日啖荔枝三百颗,不辞长作岭南人”。现在正值荔枝成熟季节,张大伯的商铺今年通过“直播带货”打开了销路,平均每天线上销售量约为930千克,相比之前线下的销售量增长了520%,线下平均每天销售量是多少千克?(列方程解答)
27.如图,一个底面直径是20厘米的圆柱形容器,将一个底面半径是3厘米,高是10厘米的圆锥形铁块完全浸入水中。当把铁块取出时,这时水面的高度会下降多少厘米?
28.一分钟踢毽子决赛,前3名选手的前三轮成绩如表所示。
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36
笑笑 45 48 30
妙想 40 41 45
(1)按平均分排名,谁获得第一名?
(2)按单轮成绩最高排名,谁获得第一名?
(3)实际结果笑笑是本次冠军,你猜本次比赛按什么规则排名?并分析这个规则的优缺点。
29.某游泳馆推出两种付费方式:方式一,单次卡,每次收费30元;方式二,办理会员年卡,一次缴纳240元会员费,每次游泳另外收费14元(一年内有效)。
(1)李叔叔游泳锻炼的计划是一年,每月两次。他选择哪种方式更划算?
(2)一年内游泳达到几次时,两种付费方式所用钱数相等?
30.正六边形的边长为4厘米,六个圆形的圆心分别在六边形的顶点上。如果小圆的半径为1厘米,求浅灰色部分与深灰色部分面积之比。
《广东市深圳市2025年小升初模拟测试卷》参考答案
题号 11 12 13 14 15 16 17 18 19 20
答案 D C C C B C C B B B
1. 26 立方米/m3
【分析】先根据平年和闰年的判断方法,用2023除以4,不能整除,则2023年是平年,2月份有28天。已知2023年2月15日开工到2023年3月12日完工,那么2月份开工的天数是(28-15+1)天,再加上3月份开工的12天,即可求出从开工到完工一共的天数。
棱长1米的正方体,体积是1立方米,一台小冰柜的体积大约是1立方米,所以计量注满蓄水池需水的体积用“立方米”作单位比较合适。
【详解】2023÷4=505……3
2023年是平年,2月有28天。
2月份开工: 28-15+1=14(天)
开工到完工一共:14+12=26(天)
2023年2月15日,小伍家的蓄水池开工建设,到2023年3月12日完工,从开工到完工一共26天。注满蓄水池共需16立方米的水。
2. 60 2.02
【分析】根据1平方千米=100公顷,1千克=1000克,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【详解】(公顷)
(千克)
0.6平方千米=60公顷 2千克20克=2.02千克
3. 2∶1 2
【分析】比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。利用“比的基本性质”把比化简成最简单的整数比。
用比的前项除以比的后项所得的商,叫做比值。根据比值的意义,用最简比的前项除以比的后项即得比值。
【详解】∶0.75
=∶
=(×4)∶(×4)
=6∶3
=(6÷3)∶(3÷3)
=2∶1
2∶1
=2÷1
=2
∶0.75化成最简单的整数比是2∶1,比值是2。
4. a b 5 3
【分析】比例的性质:比例的两内项之积等于两外项之积。据此,可将3和a看作两内项,写出比例;也可将3和a看作两外项,写出比例。据此填空。(本题答案不唯一)
【详解】把3和a看作两外项,写出的比例可以是a∶b=5∶3。(答案不唯一)
5. ② ③
【分析】观察图形,再添加一个同样的小方块,从左面看到的图形不变,说明从左面看不到某位置上新放的小方块,据此得出添加的小方块放在②号位置上;
再添加一个同样的小方块,从前面看到的图形不变,说明从前面看不到某位置上新放的小方块,据此得出添加的小方块应放在③号位置上。
【详解】如图:
在②号位置上面放一个同样的小方块,从左面看:
在③号位置上面放一个同样的小方块,从前面看:
填空如下:
在 ② 号位置上面放一个同样的小方块,从左面看到的图形不变,在 ③ 号位置上面放一个同样的小方块,从前面看到的图形不变。
6.
【分析】分子比分母小的分数叫作真分数;分子比分母大或分子和分母相等的分数叫作假分数;分子和分母只有公因数1,像这样的分数叫作最简分数;先按顺序列举出两个整数积为24的算式,再找出能组成最简真分数的两个数,即可求得。
【详解】1×24=24
2×12=24
3×8=24
4×6=24
分子、分母的积是24的最简真分数有和。
7. 10 78.5
【分析】把一个圆等分成若干份后拼成一个近似长方形,这个长方形的长是圆周长的一半,宽是圆的半径。
(1)求长方形的周长比圆的周长增加的部分:拼成后的长方形的周长比圆的周长多了圆的两个半径,据此计算即可。
(2)求长方形的面积:因为长方形的面积等于圆的面积,根据圆的面积公式S=πr2,即可求解。
【详解】(cm)
(cm2)
长方形的周长比原来圆的周长增加10cm,长方形的面积是78.5cm2。
8.(1)已行路程=总路程-剩下路程
(2)已行路程占总路程的几分之几
【分析】(1)从线段图可知,总路程是80千米,剩下总路程的。根据求一个数的几分之几是多少,用乘法解答,那么剩下的路程就是总路程80千米乘剩下路程占总路程的,即80×千米。根程80千米减去剩下的路程80×千米,据这个运算逻辑,其依据的等量关系就是:总路程一剩下的路程=已行的路程。
(2)把总路程看作单位“1”,已知剩下路程占总路程的,用1-这样得到的就是已行路程占总路程的几分之几。
乐乐列出的算式“80 ×(1-)”,就是用总路程80千米乘已行路程占总路程的分率(1-),从而求出已行的路程。
【详解】(1)由分析可知:小伍根据等量关系:已行路程=总路程-剩下路程可以列出算式“80-80×”。
(2)由分析可知:小娅列出算式为“80×(1-)”,其中“1-”表示的意义:已行路程占总路程的几分之几。
9.144
【分析】已知一件上衣原价250元,现价200元,用现价除以原价,求出现价是原价的百分之几;
已知买一条原价180元的裤子,把原价看作单位“1”,根据求一个数的百分之几是多少,用乘法计算,求出这条裤子的现价。
【详解】200÷250×100%
=0.8×100%
=80%
180×80%
=180×0.8
=144(元)
现价144元。
10. 37 (n2+1)
【分析】先观察前几个图形中圆的数量,尝试找出数量与图形序号之间的联系,进而得出第6个图形中圆的数量以及第n个图形中圆的数量的表达式。
【详解】第1个图形:有1+1=2个圆,这里前面的1可以看作是,即+1=2。
第2个图形:有4+1=5个圆,其中4恰好是,也就是+1=5。
第3个图形:有9+1=10个圆,9是,即+1=10。
第4个图形:有16+1=17个圆,16是,即+1=17。
……
第6个图形圆的个数有:+1=37(个)
发现规律:第n个图形中圆的数量是(+1)个。
填空如下:
所以第6个图形中有(37)个圆,第n个图形中有(+1)个圆。
11.D
【分析】已知一个小数,由6个十,即十位上是6;4个百分之一,即百分位上是4;其它数位上用0占位,据此写出这个小数。
【详解】一个小数,由6个十与4个百分之一组成,这个小数是60.04。
故答案为:D
12.C
【分析】正数、负数表示两种相反意义的量。如果规定向东走记作正,那么向西走就记作负。
【详解】如果规定向东走3m记作﹢3m,那么向西走2m可以记作﹣2m。
故答案为:C
13.C
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】亮亮调查了华南植物园各种植物的数量情况,如果要用统计图表示各种植物占植物总数的百分比,应选择(扇形统计图)。
故答案为:C
14.C
【分析】一台电视机打八五折出售,那么就是指现价比原价便宜(1-85%),求便宜多少元,利用原价乘便宜的折扣即可。
【详解】4800×(1-85%)
=4800×15%
=720(元)
所以便宜了720元。
因此正确的列式是4800×(1-85%)。
故答案为:C
15.B
【分析】根据题意,先用员工总人数减去今天请假的人数,求出今天出勤的人数;再根据“出勤率=出勤人数÷总人数×100%”,求出今天的出勤率。
【详解】(50-2)÷50×100%
=48÷50×100%
=0.96×100%
=96%
这个公司今天的出勤率是96%。
故答案为:B
16.C
【分析】根据题意,每月用水量6吨以内每吨2.5元,则每月6吨以内的水费是从0开始的一条线段;超过6吨的部分每吨3元,3大于2.5,超过6吨部分水费上升速度比6吨以内的要大,所以超过6吨部分的线段比6吨以内的线段要陡一些,据此找出能正确表示每月水费与用水量关系的折线统计图。
【详解】A.是一条从0开始的线段,表示水费的单价固定不变,不符合题意;
B.超过6吨部分的水费保持不变,不随用水量的增加而增加,不符合题意;
C.用水量超过6吨的线段比6吨以内的线段要陡,表示超过6吨的单价比6吨以内的单价要贵,符合题意;
D.折线的拐点在3吨,表示用水量超过3吨,单价上涨,不符合题意。
故答案为:C
17.C
【分析】根据“速度=路程÷时间”代入数据计算即可。
【详解】÷=×3=5(千米/小时)
所以小明步行的速度是5千米/小时。
故答案为:C
18.B
【分析】观察三个加法算式的得数相等,可以设它们的得数是1;根据“加数=和-一个加数”,求出、、的值,再比较大小即可。
分数大小的比较:分母相同时,分子越大,分数值就越大;分子相同时,分母越大,分数值反而越小。
【详解】设;
那么、、的关系是。
故答案为:B
19.B
【分析】三角形的内角和是180°,因三个内角的度数比是1∶2∶3,最大角就占了三角形内角和的,根据分数乘法的意义,算出最大角,即可判断是什么三角形。
【详解】180×
=180×
=90°
一个角是直角的三角形是直角三角形。
故答案为:B
20.B
【分析】先根据进率“1米=100厘米”把6米换算成600厘米,4.8米换算成480厘米;
在长600厘米、宽480厘米的地面上铺方砖,要求都用整块的方砖,且正好铺满,那么方砖的边长是600和480的公因数;
先把600和480分解质因数,把公有的相同质因数乘起来即是它们的最大公因数,再列举这个最大公因数的所有因数,即是600和480的公因数,从各选项中找出哪个数是600和480的公因数,即是方砖的边长。
【详解】6米=600厘米
4.8米=480厘米
600=2×2×2×3×5×5
480=2×2×2×2×2×3×5
600和480的最大公因数是:2×2×2×3×5=120
120的因数:1,2,3,4,5,6,8,10,12,15,20,24,30,40,60,120;
A.50不是600和480的公因数,所以边长为50厘米的方砖不能正好铺满;
B.60是600和480的公因数,所以边长为60厘米的方砖能正好铺满;
C.80不是600和480的公因数,所以边长为80厘米的方砖不能正好铺满;
D.100不是600和480的公因数,所以边长为100厘米的方砖不能正好铺满。
故答案为:B
21.;;9;;
7;;4;0.05
【解析】略
22.2.5;100000;
24;48
【分析】(1)根据减法的性质:一个数减去两个数的和,等于这个数依次减去这两个数。据此计算;
(2)根据乘法结合律进行计算;
(3)先算小括号里面的减法,再算中括号里面的乘法,最后算中括号外面的除法;
(4)先根据积不变的规律把转化为,再根据乘法分配律进行计算。
【详解】(1)6.53-(3.53+)
=6.53-3.53-
=3-
=3-0.5
=2.5
(2)25×32×125
=25×(4×8)×125
=(25×4)×(8×125)
=100×1000
=100000
(3)36÷[(-)×3]
=36÷[(-)×3]
=36÷[×3]
=36÷
=36×
=24
(4)2.25×4.8+77.5×0.48
=2.25×4.8+7.75×4.8
=(2.25+7.75)×4.8
=10×4.8
=48
23.x=85;x=8;x=40
【分析】首先根据等式的性质,两边同时减去1.5,然后两边再同时除以0.2(20%=0.2)即可;
首先把x-x=3.2化成0.4x=3.2,然后根据等式的性质,两边同时除以0.4即可;
首先根据比例的基本性质化简,可得x=42×,然后根据等式的性质,两边同时乘即可。
【详解】20%x+1.5=18.5
解:0.2x+1.5=18.5
0.2x+1.5-1.5=18.5-1.5
0.2x=17
0.2x÷0.2=17÷0.2
x=85
(2)x-x=3.2
解:x-0.6x=3.2
0.4x=3.2
0.4x÷0.4=3.2÷0.4
x=8
(3)42∶=x∶
解:x=42×
x=30
x×=30×
x=40
24.(1)(7,5)
(2)(3)(4)见详解
【分析】(1)用数对表示位置的方法:数对的第一个数字表示列,第二个数字表示行;据此用数对表示点O所在的位置。
(2)根据旋转的特征,将图形A以点O为中心顺时针旋转90度,点O位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形B。
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,找到图形A的各顶点关于对称轴l的对称点后,依次连接各点得到图形A的对称图形C。
(4)图形A按2∶1的比放大,即把图形A的每条边都扩大到原来的2倍,据此画出放大后的图形D。
【详解】(1)观察如图,点O所在的位置是(7,5)。
(2)将图形A以点O为中心顺时针旋转90度,得到图形B,如下图。
(3)以直线l为对称轴画出图形A的轴对称图形,得到图形C,如下图。
(4)放大后三角形的底:2×2=4
放大后三角形的高:3×2=6
则画一个底为4、高为6的三角形D,如下图。
25.锡580克;铜2900克
【分析】将比的前后项看成份数,鼎的质量÷总份数=一份数,一份数分别乘锡和铜的对应份数,即可求出锡和铜的质量。
【详解】3480÷(1+5)
=3480÷6
=580(克)
580×1=580(克)
580×5=2900(克)
答:含锡580克,铜2900克。
26.150千克
【分析】设线下平均每天销售量是x千克;把线下平均每天销售量看作单位“1”,线上平均每天销售量是线下的(1+520%),用线下平均每天销售量×(1+520%)=线上平均每天销售量,据此列方程:x×(1+520%)=930,解方程,即可解答。
【详解】解:设线下平均每天销售量是x千克。
x×(1+520%)=930
6.2x=930
x=930÷6.2
x=150
答:线下平均每天销售量是150千克。
27.0.3厘米
【分析】根据体积的意义可知,当把圆锥形铁块从容器中取出后,下降部分水的体积就等于这个圆锥形铁块的体积。
先根据圆锥的体积公式:V=πr2h,把数据代入公式求出圆锥形铁块的体积;
根据圆的面积公式,求出圆柱的底面积;再根据圆柱的高,用下降部分水的体积除以除以圆柱形容器的底面积,即可求出水面下降的高度。
【详解】×3.14×32×10÷[3.14×(20÷2)2]
=×3.14×9×10÷[3.14×102]
=×3.14×9×10÷[3.14×100]
=94.2÷314
=0.3(厘米)
答:这时水面的高度会下降0.3厘米。
28.(1)妙想
(2)淘气
(3)按第一轮的成绩进行排名的。优点:规则简便容易操作;缺点:不能准确反映三人的真实水平。(说法不唯一)
【分析】(1)先根据“平均数=数据和÷数据个数”,求出三人的平均成绩,再比较大小即可;
(2)分别比较出三轮成绩中9个数字的大小,看谁的单轮成绩最高即可;
(3)先确定是根据平均数还是单轮成绩确定了笑笑是本次冠军,然后分析这个规则的优缺点即可。
【详解】(1)(25+50+36)÷3
=111÷3
=37(个)
(45+48+30)÷3
=123÷3
=41(个)
(40+41+45)÷3
=126÷3
=42(个)
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36 37
笑笑 45 48 30 41
妙想 40 41 45 42
42个>41个>37个
答:按平均分排名,妙想获得第一名。
(2)25个<30个<36个<40个<41个<45个<48个<50个
答:按单轮成绩最高排名,淘气获得第一名。
(3)按单轮成绩最高排名,淘气获得第一名;按平均分排名,妙想获得第一名。
按第一轮成绩排名:25个<40个<45个,笑笑获得第一名;
按第二轮成绩排名:41个<48个<50个,淘气获得第一名;
按第三轮成绩排名:30个<36个<45个,妙想获得第一名;
由此可知:笑笑是本次冠军,是按第一轮的成绩进行排名的。
优点:规则简便容易操作;缺点:不能准确反映三人的真实水平。(说法不唯一)
29.(1)方式二
(2)15次
【分析】(1)分别计算出两种方式的实际钱数,比较即可。一年有12个月,方式一:单价×数量=总价,每月次数×月数=总次数,单价×总次数=实际钱数;方式二:每次另外收费钱数×总次数,然后再加上240元的会员费是实际钱数。
(2)两种方式,游泳次数相同,每次相差16元,240元里面有几个16元,就有几次。
【详解】(1)方式一:30×(12×2)
=30×24
=720(元)
方式二:240+14×(12×2)
=240+14×24
=240+336
=576(元)
720>576
答:他选择方式二更划算。
(2)240÷(30-14)
=240÷16
=15(次)
答:一年内游泳达到15次时,两种付费方式所用钱数相等。
30.1∶2
【分析】正六边形的内角和是720度,相当于两个圆的内角和,所以浅灰色部分的面积=一个小圆的面积+一个大圆的面积;那么外面深灰色部分面积=2个小圆的面积+2个大圆的面积;即外面深灰色部分面积=2×(一个小圆的面积+一个大圆的面积);所以面积比是1∶2;据此解答即可。
【详解】根据分析可得:
浅灰色部分的面积=一个小圆的面积+一个大圆的面积
深灰色部分面积=2个小圆的面积+2个大圆的面积=2×(一个小圆的面积+一个大圆的面积)=2×浅灰色部分的面积;
所以浅灰色部分与深灰色部分面积之比是1∶2。
【点睛】在求不规则图形面积时,往往利用割补结合:观察图形,把图形分割,再进行移补,形成一个容易求得的图形进行解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
