等腰三角形性质的应用
图片预览




文档简介
课件21张PPT。初中数学说课课件课题名称:
等腰三角形性质的应用 教学目标:
1、掌握等腰三角形的性质,并能灵活应用他们。并让学生获得“如何作辅助线”的体验
2、培养学生观察分析图形和发散思维解决问题的能力。
3、渗透对立统一,以不变应万变的辨证唯物主义思想方法和转化的数学思想。本节重点:
灵活掌握等腰三角形的性质
本节难点:
如何添加辅助线
复习:
1、等腰三角形的性质
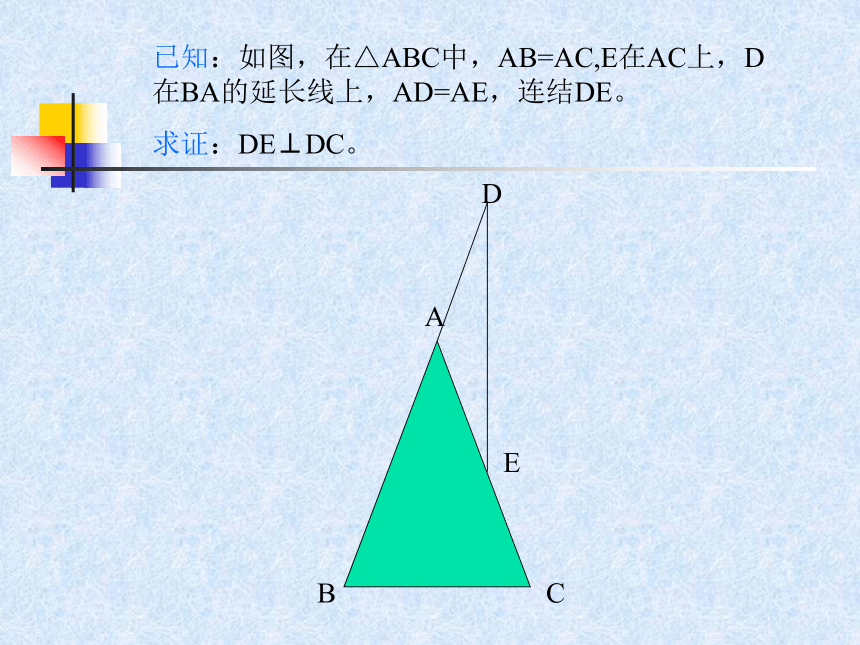
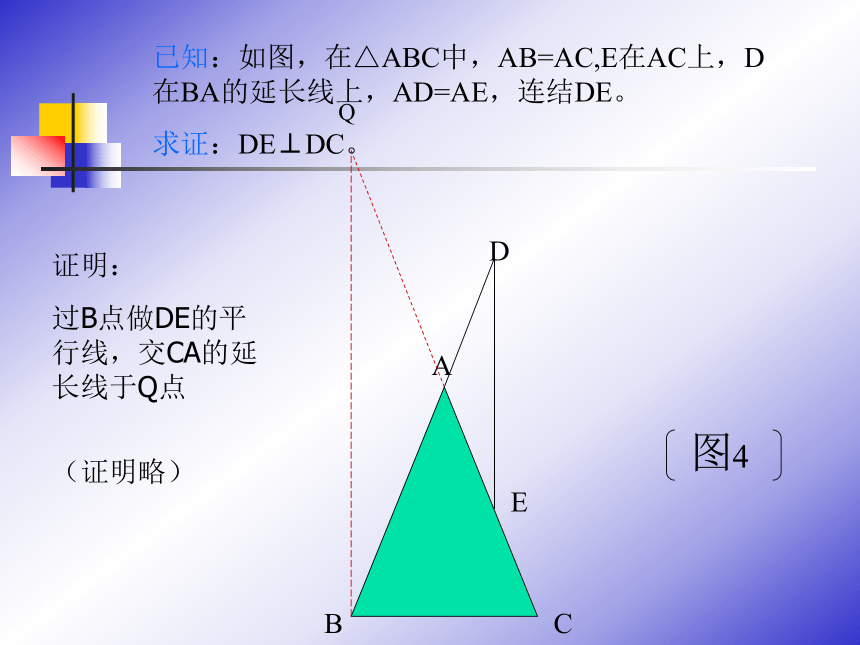
2、两条线段垂直的判断方法。 已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
延长DE交BC边于F点
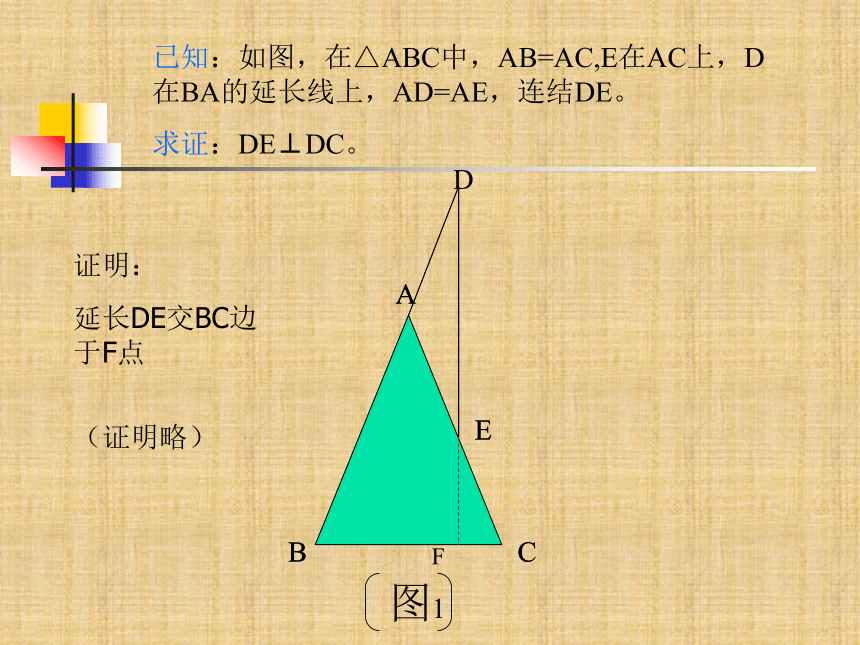
(证明略)NF已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过C点做AB的平行线,交DE的延长线于N点
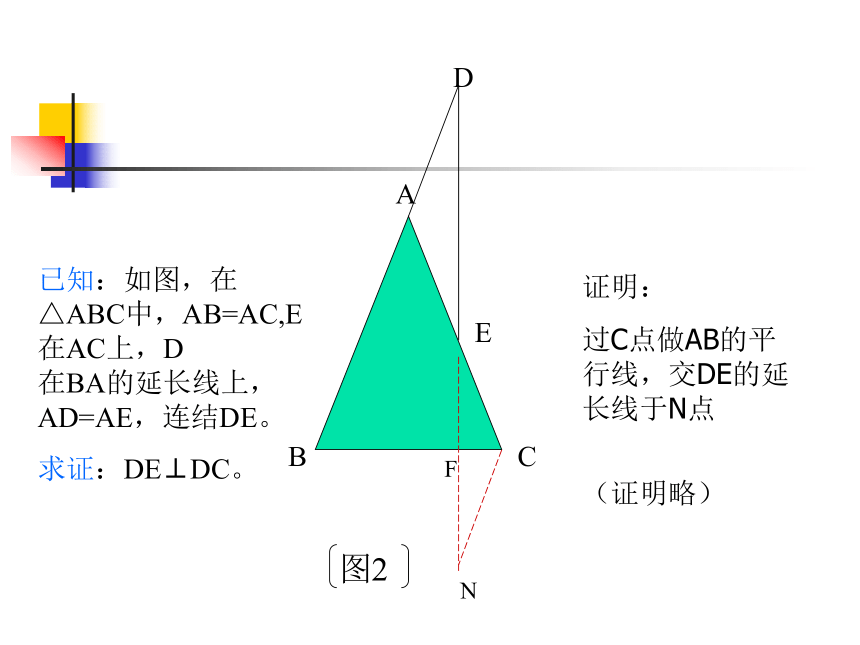
(证明略)GF已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过B点做AC的平行线,交DE的延长线于G点
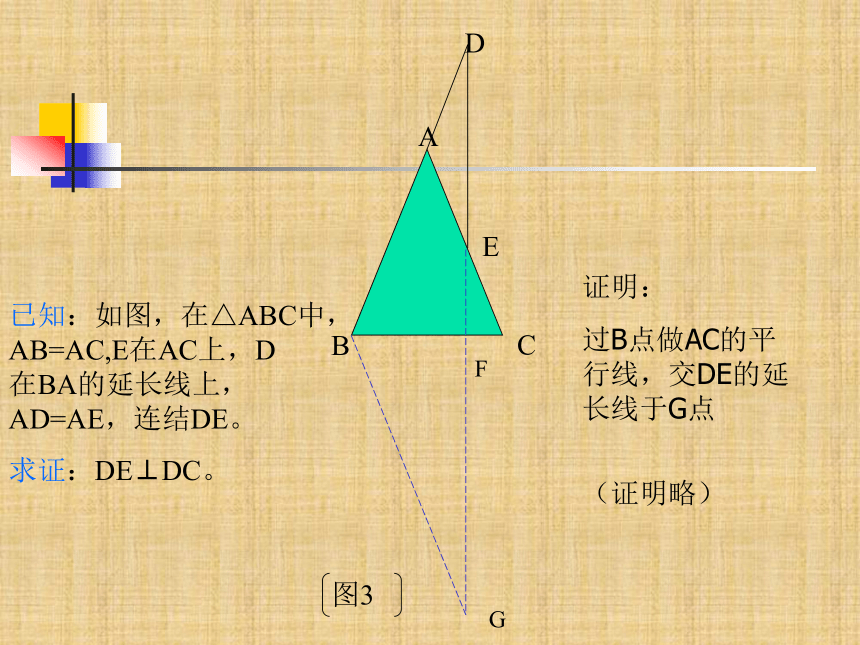
(证明略)Q图4已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过B点做DE的平行线,交CA的延长线于Q点
(证明略)图5R已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过C点做DE的平行线,交BA的延长线于R点
(证明略)FO已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过D点做BC的延长线,交CA的延长线于O点,并延长DE交BC于F点
(证明略)P图6已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过A点做BC的平行线,交DE于P点
(证明略)FK图7已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过E点做BC的平行线,交AB于K点,并延长DE交BC于F点
(证明略)MF图8 已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过E点做AB的平行线,交BC于M点,并延长DE交BC于F点
(证明略)FFH图9已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过D点做AC的平行线,交BC的延长线于H点,并延长DE交BC于F点
(证明略)已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过A点做DE的平行线,交BC于R点,并延长DE交BC于F点
(证明略)图中AR这条线段的引出可以看成是:
1、过A点做DE的平行线
2、过A点做BC的垂线
3、∠BAC的角平分线
4、BC边的中线ADD除了第一种辅助线的作法外,大部分同学能发现其余的辅助线都是作了AB的平行线,AC的平形线,BC的平行线和DE的平行线,。练习第一题已知,如图,AB=AC,BD⊥AC于D,求证:∠BAC=2∠DBC ABCD发散思考:此题是否可以通过加倍∠CBD,另作∠FBD=∠CBD? 已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延 长线上,且BD=CE,连结DE,交BC于F求证:DF=EF发散思考:如果把已知中的BD=CE与结论DF=EF互换,而其它条件不变,那此题是否成立?
谢谢莅临指导! 再见!
等腰三角形性质的应用 教学目标:
1、掌握等腰三角形的性质,并能灵活应用他们。并让学生获得“如何作辅助线”的体验
2、培养学生观察分析图形和发散思维解决问题的能力。
3、渗透对立统一,以不变应万变的辨证唯物主义思想方法和转化的数学思想。本节重点:
灵活掌握等腰三角形的性质
本节难点:
如何添加辅助线
复习:
1、等腰三角形的性质
2、两条线段垂直的判断方法。 已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
延长DE交BC边于F点
(证明略)NF已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过C点做AB的平行线,交DE的延长线于N点
(证明略)GF已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过B点做AC的平行线,交DE的延长线于G点
(证明略)Q图4已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过B点做DE的平行线,交CA的延长线于Q点
(证明略)图5R已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过C点做DE的平行线,交BA的延长线于R点
(证明略)FO已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过D点做BC的延长线,交CA的延长线于O点,并延长DE交BC于F点
(证明略)P图6已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过A点做BC的平行线,交DE于P点
(证明略)FK图7已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过E点做BC的平行线,交AB于K点,并延长DE交BC于F点
(证明略)MF图8 已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过E点做AB的平行线,交BC于M点,并延长DE交BC于F点
(证明略)FFH图9已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过D点做AC的平行线,交BC的延长线于H点,并延长DE交BC于F点
(证明略)已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。证明:
过A点做DE的平行线,交BC于R点,并延长DE交BC于F点
(证明略)图中AR这条线段的引出可以看成是:
1、过A点做DE的平行线
2、过A点做BC的垂线
3、∠BAC的角平分线
4、BC边的中线ADD除了第一种辅助线的作法外,大部分同学能发现其余的辅助线都是作了AB的平行线,AC的平形线,BC的平行线和DE的平行线,。练习第一题已知,如图,AB=AC,BD⊥AC于D,求证:∠BAC=2∠DBC ABCD发散思考:此题是否可以通过加倍∠CBD,另作∠FBD=∠CBD? 已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延 长线上,且BD=CE,连结DE,交BC于F求证:DF=EF发散思考:如果把已知中的BD=CE与结论DF=EF互换,而其它条件不变,那此题是否成立?
谢谢莅临指导! 再见!
