【课堂无忧】苏教版六下6.1《正比例的意义》(课件)
文档属性
| 名称 | 【课堂无忧】苏教版六下6.1《正比例的意义》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览






文档简介
(共41张PPT)
6.1
认识成正比例的量
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.经历从具体实例中认识成正比例的量的过程,初步理解正比例的意义,学会根据正比例的意义判断两种相关联的量是不是成正比例。
2.在认识成正比例的量的过程中,初步体会数量之间相依互变的关系,感受有效表示数量关系及其变化规律的不同数学模型,进一步培养观察能力和发现规律的能力。
3.进一步体会数学与日常生活的密切联系,增强从生活现象中探索数学知识和规律的意识。
看看谁答得又快又好。
已知路程和时间,怎样求速度?
路程÷时间=速度
已知总价和数量,怎样求单价?
总价÷数量=单价
已知工作总量和工作时间,怎样求工作效率?
工作总量÷工作时间=工作效率
02
新知导入
上面每组数量中,数量之间都存在着相依关系。当其中一个量变化时,另一个量也随着变化,而且这种变化是有规律的。
速度 = 路程÷时间
单价 = 总价÷数量
工作效率 = 工作总量÷工作时间
02
新知导入
03
任务一
学习任务一
正比例的意义
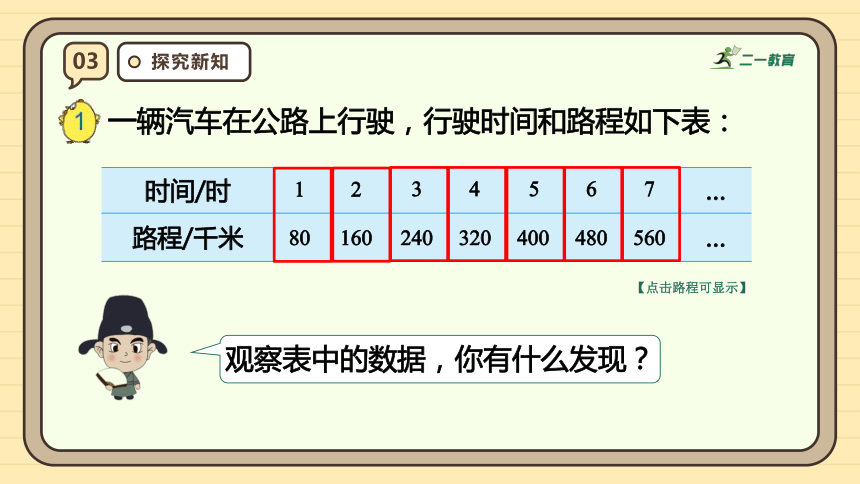
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
观察表中的数据,你有什么发现?
【点击路程可显示】
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
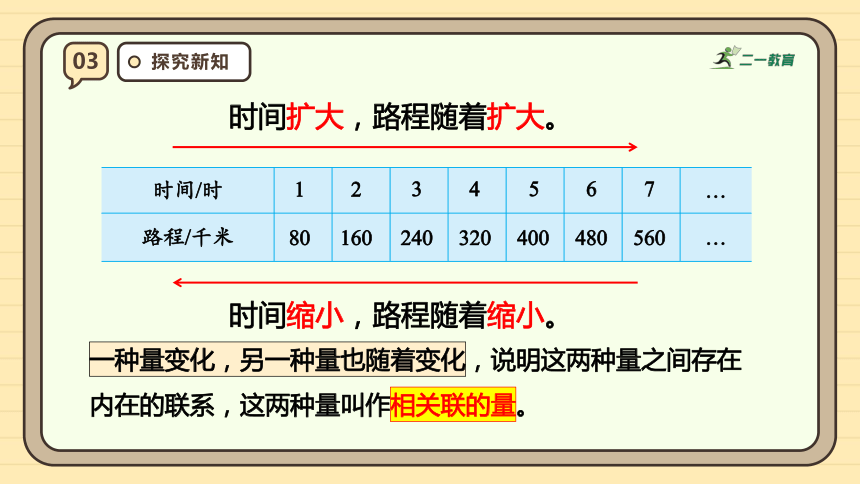
时间扩大,路程随着扩大。
时间缩小,路程随着缩小。
一种量变化,另一种量也随着变化,说明这两种量之间存在内在的联系,这两种量叫作相关联的量。
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
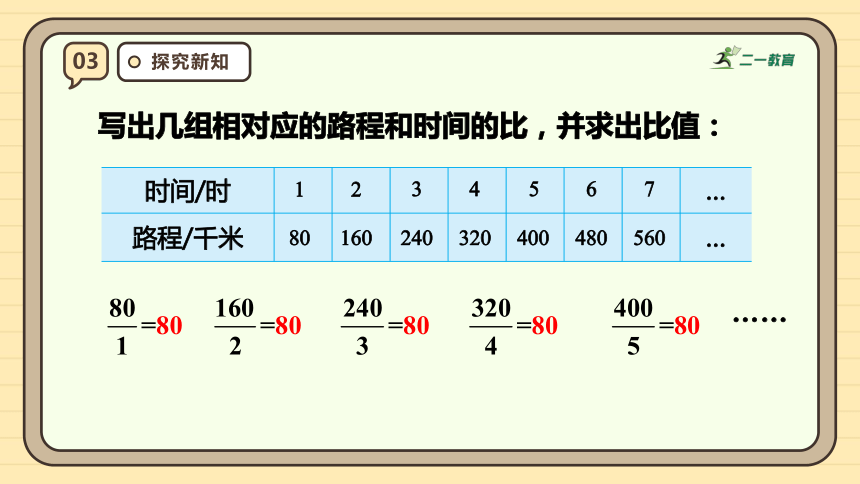
写出几组相对应的路程和时间的比,并求出比值:
……
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
你有什么发现?
……
相对应的路程和时间的比的比值都是80,
比值80,表示什么?
表示这辆汽车行驶的速度不变。
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
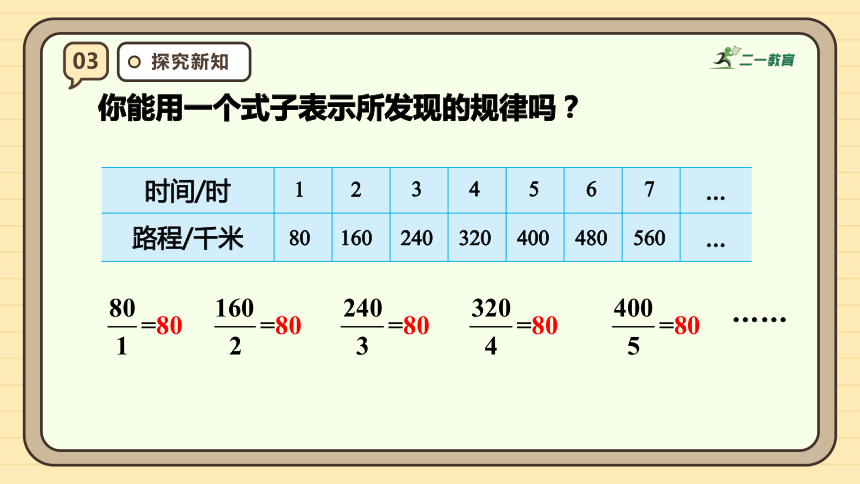
你能用一个式子表示所发现的规律吗?
……
03
探究新知
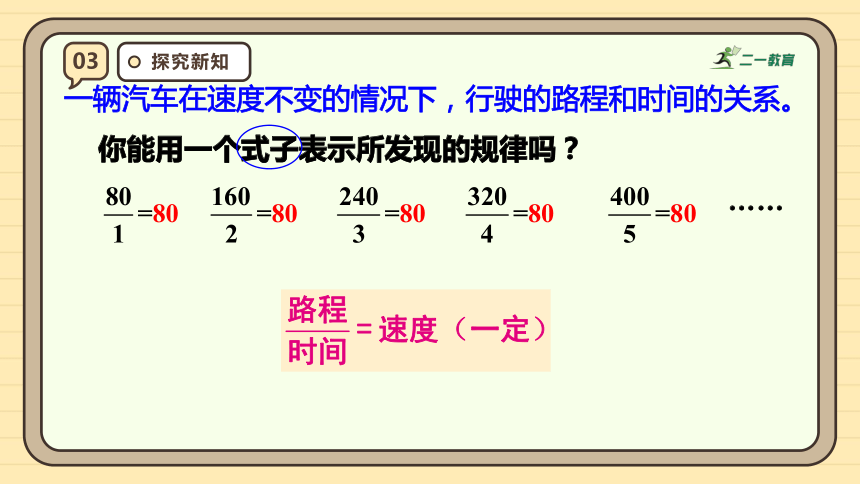
你能用一个式子表示所发现的规律吗?
……
一辆汽车在速度不变的情况下,行驶的路程和时间的关系。
03
探究新知
路程和时间是两种相关联的量,时间变化,路程也随着变化。
当路程和对应时间的比的比值总是一定时(也就是速度一定时),
行驶的路程和时间成正比例关系,行驶的路程和时间是成正比例的量。
正比例关系是表示相互依存的两种量之间的关系,不能只说某一种量成正比例关系。
03
探究新知
04
任务二
学习任务二
判断正比例关系
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(1)填写上表,
说说总价是随着哪个量的变化而变化的?
1.6
2.0
2.4
总价是随着数量的变化而变化的
铅笔单价为0.4元
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(2)你能写出几组相对应的总价和数量的比,并比较比值的大小吗?
1.6
2.0
2.4
比值相等
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(3)这个比值所表示的实际意义是什么?
1.6
2.0
2.4
(3)你能用式子表示它与总价、数量之间的关系吗?
这个比值表示铅笔的单价。
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(4)铅笔的总价和数量成正比例吗?为什么?
铅笔的总价和数量成正比例,因为铅笔的总价和数量是两种相关联的量,它们的比值是一定的。
1.6
2.0
2.4
04
探究新知
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
04
探究新知
它们的关系叫做正比例关系。
04
探究新知
判断两个量是否成正比例的关键是什么?
两个量是否成正比例,关键是它们是不是相关联的量,比值是否一定。
04
探究新知
如果用 x 和 y 表示两种相关联的量,用 k 表示它们的比值(一定),正比例关系可以用下面的式子表示:
(一定)
04
探究新知
正比例关系两种相关联的量的变化规律:
两种量同时扩大,同时缩小,比值不变。
生活中还有哪些成正比例的量?你能举例说一说吗?
05
拓展延伸
工作时间(时) 1 2 3 4 …
工作总量(根) 15 30 45 60 …
05
拓展延伸
面积(公顷) 1 2 3 4 5 …
总产量(千克) 12000 24000 36000 48000 60000 …
05
拓展延伸
时间(天) 1 2 3 4 …
总用量(立方米) 2 4 6 8 …
05
拓展延伸
判断两种量成正比例关系的方法:
(1)变化的两种量是相关的量;
(2)这两种量能写成比的形式;
(3)比值一定。
满足上述三种要求即成正比例关系。
正比例,很和气,两量相关要谨记。
同扩同缩默契好,比值一定不变异。
巧学妙记
05
拓展延伸
数量/个 1 2 3 4 5 6 …
总价/元 60 120 180
1.文具店卖出足球数量和总价如下表:
(1)把上表填写完整,说说总价是随着哪个量的变化而变化的。
(2)写出几组相对应的数量的比,并计较比值的大小。
240
300
360
60÷1=120÷2 =180÷3
----基础题
06
课堂练习
2.根据下表中底是6 cm的平行四边形的面积与高相对应的数据,判断它们是不是成正比例关系,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
成正比例关系
从表中可以明确地看出,平行四边形的面积随高的变化而变化,平行四边形的面积与高的比值不变,所以当平行四边形的底一定时,平行四边形的面积与高成正比例关系。
----基础题
06
课堂练习
请问总价与篮球的数量是不是成正比例关系, 如果成正比例关系, 在什么情况下呢
3.现在某体育用品店声称:如果买的篮球不超过50个,每个42元;如果买的篮球不少于50个,每个40元。
总价÷数量=单价,当单价一定时,总价与数量成正比例关系。
买的篮球不超过50个,单价固定为每个42元;买的篮球不少于50个,单价固定为每个40元。
成正比例关系
----基础题
06
课堂练习
4.填一填。
A×B=C(A,B,C均不为0)。
(1)当A一定时,( )和( )成( )比例。
(2)当B一定时,( )和( )成( )比例。
B
C
正
A
C
正
06
课堂练习----提高题
5. 在60米赛跑中,甲冲过终点线时,领先乙10米,
乙领先丙20米。假如乙和丙的速度始终不变,那
么乙到达终点时,将领先丙多少米?
解:设乙到终点时,丙跑的路程单位x米。
60:x=(60 10):(60 10 20)
x=36
60 36=24(米)
答:将领先丙24米。
06
课堂练习----拓展题
这节课你们都学会了哪些知识?
07
课堂小结
路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
=速度(一定)
路程
速度
1.彤彤把家里今年上半年的用水情况作了如下统计,已知每吨水的水费一定,请把表格填写完整。
月 份 1 2 3 4 5 6
用水量/吨 10 12 9 16
所交水费/元 31 40.3 43.4
37.2
27.9
13
14
49.6
08
作业布置
作业布置---知识技能类
2.东东和浩浩在400米的环形跑道上,背对背出发,已知东东和浩浩的速度比是2∶3,当他俩相遇时,东东走了多少米 浩浩呢
想:时间一定,路程和( )成正比例。
速度
东东:400× =160(米)
浩浩:400× =240(米)
2
2+3
3
2+3
08
作业布置
作业布置---知识技能类
3.如果 a= b(a,b≠0),那么a与b成正比例吗 为什么
成正比例。
2
3
5
6
a= b a∶b= ∶ =
a与b比值一定,成正比例。
2
3
5
6
5
6
2
3
5
4
08
作业布置
作业布置---知识技能类
4.体育课上正在进行百米赛跑。当李灵到达终点时,魏花在李灵后面20米处。如果她们各自的速度不变,要使两人同时到达终点,李灵的起点线应比原来后移多少米
解:设李灵的起跑线应比原来后移x 米。
(100+x)∶100=100∶(100-20)
x=25
答:李灵的起点线应比原来后移25米。
08
作业布置---选做题
08
作业布置---综合实践类作业
请找一找
在日常生活中找找成正比例的量。
09
板书设计
正比例的意义
路程和时间是两种相关联的量
路程和时间成正比例
(一定)
https://www.21cnjy.com/recruitment/home/fine
6.1
认识成正比例的量
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.经历从具体实例中认识成正比例的量的过程,初步理解正比例的意义,学会根据正比例的意义判断两种相关联的量是不是成正比例。
2.在认识成正比例的量的过程中,初步体会数量之间相依互变的关系,感受有效表示数量关系及其变化规律的不同数学模型,进一步培养观察能力和发现规律的能力。
3.进一步体会数学与日常生活的密切联系,增强从生活现象中探索数学知识和规律的意识。
看看谁答得又快又好。
已知路程和时间,怎样求速度?
路程÷时间=速度
已知总价和数量,怎样求单价?
总价÷数量=单价
已知工作总量和工作时间,怎样求工作效率?
工作总量÷工作时间=工作效率
02
新知导入
上面每组数量中,数量之间都存在着相依关系。当其中一个量变化时,另一个量也随着变化,而且这种变化是有规律的。
速度 = 路程÷时间
单价 = 总价÷数量
工作效率 = 工作总量÷工作时间
02
新知导入
03
任务一
学习任务一
正比例的意义
一辆汽车在公路上行驶,行驶时间和路程如下表:
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
观察表中的数据,你有什么发现?
【点击路程可显示】
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
时间扩大,路程随着扩大。
时间缩小,路程随着缩小。
一种量变化,另一种量也随着变化,说明这两种量之间存在内在的联系,这两种量叫作相关联的量。
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
写出几组相对应的路程和时间的比,并求出比值:
……
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
你有什么发现?
……
相对应的路程和时间的比的比值都是80,
比值80,表示什么?
表示这辆汽车行驶的速度不变。
03
探究新知
时间/时 …
路程/千米 …
1
80
2
160
240
320
400
480
560
3
4
5
6
7
你能用一个式子表示所发现的规律吗?
……
03
探究新知
你能用一个式子表示所发现的规律吗?
……
一辆汽车在速度不变的情况下,行驶的路程和时间的关系。
03
探究新知
路程和时间是两种相关联的量,时间变化,路程也随着变化。
当路程和对应时间的比的比值总是一定时(也就是速度一定时),
行驶的路程和时间成正比例关系,行驶的路程和时间是成正比例的量。
正比例关系是表示相互依存的两种量之间的关系,不能只说某一种量成正比例关系。
03
探究新知
04
任务二
学习任务二
判断正比例关系
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(1)填写上表,
说说总价是随着哪个量的变化而变化的?
1.6
2.0
2.4
总价是随着数量的变化而变化的
铅笔单价为0.4元
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(2)你能写出几组相对应的总价和数量的比,并比较比值的大小吗?
1.6
2.0
2.4
比值相等
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(3)这个比值所表示的实际意义是什么?
1.6
2.0
2.4
(3)你能用式子表示它与总价、数量之间的关系吗?
这个比值表示铅笔的单价。
04
探究新知
购买一种铅笔的数量和总价如下表:
数量/支 1 2 3 4 5 6 …
总价/元 0.4 0.8 1.2 …
(4)铅笔的总价和数量成正比例吗?为什么?
铅笔的总价和数量成正比例,因为铅笔的总价和数量是两种相关联的量,它们的比值是一定的。
1.6
2.0
2.4
04
探究新知
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量。
04
探究新知
它们的关系叫做正比例关系。
04
探究新知
判断两个量是否成正比例的关键是什么?
两个量是否成正比例,关键是它们是不是相关联的量,比值是否一定。
04
探究新知
如果用 x 和 y 表示两种相关联的量,用 k 表示它们的比值(一定),正比例关系可以用下面的式子表示:
(一定)
04
探究新知
正比例关系两种相关联的量的变化规律:
两种量同时扩大,同时缩小,比值不变。
生活中还有哪些成正比例的量?你能举例说一说吗?
05
拓展延伸
工作时间(时) 1 2 3 4 …
工作总量(根) 15 30 45 60 …
05
拓展延伸
面积(公顷) 1 2 3 4 5 …
总产量(千克) 12000 24000 36000 48000 60000 …
05
拓展延伸
时间(天) 1 2 3 4 …
总用量(立方米) 2 4 6 8 …
05
拓展延伸
判断两种量成正比例关系的方法:
(1)变化的两种量是相关的量;
(2)这两种量能写成比的形式;
(3)比值一定。
满足上述三种要求即成正比例关系。
正比例,很和气,两量相关要谨记。
同扩同缩默契好,比值一定不变异。
巧学妙记
05
拓展延伸
数量/个 1 2 3 4 5 6 …
总价/元 60 120 180
1.文具店卖出足球数量和总价如下表:
(1)把上表填写完整,说说总价是随着哪个量的变化而变化的。
(2)写出几组相对应的数量的比,并计较比值的大小。
240
300
360
60÷1=120÷2 =180÷3
----基础题
06
课堂练习
2.根据下表中底是6 cm的平行四边形的面积与高相对应的数据,判断它们是不是成正比例关系,并说明理由。
平行四边形的面积/cm2 6 12 18 24 30
平行四边形的高/cm 1 2 3 4 5
成正比例关系
从表中可以明确地看出,平行四边形的面积随高的变化而变化,平行四边形的面积与高的比值不变,所以当平行四边形的底一定时,平行四边形的面积与高成正比例关系。
----基础题
06
课堂练习
请问总价与篮球的数量是不是成正比例关系, 如果成正比例关系, 在什么情况下呢
3.现在某体育用品店声称:如果买的篮球不超过50个,每个42元;如果买的篮球不少于50个,每个40元。
总价÷数量=单价,当单价一定时,总价与数量成正比例关系。
买的篮球不超过50个,单价固定为每个42元;买的篮球不少于50个,单价固定为每个40元。
成正比例关系
----基础题
06
课堂练习
4.填一填。
A×B=C(A,B,C均不为0)。
(1)当A一定时,( )和( )成( )比例。
(2)当B一定时,( )和( )成( )比例。
B
C
正
A
C
正
06
课堂练习----提高题
5. 在60米赛跑中,甲冲过终点线时,领先乙10米,
乙领先丙20米。假如乙和丙的速度始终不变,那
么乙到达终点时,将领先丙多少米?
解:设乙到终点时,丙跑的路程单位x米。
60:x=(60 10):(60 10 20)
x=36
60 36=24(米)
答:将领先丙24米。
06
课堂练习----拓展题
这节课你们都学会了哪些知识?
07
课堂小结
路程和时间两个量,时间变化,所行驶的路程也随着变化,而且路程与时间的比值(也就是速度)一定,我们就说路程和时间成正比例。
=速度(一定)
路程
速度
1.彤彤把家里今年上半年的用水情况作了如下统计,已知每吨水的水费一定,请把表格填写完整。
月 份 1 2 3 4 5 6
用水量/吨 10 12 9 16
所交水费/元 31 40.3 43.4
37.2
27.9
13
14
49.6
08
作业布置
作业布置---知识技能类
2.东东和浩浩在400米的环形跑道上,背对背出发,已知东东和浩浩的速度比是2∶3,当他俩相遇时,东东走了多少米 浩浩呢
想:时间一定,路程和( )成正比例。
速度
东东:400× =160(米)
浩浩:400× =240(米)
2
2+3
3
2+3
08
作业布置
作业布置---知识技能类
3.如果 a= b(a,b≠0),那么a与b成正比例吗 为什么
成正比例。
2
3
5
6
a= b a∶b= ∶ =
a与b比值一定,成正比例。
2
3
5
6
5
6
2
3
5
4
08
作业布置
作业布置---知识技能类
4.体育课上正在进行百米赛跑。当李灵到达终点时,魏花在李灵后面20米处。如果她们各自的速度不变,要使两人同时到达终点,李灵的起点线应比原来后移多少米
解:设李灵的起跑线应比原来后移x 米。
(100+x)∶100=100∶(100-20)
x=25
答:李灵的起点线应比原来后移25米。
08
作业布置---选做题
08
作业布置---综合实践类作业
请找一找
在日常生活中找找成正比例的量。
09
板书设计
正比例的意义
路程和时间是两种相关联的量
路程和时间成正比例
(一定)
https://www.21cnjy.com/recruitment/home/fine
