【课堂无忧】苏教版六下6.3《反比例的意义》(课件)
文档属性
| 名称 | 【课堂无忧】苏教版六下6.3《反比例的意义》(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-08 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
6.3
反比例的意义
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.理解反比例的意义,能根据反比例的定义判断两种相关联的量是否成反比例。掌握反比例关系的数学表达式 x×y=k(一定)。
2.通过实例分析、数据对比,体会反比例关系中“一个量变化,另一个量随之反向变化”的规律。
3.感受数学与生活的密切联系,增强数学应用意识。培养合作探究精神和严谨的科学态度。
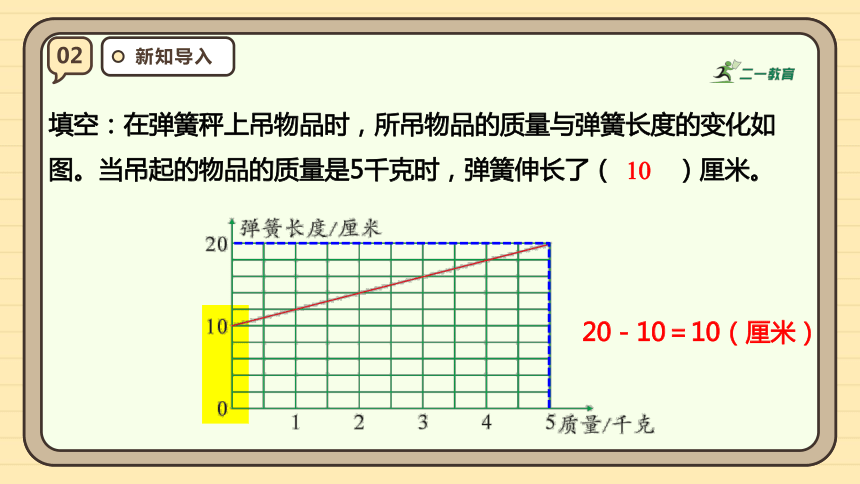
填空:在弹簧秤上吊物品时,所吊物品的质量与弹簧长度的变化如图。当吊起的物品的质量是5千克时,弹簧伸长了( )厘米。
20-10=10(厘米)
10
02
新知导入
03
任务一
学习任务一
反比例的意义
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
表中的两个量是怎样变化的?
这种变化有什么规律?
03
探究新知
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
(1)表中列出了哪两种相关联的量?它们分别是怎样变化的?
购买笔记本的数量随着单价的变化而变化。
单价和数量是两种相关联的量,单价变化,数量也随着变化。
03
探究新知
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
(2)题中两种量的变化有什么规律?可以用什么样的式子来表示?
越高
越少
越低
越多
笔记本的单价越低,购买的本数越多;
单价越高,购买的本数越少。
03
探究新知
一种量扩大,另一种量缩小。
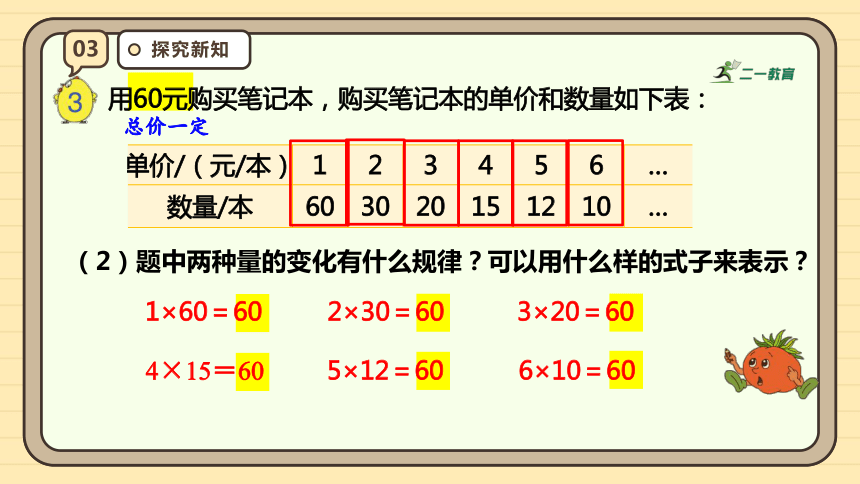
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
总价一定
(2)题中两种量的变化有什么规律?可以用什么样的式子来表示?
1×60=60
2×30=60
3×20=60
4×15=60
5×12=60
6×10=60
03
探究新知
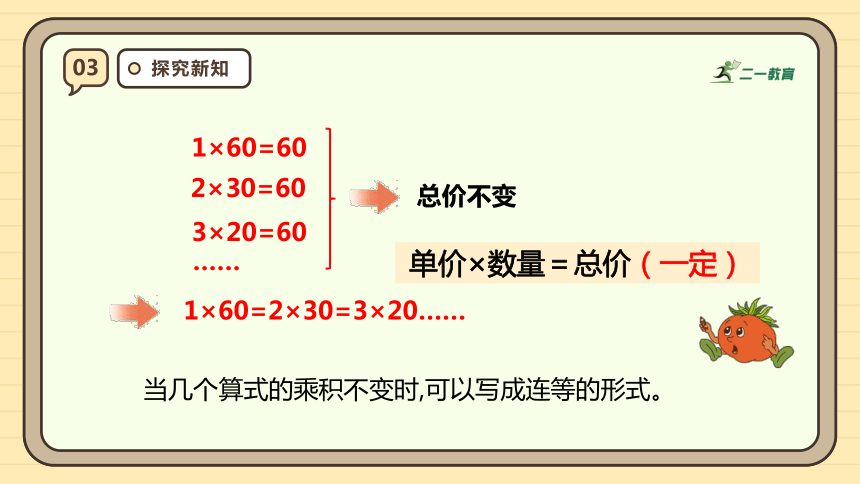
1×60=60
2×30=60
3×20=60
……
总价不变
1×60=2×30=3×20……
当几个算式的乘积不变时,可以写成连等的形式。
03
探究新知
单价×数量=总价(一定)
单价和数量是两种相关联的量,单价变化,数量也随着变化。当单价和数量的积总是一定(也就是总价一定)时,笔记本的单价和购买的数量成反比例关系,笔记本的单价和购买的数量是成反比例的量。
单价×数量=总价(一定)
03
探究新知
04
任务二
学习任务二
反比例的应用
生产240个零件,工作效率和工作时间如下表:
(1)填写上表,说说工作时间是随着哪个量的变化而变化的。
工作时间是随着工作效率的变化而变化的。
是指单位时间内完成的工作量。
工作效率/(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 …
5
6
04
探究新知
生产240个零件,工作效率和工作时间如下表:
(2)相对应的两个数的乘积各是多少?
工作效率/(个/本) 120 80 60 48 40 …
工作时间/时 2 3 4 …
48×5= 240
120×2=240
80×3=240
60×4=240
40×6=240
……
5
6
工作总量
(3)这个乘积表示的实际意义是什么?
04
探究新知
工作总量
生产240个零件,工作效率和工作时间如下表:
工作效率/(个/本) 120 80 60 48 40 …
工作时间/时 2 3 4 …
5
6
(3)你能用式子表示它与工作效率、工作时间之间的关系吗?
工作效率×工作时间=工作总量
(4)工作效率和工作时间成反比例吗? 为什么?
(一定)
工作效率和工作时间成反比例。
04
探究新知
如果用 x 和 y 表示两种相关联的量, 用 k 表示它们的积,反比例关系可以用下面的式子表示:
x × y = k (一定)
生活中还有哪些成反比例的量?你能举例说一说吗?
04
探究新知
速度×时间=路程
路程一定时,时间和速度成反比例;
长×宽=长方形面积
长方形面积一定时,长和宽成反比例;
······
05
拓展延伸
正比例与反比例有什么相同点和不同点?
正比例 反比例
相同点 不同点
都有两种相关联的量,且都有一个定量。
两种相关联的量同时扩大或缩小,而且相对应的两个数的比值(商)一定。
两种相关联的量一个扩大一个缩小,且相对应的两个数的积一定。
05
拓展延伸
判断两种量成反比例的方法:
(1)看变化的两种量是相关的量。
(2)这两种量能写成乘积的形式。
(3)乘积一定。满足上述三个要求即成反比例关系。
反比例,犟脾气,相关两量不默契。
你扩我缩来变化,乘积一定永不异。
巧学妙记
05
拓展延伸
反比例图像是光滑的曲线。
x × y = 60
05
拓展延伸
1.下面表格中的两个量是否成反比例?
(1) 输液时一小瓶葡萄糖均匀滴落时,每份滴与所需时间的关系如下:
每分滴数/滴 60 50 40 30 …
时间/分 20 24 30 40 ……
成反比例
----基础题
06
课堂练习
身高/cm 100 110 120 130 …
体重/kg 17 20 25 31 …
不成比例
(2)小明的身高与体重的关系如下:
(3)体积一定,圆柱体的底面积和高的关系如下:
底面积/dm2 300 200 150 120 100 …
高/dm 2 3 4 5 6 …
成反比例
----基础题
06
课堂练习
1.瓷砖面积一定, 砖的块数和铺地面积。
铺地面积÷砖的块数=每块瓷砖的面积(一定)
正比例
2.铺地面积一定,每块砖的面积和所需块数。
每块砖的面积×所需块数=铺地的面积。(一定)
反比例
3.铺地面积一定,每块砖的边长和所需块数。
不成比例
----基础题
06
课堂练习
2.下面两个量是否成比例?
3.填空。
(1)如果xy=8×7,那么x和y成( )比例。
(2)如果5a=6b(a,b均不为0),那么a和b成( )比例。
(3)在每块瓷砖面积,瓷砖的块数和总面积三个量中:
当每块瓷砖面积一定时,( )和( )成( )比例。
反
正
总面积
瓷砖的块数
正
----基础题
06
课堂练习
4.观察下表。
a 3 6
b 36
(1)若a和b成正比例,则 =( )。
(2)若a和b成反比例,则 =( )。
72
18
06
课堂练习----提高题
5. 一艘轮船往返甲、乙两个码头,去时顺水,每小时行20千米;返回时逆水,每小时行15千米,去时比返回少用了2小时。甲、乙两个码头相距多少千米?
解:设去时用了x小时。
20x=15(x+2)
x=6
20×6=120(千米)
答:甲、乙两个码头相距120千米。
06
课堂练习----拓展题
这节课你们都学会了哪些知识?
两种相关联的量,一种量变化,另一种量也随着变化。如果
这两种量中相对应的两个数的积一定,这两种量就叫作
成反比例的量,它们的关系叫作反比例关系。
用字母表示:x×y=k(一定)
07
课堂小结
1.判断正误。
(1)买书的总钱数一定,单价与数量成反比例。( )
(2)小明从家到学校,骑自行车的速度与时间成反比例。( )
(3)正方形的边长与面积成反比例。( )
(4)a×b=180中的a与b成反比例。 ( )
√
√
×
√
08
作业布置
作业布置---知识技能类
2.平行四边形的底和高如下表:
底/厘米 1 2 3 4 5 …
高/厘米 24 12 8 6 4.8 …
08
作业布置
作业布置---知识技能类
(1)表中的( )和( )是相关联的量,( )随着( )的
变化而变化。
(2)表中两个量相对应的乘积表示( ),
这个乘积是( )。
(3)因为平行四边形的高和底的( )一定,所以
平行四边形的高和底成( )比例。
底
高
高
底
平行四边形的面积
24平方厘米
乘积
反
08
作业布置
作业布置---知识技能类
3.已知 ×5= ×b(a,b≠0),a和b成不成比例 如果成,成什么比例
(1) ×5= ×b可整理为 = ,根据比例的基本性质可知( )×( )=( )×( )=( )。
(2)a和b的( )一定,所以a和b成( )。
乘积
5
b
a
b
5
6
30
反比例关系
08
作业布置
作业布置---知识技能类
1
a
1
6
1
a
1
6
( )
a
( )
6
4.有甲、乙、丙三个互相咬合的齿轮,当甲转2圈时,乙转3圈,丙转4圈,这三个齿轮的齿数比是多少
08
作业布置---选做题
时间一定时,转数与齿数成反比例。
2,3,4的最小公倍数是12(转过总数是相等的),
甲齿数∶乙齿数∶丙齿数= : : =6∶4∶3
12
2
12
3
12
4
08
作业布置---综合实践类作业
请找一找
在日常生活中找找成反比例的量。
09
板书设计
反比例的意义
单价×数量= 总价(一定)
单价和数量成反比例
x×y =k(一定) x和y成反比例
https://www.21cnjy.com/recruitment/home/fine
6.3
反比例的意义
(苏教版)六年级
下
01
教学目标
02
新知导入
03
任务一
04
任务二
05
拓展延伸
06
课堂练习
07
课堂小结
08
作业布置
09
板书设计
01
教学目标
1.理解反比例的意义,能根据反比例的定义判断两种相关联的量是否成反比例。掌握反比例关系的数学表达式 x×y=k(一定)。
2.通过实例分析、数据对比,体会反比例关系中“一个量变化,另一个量随之反向变化”的规律。
3.感受数学与生活的密切联系,增强数学应用意识。培养合作探究精神和严谨的科学态度。
填空:在弹簧秤上吊物品时,所吊物品的质量与弹簧长度的变化如图。当吊起的物品的质量是5千克时,弹簧伸长了( )厘米。
20-10=10(厘米)
10
02
新知导入
03
任务一
学习任务一
反比例的意义
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
表中的两个量是怎样变化的?
这种变化有什么规律?
03
探究新知
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
(1)表中列出了哪两种相关联的量?它们分别是怎样变化的?
购买笔记本的数量随着单价的变化而变化。
单价和数量是两种相关联的量,单价变化,数量也随着变化。
03
探究新知
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
(2)题中两种量的变化有什么规律?可以用什么样的式子来表示?
越高
越少
越低
越多
笔记本的单价越低,购买的本数越多;
单价越高,购买的本数越少。
03
探究新知
一种量扩大,另一种量缩小。
用60元购买笔记本,购买笔记本的单价和数量如下表:
单价/(元/本) 1 2 3 4 5 6 …
数量/本 60 30 20 15 12 10 …
总价一定
(2)题中两种量的变化有什么规律?可以用什么样的式子来表示?
1×60=60
2×30=60
3×20=60
4×15=60
5×12=60
6×10=60
03
探究新知
1×60=60
2×30=60
3×20=60
……
总价不变
1×60=2×30=3×20……
当几个算式的乘积不变时,可以写成连等的形式。
03
探究新知
单价×数量=总价(一定)
单价和数量是两种相关联的量,单价变化,数量也随着变化。当单价和数量的积总是一定(也就是总价一定)时,笔记本的单价和购买的数量成反比例关系,笔记本的单价和购买的数量是成反比例的量。
单价×数量=总价(一定)
03
探究新知
04
任务二
学习任务二
反比例的应用
生产240个零件,工作效率和工作时间如下表:
(1)填写上表,说说工作时间是随着哪个量的变化而变化的。
工作时间是随着工作效率的变化而变化的。
是指单位时间内完成的工作量。
工作效率/(个/时) 120 80 60 48 40 …
工作时间/时 2 3 4 …
5
6
04
探究新知
生产240个零件,工作效率和工作时间如下表:
(2)相对应的两个数的乘积各是多少?
工作效率/(个/本) 120 80 60 48 40 …
工作时间/时 2 3 4 …
48×5= 240
120×2=240
80×3=240
60×4=240
40×6=240
……
5
6
工作总量
(3)这个乘积表示的实际意义是什么?
04
探究新知
工作总量
生产240个零件,工作效率和工作时间如下表:
工作效率/(个/本) 120 80 60 48 40 …
工作时间/时 2 3 4 …
5
6
(3)你能用式子表示它与工作效率、工作时间之间的关系吗?
工作效率×工作时间=工作总量
(4)工作效率和工作时间成反比例吗? 为什么?
(一定)
工作效率和工作时间成反比例。
04
探究新知
如果用 x 和 y 表示两种相关联的量, 用 k 表示它们的积,反比例关系可以用下面的式子表示:
x × y = k (一定)
生活中还有哪些成反比例的量?你能举例说一说吗?
04
探究新知
速度×时间=路程
路程一定时,时间和速度成反比例;
长×宽=长方形面积
长方形面积一定时,长和宽成反比例;
······
05
拓展延伸
正比例与反比例有什么相同点和不同点?
正比例 反比例
相同点 不同点
都有两种相关联的量,且都有一个定量。
两种相关联的量同时扩大或缩小,而且相对应的两个数的比值(商)一定。
两种相关联的量一个扩大一个缩小,且相对应的两个数的积一定。
05
拓展延伸
判断两种量成反比例的方法:
(1)看变化的两种量是相关的量。
(2)这两种量能写成乘积的形式。
(3)乘积一定。满足上述三个要求即成反比例关系。
反比例,犟脾气,相关两量不默契。
你扩我缩来变化,乘积一定永不异。
巧学妙记
05
拓展延伸
反比例图像是光滑的曲线。
x × y = 60
05
拓展延伸
1.下面表格中的两个量是否成反比例?
(1) 输液时一小瓶葡萄糖均匀滴落时,每份滴与所需时间的关系如下:
每分滴数/滴 60 50 40 30 …
时间/分 20 24 30 40 ……
成反比例
----基础题
06
课堂练习
身高/cm 100 110 120 130 …
体重/kg 17 20 25 31 …
不成比例
(2)小明的身高与体重的关系如下:
(3)体积一定,圆柱体的底面积和高的关系如下:
底面积/dm2 300 200 150 120 100 …
高/dm 2 3 4 5 6 …
成反比例
----基础题
06
课堂练习
1.瓷砖面积一定, 砖的块数和铺地面积。
铺地面积÷砖的块数=每块瓷砖的面积(一定)
正比例
2.铺地面积一定,每块砖的面积和所需块数。
每块砖的面积×所需块数=铺地的面积。(一定)
反比例
3.铺地面积一定,每块砖的边长和所需块数。
不成比例
----基础题
06
课堂练习
2.下面两个量是否成比例?
3.填空。
(1)如果xy=8×7,那么x和y成( )比例。
(2)如果5a=6b(a,b均不为0),那么a和b成( )比例。
(3)在每块瓷砖面积,瓷砖的块数和总面积三个量中:
当每块瓷砖面积一定时,( )和( )成( )比例。
反
正
总面积
瓷砖的块数
正
----基础题
06
课堂练习
4.观察下表。
a 3 6
b 36
(1)若a和b成正比例,则 =( )。
(2)若a和b成反比例,则 =( )。
72
18
06
课堂练习----提高题
5. 一艘轮船往返甲、乙两个码头,去时顺水,每小时行20千米;返回时逆水,每小时行15千米,去时比返回少用了2小时。甲、乙两个码头相距多少千米?
解:设去时用了x小时。
20x=15(x+2)
x=6
20×6=120(千米)
答:甲、乙两个码头相距120千米。
06
课堂练习----拓展题
这节课你们都学会了哪些知识?
两种相关联的量,一种量变化,另一种量也随着变化。如果
这两种量中相对应的两个数的积一定,这两种量就叫作
成反比例的量,它们的关系叫作反比例关系。
用字母表示:x×y=k(一定)
07
课堂小结
1.判断正误。
(1)买书的总钱数一定,单价与数量成反比例。( )
(2)小明从家到学校,骑自行车的速度与时间成反比例。( )
(3)正方形的边长与面积成反比例。( )
(4)a×b=180中的a与b成反比例。 ( )
√
√
×
√
08
作业布置
作业布置---知识技能类
2.平行四边形的底和高如下表:
底/厘米 1 2 3 4 5 …
高/厘米 24 12 8 6 4.8 …
08
作业布置
作业布置---知识技能类
(1)表中的( )和( )是相关联的量,( )随着( )的
变化而变化。
(2)表中两个量相对应的乘积表示( ),
这个乘积是( )。
(3)因为平行四边形的高和底的( )一定,所以
平行四边形的高和底成( )比例。
底
高
高
底
平行四边形的面积
24平方厘米
乘积
反
08
作业布置
作业布置---知识技能类
3.已知 ×5= ×b(a,b≠0),a和b成不成比例 如果成,成什么比例
(1) ×5= ×b可整理为 = ,根据比例的基本性质可知( )×( )=( )×( )=( )。
(2)a和b的( )一定,所以a和b成( )。
乘积
5
b
a
b
5
6
30
反比例关系
08
作业布置
作业布置---知识技能类
1
a
1
6
1
a
1
6
( )
a
( )
6
4.有甲、乙、丙三个互相咬合的齿轮,当甲转2圈时,乙转3圈,丙转4圈,这三个齿轮的齿数比是多少
08
作业布置---选做题
时间一定时,转数与齿数成反比例。
2,3,4的最小公倍数是12(转过总数是相等的),
甲齿数∶乙齿数∶丙齿数= : : =6∶4∶3
12
2
12
3
12
4
08
作业布置---综合实践类作业
请找一找
在日常生活中找找成反比例的量。
09
板书设计
反比例的意义
单价×数量= 总价(一定)
单价和数量成反比例
x×y =k(一定) x和y成反比例
https://www.21cnjy.com/recruitment/home/fine
