山东省济南天桥区泺口实验学校2024-2025年第二学期八年级数学期中考试试题(含答案)
文档属性
| 名称 | 山东省济南天桥区泺口实验学校2024-2025年第二学期八年级数学期中考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 451.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 22:19:47 | ||
图片预览


文档简介
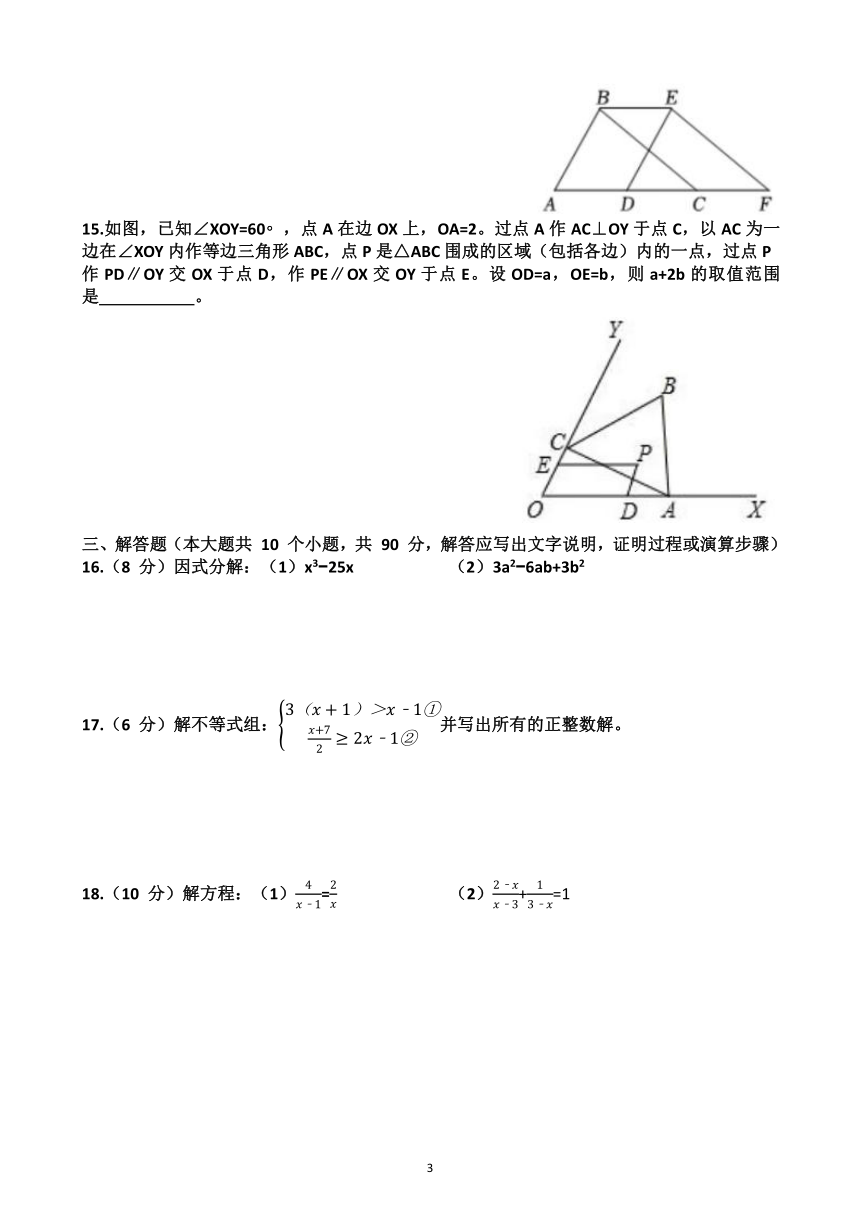
济南泺口实验学校 2024 - 2025 学年第二学期期中考试八年级数学试题(2025.04)
本试题分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分,共 4 页。满分 150 分,考试时间 120 分钟。答题前,请将学校、姓名、准考证号、座号写在答题卡规定的位置。
第 Ⅰ 卷(选择题 共 40 分)
一.单选题。(共10小题,每小题 4 分,共40分。在每小题给出的四个选项中,只有一个最符合题目要求。请将正确答案填入第 Ⅱ 卷相应的空格里。)
1.下列交通标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.若aA. a 3>b 3 B. 2a>2b C. 2 a>2 b D. >
3.若分式的值为0,则a的值为( )
4.A. 3 B. 0 C. 2 D. 2或 3
4.下列等式从左到右变形,属于因式分解的是( )
A. x(x+1)=x2+x B. (a+b)(a b)=a2 b2 C. x2 2x+1=(x 1)2 D. x2+6x+8=x(x+6)+8
5.已知线段CD是由线段AB平移得到的,点A( 1,3)平移后的对应点为C(2,2),则点B( 4,1)的对应点D的坐标为( )
A. ( 2,2) B. (1,5) C. ( 7,1) D. ( 1,0)
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AC=BD B. OA=OC C. AC⊥BD D. ∠ADC=∠BCD
7.如图,一次函数y1=ax+b(a,b为常数)与正比例函数y2=kx(k为常数)的图象交于点P( 4, 2),则关于x的不等式ax+b>kx的解集是( )
A. x> 2 B. x< 2 C. x> 4 D. x< 4
8.如图,等边△ABC中,D为BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转角等于( )
A. 18 B. 32 C. 60 D. 72
9.某中学八年级举行15km春季远足活动,两小组匀速前进,第一小组的步行速度是第二小组的1.2倍,第一小组比第二小组早0.7h到达目的地,求两个小组的步行速度。若设第二小组的步行速度为xkm/h,则可列出方程为( )
A. ﹣=0.7 B. ﹣=0.7 C. +=0.7 D. =﹣0.7
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①∠BAD=∠CAE;②△ABD △BCF;③四边形BDEF是平行四边形;④S△ABC= ;⑤S△ABD=2S△BCF,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分,把答案填在答题卡的横线上)
11.分解因式:mn+m2= 。
12.若代数式有意义,则实数x的取值范围是 。
13.如图,在平行四边形ABCD中,∠A=110 ,CE平分∠BCD,则∠DEC的度数是 。
14.如图,把△ABC沿着射线AC方向平移得到△DEF,BE=DC=2,则AF= 。
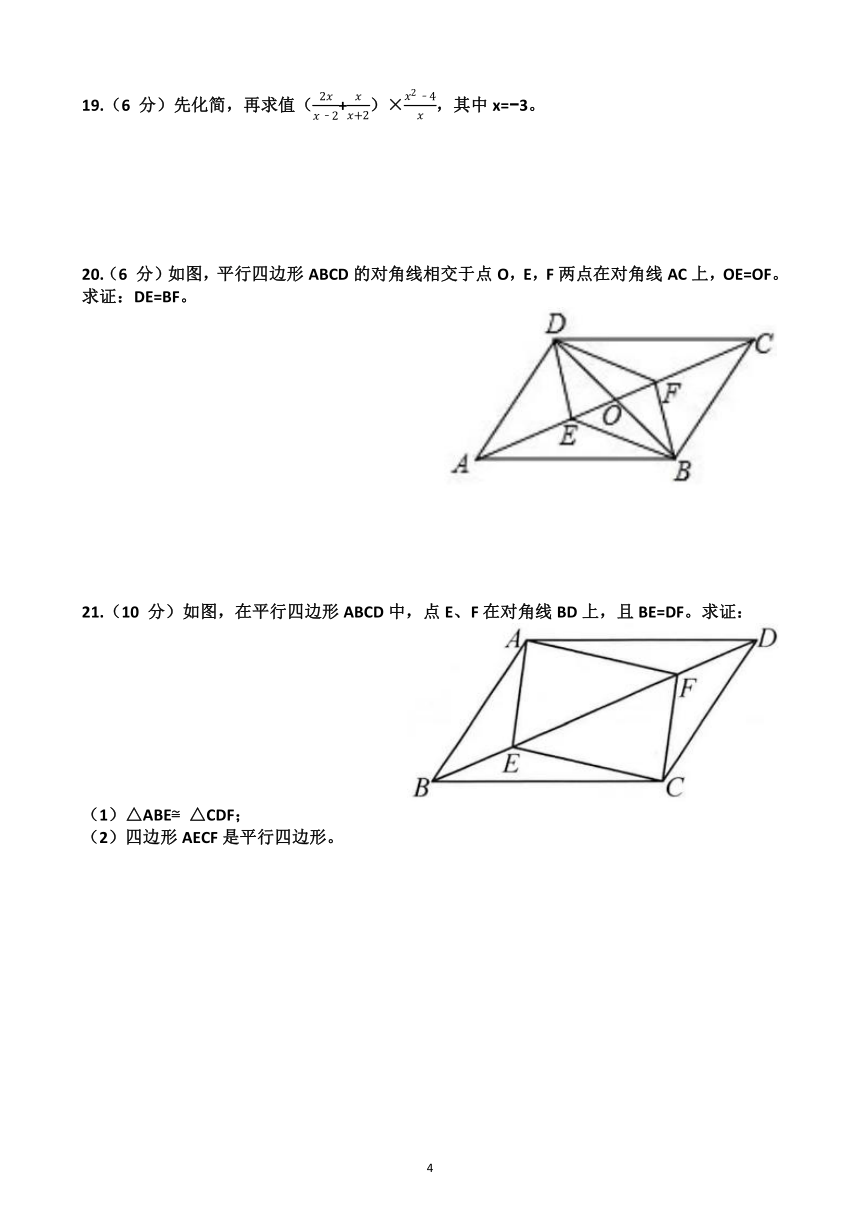
15.如图,已知∠XOY=60 ,点A在边OX上,OA=2。过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P
作PD∥OY交OX于点D,作PE∥OX交OY于点E。设OD=a,OE=b,则a+2b的取值范围是 。
三、解答题(本大题共 10 个小题,共 90 分,解答应写出文字说明,证明过程或演算步骤)
16.(8 分)因式分解:(1)x3 25x (2)3a2 6ab+3b2
17.(6 分)解不等式组:并写出所有的正整数解。
18.(10 分)解方程:(1)= (2)+=1
19.(6 分)先化简,再求值(+)×,其中x= 3。
20.(6 分)如图,平行四边形ABCD的对角线相交于点O,E,F两点在对角线AC上,OE=OF。求证:DE=BF。
21.(10 分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF。求证:
(1)△ABE △CDF;
(2)四边形AECF是平行四边形。
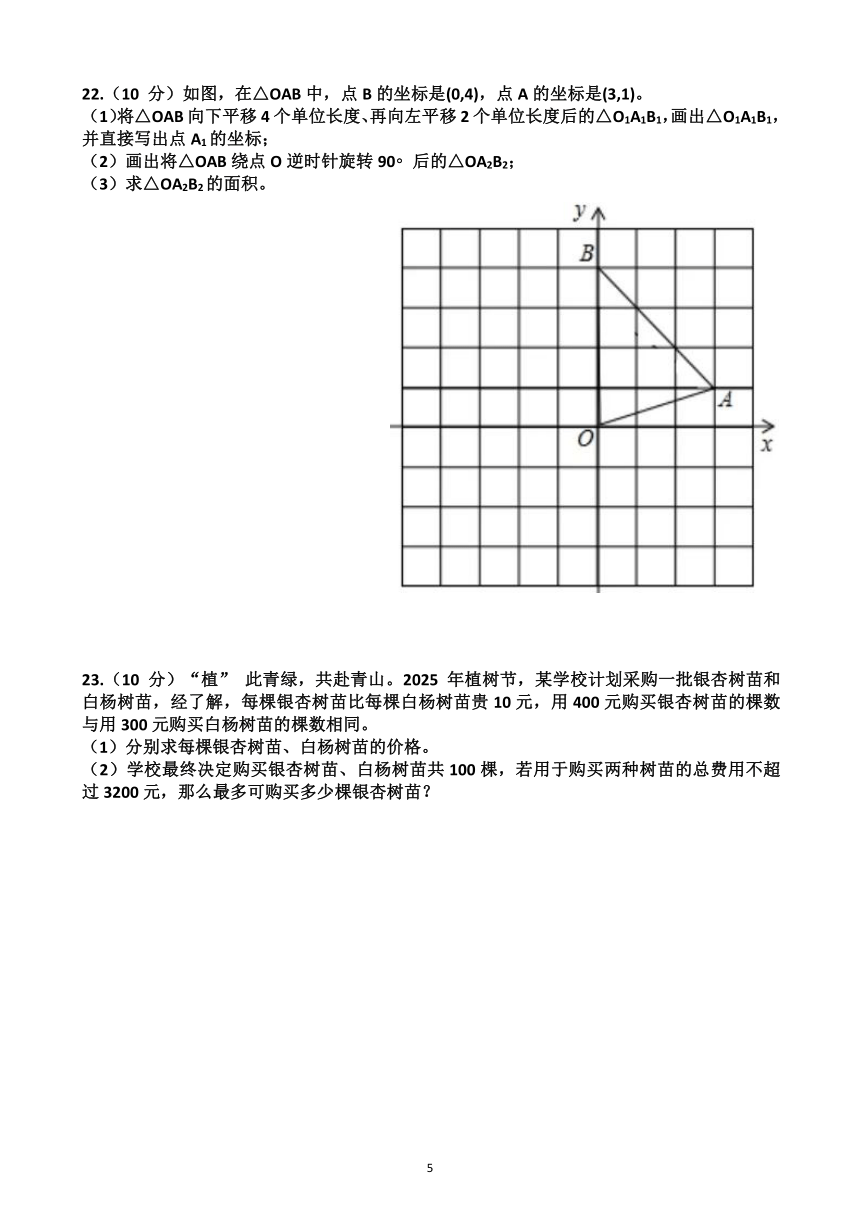
22.(10 分)如图,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1)。
(1)将△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标;
(2)画出将△OAB绕点O逆时针旋转90 后的△OA2B2;
(3)求△OA2B2的面积。
23.(10 分)“植” 此青绿,共赴青山。2025 年植树节,某学校计划采购一批银杏树苗和白杨树苗,经了解,每棵银杏树苗比每棵白杨树苗贵10元,用400元购买银杏树苗的棵数与用300元购买白杨树苗的棵数相同。
(1)分别求每棵银杏树苗、白杨树苗的价格。
(2)学校最终决定购买银杏树苗、白杨树苗共100棵,若用于购买两种树苗的总费用不超过3200元,那么最多可购买多少棵银杏树苗?
24.(12 分)在 “探究性学习” 小组的甲、乙两名同学所进行的因式分解:
甲:x2 xy+4x 4y =(x2 xy)+(4x 4y)(分成两组) =x(x y)+4(x y)(直接提公因式) =(x y)(x+4) 乙:a2 b2+c2+2bc =a2 (b2+c2 2bc)(分成两组) =a2 (b c)2(直接运用公式) =(a+b c)(a b+c)
请在他们的解法启发下解答下面各题:
(1)因式分解:a2+b2 9 2ab。
(2)若a b= 5,b c=3,求式子ab bc+ac a2的值。
(3)已知△ABC的三边a、b、c满足a2 b2 ac+bc=0,则△ABC为 三角形,并说明理由。
25.(12分)在等腰Rt△ABC中,∠BAC=90 ,以C为底角顶点作等腰Rt△CED,使∠CED=90 ,连接AD,分别以AB、AD为邻边作平行四边形ABFD,连接AF。
(1)如图 1,当点E在AC边上(不与点A、C重合),且点D在△ABC外部时,判断△AEF中,AE与EF的数量关系为______,位置关系为______;
(2)如图 2,将图 1 中△CED绕点C逆时针旋转,当点E落在线段BC上时,连接AE。求证:AF=AE;
(3)如图 3,将△CED绕点C继续逆时针旋转,当AD=AB,且△CED在△ABC的下方时,若AB=,CE=,求线段AE的长。
答案
一.单选题。(共10小题,每小题 4 分,共40分。在每小题给出的四个选项中,只有一个最符合题目要求。请将正确答案填入第 Ⅱ 卷相应的空格里。)
1.下列交通标志既是轴对称图形又是中心对称图形的是( D )
A. B. C. D.
2.若aA. a 3>b 3 B. 2a>2b C. 2 a>2 b D. >
3.若分式的值为0,则a的值为( C )
4.A. 3 B. 0 C. 2 D. 2或 3
4.下列等式从左到右变形,属于因式分解的是( C )
A. x(x+1)=x2+x B. (a+b)(a b)=a2 b2 C. x2 2x+1=(x 1)2 D. x2+6x+8=x(x+6)+8
5.已知线段CD是由线段AB平移得到的,点A( 1,3)平移后的对应点为C(2,2),则点B( 4,1)的对应点D的坐标为( D )
A. ( 2,2) B. (1,5) C. ( 7,1) D. ( 1,0)
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( B )
A. AC=BD B. OA=OC C. AC⊥BD D. ∠ADC=∠BCD
7.如图,一次函数y1=ax+b(a,b为常数)与正比例函数y2=kx(k为常数)的图象交于点P( 4, 2),则关于x的不等式ax+b>kx的解集是( D )
A. x> 2 B. x< 2 C. x> 4 D. x< 4
8.如图,等边△ABC中,D为BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转角等于( C )
A. 18 B. 32 C. 60 D. 72
9.某中学八年级举行15km春季远足活动,两小组匀速前进,第一小组的步行速度是第二小组的1.2倍,第一小组比第二小组早0.7h到达目的地,求两个小组的步行速度。若设第二小组的步行速度为xkm/h,则可列出方程为( A )
A. ﹣=0.7 B. ﹣=0.7 C. +=0.7 D. =﹣0.7
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①∠BAD=∠CAE;②△ABD △BCF;③四边形BDEF是平行四边形;④S△ABC= ;⑤S△ABD=2S△BCF,其中正确的有( B )
A. 2个 B. 3个 C. 4个 D. 5个
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分,把答案填在答题卡的横线上)
11.分解因式:mn+m2= m(n+m) 。
12.若代数式有意义,则实数x的取值范围是 x≠2 。
13.如图,在平行四边形ABCD中,∠A=110 ,CE平分∠BCD,则∠DEC的度数是 55° 。
14.如图,把△ABC沿着射线AC方向平移得到△DEF,BE=DC=2,则AF= 6 。
15.如图,已知∠XOY=60 ,点A在边OX上,OA=2。过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P
作PD∥OY交OX于点D,作PE∥OX交OY于点E。设OD=a,OE=b,则a+2b的取值范围是 2≤a+2b≤5 。
三、解答题(本大题共 10 个小题,共 90 分,解答应写出文字说明,证明过程或演算步骤)
16.(8 分)因式分解:(1)x3 25x (2)3a2 6ab+3b2
=x(x2﹣25) =3(a2 2ab+b2)
=x(x+5)(x﹣5) =3(a﹣b)2
17.(6 分)解不等式组:并写出所有的正整数解。
解不等式①得x>﹣2
解不等式②得x≤3
不等式组解集为﹣2<x≤3
正整数解为 1,2,3。
18.(10 分)解方程:(1)= (2)+=1
解(1)4x=2x﹣2
x=﹣1
经检验x=﹣1是原方程的根
(2)2﹣x﹣1=x﹣3
x=2
经检验x=2是原方程的根
19.(6 分)先化简,再求值(+)×,其中x= 3。
解原式=×
=3x+2
将x=﹣3代入得3×(﹣3)+2=﹣7
20.(6 分)如图,平行四边形ABCD的对角线相交于点O,E,F两点在对角线AC上,OE=OF。求证:DE=BF。
证明∵O是平行四边形ABCD对角线交点
∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形
∴DE=BF
21.(10 分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF。求证:
(1)△ABE △CDF;
(2)四边形AECF是平行四边形。
(1)∵四边形 ABCD 是平行四边形
∴AB//CD ,AB =CD
∴∠ABE=∠CDF
在△ABE 与△CDF中
∴△ABE≌△CDF ( SAS )
(2)由(1)知,△ABE≌△CDF
∴AE = CF ,∠AEB=∠CFD
∴∠AEF =180°-∠AEB=180°-∠CFD =∠CFE
∴AE // CF
∴四边形 AECF 是平行四边形
22.(10 分)如图,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1)。
(1)将△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标;
(2)画出将△OAB绕点O逆时针旋转90 后的△OA2B2;
(3)求△OA2B2的面积。
(2)如图
(3)4×3×=6
23.(10 分)“植” 此青绿,共赴青山。2025 年植树节,某学校计划采购一批银杏树苗和白杨树苗,经了解,每棵银杏树苗比每棵白杨树苗贵10元,用400元购买银杏树苗的棵数与用300元购买白杨树苗的棵数相同。
(1)分别求每棵银杏树苗、白杨树苗的价格。
(2)学校最终决定购买银杏树苗、白杨树苗共100棵,若用于购买两种树苗的总费用不超过3200元,那么最多可购买多少棵银杏树苗?
(1)设每棵银杏树苗的价格为 x 元,则每棵白杨树苗的价格为( x -10)元,
根据题意得:=
解得: x =40
经检验,x =40是原方程的解,且符合题意,
∴x -10=40-10=30
答:每棵银杏树苗的价格为40元,每棵白杨树苗的价格为30元;
设购买 m 棵银杏树苗,则购买(100- m)棵白杨树苗
根据题意得:40m+30x(100-m )≤3200
解得:m≤20
答:最多可购买20棵银杏树苗.
24.(12 分)在 “探究性学习” 小组的甲、乙两名同学所进行的因式分解:
甲:x2 xy+4x 4y =(x2 xy)+(4x 4y)(分成两组) =x(x y)+4(x y)(直接提公因式) =(x y)(x+4) 乙:a2 b2+c2+2bc =a2 (b2+c2 2bc)(分成两组) =a2 (b c)2(直接运用公式) =(a+b c)(a b+c)
请在他们的解法启发下解答下面各题:
(1)因式分解:a2+b2 9 2ab。
(2)若a b= 5,b c=3,求式子ab bc+ac a2的值。
(3)已知△ABC的三边a、b、c满足a2 b2 ac+bc=0,则△ABC为 三角形,并说明理由。
(1)=(a2+b2 2ab) 9
=(a﹣b)2﹣9
=(a﹣b+3)(a﹣b﹣3)
(2)=(ab﹣a2)+(ac﹣bc)
=a(b﹣a)﹣c(b﹣a)
=(b﹣a)(a﹣c)
将a b= 5,b c=3代入得﹣5×2=﹣10
(3)等腰
25.(12分)在等腰Rt△ABC中,∠BAC=90 ,以C为底角顶点作等腰Rt△CED,使∠CED=90 ,连接AD,分别以AB、AD为邻边作平行四边形ABFD,连接AF。
(1)如图 1,当点E在AC边上(不与点A、C重合),且点D在△ABC外部时,判断△AEF中,AE与EF的数量关系为______,位置关系为______;
(2)如图 2,将图 1 中△CED绕点C逆时针旋转,当点E落在线段BC上时,连接AE。求证:AF=AE;
(3)如图 3,将△CED绕点C继续逆时针旋转,当AD=AB,且△CED在△ABC的下方时,若AB=,CE=,求线段AE的长。
(1)AE=EF AE⊥EF
(2)连接EF,设DF交BC于点K
∵四边形 ABFD 是平行四边形,
∴AB // DF
∴∠DKE =∠ABC =45°
∴DE = EK ,∠EKF =180°-∠DKE =135°
∵∠ADE =180°-∠EDC =180°-45°=135°
∴∠EKF =∠ADE
∵∠DKC =∠C
∴DK = DC
∵DF = AB = AC
∴KF = AD
∴△EKF≌△EDA ( SAS )
∴EF = EA , ∠KEF =∠AED
∴∠FEA =∠BED =90°
∴△AEF 是等腰直角三角形,
∴AF =AE
(3)AE=3
本试题分第 Ⅰ 卷(选择题)和第 Ⅱ 卷(非选择题)两部分,共 4 页。满分 150 分,考试时间 120 分钟。答题前,请将学校、姓名、准考证号、座号写在答题卡规定的位置。
第 Ⅰ 卷(选择题 共 40 分)
一.单选题。(共10小题,每小题 4 分,共40分。在每小题给出的四个选项中,只有一个最符合题目要求。请将正确答案填入第 Ⅱ 卷相应的空格里。)
1.下列交通标志既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2.若a
3.若分式的值为0,则a的值为( )
4.A. 3 B. 0 C. 2 D. 2或 3
4.下列等式从左到右变形,属于因式分解的是( )
A. x(x+1)=x2+x B. (a+b)(a b)=a2 b2 C. x2 2x+1=(x 1)2 D. x2+6x+8=x(x+6)+8
5.已知线段CD是由线段AB平移得到的,点A( 1,3)平移后的对应点为C(2,2),则点B( 4,1)的对应点D的坐标为( )
A. ( 2,2) B. (1,5) C. ( 7,1) D. ( 1,0)
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AC=BD B. OA=OC C. AC⊥BD D. ∠ADC=∠BCD
7.如图,一次函数y1=ax+b(a,b为常数)与正比例函数y2=kx(k为常数)的图象交于点P( 4, 2),则关于x的不等式ax+b>kx的解集是( )
A. x> 2 B. x< 2 C. x> 4 D. x< 4
8.如图,等边△ABC中,D为BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转角等于( )
A. 18 B. 32 C. 60 D. 72
9.某中学八年级举行15km春季远足活动,两小组匀速前进,第一小组的步行速度是第二小组的1.2倍,第一小组比第二小组早0.7h到达目的地,求两个小组的步行速度。若设第二小组的步行速度为xkm/h,则可列出方程为( )
A. ﹣=0.7 B. ﹣=0.7 C. +=0.7 D. =﹣0.7
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①∠BAD=∠CAE;②△ABD △BCF;③四边形BDEF是平行四边形;④S△ABC= ;⑤S△ABD=2S△BCF,其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分,把答案填在答题卡的横线上)
11.分解因式:mn+m2= 。
12.若代数式有意义,则实数x的取值范围是 。
13.如图,在平行四边形ABCD中,∠A=110 ,CE平分∠BCD,则∠DEC的度数是 。
14.如图,把△ABC沿着射线AC方向平移得到△DEF,BE=DC=2,则AF= 。
15.如图,已知∠XOY=60 ,点A在边OX上,OA=2。过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P
作PD∥OY交OX于点D,作PE∥OX交OY于点E。设OD=a,OE=b,则a+2b的取值范围是 。
三、解答题(本大题共 10 个小题,共 90 分,解答应写出文字说明,证明过程或演算步骤)
16.(8 分)因式分解:(1)x3 25x (2)3a2 6ab+3b2
17.(6 分)解不等式组:并写出所有的正整数解。
18.(10 分)解方程:(1)= (2)+=1
19.(6 分)先化简,再求值(+)×,其中x= 3。
20.(6 分)如图,平行四边形ABCD的对角线相交于点O,E,F两点在对角线AC上,OE=OF。求证:DE=BF。
21.(10 分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF。求证:
(1)△ABE △CDF;
(2)四边形AECF是平行四边形。
22.(10 分)如图,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1)。
(1)将△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标;
(2)画出将△OAB绕点O逆时针旋转90 后的△OA2B2;
(3)求△OA2B2的面积。
23.(10 分)“植” 此青绿,共赴青山。2025 年植树节,某学校计划采购一批银杏树苗和白杨树苗,经了解,每棵银杏树苗比每棵白杨树苗贵10元,用400元购买银杏树苗的棵数与用300元购买白杨树苗的棵数相同。
(1)分别求每棵银杏树苗、白杨树苗的价格。
(2)学校最终决定购买银杏树苗、白杨树苗共100棵,若用于购买两种树苗的总费用不超过3200元,那么最多可购买多少棵银杏树苗?
24.(12 分)在 “探究性学习” 小组的甲、乙两名同学所进行的因式分解:
甲:x2 xy+4x 4y =(x2 xy)+(4x 4y)(分成两组) =x(x y)+4(x y)(直接提公因式) =(x y)(x+4) 乙:a2 b2+c2+2bc =a2 (b2+c2 2bc)(分成两组) =a2 (b c)2(直接运用公式) =(a+b c)(a b+c)
请在他们的解法启发下解答下面各题:
(1)因式分解:a2+b2 9 2ab。
(2)若a b= 5,b c=3,求式子ab bc+ac a2的值。
(3)已知△ABC的三边a、b、c满足a2 b2 ac+bc=0,则△ABC为 三角形,并说明理由。
25.(12分)在等腰Rt△ABC中,∠BAC=90 ,以C为底角顶点作等腰Rt△CED,使∠CED=90 ,连接AD,分别以AB、AD为邻边作平行四边形ABFD,连接AF。
(1)如图 1,当点E在AC边上(不与点A、C重合),且点D在△ABC外部时,判断△AEF中,AE与EF的数量关系为______,位置关系为______;
(2)如图 2,将图 1 中△CED绕点C逆时针旋转,当点E落在线段BC上时,连接AE。求证:AF=AE;
(3)如图 3,将△CED绕点C继续逆时针旋转,当AD=AB,且△CED在△ABC的下方时,若AB=,CE=,求线段AE的长。
答案
一.单选题。(共10小题,每小题 4 分,共40分。在每小题给出的四个选项中,只有一个最符合题目要求。请将正确答案填入第 Ⅱ 卷相应的空格里。)
1.下列交通标志既是轴对称图形又是中心对称图形的是( D )
A. B. C. D.
2.若a
3.若分式的值为0,则a的值为( C )
4.A. 3 B. 0 C. 2 D. 2或 3
4.下列等式从左到右变形,属于因式分解的是( C )
A. x(x+1)=x2+x B. (a+b)(a b)=a2 b2 C. x2 2x+1=(x 1)2 D. x2+6x+8=x(x+6)+8
5.已知线段CD是由线段AB平移得到的,点A( 1,3)平移后的对应点为C(2,2),则点B( 4,1)的对应点D的坐标为( D )
A. ( 2,2) B. (1,5) C. ( 7,1) D. ( 1,0)
6.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( B )
A. AC=BD B. OA=OC C. AC⊥BD D. ∠ADC=∠BCD
7.如图,一次函数y1=ax+b(a,b为常数)与正比例函数y2=kx(k为常数)的图象交于点P( 4, 2),则关于x的不等式ax+b>kx的解集是( D )
A. x> 2 B. x< 2 C. x> 4 D. x< 4
8.如图,等边△ABC中,D为BC上一点,△ABD经过旋转后到达△ACE的位置,则旋转角等于( C )
A. 18 B. 32 C. 60 D. 72
9.某中学八年级举行15km春季远足活动,两小组匀速前进,第一小组的步行速度是第二小组的1.2倍,第一小组比第二小组早0.7h到达目的地,求两个小组的步行速度。若设第二小组的步行速度为xkm/h,则可列出方程为( A )
A. ﹣=0.7 B. ﹣=0.7 C. +=0.7 D. =﹣0.7
10.如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中:①∠BAD=∠CAE;②△ABD △BCF;③四边形BDEF是平行四边形;④S△ABC= ;⑤S△ABD=2S△BCF,其中正确的有( B )
A. 2个 B. 3个 C. 4个 D. 5个
第 Ⅱ 卷(非选择题 共 110 分)
二、填空题(本大题共 5 个小题,每小题 4 分,共 20 分,把答案填在答题卡的横线上)
11.分解因式:mn+m2= m(n+m) 。
12.若代数式有意义,则实数x的取值范围是 x≠2 。
13.如图,在平行四边形ABCD中,∠A=110 ,CE平分∠BCD,则∠DEC的度数是 55° 。
14.如图,把△ABC沿着射线AC方向平移得到△DEF,BE=DC=2,则AF= 6 。
15.如图,已知∠XOY=60 ,点A在边OX上,OA=2。过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P
作PD∥OY交OX于点D,作PE∥OX交OY于点E。设OD=a,OE=b,则a+2b的取值范围是 2≤a+2b≤5 。
三、解答题(本大题共 10 个小题,共 90 分,解答应写出文字说明,证明过程或演算步骤)
16.(8 分)因式分解:(1)x3 25x (2)3a2 6ab+3b2
=x(x2﹣25) =3(a2 2ab+b2)
=x(x+5)(x﹣5) =3(a﹣b)2
17.(6 分)解不等式组:并写出所有的正整数解。
解不等式①得x>﹣2
解不等式②得x≤3
不等式组解集为﹣2<x≤3
正整数解为 1,2,3。
18.(10 分)解方程:(1)= (2)+=1
解(1)4x=2x﹣2
x=﹣1
经检验x=﹣1是原方程的根
(2)2﹣x﹣1=x﹣3
x=2
经检验x=2是原方程的根
19.(6 分)先化简,再求值(+)×,其中x= 3。
解原式=×
=3x+2
将x=﹣3代入得3×(﹣3)+2=﹣7
20.(6 分)如图,平行四边形ABCD的对角线相交于点O,E,F两点在对角线AC上,OE=OF。求证:DE=BF。
证明∵O是平行四边形ABCD对角线交点
∴OB=OD
∵OE=OF
∴四边形DEBF是平行四边形
∴DE=BF
21.(10 分)如图,在平行四边形ABCD中,点E、F在对角线BD上,且BE=DF。求证:
(1)△ABE △CDF;
(2)四边形AECF是平行四边形。
(1)∵四边形 ABCD 是平行四边形
∴AB//CD ,AB =CD
∴∠ABE=∠CDF
在△ABE 与△CDF中
∴△ABE≌△CDF ( SAS )
(2)由(1)知,△ABE≌△CDF
∴AE = CF ,∠AEB=∠CFD
∴∠AEF =180°-∠AEB=180°-∠CFD =∠CFE
∴AE // CF
∴四边形 AECF 是平行四边形
22.(10 分)如图,在△OAB中,点B的坐标是(0,4),点A的坐标是(3,1)。
(1)将△OAB向下平移4个单位长度、再向左平移2个单位长度后的△O1A1B1,画出△O1A1B1,并直接写出点A1的坐标;
(2)画出将△OAB绕点O逆时针旋转90 后的△OA2B2;
(3)求△OA2B2的面积。
(2)如图
(3)4×3×=6
23.(10 分)“植” 此青绿,共赴青山。2025 年植树节,某学校计划采购一批银杏树苗和白杨树苗,经了解,每棵银杏树苗比每棵白杨树苗贵10元,用400元购买银杏树苗的棵数与用300元购买白杨树苗的棵数相同。
(1)分别求每棵银杏树苗、白杨树苗的价格。
(2)学校最终决定购买银杏树苗、白杨树苗共100棵,若用于购买两种树苗的总费用不超过3200元,那么最多可购买多少棵银杏树苗?
(1)设每棵银杏树苗的价格为 x 元,则每棵白杨树苗的价格为( x -10)元,
根据题意得:=
解得: x =40
经检验,x =40是原方程的解,且符合题意,
∴x -10=40-10=30
答:每棵银杏树苗的价格为40元,每棵白杨树苗的价格为30元;
设购买 m 棵银杏树苗,则购买(100- m)棵白杨树苗
根据题意得:40m+30x(100-m )≤3200
解得:m≤20
答:最多可购买20棵银杏树苗.
24.(12 分)在 “探究性学习” 小组的甲、乙两名同学所进行的因式分解:
甲:x2 xy+4x 4y =(x2 xy)+(4x 4y)(分成两组) =x(x y)+4(x y)(直接提公因式) =(x y)(x+4) 乙:a2 b2+c2+2bc =a2 (b2+c2 2bc)(分成两组) =a2 (b c)2(直接运用公式) =(a+b c)(a b+c)
请在他们的解法启发下解答下面各题:
(1)因式分解:a2+b2 9 2ab。
(2)若a b= 5,b c=3,求式子ab bc+ac a2的值。
(3)已知△ABC的三边a、b、c满足a2 b2 ac+bc=0,则△ABC为 三角形,并说明理由。
(1)=(a2+b2 2ab) 9
=(a﹣b)2﹣9
=(a﹣b+3)(a﹣b﹣3)
(2)=(ab﹣a2)+(ac﹣bc)
=a(b﹣a)﹣c(b﹣a)
=(b﹣a)(a﹣c)
将a b= 5,b c=3代入得﹣5×2=﹣10
(3)等腰
25.(12分)在等腰Rt△ABC中,∠BAC=90 ,以C为底角顶点作等腰Rt△CED,使∠CED=90 ,连接AD,分别以AB、AD为邻边作平行四边形ABFD,连接AF。
(1)如图 1,当点E在AC边上(不与点A、C重合),且点D在△ABC外部时,判断△AEF中,AE与EF的数量关系为______,位置关系为______;
(2)如图 2,将图 1 中△CED绕点C逆时针旋转,当点E落在线段BC上时,连接AE。求证:AF=AE;
(3)如图 3,将△CED绕点C继续逆时针旋转,当AD=AB,且△CED在△ABC的下方时,若AB=,CE=,求线段AE的长。
(1)AE=EF AE⊥EF
(2)连接EF,设DF交BC于点K
∵四边形 ABFD 是平行四边形,
∴AB // DF
∴∠DKE =∠ABC =45°
∴DE = EK ,∠EKF =180°-∠DKE =135°
∵∠ADE =180°-∠EDC =180°-45°=135°
∴∠EKF =∠ADE
∵∠DKC =∠C
∴DK = DC
∵DF = AB = AC
∴KF = AD
∴△EKF≌△EDA ( SAS )
∴EF = EA , ∠KEF =∠AED
∴∠FEA =∠BED =90°
∴△AEF 是等腰直角三角形,
∴AF =AE
(3)AE=3
同课章节目录
