小升初复习精讲精练专题六《图形的认识与测量》 人教版(复习课件)(共37张PPT)
文档属性
| 名称 | 小升初复习精讲精练专题六《图形的认识与测量》 人教版(复习课件)(共37张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 10:36:53 | ||
图片预览





文档简介
(共37张PPT)
专题六:图形的认识与测量
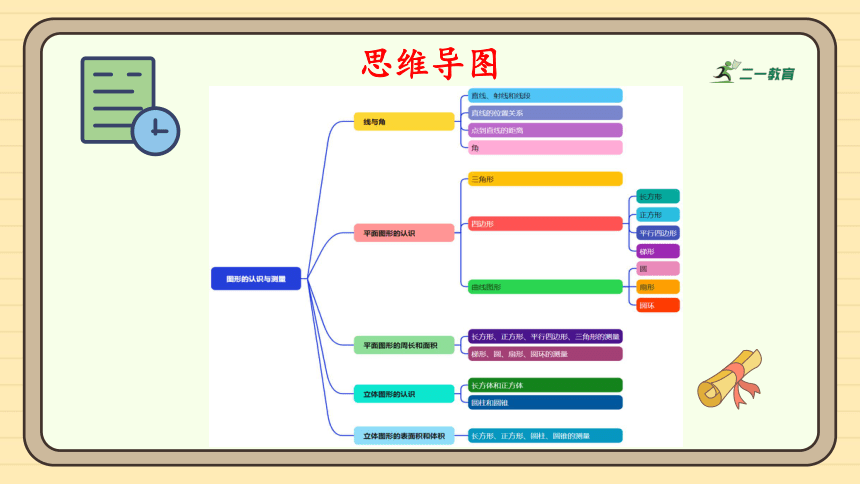
思维导图
01
线与角
知识清单
1、直线、射线和线段
(1)线段
①用直尺把两点连接起来,就得到一条线段。这两个点叫作线段的端点
②线段是直线的一部分,它有长短,可以度量
(2)直线
①把线段的两端无限延长,就得到一条直线
②直线没有端点,它可以向两边无限延长,不可以度量
(3)射线
①把线段的一端无限延长,就得到一条射线
②射线只有一个端点,它只能向一边无限延长,不可以度量
01
线与角
知识清单
2、直线的位置关系
(1)平行:在同一平面内不相交的两条直线叫作平行线。也可以说这两条直线互相平行
(2)相交:同一平面内不平行的两条直线一定相交
(3)垂直:两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足
3、点到直线的距离
①从直线外一点到这条直线所画的垂直线段的长度叫作这点到直线的距离
②从直线外一点向这条直线所画的所有线段中,垂线段最短;过直线外或直线上一点,有且只有一条直线与已知直线垂直
③平行线间的距离处处相等
01
线与角
知识清单
4、角
(1)角的意义:从一点引出两条射线所组成的图形叫作角。这个点叫作角的顶点,这两条射线叫作角的两条边。
(2)角的分类
a.锐角:大于0°而小于90°的角 b.直角:90°的角
c.钝角:大于90°而小于180°的角 d.平角:180°的角
e.周角:360°的角
(3)角的度量
用量角器量角的时候,要把量角器放在角的上面,使量角器的中心和角的顶点重合,0°刻度线和角的一条边重合,角的另一条边所对的刻度数就是这个角的度数。因为有内外两个刻度,读数时要注意沿着与角的一边重合的0°刻度线顺时针或逆时针读数。
02
平面图形的认识
知识清单
1、三角形
(1)分类
①按角分:直角三角形、钝角三角形、锐角三角形
②按边分:等腰三角形、等边三角形
(2)性质
①三角形的内角和:180°
②三角形的三边关系:任意两边之和大于第三边;任意两边之差小于第三边
③三角形的特性:具有稳定性
02
平面图形的认识
知识清单
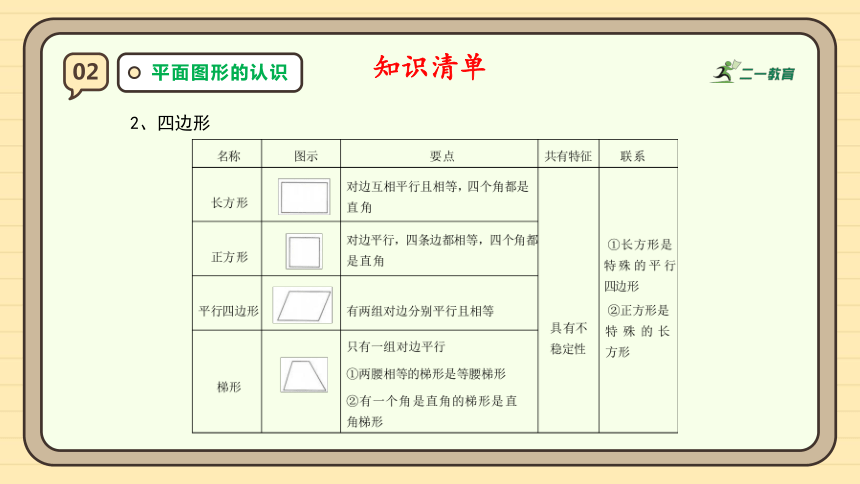
2、四边形
02
平面图形的认识
知识清单
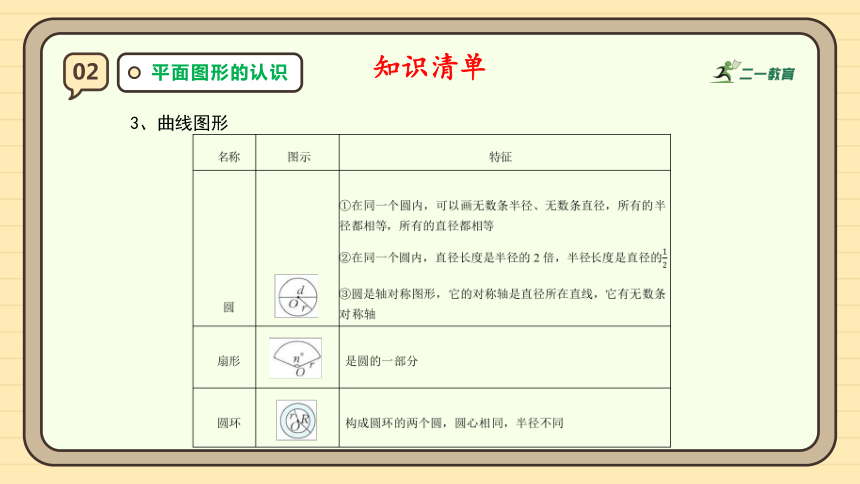
3、曲线图形
03
平面图形的周长和面积
知识清单
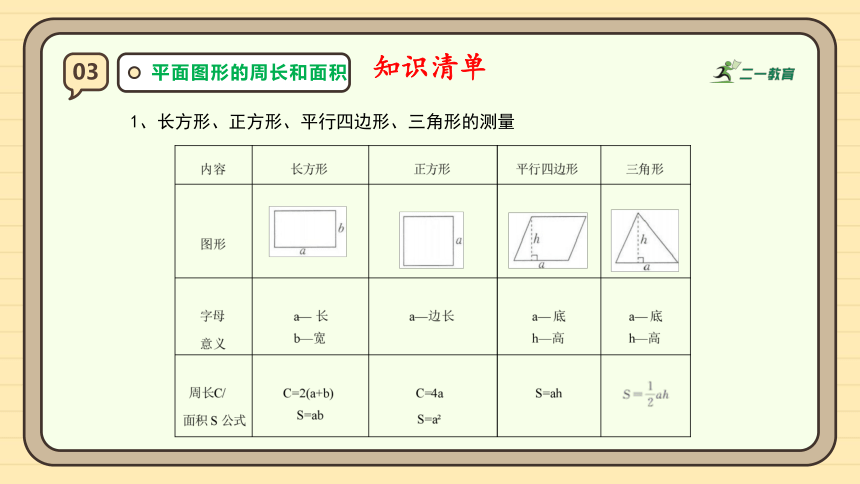
1、长方形、正方形、平行四边形、三角形的测量
03
平面图形的周长和面积
知识清单
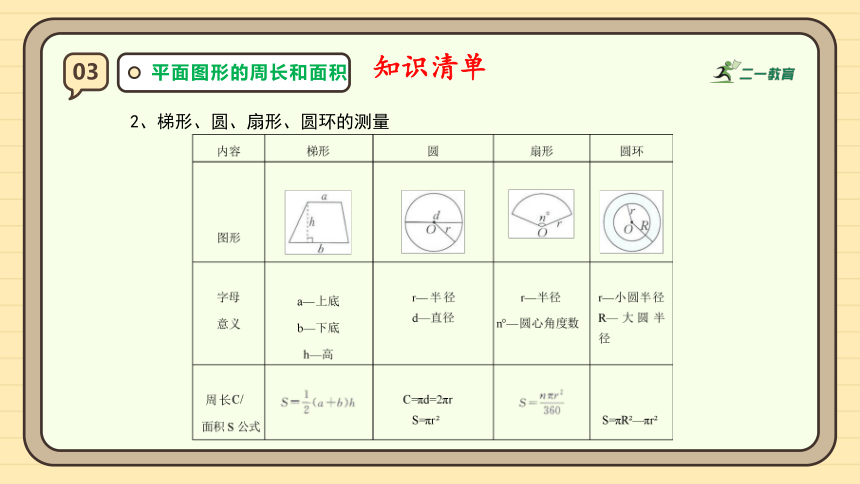
2、梯形、圆、扇形、圆环的测量
04
立体图形的认识
知识清单
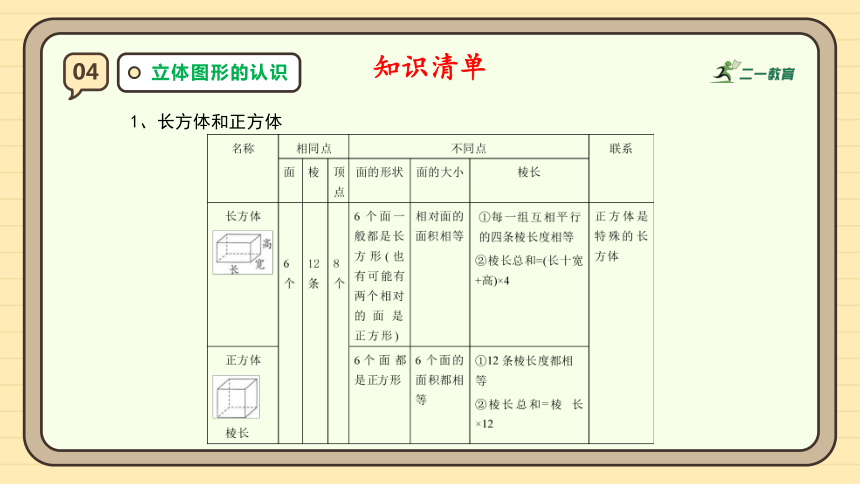
1、长方体和正方体
04
立体图形的认识
知识清单
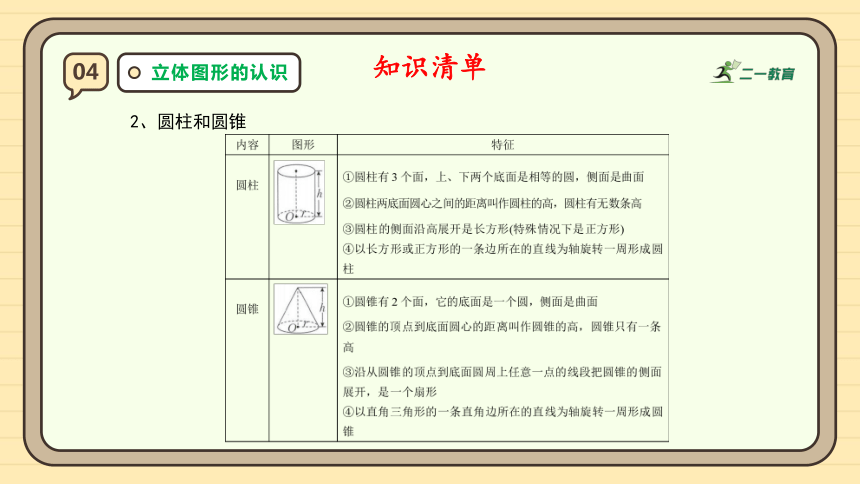
2、圆柱和圆锥
05
立体图形的表面积和体积
知识清单
1、长方形、正方形、圆柱、圆锥的测量
06
题型训练
例题精讲
01 线与角
1.丁丁在折纸,图( )中没有折出45°的角。
A. B. C. D.
【答案】B
【解答】根据分析:
A.正方形一个角对折后,也就是将90°角平均分成2份,一份为:90°÷2=45°,所以折出了45°的角;
B.折痕沿着六边形的中心平均分成了6份,一份为:360°÷6=60°,而六边形的每个角都不是直角,所以平均分成2份后,其中一个角并不会是45°,所以没有折出45°的角;
C.折痕沿着圆的中心平均分成了8份,一份为:360°÷8=45°,所以折出了45°的角;
D.三角形左下角是一个直角,将直角平均分成2份,一份为:90°÷2=45°,所以折出了45°的角。
故答案为:B
06
题型训练
例题精讲
01 线与角
2.如图所示,两条直线相交有1个交点,三条直线两两相交有3个交点,四条直线两两相交有6个交点……那么, 条直线两两相交有55个交点。
【答案】11
【解答】1=1
1+2=3
1+2+3=6
1+2+3+4=10
…
1+2+3+4+…+10=55
10+1=11
11条直线两两相交有55个交点。
06
题型训练
例题精讲
02 平面图形的认识
1.下图中,∠1=∠2,∠3=∠4,∠5=140°,那么∠A= °。
【答案】100
【解答】根据分析可知,
180°-140°=40°
180°-(40°+40°)
=180°-80°
=100°
∠A=100°
06
题型训练
例题精讲
02 平面图形的认识
2.下图中,左边的长方形与右边的四个图形随意交叉摆放,摆出重叠部分是四边形。当这个四边形一定是梯形时,应选择的图形是( )。当这个四边形一定是平行四边形时,应选择的图形是( )或( )。
【答案】② ① ③
【解答】三角形中没有两条边互相平行,因此当与长方形重叠摆出的这个四边形一定是梯形时,应选择的图形是三角形。长方形和平行四边形都有两组对边互相平行,因此当与长方形重叠摆出的这个四边形一定是平行四边形时,应选择的图形是长方形或平行四边形;
即题图中,左边的长方形与右边的四个图形随意交叉摆放,摆出重叠部分是四边形。当这个四边形一定是梯形时,应选择的图形是②。当这个四边形一定是平行四边形时,应选择的图形是①或③。
06
题型训练
例题精讲
02 平面图形的认识
3.一个长方形,其中三个角的顶点位置分别是(2,2)、(2,8)、(6,2)。
(1)请你在图中画出这个长方形。
(2)在上面画出的长方形中再画一个最大的圆,使所画的圆与这个长方形组成的组合图形只有1条对称轴。
【答案】
06
题型训练
例题精讲
03 平面图形的周长和面积
1.如图,小明将一个正方形纸剪出一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )。
A.16平方厘米 B.20平方厘米 C.80平方厘米 D.160平方厘米
【答案】C
【解答】解:设原正方形边长为x厘米。
5×(x-4)=4x
5x-20=4x
5x-4x-20=4x-4x
x-20=0
x-20+20=0+20
x=20
20×4=80(平方厘米)
一个长条面积为80平方厘米。
故答案为:C
06
题型训练
例题精讲
03 平面图形的周长和面积
2.有两张同样大小的长方形纸片,长10厘米,宽3厘米,把它们按图所示的方法叠合贴在一起,贴好后所成的“十”字图形,它的周长是 ,面积是 .
【答案】40厘米 51平方厘米
【解答】“十”字图形的周长为2个纸片,周长的和减去重叠部分正方形的周长,为(2×10+2×3)×2-4×3=40(厘米),“十”字图形的面积为2个纸片,面积的和减去重叠部分正方形的面积,为10×3×2-3×3=51(平方厘米)
06
题型训练
例题精讲
03 平面图形的周长和面积
3.如图,在一个梯形内有两个三角形的面积分别为10平方厘米和12平方厘米,已知梯形上、下底的比是2∶3,那么阴影部分的面积是多少平方厘米?
【答案】23平方厘米
【解答】假设上底为2厘米,下底为3厘米,
10×2÷2=10(厘米)
12×2÷3=8(厘米)
(2+3)×(10+8)÷2
=5×18÷2
=45(平方厘米)
45-10-12=23(平方厘米)
答:阴影部分面积是23平方厘米。
06
题型训练
例题精讲
04 立体图形的认识
1.礼品店要做一个长35厘米,宽25厘米,高15厘米的礼盒,用彩带按下图方法捆扎,接头处的彩带长20厘米。捆扎这个礼盒要用多少米长的彩带?(如图)
【答案】2米
【解答】35×2+25×2+15×4+20
=70+50+60+20
=120+60+20
=180+20
=200(厘米)
200厘米=2米
答:捆扎这个礼盒要用2米长的彩带。
06
题型训练
例题精讲
04 立体图形的认识
2.有一个正方体,每个面分别写上汉字:数、学、奥、林、匹、克。三个人从不同角度观察的结果如下图所示。这个正方体的每个汉字的对面各是什么字?
【答案】奥和克相对;林和学相对;数和匹相对
【解答】奥和克相对;
林和学相对;
数和匹相对;
答:奥和克相对;林和学相对;数和匹相对。
06
题型训练
例题精讲
05 立体图形的表面积和体积
1.长方体过同一顶点的三个面的面积分别是3、6、18,则这个长方体的体积是( )。
A.324 B.36 C.12 D.18
【答案】D
【解答】根据分析可知,长方体体积的平方=3×6×18
3×6×18=18×18
所以长方体体积为18。
故答案为:D
06
题型训练
例题精讲
05 立体图形的表面积和体积
2.求下面个圆柱的体积和表面积。(单位:cm)
【答案】体积56.52cm3;表面积99.81cm2
【解答】体积:3.14×32×8÷4
=226.08÷4
=56.52(立方厘米);
表面积:3.14×32÷2+3×8×2+3.14×3×2×8÷4
=14.13+48+37.68
=99.81(平方厘米)
07
专项训练
专项练习
1.工地上有一堆钢管,整体横截面是梯形,最上面一层有4根,最下面一层有8根,共堆放了5层,这堆钢管共有( )根。
2.一些棱长为4厘米的小正方体如图堆放在墙角处。
(1)这个物体露在外面的面有( )个。
(2)所有露在外面的面的面积是( )平方厘米。
30
17
272
07
专项训练
专项练习
3.如图,等边△ABC的边长是5,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,点A落在处,且点在△ABC外部,则阴影图形的周长等于( ).
4.对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=AB,则M是AB的中点;③若AM=AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AB的中点.其中正确的是( ).
15
②④
07
专项训练
专项练习
5.一个圆柱和一个圆锥,它们的底面积相等,高的比是2:1,它们的体积比是( ).
6.时钟指示2点15分,它的时针和分针所成的锐角是多少度?( )。
A.45度 B.30度 C.25度50分 D.22度30分
6:1
D
07
专项训练
专项练习
7.从一张长为3厘米,宽为2厘米的长方形纸中剪去一个直径为1厘米的圆(如下图)。下面( )最接近阴影部分的面积。
A.5平方厘米 B.4平方厘米 C.3平方厘米 D.2平方厘米
8.在下面的硬纸中,能折成一个正方体的是( )。
A. B. C. D.
B
A
07
专项训练
专项练习
9.下面四个图形中,阴影部分面积最小的是( ).
A. B. C. D.
10.如图,工地上有一堆沙子,近似于圆锥形。沙堆的体积是6m3,高为1.5m,这个沙堆的占地面积是( )。
A.24m2 B.12m2 C.8m2 D.4m2
C
B
07
专项训练
专项练习
11.小东测量瓶子的容积(如下图),测得瓶子的底面直径是10厘米,然后给瓶子内盛入一些水,正放时水高15厘米,倒放时水高25厘米,瓶子深30厘米。这个瓶子的容积是多少毫升?(π取3.14)(单位:厘米)
3.14×(10÷2)2×15+3.14×(10÷2)2×(30-25)
=3.14×25×15+3.14×25×5
=3.14×25×(15+5)
=78.5×20
=1570(立方厘米)
1570立方厘米=1570毫升
答:这个瓶子的容积是1570毫升。
07
专项训练
专项练习
12.下面是一个国际标准田径跑道的示意图.跑道的一周是多少米?
73×3.14+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
07
专项训练
专项练习
13.在一个等腰三角形中,有一个角是40°,求另外两个角的度数。
40°为顶角:
(180°-40°)÷2=70°
另外两个角的度数都是70°;
40°为一个底角:
180°-40°×2=100°
另外两个角的度数分别为40°、100°。
07
专项训练
专项练习
14.工人叔叔在粉刷教室,教室的长是9m,宽是8m,高是3.6m,门窗面积为21m ,要粉刷四周墙壁和顶棚.如果粉刷每平方米用环保漆300g,粉刷完这间教室共用环保漆多少千克?
9×8+9×3.6×2+8×3.6×2-21=173.4(m )
173.4×300=52020(g)=52.02(kg)
答:粉刷完这间教室共用环保漆52.02kg。
07
专项训练
专项练习
15.如图,ABCD是直角梯形,ACFE是长方形,已知BC-AD=4cm,CD=6cm,梯形面积是60cm2,求阴影部分的面积.
根据梯形的面积公式可知,(BC + AD)×CD÷2=60,所以BC + AD=20,又BC-AD=4,可求得BC=12(cm),AD=8(cm)
因为三角形ACD的面积=AC×CF÷2,而长方形ACFE的面积等于AC×CF,因此三角形ACD的面积等于阴影部分的面积,三角形ACD面积=AD×CD÷2=8×6÷2=24(cm2),因此阴影部分面积为24cm2.
答:阴影部分面积为24cm2。
https://www.21cnjy.com/recruitment/home/fine
专题六:图形的认识与测量
思维导图
01
线与角
知识清单
1、直线、射线和线段
(1)线段
①用直尺把两点连接起来,就得到一条线段。这两个点叫作线段的端点
②线段是直线的一部分,它有长短,可以度量
(2)直线
①把线段的两端无限延长,就得到一条直线
②直线没有端点,它可以向两边无限延长,不可以度量
(3)射线
①把线段的一端无限延长,就得到一条射线
②射线只有一个端点,它只能向一边无限延长,不可以度量
01
线与角
知识清单
2、直线的位置关系
(1)平行:在同一平面内不相交的两条直线叫作平行线。也可以说这两条直线互相平行
(2)相交:同一平面内不平行的两条直线一定相交
(3)垂直:两条直线相交成直角时,这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,这两条直线的交点叫作垂足
3、点到直线的距离
①从直线外一点到这条直线所画的垂直线段的长度叫作这点到直线的距离
②从直线外一点向这条直线所画的所有线段中,垂线段最短;过直线外或直线上一点,有且只有一条直线与已知直线垂直
③平行线间的距离处处相等
01
线与角
知识清单
4、角
(1)角的意义:从一点引出两条射线所组成的图形叫作角。这个点叫作角的顶点,这两条射线叫作角的两条边。
(2)角的分类
a.锐角:大于0°而小于90°的角 b.直角:90°的角
c.钝角:大于90°而小于180°的角 d.平角:180°的角
e.周角:360°的角
(3)角的度量
用量角器量角的时候,要把量角器放在角的上面,使量角器的中心和角的顶点重合,0°刻度线和角的一条边重合,角的另一条边所对的刻度数就是这个角的度数。因为有内外两个刻度,读数时要注意沿着与角的一边重合的0°刻度线顺时针或逆时针读数。
02
平面图形的认识
知识清单
1、三角形
(1)分类
①按角分:直角三角形、钝角三角形、锐角三角形
②按边分:等腰三角形、等边三角形
(2)性质
①三角形的内角和:180°
②三角形的三边关系:任意两边之和大于第三边;任意两边之差小于第三边
③三角形的特性:具有稳定性
02
平面图形的认识
知识清单
2、四边形
02
平面图形的认识
知识清单
3、曲线图形
03
平面图形的周长和面积
知识清单
1、长方形、正方形、平行四边形、三角形的测量
03
平面图形的周长和面积
知识清单
2、梯形、圆、扇形、圆环的测量
04
立体图形的认识
知识清单
1、长方体和正方体
04
立体图形的认识
知识清单
2、圆柱和圆锥
05
立体图形的表面积和体积
知识清单
1、长方形、正方形、圆柱、圆锥的测量
06
题型训练
例题精讲
01 线与角
1.丁丁在折纸,图( )中没有折出45°的角。
A. B. C. D.
【答案】B
【解答】根据分析:
A.正方形一个角对折后,也就是将90°角平均分成2份,一份为:90°÷2=45°,所以折出了45°的角;
B.折痕沿着六边形的中心平均分成了6份,一份为:360°÷6=60°,而六边形的每个角都不是直角,所以平均分成2份后,其中一个角并不会是45°,所以没有折出45°的角;
C.折痕沿着圆的中心平均分成了8份,一份为:360°÷8=45°,所以折出了45°的角;
D.三角形左下角是一个直角,将直角平均分成2份,一份为:90°÷2=45°,所以折出了45°的角。
故答案为:B
06
题型训练
例题精讲
01 线与角
2.如图所示,两条直线相交有1个交点,三条直线两两相交有3个交点,四条直线两两相交有6个交点……那么, 条直线两两相交有55个交点。
【答案】11
【解答】1=1
1+2=3
1+2+3=6
1+2+3+4=10
…
1+2+3+4+…+10=55
10+1=11
11条直线两两相交有55个交点。
06
题型训练
例题精讲
02 平面图形的认识
1.下图中,∠1=∠2,∠3=∠4,∠5=140°,那么∠A= °。
【答案】100
【解答】根据分析可知,
180°-140°=40°
180°-(40°+40°)
=180°-80°
=100°
∠A=100°
06
题型训练
例题精讲
02 平面图形的认识
2.下图中,左边的长方形与右边的四个图形随意交叉摆放,摆出重叠部分是四边形。当这个四边形一定是梯形时,应选择的图形是( )。当这个四边形一定是平行四边形时,应选择的图形是( )或( )。
【答案】② ① ③
【解答】三角形中没有两条边互相平行,因此当与长方形重叠摆出的这个四边形一定是梯形时,应选择的图形是三角形。长方形和平行四边形都有两组对边互相平行,因此当与长方形重叠摆出的这个四边形一定是平行四边形时,应选择的图形是长方形或平行四边形;
即题图中,左边的长方形与右边的四个图形随意交叉摆放,摆出重叠部分是四边形。当这个四边形一定是梯形时,应选择的图形是②。当这个四边形一定是平行四边形时,应选择的图形是①或③。
06
题型训练
例题精讲
02 平面图形的认识
3.一个长方形,其中三个角的顶点位置分别是(2,2)、(2,8)、(6,2)。
(1)请你在图中画出这个长方形。
(2)在上面画出的长方形中再画一个最大的圆,使所画的圆与这个长方形组成的组合图形只有1条对称轴。
【答案】
06
题型训练
例题精讲
03 平面图形的周长和面积
1.如图,小明将一个正方形纸剪出一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )。
A.16平方厘米 B.20平方厘米 C.80平方厘米 D.160平方厘米
【答案】C
【解答】解:设原正方形边长为x厘米。
5×(x-4)=4x
5x-20=4x
5x-4x-20=4x-4x
x-20=0
x-20+20=0+20
x=20
20×4=80(平方厘米)
一个长条面积为80平方厘米。
故答案为:C
06
题型训练
例题精讲
03 平面图形的周长和面积
2.有两张同样大小的长方形纸片,长10厘米,宽3厘米,把它们按图所示的方法叠合贴在一起,贴好后所成的“十”字图形,它的周长是 ,面积是 .
【答案】40厘米 51平方厘米
【解答】“十”字图形的周长为2个纸片,周长的和减去重叠部分正方形的周长,为(2×10+2×3)×2-4×3=40(厘米),“十”字图形的面积为2个纸片,面积的和减去重叠部分正方形的面积,为10×3×2-3×3=51(平方厘米)
06
题型训练
例题精讲
03 平面图形的周长和面积
3.如图,在一个梯形内有两个三角形的面积分别为10平方厘米和12平方厘米,已知梯形上、下底的比是2∶3,那么阴影部分的面积是多少平方厘米?
【答案】23平方厘米
【解答】假设上底为2厘米,下底为3厘米,
10×2÷2=10(厘米)
12×2÷3=8(厘米)
(2+3)×(10+8)÷2
=5×18÷2
=45(平方厘米)
45-10-12=23(平方厘米)
答:阴影部分面积是23平方厘米。
06
题型训练
例题精讲
04 立体图形的认识
1.礼品店要做一个长35厘米,宽25厘米,高15厘米的礼盒,用彩带按下图方法捆扎,接头处的彩带长20厘米。捆扎这个礼盒要用多少米长的彩带?(如图)
【答案】2米
【解答】35×2+25×2+15×4+20
=70+50+60+20
=120+60+20
=180+20
=200(厘米)
200厘米=2米
答:捆扎这个礼盒要用2米长的彩带。
06
题型训练
例题精讲
04 立体图形的认识
2.有一个正方体,每个面分别写上汉字:数、学、奥、林、匹、克。三个人从不同角度观察的结果如下图所示。这个正方体的每个汉字的对面各是什么字?
【答案】奥和克相对;林和学相对;数和匹相对
【解答】奥和克相对;
林和学相对;
数和匹相对;
答:奥和克相对;林和学相对;数和匹相对。
06
题型训练
例题精讲
05 立体图形的表面积和体积
1.长方体过同一顶点的三个面的面积分别是3、6、18,则这个长方体的体积是( )。
A.324 B.36 C.12 D.18
【答案】D
【解答】根据分析可知,长方体体积的平方=3×6×18
3×6×18=18×18
所以长方体体积为18。
故答案为:D
06
题型训练
例题精讲
05 立体图形的表面积和体积
2.求下面个圆柱的体积和表面积。(单位:cm)
【答案】体积56.52cm3;表面积99.81cm2
【解答】体积:3.14×32×8÷4
=226.08÷4
=56.52(立方厘米);
表面积:3.14×32÷2+3×8×2+3.14×3×2×8÷4
=14.13+48+37.68
=99.81(平方厘米)
07
专项训练
专项练习
1.工地上有一堆钢管,整体横截面是梯形,最上面一层有4根,最下面一层有8根,共堆放了5层,这堆钢管共有( )根。
2.一些棱长为4厘米的小正方体如图堆放在墙角处。
(1)这个物体露在外面的面有( )个。
(2)所有露在外面的面的面积是( )平方厘米。
30
17
272
07
专项训练
专项练习
3.如图,等边△ABC的边长是5,D,E分别是边AB,AC上的点,将△ADE沿直线DE折叠,点A落在处,且点在△ABC外部,则阴影图形的周长等于( ).
4.对于线段的中点,有以下几种说法:①若AM=MB,则M是AB的中点;②若AM=MB=AB,则M是AB的中点;③若AM=AB,则M是AB的中点;④若A,M,B在一条直线上,且AM=MB,则M是AB的中点.其中正确的是( ).
15
②④
07
专项训练
专项练习
5.一个圆柱和一个圆锥,它们的底面积相等,高的比是2:1,它们的体积比是( ).
6.时钟指示2点15分,它的时针和分针所成的锐角是多少度?( )。
A.45度 B.30度 C.25度50分 D.22度30分
6:1
D
07
专项训练
专项练习
7.从一张长为3厘米,宽为2厘米的长方形纸中剪去一个直径为1厘米的圆(如下图)。下面( )最接近阴影部分的面积。
A.5平方厘米 B.4平方厘米 C.3平方厘米 D.2平方厘米
8.在下面的硬纸中,能折成一个正方体的是( )。
A. B. C. D.
B
A
07
专项训练
专项练习
9.下面四个图形中,阴影部分面积最小的是( ).
A. B. C. D.
10.如图,工地上有一堆沙子,近似于圆锥形。沙堆的体积是6m3,高为1.5m,这个沙堆的占地面积是( )。
A.24m2 B.12m2 C.8m2 D.4m2
C
B
07
专项训练
专项练习
11.小东测量瓶子的容积(如下图),测得瓶子的底面直径是10厘米,然后给瓶子内盛入一些水,正放时水高15厘米,倒放时水高25厘米,瓶子深30厘米。这个瓶子的容积是多少毫升?(π取3.14)(单位:厘米)
3.14×(10÷2)2×15+3.14×(10÷2)2×(30-25)
=3.14×25×15+3.14×25×5
=3.14×25×(15+5)
=78.5×20
=1570(立方厘米)
1570立方厘米=1570毫升
答:这个瓶子的容积是1570毫升。
07
专项训练
专项练习
12.下面是一个国际标准田径跑道的示意图.跑道的一周是多少米?
73×3.14+85.39×2
=229.22 +170.78
=400(米)
答:跑道的一周是400米。
07
专项训练
专项练习
13.在一个等腰三角形中,有一个角是40°,求另外两个角的度数。
40°为顶角:
(180°-40°)÷2=70°
另外两个角的度数都是70°;
40°为一个底角:
180°-40°×2=100°
另外两个角的度数分别为40°、100°。
07
专项训练
专项练习
14.工人叔叔在粉刷教室,教室的长是9m,宽是8m,高是3.6m,门窗面积为21m ,要粉刷四周墙壁和顶棚.如果粉刷每平方米用环保漆300g,粉刷完这间教室共用环保漆多少千克?
9×8+9×3.6×2+8×3.6×2-21=173.4(m )
173.4×300=52020(g)=52.02(kg)
答:粉刷完这间教室共用环保漆52.02kg。
07
专项训练
专项练习
15.如图,ABCD是直角梯形,ACFE是长方形,已知BC-AD=4cm,CD=6cm,梯形面积是60cm2,求阴影部分的面积.
根据梯形的面积公式可知,(BC + AD)×CD÷2=60,所以BC + AD=20,又BC-AD=4,可求得BC=12(cm),AD=8(cm)
因为三角形ACD的面积=AC×CF÷2,而长方形ACFE的面积等于AC×CF,因此三角形ACD的面积等于阴影部分的面积,三角形ACD面积=AD×CD÷2=8×6÷2=24(cm2),因此阴影部分面积为24cm2.
答:阴影部分面积为24cm2。
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
