2024-2025学年北师大版七年级数学下册 1.1同底数幂的乘法 课件(共25张PPT)
文档属性
| 名称 | 2024-2025学年北师大版七年级数学下册 1.1同底数幂的乘法 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-25 17:25:42 | ||
图片预览








文档简介
(共25张PPT)
第一章 整式的乘除
第1课时 同底数幂的乘法
北师版七年级数学下册
1.1 幂的乘除
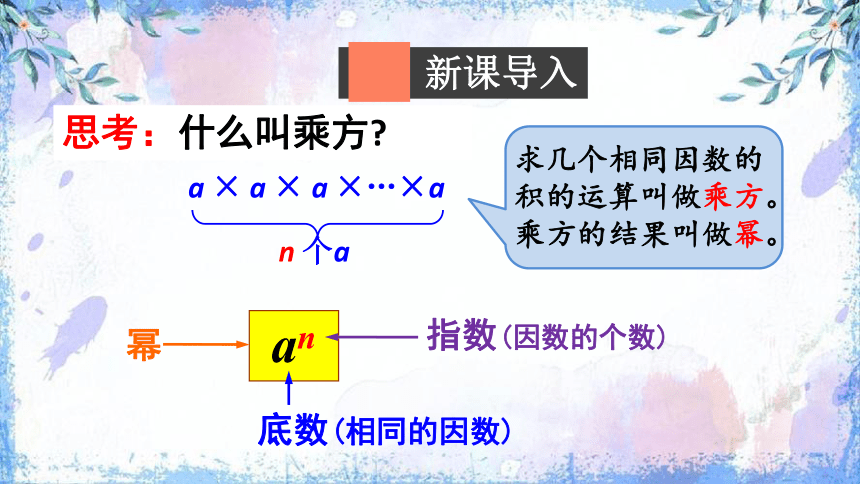
新课导入
思考:什么叫乘方
求几个相同因数的积的运算叫做乘方。乘方的结果叫做幂。
an
幂
底数(相同的因数)
指数(因数的个数)
a × a × a ×…×a
n 个a
填空
(1)25表示____________________;
(2) a的底数是______,指数是是______;
(3)(-2)4的底数是______,指数是是______;
(4)-24的底数是______,指数是是______。
2×2×2×2×2
a
1
-2
2
4
4
新课探究
光在真空中的传播速度约为3×108m/s,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年。
一年以 3×107 s 计算,比邻星与地球之间的距离大约是多少米
(1)怎样列式子
3×108×3×107×4.22
= 37.98×( 108×107 ) (m)
(2)观察这个算式,与以往的计算有何不同
108×107等于多少呢
同底数幂的乘法
1.计算下列各式:
(1)102×103;(2)105×108;
(3)10m×10n(m,n 都是正整数)。
尝试·思考
(1)102×103
(2)105×108
×(10×10×10)
= 105
= (10×10)
= (10×…×10)
5个10
× (10×…×10)
8个10
= (10×…×10)
13个10
= 1013
乘方的意义
乘方的意义
乘法的结合律
(3)10m×10n
= (10×…×10)
m个10
× (10×…×10)
n个10
= (10×…×10)
(m+n)个10
= 10m+n
乘方的意义
乘法的结合律
你发现了什么
底数为 10 的两个幂相乘,结果为底数仍为 10 的幂,它的指数为两个幂的指数的和。
2m×2n
2. 2m×2n 等于什么 和 (– 3)m×(– 3)n 呢
(m、n 都是正整数)
m 个 2
n 个 2
= (2×2×…×2)×(2×2×…×2)
= 2m+n
=()×()
m 个
n 个
= ()m+n
(– 3)m×(– 3) n
m 个 (– 3)
n 个 (– 3)
=[(–3)×(–3)×…×(–3)]× [(–3)×(–3)×…×(–3)]
= (–3) m+n
如果 m、n 都是正整数,那么 am·an 等于什么 为什么
am · an
尝试·交流
m 个 a
n 个 a
=( a · a · … · a )·( a · a · … · a)
= am+n。
通过刚才的计算,同学们是否能发现什么规律
同底数幂相乘,底数_____,指数_____。
不变
相加
am · an = am+n(m,n 都是正整数)
同底数幂的乘法法则:
运用法则的前提条件:
①底数相同;
②乘法运算。
两者缺一不可
例 1
(1)(– 3)7×(– 3)6;
(2) ;
(3)– x3 · x5;
(4)b2m · b2m+1。
解:(1) (– 3)7×(– 3)6 = (– 3)7+6 = (– 3)13;
(2) ;
(3)– x3 · x5 = – x3+5 = – x8 ;
(4)b2m · b2m+1 = b2m+2m+1 = b4m+1.
am · an · ap 等于什么 为什么
am · an · ap=(a·a· … ·a) · (a·a · … ·a)· (a·a · … ·a)
m 个 a
n 个 a
p 个 a
思考·交流
= am+n+p。
3个及以上的同底数幂相乘,底数不变,指数相加。
练习
(1)52 ×57 ; (2)7×73×72 ;
(3)– x2 · x5 ;(4)(– c)3 · (– c)m。
解:(1) 52 ×57 = 52+7 = 59;
(2)7×73×72 = 71+3+2 = 76 ;
(3) – x2 · x5 = – x2+5 = – x7 ;
(4)(– c)3 · (– c)m = (– c)3+m 。
1.计算:
【课本P3 随堂练习 第1题】
例 2 光在真空中的传播速度约为 3×108 m/s,太阳光照射到地球上大约需要 5×102 秒。地球距离太阳大约有多远
解: 3×108×5×102
= 15×1010
= 1.5×1011(m)。
因此,地球距离太阳大约有1.5×1011m。
2. 2017年6月,我国自主研发的“神威·太湖之光”
超级计算机以1.25×1017次/s 的峰值计算能力和 9.3×1016 次/s 的持续计算能力,第三次名列世界超级计算机排名榜单 TOP500 第一名。该超级计算机按持续计算能力运算 2×102 s可做多少次运算
解: 2×102×9.3×1016
= 18.6×(102×1016)
= 18.6×1018= 1.86×1019 (次)。
练习
【课本P3 随堂练习 第2题】
3.解决本课提出的比邻星与地球之间的距离问题。
解: 3×108×3×107×4.22
= 37.98×(108×107)
= 37.98×1015
= 3.798×1016 (m)。
练习
【课本P3 随堂练习 第3题】
随堂演练
1. 下列选项中,与 2n 为同底数幂的是( )
A.3n B. C.﹣2m D.(﹣2)m
2. 计算: ______。
C
3. 下面计算正确的是( )
A. (y – x)·(y – x)2·(y – x)3 = (x – y)6
B. (x – y)2·(y – x)3 = (x – y)5
C. (x – y)·(y – x)3·(x – y)2 = (x – y)6
D. (x – y)5·(y – x)2 = – (x – y)7
4. 计算: ______。
A
注意:不是同底数幂相乘时先化成同底数,再进行计算。
5. 已知xm=3,xn=5,求xm+n的值。
思路分析:
解:xm +n= xm · xn =3×5=15。
6. 如果 m,n 是正整数,且 3m·3n = 27,试求 mn 的值。
解:因为 3m·3n = 27 = 33,所以 m + n = 3.
又因为 m,n 是正整数,
所以当 m = 1 时,n = 2,此时 mn = 12 = 1;
当 m = 2 时,n = 1,此时 mn = 21 = 2。
课堂小结
同底数幂的乘法
am · an = am+n(m,n 都是正整数)
同底数幂相乘,底数不变,指数相加。
am · an·ap= am+n+p(m,n,p都是正整数)
法则
注意
底数相同时
直接应用法则
底数不相同时
先变成同底数再应用法则
课后作业
1.完成课本的相应练习题,
2.完成练习册本课时的习题。
第一章 整式的乘除
第1课时 同底数幂的乘法
北师版七年级数学下册
1.1 幂的乘除
新课导入
思考:什么叫乘方
求几个相同因数的积的运算叫做乘方。乘方的结果叫做幂。
an
幂
底数(相同的因数)
指数(因数的个数)
a × a × a ×…×a
n 个a
填空
(1)25表示____________________;
(2) a的底数是______,指数是是______;
(3)(-2)4的底数是______,指数是是______;
(4)-24的底数是______,指数是是______。
2×2×2×2×2
a
1
-2
2
4
4
新课探究
光在真空中的传播速度约为3×108m/s,太阳系以外距离地球最近的恒星是比邻星,它发出的光到达地球大约需要4.22年。
一年以 3×107 s 计算,比邻星与地球之间的距离大约是多少米
(1)怎样列式子
3×108×3×107×4.22
= 37.98×( 108×107 ) (m)
(2)观察这个算式,与以往的计算有何不同
108×107等于多少呢
同底数幂的乘法
1.计算下列各式:
(1)102×103;(2)105×108;
(3)10m×10n(m,n 都是正整数)。
尝试·思考
(1)102×103
(2)105×108
×(10×10×10)
= 105
= (10×10)
= (10×…×10)
5个10
× (10×…×10)
8个10
= (10×…×10)
13个10
= 1013
乘方的意义
乘方的意义
乘法的结合律
(3)10m×10n
= (10×…×10)
m个10
× (10×…×10)
n个10
= (10×…×10)
(m+n)个10
= 10m+n
乘方的意义
乘法的结合律
你发现了什么
底数为 10 的两个幂相乘,结果为底数仍为 10 的幂,它的指数为两个幂的指数的和。
2m×2n
2. 2m×2n 等于什么 和 (– 3)m×(– 3)n 呢
(m、n 都是正整数)
m 个 2
n 个 2
= (2×2×…×2)×(2×2×…×2)
= 2m+n
=()×()
m 个
n 个
= ()m+n
(– 3)m×(– 3) n
m 个 (– 3)
n 个 (– 3)
=[(–3)×(–3)×…×(–3)]× [(–3)×(–3)×…×(–3)]
= (–3) m+n
如果 m、n 都是正整数,那么 am·an 等于什么 为什么
am · an
尝试·交流
m 个 a
n 个 a
=( a · a · … · a )·( a · a · … · a)
= am+n。
通过刚才的计算,同学们是否能发现什么规律
同底数幂相乘,底数_____,指数_____。
不变
相加
am · an = am+n(m,n 都是正整数)
同底数幂的乘法法则:
运用法则的前提条件:
①底数相同;
②乘法运算。
两者缺一不可
例 1
(1)(– 3)7×(– 3)6;
(2) ;
(3)– x3 · x5;
(4)b2m · b2m+1。
解:(1) (– 3)7×(– 3)6 = (– 3)7+6 = (– 3)13;
(2) ;
(3)– x3 · x5 = – x3+5 = – x8 ;
(4)b2m · b2m+1 = b2m+2m+1 = b4m+1.
am · an · ap 等于什么 为什么
am · an · ap=(a·a· … ·a) · (a·a · … ·a)· (a·a · … ·a)
m 个 a
n 个 a
p 个 a
思考·交流
= am+n+p。
3个及以上的同底数幂相乘,底数不变,指数相加。
练习
(1)52 ×57 ; (2)7×73×72 ;
(3)– x2 · x5 ;(4)(– c)3 · (– c)m。
解:(1) 52 ×57 = 52+7 = 59;
(2)7×73×72 = 71+3+2 = 76 ;
(3) – x2 · x5 = – x2+5 = – x7 ;
(4)(– c)3 · (– c)m = (– c)3+m 。
1.计算:
【课本P3 随堂练习 第1题】
例 2 光在真空中的传播速度约为 3×108 m/s,太阳光照射到地球上大约需要 5×102 秒。地球距离太阳大约有多远
解: 3×108×5×102
= 15×1010
= 1.5×1011(m)。
因此,地球距离太阳大约有1.5×1011m。
2. 2017年6月,我国自主研发的“神威·太湖之光”
超级计算机以1.25×1017次/s 的峰值计算能力和 9.3×1016 次/s 的持续计算能力,第三次名列世界超级计算机排名榜单 TOP500 第一名。该超级计算机按持续计算能力运算 2×102 s可做多少次运算
解: 2×102×9.3×1016
= 18.6×(102×1016)
= 18.6×1018= 1.86×1019 (次)。
练习
【课本P3 随堂练习 第2题】
3.解决本课提出的比邻星与地球之间的距离问题。
解: 3×108×3×107×4.22
= 37.98×(108×107)
= 37.98×1015
= 3.798×1016 (m)。
练习
【课本P3 随堂练习 第3题】
随堂演练
1. 下列选项中,与 2n 为同底数幂的是( )
A.3n B. C.﹣2m D.(﹣2)m
2. 计算: ______。
C
3. 下面计算正确的是( )
A. (y – x)·(y – x)2·(y – x)3 = (x – y)6
B. (x – y)2·(y – x)3 = (x – y)5
C. (x – y)·(y – x)3·(x – y)2 = (x – y)6
D. (x – y)5·(y – x)2 = – (x – y)7
4. 计算: ______。
A
注意:不是同底数幂相乘时先化成同底数,再进行计算。
5. 已知xm=3,xn=5,求xm+n的值。
思路分析:
解:xm +n= xm · xn =3×5=15。
6. 如果 m,n 是正整数,且 3m·3n = 27,试求 mn 的值。
解:因为 3m·3n = 27 = 33,所以 m + n = 3.
又因为 m,n 是正整数,
所以当 m = 1 时,n = 2,此时 mn = 12 = 1;
当 m = 2 时,n = 1,此时 mn = 21 = 2。
课堂小结
同底数幂的乘法
am · an = am+n(m,n 都是正整数)
同底数幂相乘,底数不变,指数相加。
am · an·ap= am+n+p(m,n,p都是正整数)
法则
注意
底数相同时
直接应用法则
底数不相同时
先变成同底数再应用法则
课后作业
1.完成课本的相应练习题,
2.完成练习册本课时的习题。
同课章节目录
