华师大版七下(2024版)9.2.1图形的平移教案
文档属性
| 名称 | 华师大版七下(2024版)9.2.1图形的平移教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 14:15:45 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
分课时教学设计
《9.2.1图形的平称》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本课为华师大版七年级下册第九章《图形的平移》第一课时,严格聚焦 "平移概念的建构与初步应用",是后续学习平移特征(第二课时)的逻辑起点。教材通过生活实例抽象(滑雪、电梯、火车行驶)和数学操作具象化(三角板平移画平行线),引导学生理解平移的本质——在平面内,图形沿固定方向等距移动,形状大小不变。核心任务是建立 "方向" 与 "距离" 的双要素认知,识别平移中的对应点、对应线段、对应角,避免涉及平移性质(如线段平行相等)和作图方法(如关键点定位)的深度探究。
学习者分析 学生已掌握轴对称概念,理解 "图形变换中形状大小不变" 的特性;能识别教材中典型平移现象,但对 "斜向平移"" 多对应点关系 " 缺乏精确认知。可能将 "移动方向" 等同于 "物体朝向",或忽略 "各点移动距离相等" 的本质;习惯用生活语言描述平移,难以用数学语言精准表达。
教学目标 1.能结合教材实例说出平移的定义,明确平移由方向和距离决定; 2.能在简单图形平移中,准确找出对应点、对应线段、对应角,理解 "图形各点同步平移" 的特性。 3.通过 "观察生活实例→归纳共同特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象能力。 4.发现平移在现实中的应用,体会数学对物体运动的精准描述作用,增强 "用数学眼光分析生活现象" 的意识。
教学重点 1.理解平移的概念和双要素:方向和距离. 2.对正确识别平移前后图形的对应点,对应线段,对应角,理解 "平移后图形各元素一一对应" 的特性.
教学难点 排除 "物体运动速度"" 运动轨迹曲直 "等非本质因素干扰,抓住" 沿固定方向等距移动 " 的核心特征,区分平移与其他运动.
学习活动设计
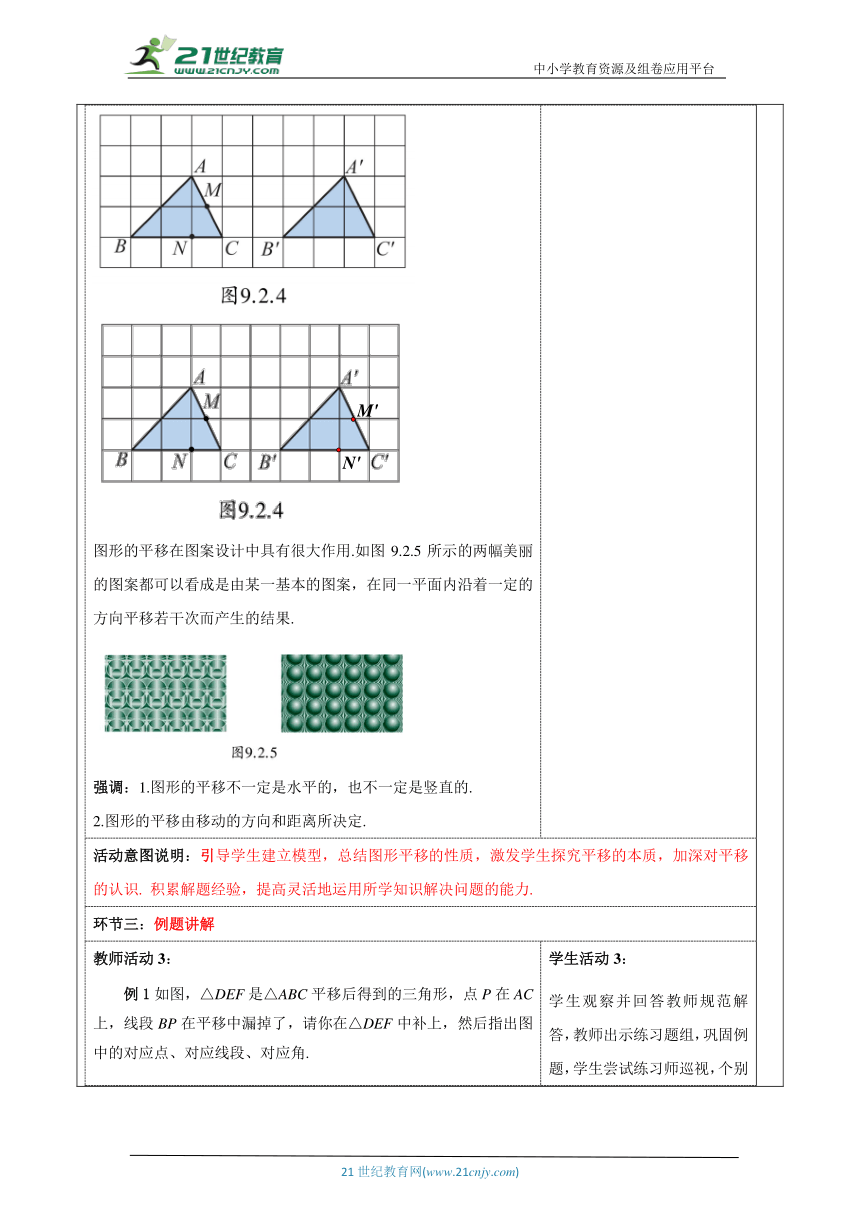
教师活动学生活动环节一:情境导入教师活动1: 在日常生活中,我们经常可以看到如图 9.2.1 所示的一些现象: 滑雪运动员在白茫茫的平坦雪地上滑行, 大楼电梯上上下下地迎送来客, 火车在笔直的铁轨上飞驰而过, 飞机起飞前在跑道上加速滑行, 这些都给我们以物体平行移动的感觉. 注:本章主要研究平面图形在一个平面上的平移问题.学生活动1: 学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.活动意图说明: 从实际出发,从学生已有的生活经验出发,通过具体实例认识图形的平移.环节二:新知探究教师活动2: 思考:上面这些现象都给我们以物体平行移动的感觉.你能说说它们有什么样的共同特征吗? 上述现象中的物体只发生了位置的变化,形状、大小均未改变. 总结归纳:如图9.2.2,在同一平面内,三角板沿着由点A到点B的方向,从M处平行移动到N处. 像这样的运动叫做平移.平移由移动的方向和距离决定. 如图9.2.3,当我们使用直尺与三角板画平行线时,△ABC沿着直尺PQ平移到△A'B'C'的位置,就可以画出 AB的平行线A'B'了. 我们把点A与点A'叫做对应点,线段AB与线段A′B′叫做对应线段,∠A与∠A'叫做对应角. 填空: 点B的对应点是点 B' ;点C的对应点是点 C' ;线段AC的对应线段是线段 A'C' ;线段BC的对应线段是线段 B'C' ;∠B的对应角是 ∠B' ;∠C的对应角是 ∠C' . △ABC平移的方向就是由点B到点 B' 的方向,平移的距离就是线段BB'的 长度 . 试一试:在图9.2.4中,△ABC沿着由点A到点A′的方向,平移到△A'B'C'的位置.你知道线段AC的中点M以及线段BC上的点N平移到什么地方去了吗?请在图上标出它们的对应点M'和N'的位置. 图形的平移在图案设计中具有很大作用.如图9.2.5所示的两幅美丽的图案都可以看成是由某一基本的图案,在同一平面内沿着一定的方向平移若干次而产生的结果. 强调:1.图形的平移不一定是水平的,也不一定是竖直的. 2.图形的平移由移动的方向和距离所决定.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,总结图形平移的性质,激发学生探究平移的本质,加深对平移的认识. 积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1如图,△DEF是△ABC平移后得到的三角形,点P在AC上,线段BP在平移中漏掉了,请你在△DEF中补上,然后指出图中的对应点、对应线段、对应角. 【答案】如图,EG为BP平移后的对应线段. 对应点:点A与点D,点B与点E,点C与点F,点P与点G. 对应线段:AB与DE,BC与EF,AC与DF,BP与EG. 对应角:∠A与∠D,∠ABC与∠DEF,∠C与∠F. 【总结】本题考查了利用平移变换作图,熟记平移变换的性质是解题的关键. 例2 如图,△ABC是△DEF经过平移得到的,若,则BE= ,,若为的中点,为的中点,则. 【答案】4 cm,4 cm,4 cm 【总结】图形在平移的过程中对应点间的距离就是平移的距离. 总结:平移的基本特征:图形的大小、形状都不改变,只改变图形的位置. 平移的对应元素:对应顶点、对应边(线段)、对应角.学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 认识图形的平移变换,理解平移的概念及平移的决定条件.活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过生活中实例认识图形的平移变换,探索它的基本性质.能按要求画出简单的平面图形平移后的图形,培养学生观察问题、分析问题、解决问题的能力.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.2 平 移 9.2.1 图形的平移 平移的概念: 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.下列图形中,不能通过其中一个四边形平移得到的是( ) 2.小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形的顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( ) A.3种 B.4种 C.5种 D.无数种 3.如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将△ABC平移到△DEF的位置,下面的平移步骤正确的是( ) A.把△ABC先向左平移5个单位长度,再向下平移2个单位长度 B.把△ABC先向右平移5个单位长度,再向下平移2个单位长度 C.把△ABC先向左平移5个单位长度,再向上平移2个单位长度 D.把△ABC先向右平移5个单位长度,再向上平移2个单位长度 选做题: 4.如图,△EFD是由△ABC平移得到的,则平移的距离为( ) A.线段AB的长度 B.线段AE的长度 C.线段BE的长度 D.线段EF的长度 5.如图,△DEF是由△ABC平移得到的,则平移的方向是____________,平移的距离是____________. 6.如图,把三角尺的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC′=________. 【综合拓展类作业】 7.平移变换不仅与几何图形有着密切的联系,而且在一些特殊结构的汉字中,也有平移变换的现象,如:“日”“朋”“圭”等,请你开动脑筋,再写出两个具有平移变换现象的汉字:________. 8.新定义问题在如图的方格纸中,把一个图形先沿水平方向平移|a|个格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|个格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为[a,b].例如:把图中的△ABC先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为[3,-5].若再将△A1B1C1经过[5,2]得到△A2B2C2,则△ABC经过平移得到△A2B2C2的过程是( ) A.[2,7] B.[8,-3] C.[8,-7] D.[-8,-2]
1.[答案] D 2.[解析] C ①正方形向上平移;②正方形向下平移;③正方形向右平移;④将正方形沿射线BD的方向平移;⑤将正方形沿射线AC的方向平移.故有5种平移方向. 3.[解析] A 注意是从△ABC平移到△DEF,只需观察点A是如何平移到点D的位置,即可判断平移的方向和距离. 4.[解析] B 点A,E为对应点,故线段AE的长度可作为平移的距离. 5.[答案] 答案不唯一,如:点A到点D的方向 线段AD的长度 6.[答案] 5 cm 7.[答案] 答案不唯一,如弱、喆 8 [解析] B ∵两次平移后△ABC水平方向的变化分别为3,5,说明图形先向右平移了3格后,又向右平移了5格,那么一共向右平移了3+5=8(格); 竖直方向的变化分别为-5,2,说明图形先向下平移了5格后,又向上平移了2格,那么竖直方向平移了-5+2=-3(格), ∴△ABC经过平移得到△A2B2C2的过程是[8,-3]. 故选B.
作业设计 【知识技能类作业】 必做题: 1.如图,若△DEF是由△ABC平移后得到的,已知点A、D之间的距离为1,CE=2,则BC的长为( ) 第1题图 A.3 B.1 C.2 D.不确定 2.如图,在△ABC中,∠C=90°,AC=4,将△ABC沿CB方向平移得到△DEF.若四边形ABED的面积等于8,则平移的距离为 . 第2题图 3.如图,已知△DEF是由△ABC平移所得. (1)点A的对应点是点 ,点B的对应点是点 ,点C的对应点是点 ; (2)对应角∠ABC= ,∠BAC= ,∠ACB= ; (3)线段AD、BE、CF叫做对应点间的连线,猜想这三条线段之间有什么关系呢?(无需证明) 选做题: 4.如图,网格中的每个小正方形的边长都是1个单位长度,图中“鱼”的各个顶点都在格点上.把“鱼”先向右平移5个单位长度,再向下平移1个单位长度,画出平移后的图形,并求出平移后的“鱼”的面积. 5.如图,将△ABC沿着从B到D的方向平移后得到△EDF.若AE=12cm,CE=4cm. (1)△ABC平移的距离是多少? (2)求线段BD、EF的长. 【综合拓展类作业】 6.南湖公园有很多长方形草地,草地里修了很多有趣的小路.如图,三个图形都是长为50m、宽为30m的长方形草地,且小路的宽都是1m. (1)如图1,阴影部分为1m宽的小路(FF1=EE1=1m),长方形除去阴影部分后剩余部分为草地,则草地的面积为 ; 图1 (2)如图2,有两条宽均为1m的小路(图中阴影部分),则草地的面积为 ; 图2 (3)如图3,非阴影部分为1m宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 . 图3 答案:1.A 2.2 3.(1)D E F (2)∠DEF ∠EDF ∠DFE (3)AD∥BE∥CF,AD=BE=CF. 4.作图略,平移后的“鱼”的面积为11. 5.(1)平移的距离是12cm. (2)BD=12cm,EF=8cm. 6.(1)1470m2 (2)1421m2 (3)108m
教学反思 本节课通过实例认识图形的平移,发现和识别生活中的平移现象,经过作图的操作过程,能按要求作出简单平面图形平移后的图形,并能指出平移前后的点、线段与角的对应关系,提高作图能力,发展空间观念,进一步增强数学应用意识及审美意识,培养学生对图形的欣赏意识.
21世纪教育网(www.21cnjy.com)
分课时教学设计
《9.2.1图形的平称》教学设计
课型 新授课 复习课 试卷讲评课 其他课
教学内容分析 本课为华师大版七年级下册第九章《图形的平移》第一课时,严格聚焦 "平移概念的建构与初步应用",是后续学习平移特征(第二课时)的逻辑起点。教材通过生活实例抽象(滑雪、电梯、火车行驶)和数学操作具象化(三角板平移画平行线),引导学生理解平移的本质——在平面内,图形沿固定方向等距移动,形状大小不变。核心任务是建立 "方向" 与 "距离" 的双要素认知,识别平移中的对应点、对应线段、对应角,避免涉及平移性质(如线段平行相等)和作图方法(如关键点定位)的深度探究。
学习者分析 学生已掌握轴对称概念,理解 "图形变换中形状大小不变" 的特性;能识别教材中典型平移现象,但对 "斜向平移"" 多对应点关系 " 缺乏精确认知。可能将 "移动方向" 等同于 "物体朝向",或忽略 "各点移动距离相等" 的本质;习惯用生活语言描述平移,难以用数学语言精准表达。
教学目标 1.能结合教材实例说出平移的定义,明确平移由方向和距离决定; 2.能在简单图形平移中,准确找出对应点、对应线段、对应角,理解 "图形各点同步平移" 的特性。 3.通过 "观察生活实例→归纳共同特征→抽象数学概念" 的探究过程,经历从具体到抽象的概念建构,发展数学抽象能力。 4.发现平移在现实中的应用,体会数学对物体运动的精准描述作用,增强 "用数学眼光分析生活现象" 的意识。
教学重点 1.理解平移的概念和双要素:方向和距离. 2.对正确识别平移前后图形的对应点,对应线段,对应角,理解 "平移后图形各元素一一对应" 的特性.
教学难点 排除 "物体运动速度"" 运动轨迹曲直 "等非本质因素干扰,抓住" 沿固定方向等距移动 " 的核心特征,区分平移与其他运动.
学习活动设计
教师活动学生活动环节一:情境导入教师活动1: 在日常生活中,我们经常可以看到如图 9.2.1 所示的一些现象: 滑雪运动员在白茫茫的平坦雪地上滑行, 大楼电梯上上下下地迎送来客, 火车在笔直的铁轨上飞驰而过, 飞机起飞前在跑道上加速滑行, 这些都给我们以物体平行移动的感觉. 注:本章主要研究平面图形在一个平面上的平移问题.学生活动1: 学生通过已学习的知识经过个人思考、小组合作等方式推导出本课新知.活动意图说明: 从实际出发,从学生已有的生活经验出发,通过具体实例认识图形的平移.环节二:新知探究教师活动2: 思考:上面这些现象都给我们以物体平行移动的感觉.你能说说它们有什么样的共同特征吗? 上述现象中的物体只发生了位置的变化,形状、大小均未改变. 总结归纳:如图9.2.2,在同一平面内,三角板沿着由点A到点B的方向,从M处平行移动到N处. 像这样的运动叫做平移.平移由移动的方向和距离决定. 如图9.2.3,当我们使用直尺与三角板画平行线时,△ABC沿着直尺PQ平移到△A'B'C'的位置,就可以画出 AB的平行线A'B'了. 我们把点A与点A'叫做对应点,线段AB与线段A′B′叫做对应线段,∠A与∠A'叫做对应角. 填空: 点B的对应点是点 B' ;点C的对应点是点 C' ;线段AC的对应线段是线段 A'C' ;线段BC的对应线段是线段 B'C' ;∠B的对应角是 ∠B' ;∠C的对应角是 ∠C' . △ABC平移的方向就是由点B到点 B' 的方向,平移的距离就是线段BB'的 长度 . 试一试:在图9.2.4中,△ABC沿着由点A到点A′的方向,平移到△A'B'C'的位置.你知道线段AC的中点M以及线段BC上的点N平移到什么地方去了吗?请在图上标出它们的对应点M'和N'的位置. 图形的平移在图案设计中具有很大作用.如图9.2.5所示的两幅美丽的图案都可以看成是由某一基本的图案,在同一平面内沿着一定的方向平移若干次而产生的结果. 强调:1.图形的平移不一定是水平的,也不一定是竖直的. 2.图形的平移由移动的方向和距离所决定.学生活动2: 学生小组合作交流. 学生可小组合作交流,自主探究,得出结论 教师巡视,听取学生的看法、见解,随时参与讨论. 活动意图说明:引导学生建立模型,总结图形平移的性质,激发学生探究平移的本质,加深对平移的认识. 积累解题经验,提高灵活地运用所学知识解决问题的能力.环节三:例题讲解教师活动3: 例1如图,△DEF是△ABC平移后得到的三角形,点P在AC上,线段BP在平移中漏掉了,请你在△DEF中补上,然后指出图中的对应点、对应线段、对应角. 【答案】如图,EG为BP平移后的对应线段. 对应点:点A与点D,点B与点E,点C与点F,点P与点G. 对应线段:AB与DE,BC与EF,AC与DF,BP与EG. 对应角:∠A与∠D,∠ABC与∠DEF,∠C与∠F. 【总结】本题考查了利用平移变换作图,熟记平移变换的性质是解题的关键. 例2 如图,△ABC是△DEF经过平移得到的,若,则BE= ,,若为的中点,为的中点,则. 【答案】4 cm,4 cm,4 cm 【总结】图形在平移的过程中对应点间的距离就是平移的距离. 总结:平移的基本特征:图形的大小、形状都不改变,只改变图形的位置. 平移的对应元素:对应顶点、对应边(线段)、对应角.学生活动3: 学生观察并回答教师规范解答,教师出示练习题组,巩固例题,学生尝试练习师巡视,个别指导. 认识图形的平移变换,理解平移的概念及平移的决定条件.活动意图说明: 让学生在一定的数学活动中去体验、感受数学,通过生活中实例认识图形的平移变换,探索它的基本性质.能按要求画出简单的平面图形平移后的图形,培养学生观察问题、分析问题、解决问题的能力.从而更好地理解知识,让学生的认知结构得到不断的完善.
板书设计 9.2 平 移 9.2.1 图形的平移 平移的概念: 例1 例2
课堂练习 【知识技能类作业】 必做题: 1.下列图形中,不能通过其中一个四边形平移得到的是( ) 2.小军同学在网格纸上将某些图形进行平移操作,他发现平移前后的两个图形所组成的图形可以是轴对称图形.如图所示,现在他将正方形ABCD从当前位置开始进行一次平移操作,平移后的正方形的顶点也在格点上,则使平移前后的两个正方形组成轴对称图形的平移方向有( ) A.3种 B.4种 C.5种 D.无数种 3.如图,在10×6的网格中,每个小方格的边长都是1个单位长度,将△ABC平移到△DEF的位置,下面的平移步骤正确的是( ) A.把△ABC先向左平移5个单位长度,再向下平移2个单位长度 B.把△ABC先向右平移5个单位长度,再向下平移2个单位长度 C.把△ABC先向左平移5个单位长度,再向上平移2个单位长度 D.把△ABC先向右平移5个单位长度,再向上平移2个单位长度 选做题: 4.如图,△EFD是由△ABC平移得到的,则平移的距离为( ) A.线段AB的长度 B.线段AE的长度 C.线段BE的长度 D.线段EF的长度 5.如图,△DEF是由△ABC平移得到的,则平移的方向是____________,平移的距离是____________. 6.如图,把三角尺的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC′=________. 【综合拓展类作业】 7.平移变换不仅与几何图形有着密切的联系,而且在一些特殊结构的汉字中,也有平移变换的现象,如:“日”“朋”“圭”等,请你开动脑筋,再写出两个具有平移变换现象的汉字:________. 8.新定义问题在如图的方格纸中,把一个图形先沿水平方向平移|a|个格(当a为正数时,表示向右平移;当a为负数时,表示向左平移),再沿竖直方向平移|b|个格(当b为正数时,表示向上平移;当b为负数时,表示向下平移),得到一个新的图形,我们把这个过程记为[a,b].例如:把图中的△ABC先向右平移3格,再向下平移5格得到△A1B1C1,可以把这个过程记为[3,-5].若再将△A1B1C1经过[5,2]得到△A2B2C2,则△ABC经过平移得到△A2B2C2的过程是( ) A.[2,7] B.[8,-3] C.[8,-7] D.[-8,-2]
1.[答案] D 2.[解析] C ①正方形向上平移;②正方形向下平移;③正方形向右平移;④将正方形沿射线BD的方向平移;⑤将正方形沿射线AC的方向平移.故有5种平移方向. 3.[解析] A 注意是从△ABC平移到△DEF,只需观察点A是如何平移到点D的位置,即可判断平移的方向和距离. 4.[解析] B 点A,E为对应点,故线段AE的长度可作为平移的距离. 5.[答案] 答案不唯一,如:点A到点D的方向 线段AD的长度 6.[答案] 5 cm 7.[答案] 答案不唯一,如弱、喆 8 [解析] B ∵两次平移后△ABC水平方向的变化分别为3,5,说明图形先向右平移了3格后,又向右平移了5格,那么一共向右平移了3+5=8(格); 竖直方向的变化分别为-5,2,说明图形先向下平移了5格后,又向上平移了2格,那么竖直方向平移了-5+2=-3(格), ∴△ABC经过平移得到△A2B2C2的过程是[8,-3]. 故选B.
作业设计 【知识技能类作业】 必做题: 1.如图,若△DEF是由△ABC平移后得到的,已知点A、D之间的距离为1,CE=2,则BC的长为( ) 第1题图 A.3 B.1 C.2 D.不确定 2.如图,在△ABC中,∠C=90°,AC=4,将△ABC沿CB方向平移得到△DEF.若四边形ABED的面积等于8,则平移的距离为 . 第2题图 3.如图,已知△DEF是由△ABC平移所得. (1)点A的对应点是点 ,点B的对应点是点 ,点C的对应点是点 ; (2)对应角∠ABC= ,∠BAC= ,∠ACB= ; (3)线段AD、BE、CF叫做对应点间的连线,猜想这三条线段之间有什么关系呢?(无需证明) 选做题: 4.如图,网格中的每个小正方形的边长都是1个单位长度,图中“鱼”的各个顶点都在格点上.把“鱼”先向右平移5个单位长度,再向下平移1个单位长度,画出平移后的图形,并求出平移后的“鱼”的面积. 5.如图,将△ABC沿着从B到D的方向平移后得到△EDF.若AE=12cm,CE=4cm. (1)△ABC平移的距离是多少? (2)求线段BD、EF的长. 【综合拓展类作业】 6.南湖公园有很多长方形草地,草地里修了很多有趣的小路.如图,三个图形都是长为50m、宽为30m的长方形草地,且小路的宽都是1m. (1)如图1,阴影部分为1m宽的小路(FF1=EE1=1m),长方形除去阴影部分后剩余部分为草地,则草地的面积为 ; 图1 (2)如图2,有两条宽均为1m的小路(图中阴影部分),则草地的面积为 ; 图2 (3)如图3,非阴影部分为1m宽的小路,沿着小路的中间从入口E处走到出口F处,所走的路线(图中虚线)长为 . 图3 答案:1.A 2.2 3.(1)D E F (2)∠DEF ∠EDF ∠DFE (3)AD∥BE∥CF,AD=BE=CF. 4.作图略,平移后的“鱼”的面积为11. 5.(1)平移的距离是12cm. (2)BD=12cm,EF=8cm. 6.(1)1470m2 (2)1421m2 (3)108m
教学反思 本节课通过实例认识图形的平移,发现和识别生活中的平移现象,经过作图的操作过程,能按要求作出简单平面图形平移后的图形,并能指出平移前后的点、线段与角的对应关系,提高作图能力,发展空间观念,进一步增强数学应用意识及审美意识,培养学生对图形的欣赏意识.
21世纪教育网(www.21cnjy.com)
