华师大版七下(2024版)9.2.2平移的特征 课件
文档属性
| 名称 | 华师大版七下(2024版)9.2.2平移的特征 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-20 00:00:00 | ||
图片预览







文档简介
第九章 轴对称、平移与旋转
9.2.2平移的特征
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能结合教材实例准确描述平移的特征; 能应用平移特征完成平移作图任务;
01
通过 "操作观察→数据测量→归纳验证" 的探究过程,经历从具体到抽象的数学建模,发展推理意识与几何直观;
02
发现平移特征在建筑设计、工业制造中的应用,体会数学对现实问题的解释力,增强应用意识.
03
02
复习导入
1.平移的定义: .
2.平移的两要素是 和 。
回顾旧知:
将一个图形沿着某个方向移动一定的距离的图形运动
方向
距离
你会用三角板、直尺画平行线吗?如果直尺是倾斜的,用三角板是否还能画出平行线?
03
新知探究
探究一
平移的特征
如图9.2.6, 在画平行线的时候, 有时为了需要, 将直尺和三角板放在倾斜的位置上. 但不管怎样, 我们总可以推得 A′B′∥AB, A′B′=AB, ∠B′=∠B.
同时也有A′C′∥ , A′C′ = , ∠C′ = .
B′C′与BC , B′C′ = , ∠A′ = .
A′C′
A′C′
∠C
平行
BC
∠A
你有什么发现?
03
新知探究
图形平移的特征:
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等, 对应角相等, 图形的形状和大小不变.
概括
(1)连结对应点的线段的长度就是平移距离(上述中的BB′);
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向;
(3)平移前后图形的对应边平行且相等,对应角相等.
注意
03
新知探究
观察图9.2.7, △ABC沿着PQ方向平移到△A′B′C′的位置, 我们可以看到, △ABC上的每一点都作了相同的平移: A→A′, B→B′, C→C′.
你发现对应点所连的线段有什么特点了吗?
不难发现:
AA′∥BB′, AA′=BB′;
AA′∥ , AA′= ;
BB′与CC′ , BB′= .
BB′
BB′
平行
CC′
由此我们还可以得到:
平移后对应点所连的线段平行(或在同一条直线上)且相等.
概括
02
新知探究
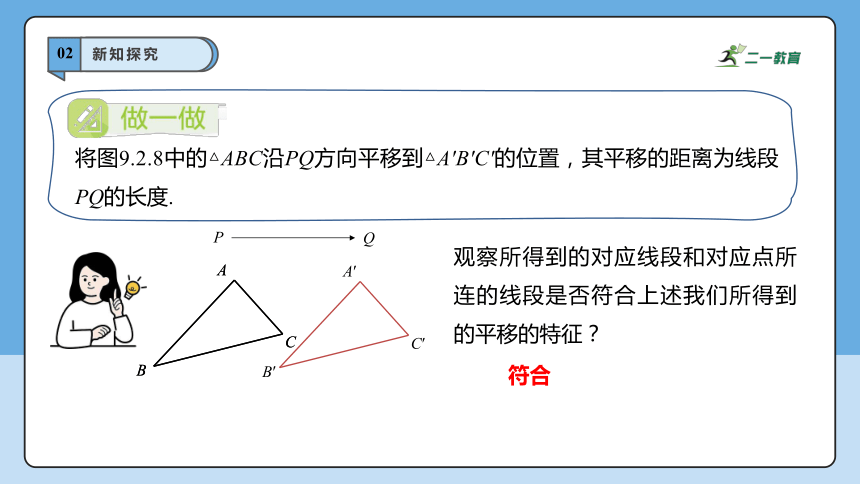
将图9.2.8中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
A
C
B
Q
P
A′
C′
B′
A
C
B
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得到的平移的特征?
符合
03
例题讲解
解析:由于点A与点A′是一对对应点, 因此, 如图9.2.9②, 连结AA′,平移的方向就是点A到点A′的方向,平移的距离就是线段 AA′的长, 经测量可知,约25 mm .
如图9.2.9①所示,△ABC经过平移后到△A'B'C'的位置.指出平移的方向,并量出平移的距离. (精确到1mm)
例1
【总结】平移的距离就是一对对应点连线的长度.
03
新知探究
探究二
平移作图
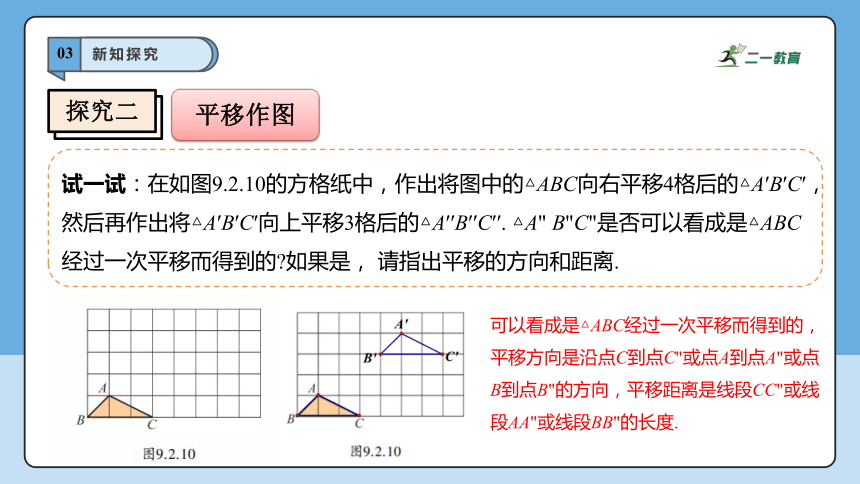
试一试:在如图9.2.10的方格纸中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′向上平移3格后的△A′′B′′C′′. △A" B"C"是否可以看成是△ABC经过一次平移而得到的?如果是, 请指出平移的方向和距离.
可以看成是△ABC经过一次平移而得到的,平移方向是沿点C到点C"或点A到点A"或点B到点B"的方向,平移距离是线段CC"或线段AA"或线段BB"的长度.
03
新知讲解
平移作图的一般步骤:平移作图是平移基本性质的应用,利用平移可以得到许多美丽的图案,在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连结点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连结对应点.
02
新知探究
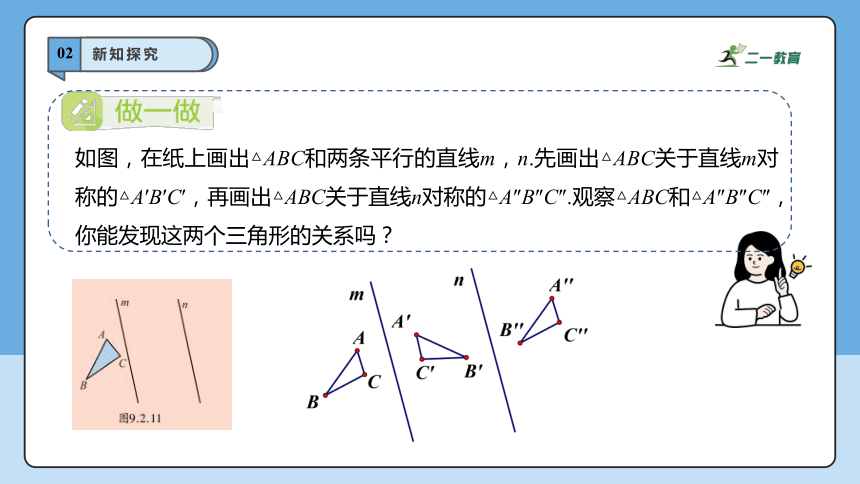
如图,在纸上画出△ABC和两条平行的直线m,n.先画出△ABC关于直线m对称的△A′B′C′,再画出△ABC关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形的关系吗?
03
新知讲解
【总结】经过两次翻折(对称轴互相平行)后得到的图形,可以看成是原图形经过平移得到的,即两次翻折相当于一次平移.
03
例题讲解
如图,在8×8的正方形网格中,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC先向右平移4个单位,再向上平移3个单位得△A1B1C1.
(1)作出平移后的△A1B1C1;
(2)求△A1B1C的面积.
例2
分析
(1)图形经过了几次平移?怎样作出多次平移后的图形?
(2)可直接求出△A1B1C的面积吗?△A1B1C的面积能转换成哪些图形面积的和(差)?
03
例题讲解
解析
(1)如图所示,△A1B1C1即为所求.
(2)由图可知,△A1B1C的面积为12×3×6?12×2×2?12×1×4?1×2=3.
?
03
新知讲解
【总结】此题主要考查了平移变换以及三角形面积求法等知识,根据题意正确把握平移的性质是解题关键.
作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连结对应点即可得到平移后的图形.
1.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N.下列各角可以由∠END通过平移得到的角是( )
A.∠CNF B.∠AMF C.∠EMB D.∠AME
04
课堂练习
【知识技能类作业】必做题:
C
2.如图,将三角形ABC沿着PQ方向平移得到三角形A'B'C',则下列结论错误的是( )?
A.AB∥A'B' B.AA'=BB' C.AA'∥BB' D.AA'=AB
D
04
课堂练习
【知识技能类作业】必做题:
3.如图,平移方格纸中的图形,使点A平移到点A'处,画出平移后的图形.
解:如图所示
4.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
04
课堂练习
【知识技能类作业】选做题:
A
5.如图,一把直尺沿直线断开并发生平移,点E,D,B,F在同一条直线上,若∠DBC=62°,则∠ADE的度数为( )?
A.62° B.118° C.128° D.130°
B
6.如图,△ABC沿着BC方向平移得到△A'B'C',点P是直线AA'上任意一点,若△ABC,△PB'C'的面积分别为S1,S2,则下列关系正确的是( )
?
A.S1>S2 B.S104
课堂练习
【知识技能类作业】选做题:
C
04
课堂练习
【知识技能类作业】选做题:
解:(1)∵边AB沿着AC方向平移到ED,
∴AC∥DB,∴∠C=∠CBD=60°,
∵∠AEB=∠C+∠EBC,
∴∠EBC=70°-60°=10°;
(2)∵AB=ED,AE=DB,
∴△EOC与△BOD周长的和为CE+CO+EO+OD+OB+DB=DE+BC+EC+AE=AB+BC+AC=7+8+3=18.
7.如图,将△ABC中的边AB沿着AC方向平移到ED,ED交BC于点O,连结BD,BE.
(1)若∠AEB=70°,∠CBD=60°,求∠EBC的大小;
(2)若AB=7,BC=8,AC=3,边AB在平移的过程中,点E始终在边AC上(不与点A,点C重合),求△EOC与△BOD周长的和.
04
课堂练习
【知识技能类作业】选做题:
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(1)△DEF在移动的过程中,若D、E两点始终在AC边上,
①F、C两点间的距离逐渐 ;连结FC,∠FCE的度数逐渐 .(填“不变”“变大”或“变小”)?
②∠FCE与∠CFE度数之和是否为定值,请加以说明;
变小
变大
②∠FCE与∠CFE度数之和为定值;
理由:∵∠FDE=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FCE+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;
04
课堂练习
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(2)△DEF在移动的过程中,如果D、E两点在AC的延长线上,那么∠FCE与∠CFE之间又有怎样的数量关系,请直接写出结论;
(2)如图,∠FCE与∠CFE度数之和为定值;?
理由:∵∠FDE=90°,∠DFE=45°,
又∵∠FDE+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FEG是△FEC的外角,
∴∠FCE+∠CFE=∠FEG=135°,
即∠FCE与∠CFE度数之和为定值;
04
课堂练习
【知识技能类作业】选做题:
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(3)能否将△DEF移动至某位置,使F、C的连线与BC垂直?求出∠CFE的度数.
(3)要使FC⊥BC,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.
05
课堂小结
平移的特征
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等, 对应角相等, 图形的形状和大小不变.
平移的特征
平移作图"四部曲":定、找、移、连
平移作图
2.如图,将△DEF沿FE方向平移3cm得到△ABC.若△DEF的周长为24cm,则四边形ABFD的周长为 cm.
1.如图,在△ABC中,∠ABC=90°,沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( )
A.EC=CF B.∠DEF=90° C.AC=DF D.AC∥DF
06
作业布置
【知识技能类作业】必做题:
A
30
06
作业布置
【知识技能类作业】必做题:
解:(1)由平移的特征知,∠????????????=∠????????????=70°.
?
3.如图,△DEF是由△ABC沿箭头方向平移得到的,已知∠ACB=70°,AC=10cm,EF=6cm,CE=2cm.
(1)求∠DFE的大小;
(2)求DF的长及点A移动的距离.
(2)????????=10????????,点A移动的距离为8????????.
?
4.如图,△ABC的边BC的长为4cm,将△ABC向上平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
06
作业布置
【知识技能类作业】选做题:
8
5.如图,将△ABC沿射线AB的方向平移2个单位长度到△DEF的位置,点A、B、C的对应点分别是点D、E、F.
(1)直接写出图中与AD相等的线段 ;
(2)若????????=3,则????????= ;
(3)若∠????????????=75°,求∠????????????的度数.
?
????????、????????
?
5
(3)由平移的特征知:????????∥????????,
5.如图,以BC为边的三角形共有( )
A.1个
B.2个
C.3个
D.4个
06
作业布置
【知识技能类作业】选做题:
C
06
作业布置
【综合拓展类作业】
解:(1)直线????????与????????互相平行,理由如下:
∵?????????∥????????,
∴∠????+?∠????????????=180°,
又∵∠????=∠???? ,
∴∠????????????+?∠????=180°,
∴?????????∥????????;
?
6.如图,已知直线 ????????∥????????,∠????=∠????=100°,点????、????在????????上,且满足∠????????????=∠????????????,????????平分∠????????????.
(1)直线????????与????????有何位置关系?请说明理由.
?
06
作业布置
【综合拓展类作业】
(2) ∵????????∥????????,
∴∠????????????=180°?∠????=80°,
∵∠????????????=∠????????????,????????平分∠????????????,
∴∠?????????????=12∠????????????+12∠????????????=12∠????????????=40°;
?
6.如图,已知直线 AB∥CD,∠A=∠C=100°,点E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(2)求∠DBE的度数.
06
作业布置
【综合拓展类作业】
(3) 存在. 设∠????????????=∠????????????=∠????????????=????°.
∵????????∥????????, ∴∠????????????=∠????????????=?????°+40°;
∵????????∥????????,
∴∠????????????=180°?∠????=80°,
∴∠????????????=80°?????°.
若∠????????????=∠????????????, 则????°+40°=80°?????°, 得????°=20°.
∴存在,∠????????????=∠????????????=60°.
?
6.如图,已知直线 AB∥CD,∠A=∠C=100°,点E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(3)若平行移动AD,在此过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出∠ADB的度数;若不存在,请说明理由.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
9.2.2平移的特征
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
能结合教材实例准确描述平移的特征; 能应用平移特征完成平移作图任务;
01
通过 "操作观察→数据测量→归纳验证" 的探究过程,经历从具体到抽象的数学建模,发展推理意识与几何直观;
02
发现平移特征在建筑设计、工业制造中的应用,体会数学对现实问题的解释力,增强应用意识.
03
02
复习导入
1.平移的定义: .
2.平移的两要素是 和 。
回顾旧知:
将一个图形沿着某个方向移动一定的距离的图形运动
方向
距离
你会用三角板、直尺画平行线吗?如果直尺是倾斜的,用三角板是否还能画出平行线?
03
新知探究
探究一
平移的特征
如图9.2.6, 在画平行线的时候, 有时为了需要, 将直尺和三角板放在倾斜的位置上. 但不管怎样, 我们总可以推得 A′B′∥AB, A′B′=AB, ∠B′=∠B.
同时也有A′C′∥ , A′C′ = , ∠C′ = .
B′C′与BC , B′C′ = , ∠A′ = .
A′C′
A′C′
∠C
平行
BC
∠A
你有什么发现?
03
新知探究
图形平移的特征:
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等, 对应角相等, 图形的形状和大小不变.
概括
(1)连结对应点的线段的长度就是平移距离(上述中的BB′);
(2)从原图上一点到其对应点的方向即起始点到终止点的方向为平移方向;
(3)平移前后图形的对应边平行且相等,对应角相等.
注意
03
新知探究
观察图9.2.7, △ABC沿着PQ方向平移到△A′B′C′的位置, 我们可以看到, △ABC上的每一点都作了相同的平移: A→A′, B→B′, C→C′.
你发现对应点所连的线段有什么特点了吗?
不难发现:
AA′∥BB′, AA′=BB′;
AA′∥ , AA′= ;
BB′与CC′ , BB′= .
BB′
BB′
平行
CC′
由此我们还可以得到:
平移后对应点所连的线段平行(或在同一条直线上)且相等.
概括
02
新知探究
将图9.2.8中的△ABC沿PQ方向平移到△A′B′C′的位置,其平移的距离为线段PQ的长度.
A
C
B
Q
P
A′
C′
B′
A
C
B
观察所得到的对应线段和对应点所连的线段是否符合上述我们所得到的平移的特征?
符合
03
例题讲解
解析:由于点A与点A′是一对对应点, 因此, 如图9.2.9②, 连结AA′,平移的方向就是点A到点A′的方向,平移的距离就是线段 AA′的长, 经测量可知,约25 mm .
如图9.2.9①所示,△ABC经过平移后到△A'B'C'的位置.指出平移的方向,并量出平移的距离. (精确到1mm)
例1
【总结】平移的距离就是一对对应点连线的长度.
03
新知探究
探究二
平移作图
试一试:在如图9.2.10的方格纸中,作出将图中的△ABC向右平移4格后的△A′B′C′,然后再作出将△A′B′C′向上平移3格后的△A′′B′′C′′. △A" B"C"是否可以看成是△ABC经过一次平移而得到的?如果是, 请指出平移的方向和距离.
可以看成是△ABC经过一次平移而得到的,平移方向是沿点C到点C"或点A到点A"或点B到点B"的方向,平移距离是线段CC"或线段AA"或线段BB"的长度.
03
新知讲解
平移作图的一般步骤:平移作图是平移基本性质的应用,利用平移可以得到许多美丽的图案,在具体作图时,应抓住作图的“四部曲”——定、找、移、连.
(1)定:确定平移的方向和距离;
(2)找:找出表示图形的关键点(图形的顶点、拐点、连结点);
(3)移:过关键点作平行且相等的线段,得到关键点的对应点;
(4)连:按原图顺次连结对应点.
02
新知探究
如图,在纸上画出△ABC和两条平行的直线m,n.先画出△ABC关于直线m对称的△A′B′C′,再画出△ABC关于直线n对称的△A″B″C″.观察△ABC和△A″B″C″,你能发现这两个三角形的关系吗?
03
新知讲解
【总结】经过两次翻折(对称轴互相平行)后得到的图形,可以看成是原图形经过平移得到的,即两次翻折相当于一次平移.
03
例题讲解
如图,在8×8的正方形网格中,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC先向右平移4个单位,再向上平移3个单位得△A1B1C1.
(1)作出平移后的△A1B1C1;
(2)求△A1B1C的面积.
例2
分析
(1)图形经过了几次平移?怎样作出多次平移后的图形?
(2)可直接求出△A1B1C的面积吗?△A1B1C的面积能转换成哪些图形面积的和(差)?
03
例题讲解
解析
(1)如图所示,△A1B1C1即为所求.
(2)由图可知,△A1B1C的面积为12×3×6?12×2×2?12×1×4?1×2=3.
?
03
新知讲解
【总结】此题主要考查了平移变换以及三角形面积求法等知识,根据题意正确把握平移的性质是解题关键.
作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连结对应点即可得到平移后的图形.
1.如图,直线AB∥CD,直线EF分别交AB、CD于点M、N.下列各角可以由∠END通过平移得到的角是( )
A.∠CNF B.∠AMF C.∠EMB D.∠AME
04
课堂练习
【知识技能类作业】必做题:
C
2.如图,将三角形ABC沿着PQ方向平移得到三角形A'B'C',则下列结论错误的是( )?
A.AB∥A'B' B.AA'=BB' C.AA'∥BB' D.AA'=AB
D
04
课堂练习
【知识技能类作业】必做题:
3.如图,平移方格纸中的图形,使点A平移到点A'处,画出平移后的图形.
解:如图所示
4.如果存在一条线把一个图形分割成两个部分,使其中一个部分沿某个方向平移后能与另一个部分重合,那么我们把这个图形叫做平移重合图形.下列图形中,平移重合图形是( )
A.平行四边形 B.等腰梯形 C.正六边形 D.圆
04
课堂练习
【知识技能类作业】选做题:
A
5.如图,一把直尺沿直线断开并发生平移,点E,D,B,F在同一条直线上,若∠DBC=62°,则∠ADE的度数为( )?
A.62° B.118° C.128° D.130°
B
6.如图,△ABC沿着BC方向平移得到△A'B'C',点P是直线AA'上任意一点,若△ABC,△PB'C'的面积分别为S1,S2,则下列关系正确的是( )
?
A.S1>S2 B.S1
课堂练习
【知识技能类作业】选做题:
C
04
课堂练习
【知识技能类作业】选做题:
解:(1)∵边AB沿着AC方向平移到ED,
∴AC∥DB,∴∠C=∠CBD=60°,
∵∠AEB=∠C+∠EBC,
∴∠EBC=70°-60°=10°;
(2)∵AB=ED,AE=DB,
∴△EOC与△BOD周长的和为CE+CO+EO+OD+OB+DB=DE+BC+EC+AE=AB+BC+AC=7+8+3=18.
7.如图,将△ABC中的边AB沿着AC方向平移到ED,ED交BC于点O,连结BD,BE.
(1)若∠AEB=70°,∠CBD=60°,求∠EBC的大小;
(2)若AB=7,BC=8,AC=3,边AB在平移的过程中,点E始终在边AC上(不与点A,点C重合),求△EOC与△BOD周长的和.
04
课堂练习
【知识技能类作业】选做题:
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(1)△DEF在移动的过程中,若D、E两点始终在AC边上,
①F、C两点间的距离逐渐 ;连结FC,∠FCE的度数逐渐 .(填“不变”“变大”或“变小”)?
②∠FCE与∠CFE度数之和是否为定值,请加以说明;
变小
变大
②∠FCE与∠CFE度数之和为定值;
理由:∵∠FDE=90°,∠DFE=45°,
又∵∠D+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FED是△FEC的外角,
∴∠FCE+∠CFE=∠FED=45°,
即∠FCE与∠CFE度数之和为定值;
04
课堂练习
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(2)△DEF在移动的过程中,如果D、E两点在AC的延长线上,那么∠FCE与∠CFE之间又有怎样的数量关系,请直接写出结论;
(2)如图,∠FCE与∠CFE度数之和为定值;?
理由:∵∠FDE=90°,∠DFE=45°,
又∵∠FDE+∠DFE+∠FED=180°,
∴∠FED=45°,
∵∠FEG是△FEC的外角,
∴∠FCE+∠CFE=∠FEG=135°,
即∠FCE与∠CFE度数之和为定值;
04
课堂练习
【知识技能类作业】选做题:
8.现有一副三角板,如图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°;图③中,将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动(移动开始时点D与点A重合).
(3)能否将△DEF移动至某位置,使F、C的连线与BC垂直?求出∠CFE的度数.
(3)要使FC⊥BC,则需∠FCE=∠A=30°,
又∵∠CFE+∠FCE=45°,
∴∠CFE=45°-30°=15°.
05
课堂小结
平移的特征
平移后的图形与原来图形的对应线段平行(或在同一条直线上)且相等, 对应角相等, 图形的形状和大小不变.
平移的特征
平移作图"四部曲":定、找、移、连
平移作图
2.如图,将△DEF沿FE方向平移3cm得到△ABC.若△DEF的周长为24cm,则四边形ABFD的周长为 cm.
1.如图,在△ABC中,∠ABC=90°,沿BC所在的直线向右平移得到△DEF,下列结论中不一定成立的是( )
A.EC=CF B.∠DEF=90° C.AC=DF D.AC∥DF
06
作业布置
【知识技能类作业】必做题:
A
30
06
作业布置
【知识技能类作业】必做题:
解:(1)由平移的特征知,∠????????????=∠????????????=70°.
?
3.如图,△DEF是由△ABC沿箭头方向平移得到的,已知∠ACB=70°,AC=10cm,EF=6cm,CE=2cm.
(1)求∠DFE的大小;
(2)求DF的长及点A移动的距离.
(2)????????=10????????,点A移动的距离为8????????.
?
4.如图,△ABC的边BC的长为4cm,将△ABC向上平移2cm得到△A'B'C',且BB'⊥BC,则阴影部分的面积为 cm2.
06
作业布置
【知识技能类作业】选做题:
8
5.如图,将△ABC沿射线AB的方向平移2个单位长度到△DEF的位置,点A、B、C的对应点分别是点D、E、F.
(1)直接写出图中与AD相等的线段 ;
(2)若????????=3,则????????= ;
(3)若∠????????????=75°,求∠????????????的度数.
?
????????、????????
?
5
(3)由平移的特征知:????????∥????????,
5.如图,以BC为边的三角形共有( )
A.1个
B.2个
C.3个
D.4个
06
作业布置
【知识技能类作业】选做题:
C
06
作业布置
【综合拓展类作业】
解:(1)直线????????与????????互相平行,理由如下:
∵?????????∥????????,
∴∠????+?∠????????????=180°,
又∵∠????=∠???? ,
∴∠????????????+?∠????=180°,
∴?????????∥????????;
?
6.如图,已知直线 ????????∥????????,∠????=∠????=100°,点????、????在????????上,且满足∠????????????=∠????????????,????????平分∠????????????.
(1)直线????????与????????有何位置关系?请说明理由.
?
06
作业布置
【综合拓展类作业】
(2) ∵????????∥????????,
∴∠????????????=180°?∠????=80°,
∵∠????????????=∠????????????,????????平分∠????????????,
∴∠?????????????=12∠????????????+12∠????????????=12∠????????????=40°;
?
6.如图,已知直线 AB∥CD,∠A=∠C=100°,点E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(2)求∠DBE的度数.
06
作业布置
【综合拓展类作业】
(3) 存在. 设∠????????????=∠????????????=∠????????????=????°.
∵????????∥????????, ∴∠????????????=∠????????????=?????°+40°;
∵????????∥????????,
∴∠????????????=180°?∠????=80°,
∴∠????????????=80°?????°.
若∠????????????=∠????????????, 则????°+40°=80°?????°, 得????°=20°.
∴存在,∠????????????=∠????????????=60°.
?
6.如图,已知直线 AB∥CD,∠A=∠C=100°,点E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(3)若平行移动AD,在此过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出∠ADB的度数;若不存在,请说明理由.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
