第24-26章阶段测试卷（含解析）

中小学教育资源及组卷应用平台
第24-26章阶段测试卷-2024-2025学年数学九年级下册沪科版
一、单选题
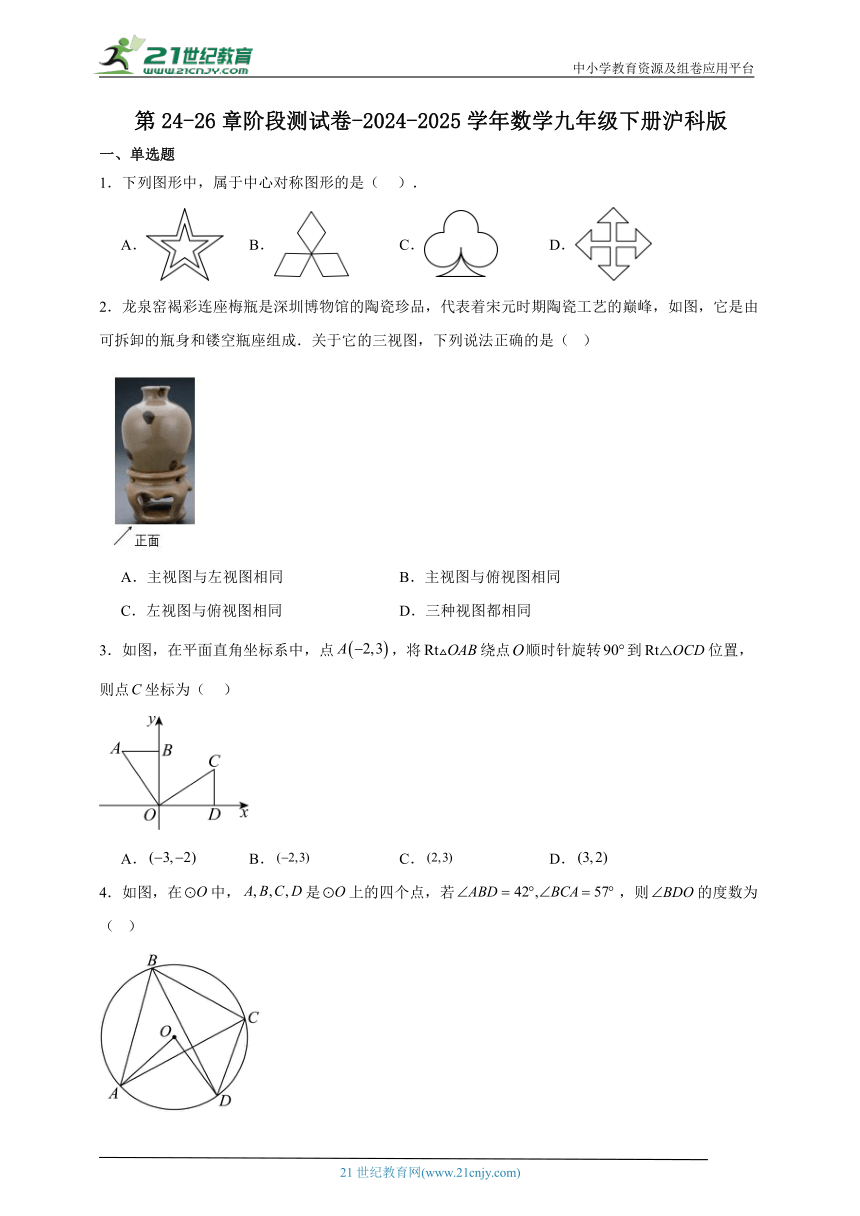
1．下列图形中，属于中心对称图形的是（ ）．
A． B． C． D．
2．龙泉窑褐彩连座梅瓶是深圳博物馆的陶瓷珍品，代表着宋元时期陶瓷工艺的巅峰，如图，它是由可拆卸的瓶身和镂空瓶座组成．关于它的三视图，下列说法正确的是（ ）
A．主视图与左视图相同 B．主视图与俯视图相同
C．左视图与俯视图相同 D．三种视图都相同
3．如图，在平面直角坐标系中，点，将绕点顺时针旋转到位置，则点坐标为（ ）
A． B． C． D．
4．如图，在中，是上的四个点，若，则的度数为（ ）
A． B． C． D．
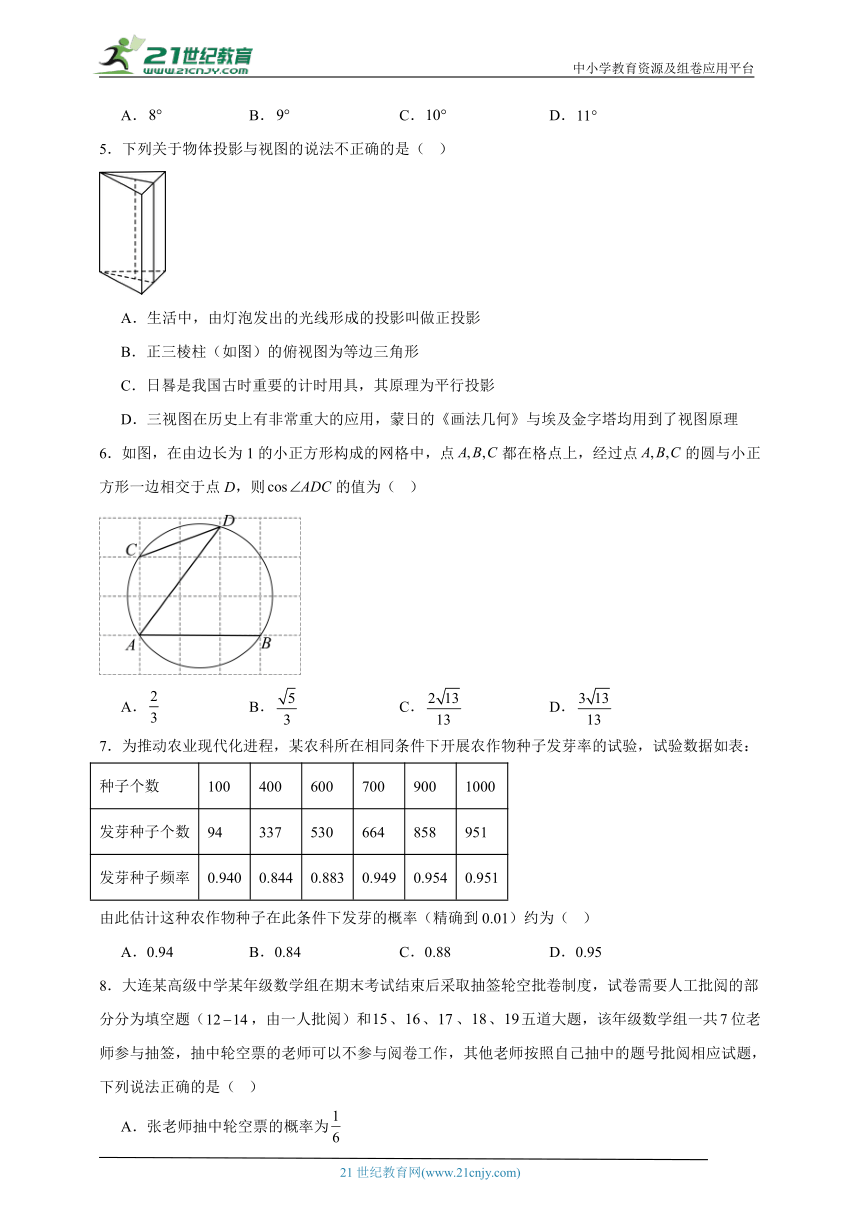
5．下列关于物体投影与视图的说法不正确的是（ ）
A．生活中，由灯泡发出的光线形成的投影叫做正投影
B．正三棱柱（如图）的俯视图为等边三角形
C．日晷是我国古时重要的计时用具，其原理为平行投影
D．三视图在历史上有非常重大的应用，蒙日的《画法几何》与埃及金字塔均用到了视图原理
6．如图，在由边长为1的小正方形构成的网格中，点都在格点上，经过点的圆与小正方形一边相交于点D，则的值为（ ）
A． B． C． D．
7．为推动农业现代化进程，某农科所在相同条件下开展农作物种子发芽率的试验，试验数据如表：
种子个数 100 400 600 700 900 1000
发芽种子个数 94 337 530 664 858 951
发芽种子频率 0.940 0.844 0.883 0.949 0.954 0.951
由此估计这种农作物种子在此条件下发芽的概率（精确到0.01）约为（ ）
A．0.94 B．0.84 C．0.88 D．0.95
8．大连某高级中学某年级数学组在期末考试结束后采取抽签轮空批卷制度，试卷需要人工批阅的部分分为填空题（，由一人批阅）和、、、、五道大题，该年级数学组一共位老师参与抽签，抽中轮空票的老师可以不参与阅卷工作，其他老师按照自己抽中的题号批阅相应试题，下列说法正确的是（ ）
A．张老师抽中轮空票的概率为
B．夏老师抽中批阅题的概率为
C．刚开始，王老师和常老师首先同时进行抽签，则在互不影响的前提下，王老师批阅题，常老师轮空的概率为
D．已知王老师第一个抽到了题，夏老师第二个抽到了题，则此时常老师和张老师同时抽票，则张老师抽到轮空票的概率为
二、填空题
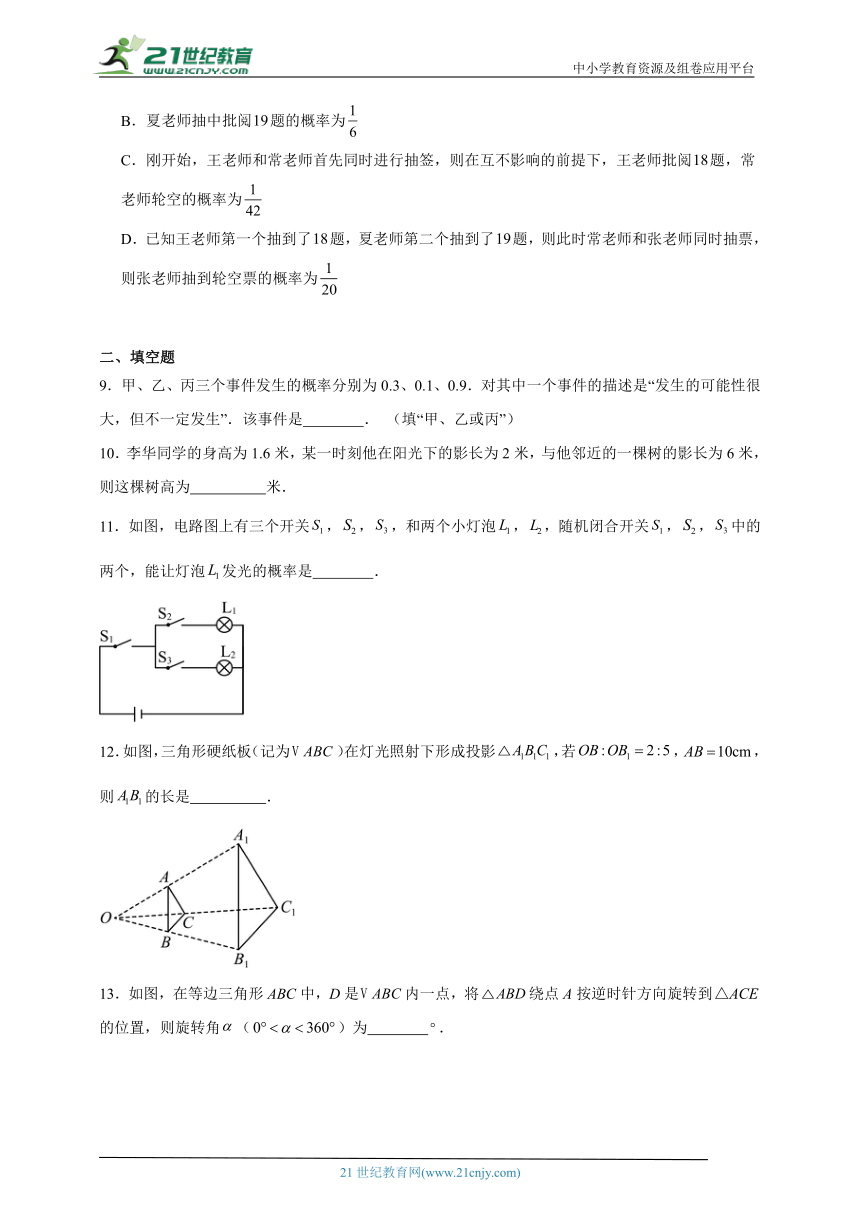
9．甲、乙、丙三个事件发生的概率分别为0.3、0.1、0.9．对其中一个事件的描述是“发生的可能性很大，但不一定发生”．该事件是 ． （填“甲、乙或丙”）
10．李华同学的身高为1.6米，某一时刻他在阳光下的影长为2米，与他邻近的一棵树的影长为6米，则这棵树高为 米．
11．如图，电路图上有三个开关，，，和两个小灯泡，，随机闭合开关，，中的两个，能让灯泡发光的概率是 ．
12．如图，三角形硬纸板（记为）在灯光照射下形成投影，若，，则的长是 ．
13．如图，在等边三角形ABC中，D是内一点，将绕点A按逆时针方向旋转到的位置，则旋转角（）为 ．
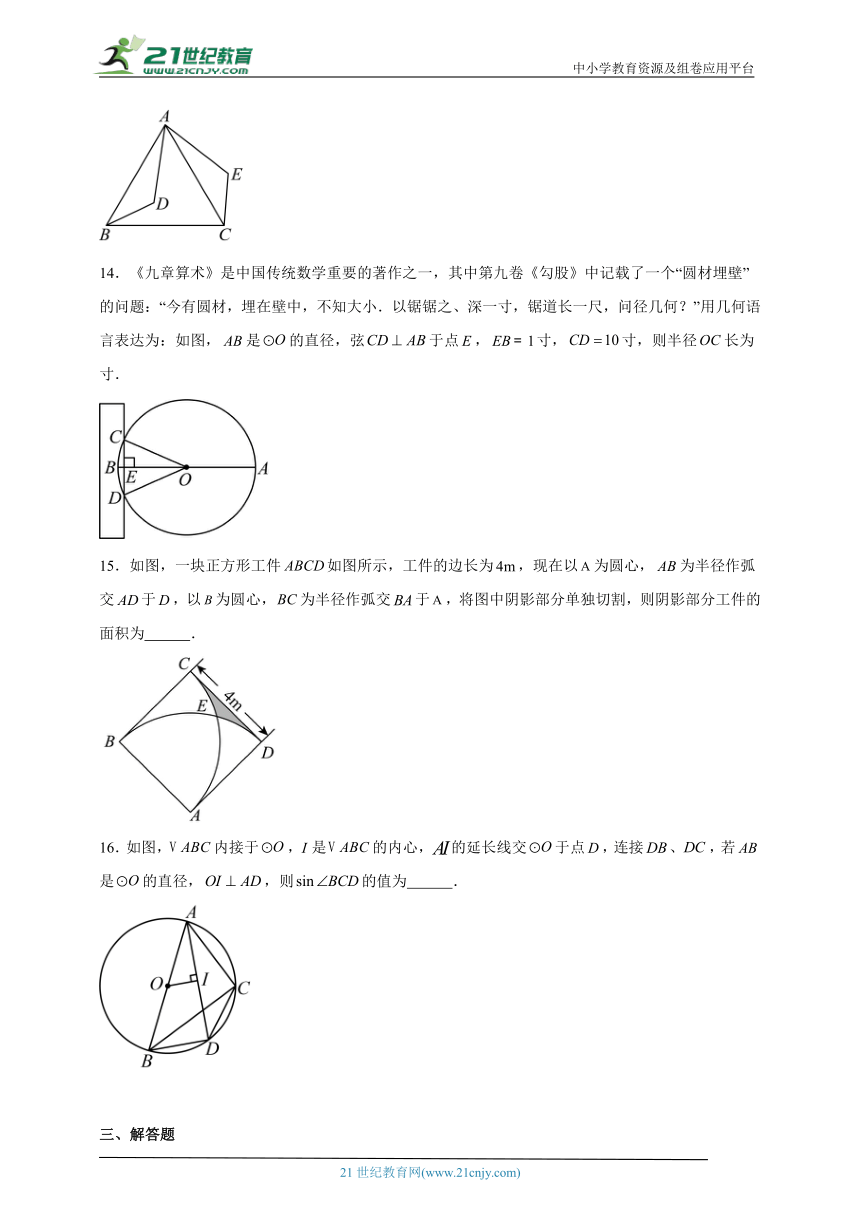
14．《九章算术》是中国传统数学重要的著作之一，其中第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材，埋在壁中，不知大小．以锯锯之、深一寸，锯道长一尺，问径几何？”用几何语言表达为：如图，是的直径，弦于点，寸，寸，则半径长为 寸．
15．如图，一块正方形工件如图所示，工件的边长为，现在以为圆心，为半径作弧交于，以为圆心，为半径作弧交于，将图中阴影部分单独切割，则阴影部分工件的面积为 ．
16．如图，内接于，是的内心，的延长线交于点，连接、，若是的直径，，则的值为 ．
三、解答题
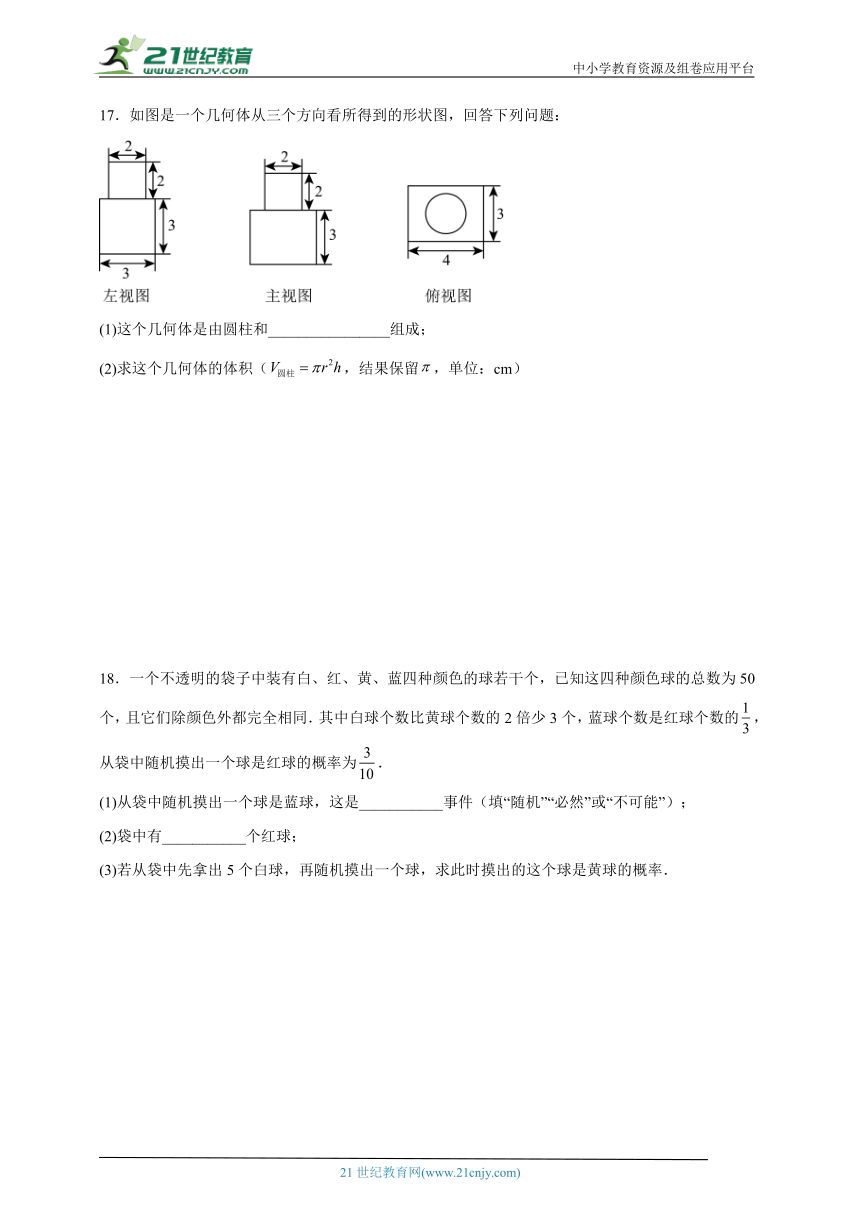
17．如图是一个几何体从三个方向看所得到的形状图，回答下列问题：
(1)这个几何体是由圆柱和________________组成；
(2)求这个几何体的体积（，结果保留，单位：cm）
18．一个不透明的袋子中装有白、红、黄、蓝四种颜色的球若干个，已知这四种颜色球的总数为50个，且它们除颜色外都完全相同．其中白球个数比黄球个数的2倍少3个，蓝球个数是红球个数的，从袋中随机摸出一个球是红球的概率为．
(1)从袋中随机摸出一个球是蓝球，这是___________事件（填“随机”“必然”或“不可能”）；
(2)袋中有___________个红球；
(3)若从袋中先拿出5个白球，再随机摸出一个球，求此时摸出的这个球是黄球的概率．
19．如图，是的直径，，点E在的延长线上，且与相交于点F．
(1)求证：是的切线；
(2)若的半径为，求的长．
20．（1）如图1，在中，，，的平分线交于点D．过点D分别作，．垂足分别为E，F．则四边形是什么形状？请求证 ．
（2）如图2，是半圆O的直径，．P是上一点，且，连接，的平分线交于点C，过点C分别作，，垂足分别为E，F，求线段的长．
21．2024年10月31日8时11分，神舟十六号载人飞船返回舱在东风着陆场成功着陆．某中学为了提高学生对航天的认识，在全校开展了主题为“弘扬航天精神”的知识竞赛活动．为了解学生竞赛情况，学校从中随机抽取了部分参赛学生的成绩，整理并绘制出如下两幅不完整的统计图表．
请根据图表信息解答以下问题：
(1)本次调查随机抽取了____名参赛学生的成绩，在扇形统计图中F组所在扇形的圆心角是____度；
(2)补全频数分布直方图；
(3)成绩前四名的学生中正好是两名男生和两名女生，若从这四名学生中任意选两人为该校的航天知识宣传员，求恰好选中一名男生和一名女生的概率．
22．如图，点A、E在上，与的夹角为，连结，过A点作的切线．
(1)试求的度数（用含有n的代数式表示）；
(2)在的延长线上取一点D，以线段为一边作矩形，点C在射线上．
①当时，在n的变化过程中，探究线段与、之间是否存在某固定的数量关系？若存在，试求出它们的数量关系；若不存在，请说明理由；
②连结，当时，试求出的值．
23．正方形的边长为4，以为弦作，点为边上一动点．
(1)已知经过三点．
①如图1，若，判断边所在直线与的位置关系，并说明理由；
②如图2，是的中点，交射线于点，当平分时，求四边形的面积；
(2)如图3，若是圆的直径，是中点，与圆交于点，连接，求的值．
(3)如图4，与边相切于是延长线上一点，是直线下方一点，且满足是的中点，连接交于点，当点在内时，求的值（用表示），并求出的取值范围．
《第24-26章阶段测试卷-2024-2025学年数学九年级下册沪科版》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A D B A D D C
1．D
【分析】本题主要考查了中心对称图形的定义，根据中心对称图形的定义进行逐一判断即可：把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
【详解】解：A、不是中心对称图形，不符合题意；
B、不是中心对称图形，不符合题意；
C、不是中心对称图形，不符合题意；
D、是中心对称图形，符合题意；
故选：D．
2．A
【分析】本题主要考查了简单几何体的三视图；直接利用已知几何体分别得出三视图进而分析得出答案．熟知三视图的定义是关键．
【详解】解：观察可知，由于该几何体的对称性主视图与左视图相同，俯视图看不到几何体的下部分，但是能看到瓶口，即俯视图与其它两种视图不相同，
故选；A．
3．D
【分析】本题主要考查了旋转的性质，平面直角坐标系内点的坐标，
根据点可知，再结合旋转的性质得，然后根据点C在第一象限得出答案．
【详解】解：∵点，
∴，
由旋转的性质得，
∴点．
故选：D.
4．B
【分析】本题考查了同弧或等弧所对圆周角相等，直径所对圆周角为直角，圆内接四边形的性质，直角三角形两锐角互余等知识，掌握同弧或等弧所对圆周角相等，直径所对圆周角为直角，圆内接四边形的性质，合理作出辅助线是解题的关键．
如图所示，延长交于点，连接，得到是直角三角形，根据题意得到，，四边形是内接四边形，，在中由直角三角形两锐角互余即可求解．
【详解】解：如图所示，延长交于点，连接，
∵是直径，
∴是直角三角形，
∵，
∴，
∴，
∵点在上，
∴四边形是内接四边形，
∴，
在中，，
故选：B ．
5．A
【分析】本题主要考查投影，熟练掌握投影与视图是解题的关键．根据投影和视图的定义进行判断即可．
【详解】解：生活中，由灯泡发出的光线形成的投影不叫做正投影，故选项A错误，符合题意；
正三棱柱（如图）的俯视图为等边三角形，故选项B正确，不符合题意；
日晷是我国古时重要的计时用具，其原理为平行投影，故选项C正确，不符合题意；
三视图在历史上有非常重大的应用，蒙日的《画法几何》与埃及金字塔均用到了视图原理，故选项D正确，不符合题意；
故选A．
6．D
【分析】本题考查了圆周角定理的推论，勾股定理，锐角三角函数的定义，解答本题的关键是利用圆周角定理的推论把求的余弦值转化成求的余弦值，本题是一道比较不错的习题．
首先根据圆周角定理的推论可知，，然后在中，根据锐角三角函数的定义求出．
【详解】解：如图，连接、．
和所对的弧长都是，
根据圆周角定理的推论知，．
∵
∴为直径，
在中，根据锐角三角函数的定义知，
，
，，
，
．
故选：D．
7．D
【分析】本题主要考查利用频率估计概率，概率是大量重复试验的情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率．
【详解】解：∵观察表格，发现大量重复试验发芽的频率逐渐稳定在0.95左右，
∴估计这种农作物种子在此条件下发芽的概率约为0.95．
故选：D．
8．C
【分析】先理清所有等可能的抽签结果，再结合具体情况具体分析事件概率即可．
【详解】解：依题得，共有七种抽签结果：填空题、题、题、题、题、题、轮空，
张老师抽中轮空票的概率为，选项错误；
夏老师抽中批阅题的概率为，选项错误；
刚开始，王老师和常老师首先同时进行抽签，则在互不影响的前提下，求王老师批阅题，常老师轮空的概率，
即在王老师批阅题的前提下，常老师轮空，概率应计算为，选项正确；
已知王老师第一个抽到了题，夏老师第二个抽到了题，还剩下五种抽签结果，
则此时常老师和张老师同时抽票，则张老师抽到轮空票的概率为，选项错误
故选：．
【点睛】本题考查的知识点是列举随机实验的所有可能结果、根据概率公式计算概率，解题关键是理清所有等可能的抽签结果．
9．丙
【分析】根据概率的意义，概率公式，即可解答．本题考查了概率的意义，概率公式，熟练掌握概率的意义是解题的关键．
【详解】解：∵甲、乙、丙三个事件发生的概率分别为0.3、0.1、0.9，且0.9非常接近，
∴对其中一个事件的描述是“发生的可能性很大，但不一定发生”．
即该事件是丙，
故答案为：丙．
10．4.8
【分析】本题考查平行投影及相似三角形的性质．关键是理解平行投影的特点：两个物体竖直放在地面上，两个物体及它们各自的影子及光线构成的两个直角三角形相似，利用相似的性质求解.
利用平行投影的特征以及相似三角形的性质可求出答案．
【详解】解：假设树高为，
由题意可知：，
解得：，即树高．
故答案为：4.8．
11．
【分析】本题主要考查了树状图法或列表法求解概率，树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步或两步以上完成的事件．正确画出树状图是解题的关键．
先画出树状图，得到所有的等可能的结果数，再找到能让灯泡发光的结果数，最后依据概率计算公式求解即可．
【详解】解：画树状图如下：
共有6种等可能的结果，其中能让灯泡发光的结果数为2，
∴能让灯泡发光的概率为：，
故答案为：．
12．
【分析】本题考查中心投影的定义和性质，位似三角形的性质，熟练掌握中心投影和位似三角形的性质是解题的关键．利用中心投影得定义可得与是位似三角形，再利用位似三角形的性质求解即可．
【详解】解：由中心投影的定义可得与是位似三角形，
∴，且由位似得，
∴，
得：，
故答案为：．
13．60
【分析】本题考查旋转变换，等边三角形的性质，根据旋转角即为的度数，然后根据等边三角形的性质求出即可．
【详解】解：∵是等边三角形，
∴，
又∵绕点A按逆时针方向旋转到，
∴旋转角为，
故答案为：．
14．13
【分析】本题考查垂径定理，勾股定理的应用等知识，解题的关键是学会利用参数构建方程解决问题．设寸，利用垂径定理得到，利用勾股定理得到，根据其建立方程求解，即可解题．
【详解】解：设寸，
弦于点，寸，寸，
寸，
，
，
解得，
半径长为寸．
故答案为：13．
15．
【分析】本题考查了正方形的性质，等边三角形的判定和性质，扇形面积的计算，掌握扇形面积的计算是关键．
根据题意，，以为圆心，为半径作弧交于，以为圆心，为半径作弧交于，如图所示，两弧交于点，连接，过点作于点，是等边三角形，则，，则，由此即可求解．
【详解】解：∵四边形是正方形，
∴，
∵以为圆心，为半径作弧交于，以为圆心，为半径作弧交于，如图所示，两弧交于点，连接，过点作于点，
∴，
∴是等边三角形，
∴，
∴，
∴，则，
∴，则，
∴阴影部分的面积，
故答案为： ．
16．/
【分析】根据条件证得，可得，由是的直径，得到，由于，于是求得，设，根据勾股定理即可得到 ，根据三角函数即可得出答案．
【详解】解：连接，
点是的内心，
，，
，
，
，
，，
，
，
设
是的直径，
，
，
，
，
，
，
，
，
，
故答案为：．
【点睛】本题考查了三角形的内切圆和内心，三角形的外接圆和外心，垂径定理，圆周角定理，三角形外角性质，等腰三角形的判定等知识点的应用，能正确作出辅助线并求出是解此题的关键．
17．(1)长方体
(2)
【分析】本题主要考查了几何体的三视图，求圆柱的体积，
对于（1），观察三视图可知组合体上面是一个圆柱，下面是一个长方体；
对于（2），根据体积公式求解即可．
【详解】（1）解：观察组合体上面是一个圆柱，下面是一个长方体.
故答案为：长方体；
（2）解：该几何体上部分是一个圆柱，底面直径是、高是；下部分是一个长方体，长、宽、高分别是.
∴，
∴该几何体的体积为．
18．(1)随机
(2)15
(3)
【分析】本题考查了事件的分类，利用概率求数量，一元一次方程的应用，熟练利用概率公式求数量是解题的关键．
（1）根据事件的分类可得从袋中随机摸出一个球是蓝球是随机事件；
（2）利用概率求数量即可；
（3）计算黄球的个数即可解答．
【详解】（1）解：从袋中随机摸出一个球是蓝球是随机事件，
故答案为：随机；
（2）解：个，
故袋中有个红球，
故答案为：；
（3）解：蓝球个数是红球个数的，
蓝球个数为个，
设黄球的个数为个，则白球的个数为个，
可得，
解得，
故袋中有黄球个，
从袋中先拿出5个白球，此时袋中有个球，
此时摸出的这个球是黄球的概率为．
19．(1)见解析
(2)
【分析】（1）连接，，证明垂直平分，得出，证明，得出，说明，即可证明结论；
（2）根据是的直径，得出，根据勾股定理求出，根据三角函数定义求出，得出，求出，即可得到的长．
【详解】（1）证明：连接，，如图所示：
∵，
∴，
∵，
∴点O、B在的垂直平分线上，
∴垂直平分，
∴，
∵，
∴，
∴，
∴，
∵是的直径，
∴是的切线；
（2）连接，
解：∵的半径为3，
∴，
∵是的直径，
∴，
∵，
∴，
∴，
∴
∴，
∴，
∴
【点睛】本题主要考查了切线的判定，勾股定理，解直角三角形，圆周角定理，垂直平分线的判定等知识，解题的关键是作出辅助线，熟练掌握相关的判定和性质．
20．（1）正方形，见解析；（2）
【分析】（1）根据角平分线的性质，结合正方形的判定定理即可求解；
（2）连接，可证明是等边三角形，则可求，由（1）知，，则，在中，，可得方程，求出，即可求；
【详解】解：（1）∵，，
∴ ，
∵，
∴四边形是矩形，
∵平分，
∴ ，
∴矩形是正方形．
（2）连接，
是半圆的直径，，
，
，
，
是等边三角形，
，
，
，，
且在中，，
∵四边形是正方形，
，
，
，
解得：，
．
【点睛】该题主要考查了正方形的性质和判定，等边三角形的性质和判定，直角三角形的性质，角平分线的性质，圆中相关性质等知识点，解题的关键是掌握以上知识点．
21．(1)50，28.8
(2)见解析
(3)
【分析】本题考查频数分布直方图，扇形统计图以及列表法或树状图法求概率，掌握频率= 频数总数 ，列举所有可能出现的结果是解决问题的关键．
（1）根据C的频数和所占的百分比，进行计算即可；求出F组所占的百分比即可求出相应的圆心角度数；
（2）求出D组的频数即可补全条形统计图；
（3）列举出所有可能出现的结果，进而求出选择一男一女的概率．
【详解】（1）解：（人），
；
故答案为：50，28.8；
（2）（人），
补全图形如下：
（3）画树状图如下：
共有12个等可能的结果，恰好选中一名男生和一名女生的结果有8个，
∴恰好选中一名男生和一名女生的概率为．
22．(1)
(2)①存在，；②
【分析】（1）由题意易得，然后根据切线的性质可进行求解；
（2）①连结交于点，由题意易得，则有，然后可得，进而根据全等三角形的性质可进行求解；
②连结，由题意先得到点在线段上，过作，垂足为，则，，然后可得，进而根据相似三角形的性质可进行求解．
【详解】（1）解：∵，
∴，
∵是的切线，
∴，
∴；
（2）解：①存在，；
连结交于点，
在矩形中，，，
又∵，
∴，
∵，
∴，
∴，
∵，，
∴，
在和中，
∴，
∴，
∵，
∴；
②连结，
∵，
∴不妨设，则，，，
，
又，
，
点在线段上；
过作，垂足为，则，，
方法一：
又矩形中，，
，
，
，，
，
，
，
在矩形中，，，
；
方法二：
，，
，
，
设，则，
，
在中，，
在中，，
，
解得，
，，
在矩形中，，
．
【点睛】本题主要考查切线的性质、勾股定理、等腰三角形的性质、矩形的性质及相似三角形的性质与判定，熟练掌握切线的性质、勾股定理、等腰三角形的性质、矩形的性质及相似三角形的性质与判定是解题的关键．
23．(1)①直线与相切，理由见解析②
(2)
(3)，
【分析】（1）①过点作，连接，延长交于点，证明四边形为矩形，得到，圆周角定理的推论得到为的直径，勾股定理求出的长，垂径定理结合三角形的中位线定理求出的长，进而求出的长，比较与半径的大小关系即可得出结论；
②连接，延长交于点，证明，求出的长，圆周角定理结合等弧对等弦，设，解直角三角形求出，根据，求出的值，进而利用分割法求出四边形的面积即可；
（2）连接并延长交于点，过点作，勾股定理求出的长，证明，等积法求出的长，进而求出的长，证明，求出的长，勾股定理求出的长，再利用正弦的定义进行求解即可；
（3）连接，过点作，连接，延长交于点，由切线的性质，推出四边形为矩形，求出的长，证明为等边三角形，由三线合一得到的长，进而求出的长，由平行线分线段成比例，得到，进而求出的值，由三角形的中位线定理，求出的长，根据点在圆内，求出的取值范围即可．
【详解】（1）解：直线与相切，理由如下：
过点作，连接，延长交于点，如图：
∵正方形，
∴，
∴四边形为矩形，
∴，
∵经过三点，，
∴为的直径，
∵，
∴，
∴的半径为，
∵，
∴，
∴，
∴，
∴点到直线的距离等于的半径，
∴直线与相切；
②连接，延长交于点，
∵，
∴，
∴，
∵为的中点，
∴，
∴，
∴，
∴，，
∴，
由①可知，为的直径，
∴，
∵平分，
∴，
∴，
∴，
设，
∵，
∴，
∴，
∴，
∴，
∴，
∴四边形的面积为；
（2）解：连接并延长交于点，过点作，
∵为的中点，
∴，
在中，，
∵为直径，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∴，
∵，即：，
∴，
∴，
∵，
∴，
∴，
∴，
∴，
∴，
∴；
（3）连接，过点作，连接，延长交于点，
∵为切线，
∴，
∵，
∴四边形为矩形，
∴，，，
∴，
∴，
∵，
∴为等边三角形，
∴，
∴，
∵为的中点，
∴，
∵，
∴，
∴，即：，
∴，
即；
∵，为的中点，
∴，
连接，设的半径为，
∴，，
在中，由勾股定理，得：，
解得：，
∴的半径为，
∵点在内，
∴，
即：，
∴．
【点睛】本题考查正方形的性质，全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形，切线的性质，判断直线和圆的位置关系，圆周角定理等知识点，熟练掌握相关知识点，合理添加辅助线，是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)