乘法公式的几何背景 题型练习 (含答案)2024-2025学年沪科版七年级数学下册
文档属性
| 名称 | 乘法公式的几何背景 题型练习 (含答案)2024-2025学年沪科版七年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 115.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
乘法公式的几何背景 题型练习
类型一 完全平方公式的几何背景
1.(2024 山东济南历城期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1 所示的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b 的正方形,C种纸片是长为b、宽为a的长方形.并用A 种纸片一张,B种纸片一张,C种纸片两张拼成如图2所示的大正方形.
(1)请用两种不同的方法表示图2中大正方形的面积:
方法1: ;
方法2: .
(2)观察图2,请你写出三个代数式( b , ab之间的数量关系: .
(3)根据(2)中的等量关系,解决下列问题:
①已知 求 ab的值;
②已知( 求(2023-a)(a-2021)的值.
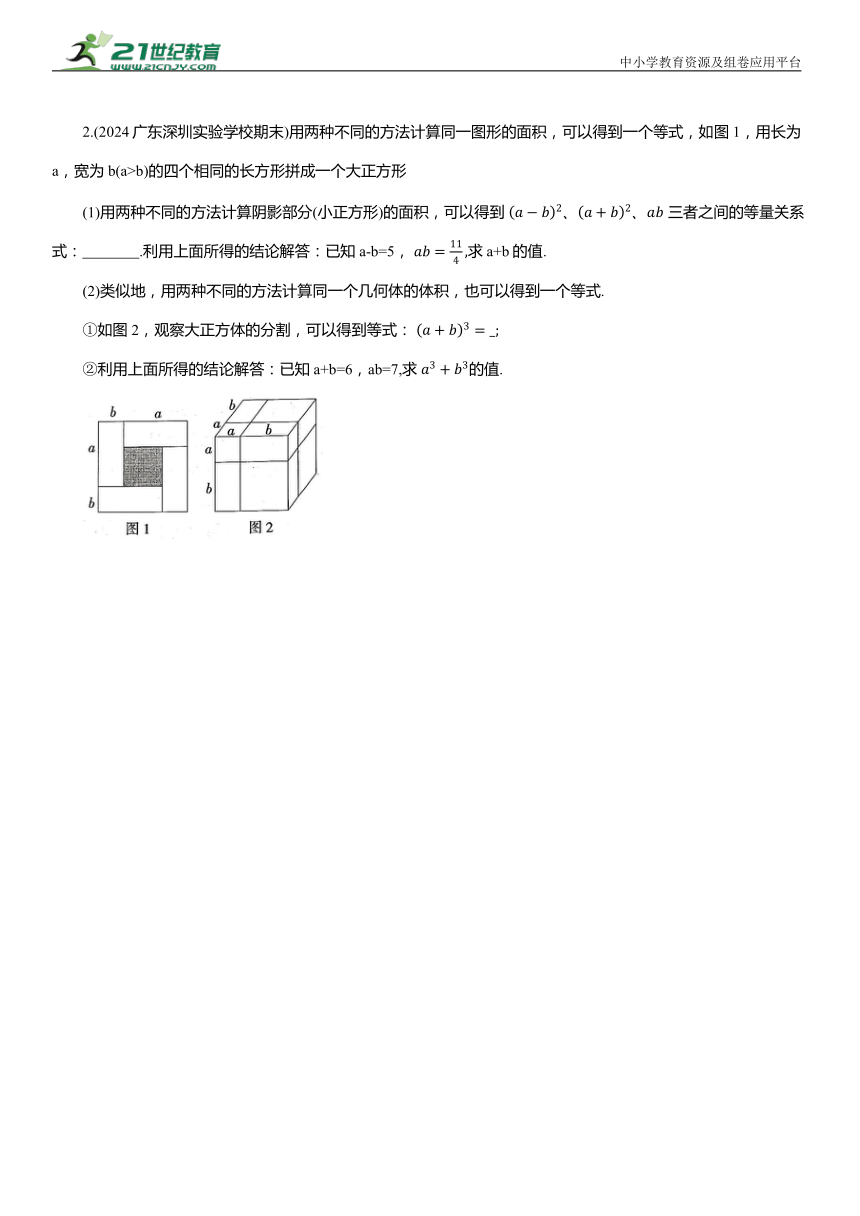
2.(2024广东深圳实验学校期末)用两种不同的方法计算同一图形的面积,可以得到一个等式,如图1,用长为a,宽为b(a>b)的四个相同的长方形拼成一个大正方形
(1)用两种不同的方法计算阴影部分(小正方形)的面积,可以得到 三者之间的等量关系式: .利用上面所得的结论解答:已知a-b=5, 求a+b的值.
(2)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式.
①如图2,观察大正方体的分割,可以得到等式:
②利用上面所得的结论解答:已知a+b=6,ab=7,求 的值.
类型二 平方差公式的几何背景
3.(2024河北石家庄二十八中模拟)如图 1 所示,两个长方形用不同的形式拼成图2和图3两个图形
(1)图2中阴影部分的面积为 则图3 中阴影部分的面积为 .(用含字母a,b的式子且不同于图2的方式表示)
(2)由(1)你可以得到的乘法公式为 .
(3)根据你所得到的乘法公式解决下面的问题:
计算:①103×97;
②(a+2b-c)(a-2b-c).
4.如图1,在一个边长为a的正方形木板上锯掉一个边长为b的正方形,并把余下的部分沿虚线锯开拼成如图2所示的图形.
(1)请用两种方法表示阴影部分的面积:由图1得 ;由图2得 .
(2)由图1与图2阴影部分的面积关系,可以得到一个等式: .
(3)利用(2)中的等式,已知 且a+b=8,求a-b的值.
①解析
(3)①因为 且
所以49=33+2ab,解得 ab=8.
②设2023-a=m,a-2021=n,
则m +n =8,m+n=2023-a+a-2021=2,
因为 所以4=8+2mn,
解得 mn=-2,
则(2023-a)(a-2021)的值为-2.
②解析 (1)由题图1可知,小正方形的边长为a-b,所以题图1中阴影部分的面积可表示为(
题图1中大正方形的面积为( ,四个小长方形的面积之和为4ab,所以题图1中阴影部分的面积可表示为
由此可得,
因为
所以
所以a+b=6(舍负).
(2)①由题图2可知,大正方体的体积可表示为(a+b) .
大正方体的体积还可表示为八个小长方体的体积之和,即
所以
故答案为
②因为a+b=6, ab=7,
所以
故
③解析 ((1)(a+b)(a-b).
(3)①103×97=(100+3)×(100-3)= 100 -3 =10 000-9=9991.
②(a+2b-c)(a-2b-c)=[(a-c)+2b][(a-c)-2b]
④ 解析 (1)题图1中阴影部分的面积为 题图2中阴影部分的面积为 即(a+b)(a-b).故答案为a -b ;(a+b)(a-b).
(3)因为 且a+b=8,
所以(a+b)(a-b)=16,即8(a-b)=16,
所以a-b=2.
乘法公式的几何背景 题型练习
类型一 完全平方公式的几何背景
1.(2024 山东济南历城期末)乘法公式的探究及应用:
数学活动课上,老师准备了若干个如图1 所示的三种纸片:A种纸片是边长为a的正方形,B种纸片是边长为b 的正方形,C种纸片是长为b、宽为a的长方形.并用A 种纸片一张,B种纸片一张,C种纸片两张拼成如图2所示的大正方形.
(1)请用两种不同的方法表示图2中大正方形的面积:
方法1: ;
方法2: .
(2)观察图2,请你写出三个代数式( b , ab之间的数量关系: .
(3)根据(2)中的等量关系,解决下列问题:
①已知 求 ab的值;
②已知( 求(2023-a)(a-2021)的值.
2.(2024广东深圳实验学校期末)用两种不同的方法计算同一图形的面积,可以得到一个等式,如图1,用长为a,宽为b(a>b)的四个相同的长方形拼成一个大正方形
(1)用两种不同的方法计算阴影部分(小正方形)的面积,可以得到 三者之间的等量关系式: .利用上面所得的结论解答:已知a-b=5, 求a+b的值.
(2)类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式.
①如图2,观察大正方体的分割,可以得到等式:
②利用上面所得的结论解答:已知a+b=6,ab=7,求 的值.
类型二 平方差公式的几何背景
3.(2024河北石家庄二十八中模拟)如图 1 所示,两个长方形用不同的形式拼成图2和图3两个图形
(1)图2中阴影部分的面积为 则图3 中阴影部分的面积为 .(用含字母a,b的式子且不同于图2的方式表示)
(2)由(1)你可以得到的乘法公式为 .
(3)根据你所得到的乘法公式解决下面的问题:
计算:①103×97;
②(a+2b-c)(a-2b-c).
4.如图1,在一个边长为a的正方形木板上锯掉一个边长为b的正方形,并把余下的部分沿虚线锯开拼成如图2所示的图形.
(1)请用两种方法表示阴影部分的面积:由图1得 ;由图2得 .
(2)由图1与图2阴影部分的面积关系,可以得到一个等式: .
(3)利用(2)中的等式,已知 且a+b=8,求a-b的值.
①解析
(3)①因为 且
所以49=33+2ab,解得 ab=8.
②设2023-a=m,a-2021=n,
则m +n =8,m+n=2023-a+a-2021=2,
因为 所以4=8+2mn,
解得 mn=-2,
则(2023-a)(a-2021)的值为-2.
②解析 (1)由题图1可知,小正方形的边长为a-b,所以题图1中阴影部分的面积可表示为(
题图1中大正方形的面积为( ,四个小长方形的面积之和为4ab,所以题图1中阴影部分的面积可表示为
由此可得,
因为
所以
所以a+b=6(舍负).
(2)①由题图2可知,大正方体的体积可表示为(a+b) .
大正方体的体积还可表示为八个小长方体的体积之和,即
所以
故答案为
②因为a+b=6, ab=7,
所以
故
③解析 ((1)(a+b)(a-b).
(3)①103×97=(100+3)×(100-3)= 100 -3 =10 000-9=9991.
②(a+2b-c)(a-2b-c)=[(a-c)+2b][(a-c)-2b]
④ 解析 (1)题图1中阴影部分的面积为 题图2中阴影部分的面积为 即(a+b)(a-b).故答案为a -b ;(a+b)(a-b).
(3)因为 且a+b=8,
所以(a+b)(a-b)=16,即8(a-b)=16,
所以a-b=2.
