期末素养综合测试 (一) (含答案)2024-2025学年沪科版七年级数学下册
文档属性
| 名称 | 期末素养综合测试 (一) (含答案)2024-2025学年沪科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 176.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:05:42 | ||
图片预览



文档简介
期末素养综合测试 (一)
一、选择题(每小题3分,共30分)
1.(2024 四川遂宁中考)下列各数中,无理数是( )
A.-2 B. C . D.0
2.(2024安徽马鞍山和县期末)使分式 有意义的x的取值范围为 ( )
A. x≠-1 B. x≠1
C. x≠2 D. x≠-1且x≠2
3.(2024安徽池州贵池期末)下列图形中可以由一个基础图形通过平移变换得到的是 ( )
4.(2024吉林长春中考)下列运算一定正确的是( )
A.2a·3a=6a
5.(2023山东青岛期末)随着全球科技的不断发展,一代又一代的科学家们研制出了很多性能优异的新型材料,其中微晶格金属是世界上最轻的金属和最轻的结构材料之一,密度低至0.000 9克/立方厘米.将数据0.000 9用科学记数法表示为 ( )
C.0.9×10 D .9×10
6.(2024安徽蚌埠蚌山月考)已知aA. a-1-2b
C.2a+1<2b+1
7.(2024安徽黄山期中)如图,下列条件中,不能判定AD∥BC的是 ( )
A.∠1=∠B B.∠2=∠5
C.∠3=∠4 D.∠DAB+∠B=180°
8.已知 则下列式子正确的是 ( )
A. x+y=2 B. x-y=2
C. xy=2 D. xy=-2
9.若关于x的一元一次不等式组 有3个整数解,则m的取值范围是 ( )
A.0≤m<1 B.0C.-4≤m<-3 D.010.(2024安徽合肥五十中期中)如图所示,以长方形ABCD的各边为直径向外作半圆得到一个新的图形,且新图形的周长为16π,同时此图形中四个半圆面积之和为44π,则长方形ABCD的面积为 ( )
A.10 B.20 C.40 D.80
二、填空题(每小题4分,共16分)
11.(2024安徽合肥二模)因式分解:
12.(2024 北京中考)方程 的解为
13.情境题·数学文化“直田七亩半,忘了长和短.记得立契时,长阔争一半.今问俊明公,此法如何算.”意思是:有一块面积为7亩半的长方形田地,忘了长与宽各是多少.只记得在立契约的时候说过,宽是长的一半.现在请你帮他算出田地的长是 步.(一亩=240平方步)
14.某同学设计了一个运算程序,如图,输入数m,每次运算结果是否大于n作为一次运算,若大于n,则输出结果;若小于或等于n,则将计算结果赋给m,重新运算.
(1)若m=5,n=20,则最终输出的结果为 ;
(2)若n=152,程序运算了3 次后停止,则 m可取的最小整数为 .
三、解答题(共74分)
15.(6分)计算:
16.(6分)解不等式: 并把它的解集在数轴上表示出来.
17.(6分)先化简: 再从-1,2,3中选一个合适的数作为 m的值代入求值.
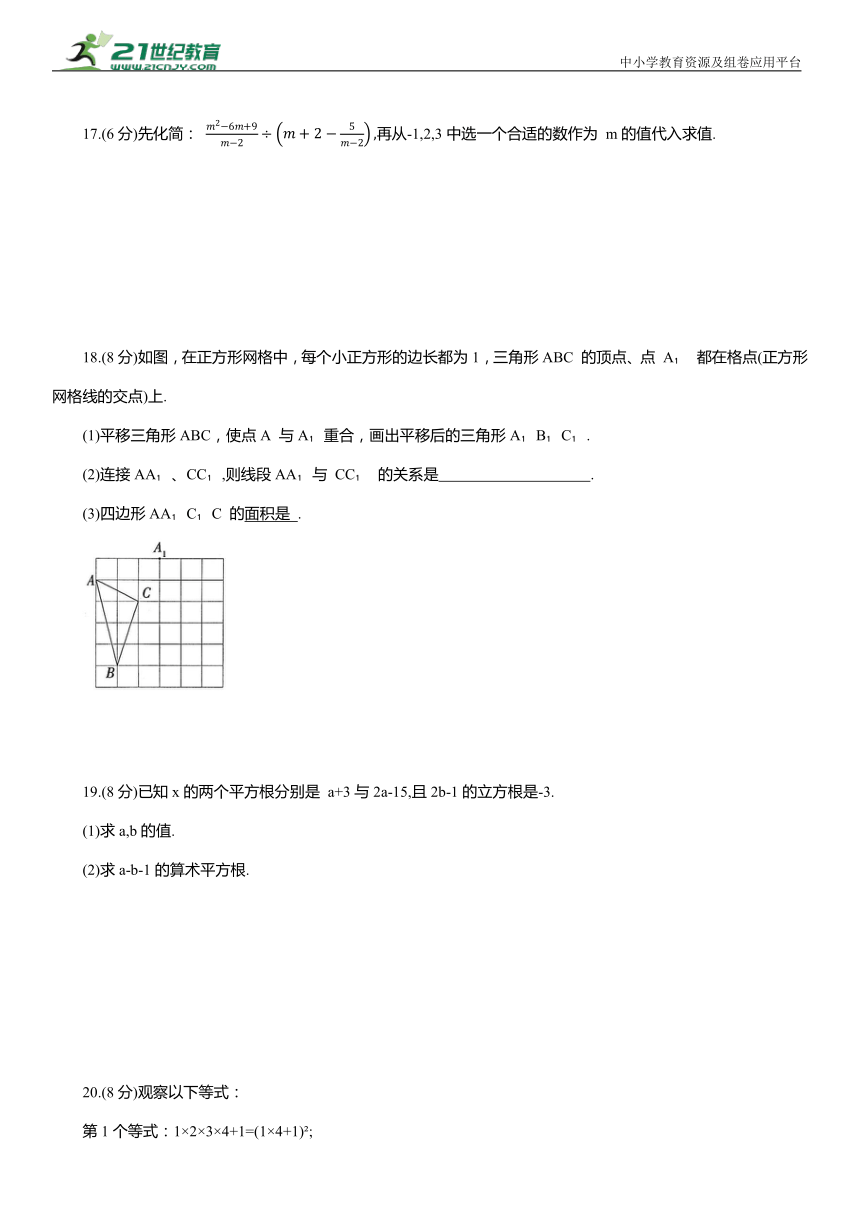
18.(8分)如图,在正方形网格中,每个小正方形的边长都为1,三角形ABC 的顶点、点 A 都在格点(正方形网格线的交点)上.
(1)平移三角形ABC,使点A 与A 重合,画出平移后的三角形A B C .
(2)连接AA 、CC ,则线段AA 与 CC 的关系是 .
(3)四边形AA C C 的面积是 .
19.(8分)已知x的两个平方根分别是 a+3与2a-15,且2b-1的立方根是-3.
(1)求a,b的值.
(2)求a-b-1的算术平方根.
20.(8分)观察以下等式:
第1个等式:1×2×3×4+1=(1×4+1) ;
第2个等式:2×3×4×5+1=(2×5+1) ;
第3个等式:3×4×5×6+1=(3×6+1) ;
第4个等式:4×5×6×7+1=(4×7+1) ;
……
按照以上规律,解决下列问题.
(1)写出第6个等式: .
(2)写出第n个等式(n为正整数),并证明.
21.(10分)某商场准备购进甲、乙两种商品进行销售,若每个甲种商品的进价比每个乙种商品的进价少2元,且用80元购进甲种商品的数量与用100 元购进乙种商品的数量相同.
(1)求甲、乙两种商品每个的进价分别是多少元.
(2)若该商场购进甲种商品的数量比乙种商品的数量的3倍少 5个,且购进甲、乙两种商品的总数量不超过95个,则商场最多购进乙种商品多少个
中小学教育资源及组卷应用平台
(3)在(2)的条件下,如果甲、乙两种商品的售价分别是 12 元/个和15 元/个,且将购进的甲、乙两种商品全部售出后,可使销售两种商品的总利润超过380元,那么该商场购进甲、乙两种商品有哪几种方案
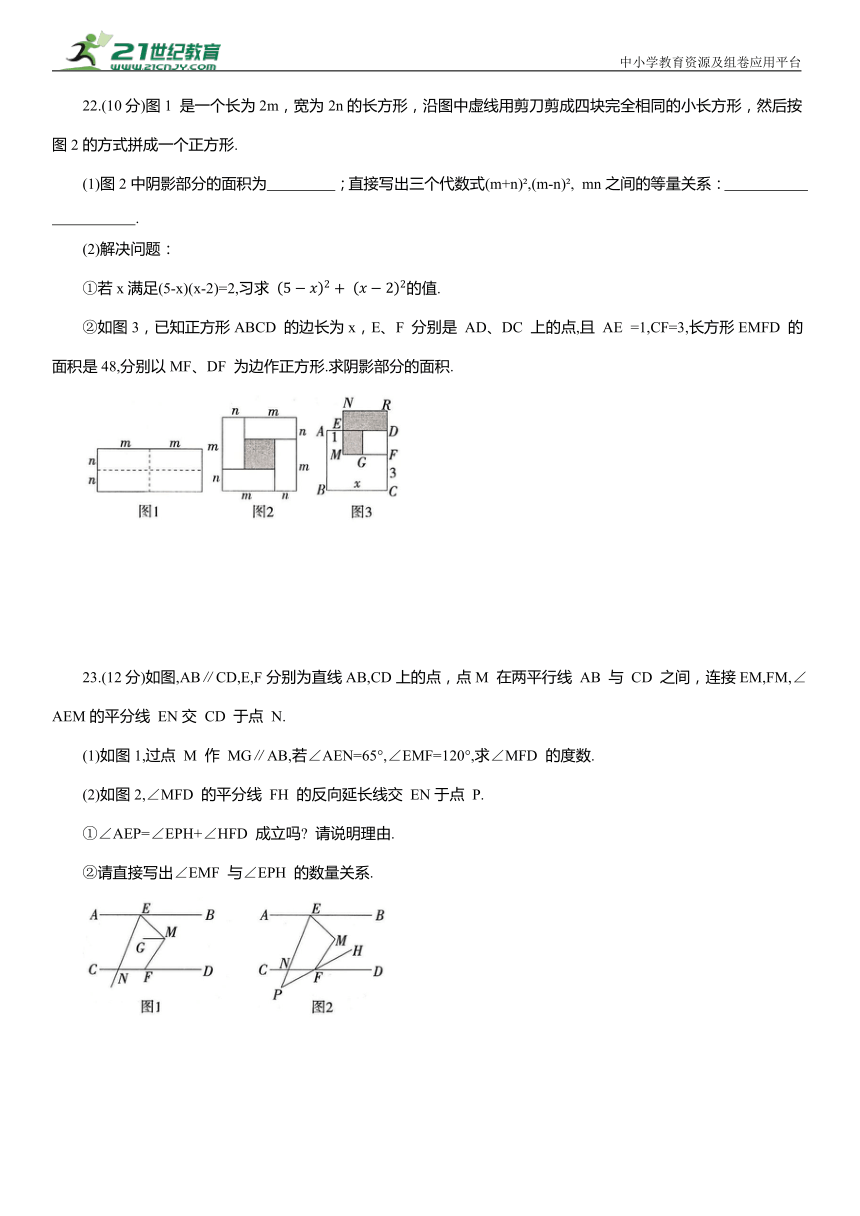
22.(10分)图1 是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪成四块完全相同的小长方形,然后按图2的方式拼成一个正方形.
(1)图2中阴影部分的面积为 ;直接写出三个代数式(m+n) ,(m-n) , mn之间的等量关系: .
(2)解决问题:
①若x满足(5-x)(x-2)=2,习求 的值.
②如图3,已知正方形ABCD 的边长为x,E、F 分别是 AD、DC 上的点,且 AE =1,CF=3,长方形EMFD 的面积是48,分别以MF、DF 为边作正方形.求阴影部分的面积.
23.(12分)如图,AB∥CD,E,F分别为直线AB,CD上的点,点M 在两平行线 AB 与 CD 之间,连接EM,FM,∠AEM的平分线 EN交 CD 于点 N.
(1)如图1,过点 M 作 MG∥AB,若∠AEN=65°,∠EMF=120°,求∠MFD 的度数.
(2)如图2,∠MFD 的平分线 FH 的反向延长线交 EN于点 P.
①∠AEP=∠EPH+∠HFD 成立吗 请说明理由.
②请直接写出∠EMF 与∠EPH 的数量关系.
①C-2, ,0是有理数, 是无理数.
②A 根据分式有意义的条件,得x+1≠0,解得x≠-1.
③B选项A、C、D中的图形都是由一个基础图形通过旋转得到的,选项B中的图形是由一个基础图形通过平移得到的.故选 B.
故选项 A、B、D错误,选项 C正确.故选 C.
5A 0.0009=9×10 .
6D a-2b,故选项B中式子成立;a⑦C因为∠1=∠B,所以AD∥BC(同位角相等,两直线平行),故选项A不符合题意;因为∠2=∠5,所以AD∥BC(内错角相等,两直线平行),故选项 B不符合题意;因为∠3=∠4,所以AB∥CD(内错角相等,两直线平行),不能判定AD∥BC,故选项 C符合题意;因为∠DAB+∠B=180°,所以AD∥BC(同旁内角互补,两直线平行),故选项D不符合题意.
⑧D由x+y+z=0,得z=-x-y,将z=-x-y代入. =4,得 化简,得-2xy=4,即 xy=-2.故选 D.
9A 由x-m>0,得x>m,由2x-4≤2,得x≤3,因为不等式组有解,所以不等式组的解集为m10 C设AB=a,BC=b,根据题意,得πa+πb=16π,π× 所以 因为 所以256=176+2ab,解得 ab=40,所以
11答案
解析 原式
答案 x=-1
解析 去分母,得x+(2x+3)=0,解得x=-1,经检验,x=-1是原分式方程的解.
答案 60
解析 设此长方形田地的宽为x步,则长为2x步,根据题意,得x·2x=240×7.5,所以x=30(负值舍去),则2x=60,所以田地的长为60步.
答案 (1)77 (2)4
解析 (1)当m=5时,5m-8=5×5-8=17<20;当m=17时,5m-8=5×17-8=77>20,故最终输出的结果为77.
(2) 根据 题 意, 列 不 等 式 组, 得 解得 故 m可取的最小整数为4.
解析 原式=-1×4+9+1·
解析 去分母,得x-3-2x≥-4,
移项、合并同类项,得-x≥-1,..…… 2分
系数化为1,得x≤1, …………………………… 4分
将不等式的解集在数轴上表示如图:……………6分
17 解析 原式
2分
4分
由题意知m≠2,m≠±3,所以取m=-1,
当m=-1时,原式 6分
解析 (1)如图,三角形A B C 即为所求. …… 2分
且AA ∥CC . … 5分
(3)四边形AA C C的面积 ……………………………………… 8 分
解析 (1)因为x的平方根分别是a+3与2a-15,
所以a+3+2a-15=0,解得a=4. 2分
因为2b-1的立方根是-3,
所以2b-1=-27,解得b=-13.…………………… 4分
(2)因为a=4,b=-13,
所以a-b-1=4+13-1=16, ……………………… 6分
16的算术平方根是4,
所以a-b-1的算术平方根是4. 8分
解析 (1)6×7×8×9+1=(6×9+1) . 3分
(2)第n个等式为n(n+1)(n+2)(n+3)+1= …………………………………… 5分
证明:左边=n(n+1)(n+2)(n+3)+1
=n(n+3)·(n+1)(n+2)+1
右边,所以等式成立. 8分
解析 (1)设每个乙种商品的进价为x元,则每个甲种商品的进价为(x-2)元,
根据题意,得 解得x=10,
经检验,x=10是原方程的根,且符合题意,……2分所以x-2=10-2=8.
答:每个甲种商品的进价为8元,每个乙种商品的进价为10元. 3分
(2)设购进乙种商品y个,则购进甲种商品(3y-5)个.
根据题意,得3y-5+y≤95,解得y≤25. ……………………………………… 5分
答:商场最多购进乙种商品25个. 6分
(3)由题意得,(12-8)(3y-5)+(15-10)y>380,解得 …………………………………… 8分
因为y为整数,且y≤25,
所以y=24或25.
当y=24时,3y-5=67;
当y=25时,3y-5=70.
所以共有两种方案,如下:
方案一:购进甲种商品67个,乙种商品24个;
方案二:购进甲种商品70个,乙种商品25个.…………………………………………………… 10分
解析 ……2分
(2)①因为(5-x)+(x-2)=3,…………………… 3分
所以
所以 的值为5. 6分
②由题意知,MF=x-1,DF=x-3,S长方形EMFD=MF·DF
=(x-1)(x-3)=48,
所以MF-DF=(x-1)-(x-3)=2,
令x-1=a,x-3=b,则.ab=48,a-b=2,
因为
所以
所以a+b=14,
所以
28. 10分
②解析 (1)因为 EN平分∠AEM,∠AEN=65°,
所以∠AEM=2∠AEN=130°,
所以
因为MG∥AB,所以∠EMG=∠BEM=50°.
因为∠EMF=120°,所以
因为MG∥AB,AB∥CD,所以MG∥CD,
所以∠MFD=∠GMF=70°. 4分
(2)①成立. 5分
理由:过点 P作PQ∥CD,如图所示,
因为AB∥CD,所以AB∥PQ∥CD,
所以∠HFD=∠HPQ,∠AEP=∠EPQ…………… 6分
因为∠EPQ=∠EPH+∠HPQ=∠EPH+∠HFD,
所以∠AEP=∠EPH+∠HFD. …………………… 8分
②∠EMF=180°-2∠EPH. 12分
详解:如图,过点M作MK∥AB,
因为AB∥CD,所以CD∥MK∥AB,
所以∠BEM=∠EMK,∠KMF=∠MFD,
所以∠EMF=∠BEM+∠MFD.
因为EN平分∠AEM,FH平分∠MFD,
所以∠AEN=∠MEN,∠MFH=∠HFD.
设∠AEN=∠MEN=y,∠MFH=∠HFD=∠PFN=x,
则∠BEM=180°-2y,∠MFD=2x,
所以∠EMF=180°-2y+2x,
根据①可知∠EPH=∠AEN-∠HFD=y-x,
所以∠EMF=180°-2y+2x=180°-2(y-x)= 180°-2∠EPH,
即∠EMF=180°-2∠EPH.
一、选择题(每小题3分,共30分)
1.(2024 四川遂宁中考)下列各数中,无理数是( )
A.-2 B. C . D.0
2.(2024安徽马鞍山和县期末)使分式 有意义的x的取值范围为 ( )
A. x≠-1 B. x≠1
C. x≠2 D. x≠-1且x≠2
3.(2024安徽池州贵池期末)下列图形中可以由一个基础图形通过平移变换得到的是 ( )
4.(2024吉林长春中考)下列运算一定正确的是( )
A.2a·3a=6a
5.(2023山东青岛期末)随着全球科技的不断发展,一代又一代的科学家们研制出了很多性能优异的新型材料,其中微晶格金属是世界上最轻的金属和最轻的结构材料之一,密度低至0.000 9克/立方厘米.将数据0.000 9用科学记数法表示为 ( )
C.0.9×10 D .9×10
6.(2024安徽蚌埠蚌山月考)已知a
C.2a+1<2b+1
7.(2024安徽黄山期中)如图,下列条件中,不能判定AD∥BC的是 ( )
A.∠1=∠B B.∠2=∠5
C.∠3=∠4 D.∠DAB+∠B=180°
8.已知 则下列式子正确的是 ( )
A. x+y=2 B. x-y=2
C. xy=2 D. xy=-2
9.若关于x的一元一次不等式组 有3个整数解,则m的取值范围是 ( )
A.0≤m<1 B.0
A.10 B.20 C.40 D.80
二、填空题(每小题4分,共16分)
11.(2024安徽合肥二模)因式分解:
12.(2024 北京中考)方程 的解为
13.情境题·数学文化“直田七亩半,忘了长和短.记得立契时,长阔争一半.今问俊明公,此法如何算.”意思是:有一块面积为7亩半的长方形田地,忘了长与宽各是多少.只记得在立契约的时候说过,宽是长的一半.现在请你帮他算出田地的长是 步.(一亩=240平方步)
14.某同学设计了一个运算程序,如图,输入数m,每次运算结果是否大于n作为一次运算,若大于n,则输出结果;若小于或等于n,则将计算结果赋给m,重新运算.
(1)若m=5,n=20,则最终输出的结果为 ;
(2)若n=152,程序运算了3 次后停止,则 m可取的最小整数为 .
三、解答题(共74分)
15.(6分)计算:
16.(6分)解不等式: 并把它的解集在数轴上表示出来.
17.(6分)先化简: 再从-1,2,3中选一个合适的数作为 m的值代入求值.
18.(8分)如图,在正方形网格中,每个小正方形的边长都为1,三角形ABC 的顶点、点 A 都在格点(正方形网格线的交点)上.
(1)平移三角形ABC,使点A 与A 重合,画出平移后的三角形A B C .
(2)连接AA 、CC ,则线段AA 与 CC 的关系是 .
(3)四边形AA C C 的面积是 .
19.(8分)已知x的两个平方根分别是 a+3与2a-15,且2b-1的立方根是-3.
(1)求a,b的值.
(2)求a-b-1的算术平方根.
20.(8分)观察以下等式:
第1个等式:1×2×3×4+1=(1×4+1) ;
第2个等式:2×3×4×5+1=(2×5+1) ;
第3个等式:3×4×5×6+1=(3×6+1) ;
第4个等式:4×5×6×7+1=(4×7+1) ;
……
按照以上规律,解决下列问题.
(1)写出第6个等式: .
(2)写出第n个等式(n为正整数),并证明.
21.(10分)某商场准备购进甲、乙两种商品进行销售,若每个甲种商品的进价比每个乙种商品的进价少2元,且用80元购进甲种商品的数量与用100 元购进乙种商品的数量相同.
(1)求甲、乙两种商品每个的进价分别是多少元.
(2)若该商场购进甲种商品的数量比乙种商品的数量的3倍少 5个,且购进甲、乙两种商品的总数量不超过95个,则商场最多购进乙种商品多少个
中小学教育资源及组卷应用平台
(3)在(2)的条件下,如果甲、乙两种商品的售价分别是 12 元/个和15 元/个,且将购进的甲、乙两种商品全部售出后,可使销售两种商品的总利润超过380元,那么该商场购进甲、乙两种商品有哪几种方案
22.(10分)图1 是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀剪成四块完全相同的小长方形,然后按图2的方式拼成一个正方形.
(1)图2中阴影部分的面积为 ;直接写出三个代数式(m+n) ,(m-n) , mn之间的等量关系: .
(2)解决问题:
①若x满足(5-x)(x-2)=2,习求 的值.
②如图3,已知正方形ABCD 的边长为x,E、F 分别是 AD、DC 上的点,且 AE =1,CF=3,长方形EMFD 的面积是48,分别以MF、DF 为边作正方形.求阴影部分的面积.
23.(12分)如图,AB∥CD,E,F分别为直线AB,CD上的点,点M 在两平行线 AB 与 CD 之间,连接EM,FM,∠AEM的平分线 EN交 CD 于点 N.
(1)如图1,过点 M 作 MG∥AB,若∠AEN=65°,∠EMF=120°,求∠MFD 的度数.
(2)如图2,∠MFD 的平分线 FH 的反向延长线交 EN于点 P.
①∠AEP=∠EPH+∠HFD 成立吗 请说明理由.
②请直接写出∠EMF 与∠EPH 的数量关系.
①C-2, ,0是有理数, 是无理数.
②A 根据分式有意义的条件,得x+1≠0,解得x≠-1.
③B选项A、C、D中的图形都是由一个基础图形通过旋转得到的,选项B中的图形是由一个基础图形通过平移得到的.故选 B.
故选项 A、B、D错误,选项 C正确.故选 C.
5A 0.0009=9×10 .
6D a
⑧D由x+y+z=0,得z=-x-y,将z=-x-y代入. =4,得 化简,得-2xy=4,即 xy=-2.故选 D.
9A 由x-m>0,得x>m,由2x-4≤2,得x≤3,因为不等式组有解,所以不等式组的解集为m
11答案
解析 原式
答案 x=-1
解析 去分母,得x+(2x+3)=0,解得x=-1,经检验,x=-1是原分式方程的解.
答案 60
解析 设此长方形田地的宽为x步,则长为2x步,根据题意,得x·2x=240×7.5,所以x=30(负值舍去),则2x=60,所以田地的长为60步.
答案 (1)77 (2)4
解析 (1)当m=5时,5m-8=5×5-8=17<20;当m=17时,5m-8=5×17-8=77>20,故最终输出的结果为77.
(2) 根据 题 意, 列 不 等 式 组, 得 解得 故 m可取的最小整数为4.
解析 原式=-1×4+9+1·
解析 去分母,得x-3-2x≥-4,
移项、合并同类项,得-x≥-1,..…… 2分
系数化为1,得x≤1, …………………………… 4分
将不等式的解集在数轴上表示如图:……………6分
17 解析 原式
2分
4分
由题意知m≠2,m≠±3,所以取m=-1,
当m=-1时,原式 6分
解析 (1)如图,三角形A B C 即为所求. …… 2分
且AA ∥CC . … 5分
(3)四边形AA C C的面积 ……………………………………… 8 分
解析 (1)因为x的平方根分别是a+3与2a-15,
所以a+3+2a-15=0,解得a=4. 2分
因为2b-1的立方根是-3,
所以2b-1=-27,解得b=-13.…………………… 4分
(2)因为a=4,b=-13,
所以a-b-1=4+13-1=16, ……………………… 6分
16的算术平方根是4,
所以a-b-1的算术平方根是4. 8分
解析 (1)6×7×8×9+1=(6×9+1) . 3分
(2)第n个等式为n(n+1)(n+2)(n+3)+1= …………………………………… 5分
证明:左边=n(n+1)(n+2)(n+3)+1
=n(n+3)·(n+1)(n+2)+1
右边,所以等式成立. 8分
解析 (1)设每个乙种商品的进价为x元,则每个甲种商品的进价为(x-2)元,
根据题意,得 解得x=10,
经检验,x=10是原方程的根,且符合题意,……2分所以x-2=10-2=8.
答:每个甲种商品的进价为8元,每个乙种商品的进价为10元. 3分
(2)设购进乙种商品y个,则购进甲种商品(3y-5)个.
根据题意,得3y-5+y≤95,解得y≤25. ……………………………………… 5分
答:商场最多购进乙种商品25个. 6分
(3)由题意得,(12-8)(3y-5)+(15-10)y>380,解得 …………………………………… 8分
因为y为整数,且y≤25,
所以y=24或25.
当y=24时,3y-5=67;
当y=25时,3y-5=70.
所以共有两种方案,如下:
方案一:购进甲种商品67个,乙种商品24个;
方案二:购进甲种商品70个,乙种商品25个.…………………………………………………… 10分
解析 ……2分
(2)①因为(5-x)+(x-2)=3,…………………… 3分
所以
所以 的值为5. 6分
②由题意知,MF=x-1,DF=x-3,S长方形EMFD=MF·DF
=(x-1)(x-3)=48,
所以MF-DF=(x-1)-(x-3)=2,
令x-1=a,x-3=b,则.ab=48,a-b=2,
因为
所以
所以a+b=14,
所以
28. 10分
②解析 (1)因为 EN平分∠AEM,∠AEN=65°,
所以∠AEM=2∠AEN=130°,
所以
因为MG∥AB,所以∠EMG=∠BEM=50°.
因为∠EMF=120°,所以
因为MG∥AB,AB∥CD,所以MG∥CD,
所以∠MFD=∠GMF=70°. 4分
(2)①成立. 5分
理由:过点 P作PQ∥CD,如图所示,
因为AB∥CD,所以AB∥PQ∥CD,
所以∠HFD=∠HPQ,∠AEP=∠EPQ…………… 6分
因为∠EPQ=∠EPH+∠HPQ=∠EPH+∠HFD,
所以∠AEP=∠EPH+∠HFD. …………………… 8分
②∠EMF=180°-2∠EPH. 12分
详解:如图,过点M作MK∥AB,
因为AB∥CD,所以CD∥MK∥AB,
所以∠BEM=∠EMK,∠KMF=∠MFD,
所以∠EMF=∠BEM+∠MFD.
因为EN平分∠AEM,FH平分∠MFD,
所以∠AEN=∠MEN,∠MFH=∠HFD.
设∠AEN=∠MEN=y,∠MFH=∠HFD=∠PFN=x,
则∠BEM=180°-2y,∠MFD=2x,
所以∠EMF=180°-2y+2x,
根据①可知∠EPH=∠AEN-∠HFD=y-x,
所以∠EMF=180°-2y+2x=180°-2(y-x)= 180°-2∠EPH,
即∠EMF=180°-2∠EPH.
同课章节目录
