期末素养综合测试 (二) (含答案)2024-2025学年沪科版七年级数学下册
文档属性
| 名称 | 期末素养综合测试 (二) (含答案)2024-2025学年沪科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 215.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:07:31 | ||
图片预览



文档简介
期末素养综合测试 (二)
一、选择题(每小题3分,共30分)
1.在实数 ,0, ,π, 中,无理数的个数是 ( )
A.1 B.2 C.3 D.4
2.(2024安徽安庆期中)下列各式中,正确的是( )
3.(2024安徽滁州期末)生物学家发现某种花粉的直径约为0.000 002 1 毫米,数据0.000 002 1用科学记数法表示正确的是 ( )
4.(2024江苏苏州期中)对于分式 下列说法错误的是 ( )
A.当x≠3时,分式有意义
B.当x=3时,分式的值为0
C.当x=1时,分式的值为-1
D.分式的值不可能为2
5.(2024安徽合肥蜀山期末)已知aB. a+cC.-3a>-3b
6.(2024 新疆中考)某校九年级学生去距学校20km的科技馆研学,一部分学生乘甲车先出发,5min 后其余学生几何画板演示再乘乙车出发,结果同时到达.已知乙车的速度是甲车速度的1.2倍,设甲车的速度为 xkm/h,根据题意可列方程为 ( )
7.有一个数值转换器,原理如图所示,当输入x的值为16 时,输出的y的值为 ( )
A.4 C.2 D.1
8.(2024安徽安庆期中)若关于x 的一元一次不等式组 有解,则a的取值范围是( )
A. a≥4 B. a>4 C. a≤4 D. a<4
9.(2024安徽合肥庐江期中)如图,下列判断中错误的是 ( )
A.因为AB∥CD,所以∠BAC=∠ACD
B.因为∠BAD+∠ADC=180°,所以AB∥CD
C.因为AD∥BC,所以∠BCA=∠DAC
D.因为∠ABD=∠CDB,所以AD∥BC
10. 已知a、b、c均不为0,且 则 的值是( )
B.
二、填空题(每小题4分,共16分)
11.(2024 安徽合肥蜀山一模)因式分解:
12.(2024安徽合肥蜀山期中)写出一个大于3 且小于4的无理数: .
13.(2024安徽蚌埠蚌山期末)如图,直线 AB、CD 相交于点O,OD平分∠BOF,OE⊥CD于点O,则∠EOB∶ ∠AOF= .
14.(2024安徽芜湖期中)已知AB∥CD,请回答以下问题:
(1)如图1,∠1、∠2、∠3、∠4、∠5之间的数量关系是 ;
(2)如图2,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM= .
三、解答题(共74分)
15.(6分)计算:
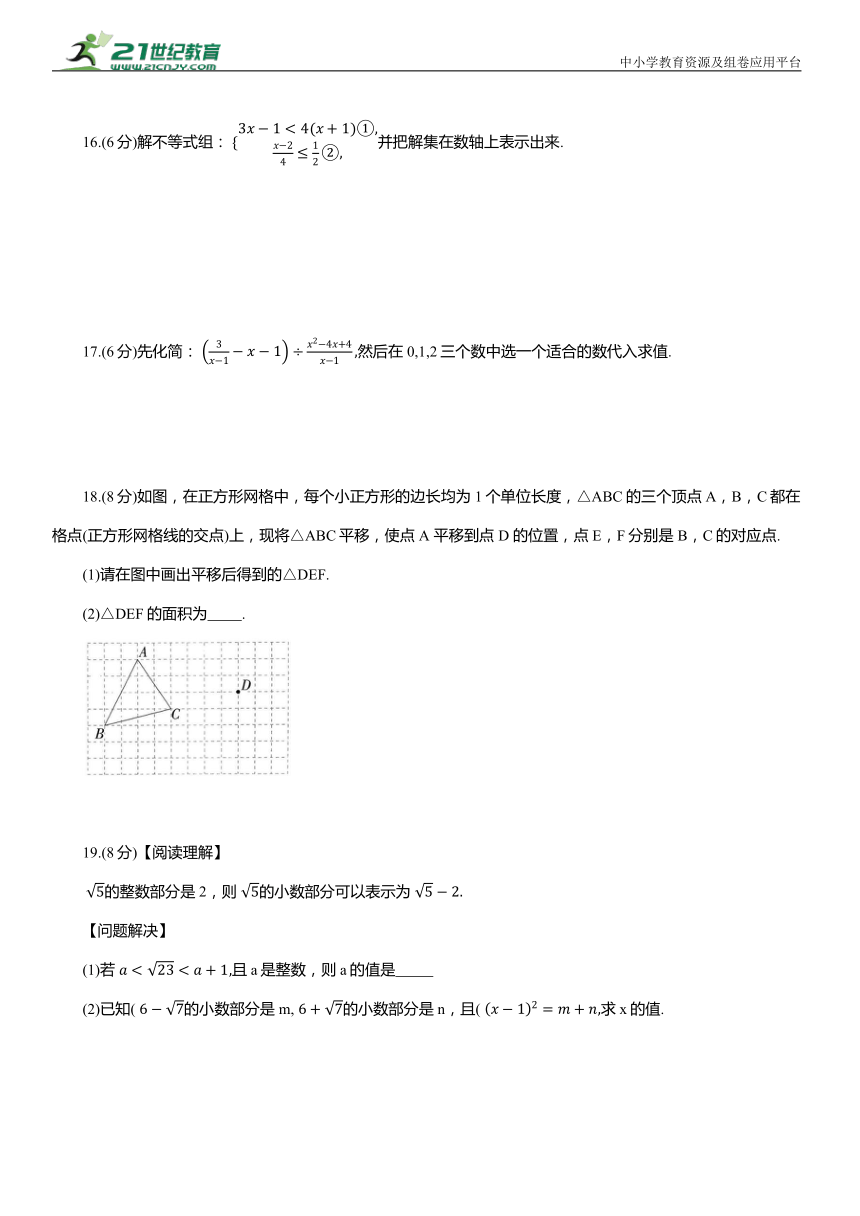
16.(6分)解不等式组: 并把解集在数轴上表示出来.
17.(6分)先化简: 然后在0,1,2三个数中选一个适合的数代入求值.
18.(8分)如图,在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格线的交点)上,现将△ABC平移,使点 A 平移到点 D 的位置,点E,F分别是B,C的对应点.
(1)请在图中画出平移后得到的△DEF.
(2)△DEF的面积为 .
19.(8分)【阅读理解】
的整数部分是2,则 的小数部分可以表示为
【问题解决】
(1)若 且a是整数,则a的值是
(2)已知( 的小数部分是m, 的小数部分是n,且( 求x的值.
20.(8分)观察以下等式:
第1个等式:1×(2+4)+4×2=2×5+4;
第2个等式:2×(6+4)+4×5=3×8+16;
第3个等式:3×(12+4)+4×10=4×13+36;
第4个等式:4×(20+4)+4×17=5×20+64;
……
按照以上规律,解决下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式(n为正整数),并证明.
21.(10分)为加快公共领域充电基础设施建设,规范居民安全用电行为,某市计划新建一批智能充电桩.经调研,市场上有A 型、B型两种充电桩,已知A 型充电桩的单价比 B 型充电桩的单价少0.2万元,用12 万元购买A 型充电桩的数量与用16万元购买B型充电桩的数量相等.
(1)求A 型、B型充电桩的单价各是多少.
中小学教育资源及组卷应用平台
(2)该市决定购买A型、B型充电桩共300个,且花费不超过200万元,则至少购买A 型充电桩多少个
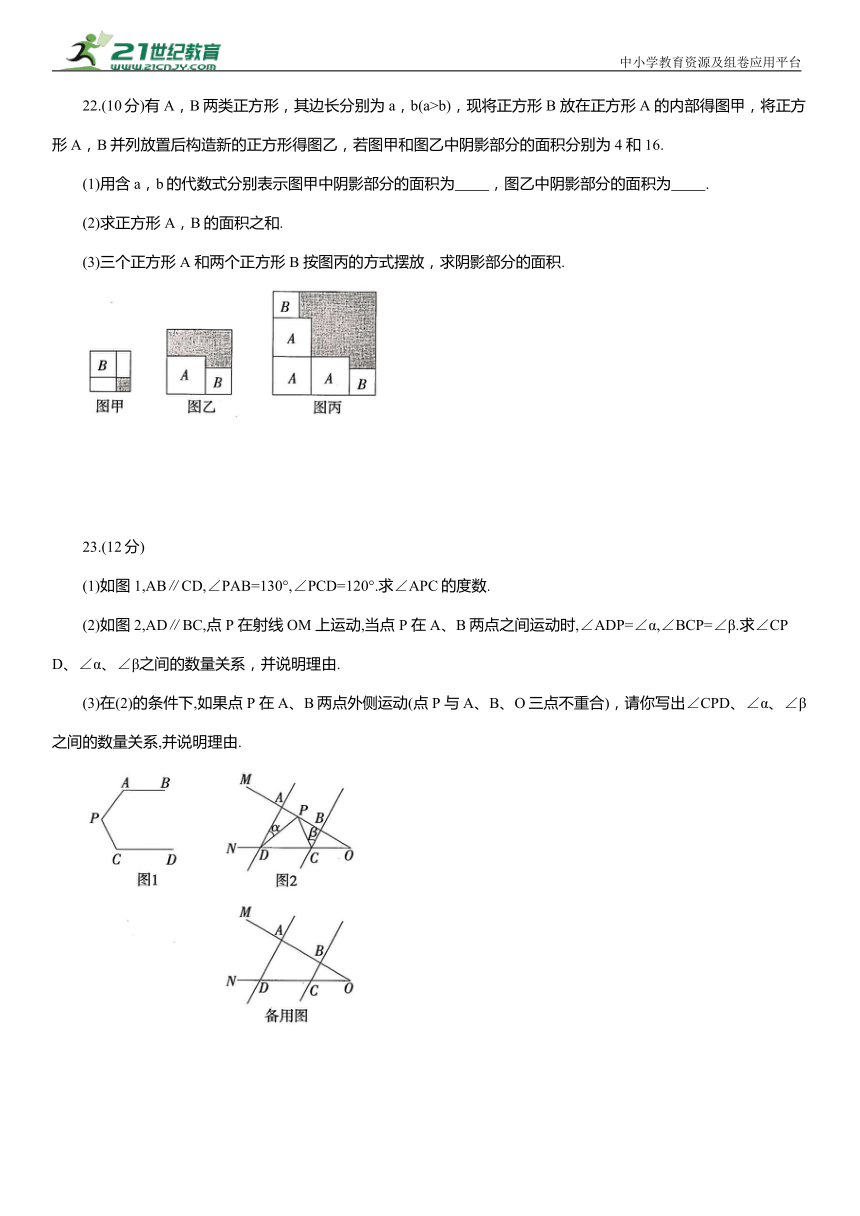
22.(10分)有A,B两类正方形,其边长分别为a,b(a>b),现将正方形 B 放在正方形A 的内部得图甲,将正方形A,B并列放置后构造新的正方形得图乙,若图甲和图乙中阴影部分的面积分别为4 和16.
(1)用含a,b的代数式分别表示图甲中阴影部分的面积为 ,图乙中阴影部分的面积为 .
(2)求正方形A,B的面积之和.
(3)三个正方形 A 和两个正方形 B 按图丙的方式摆放,求阴影部分的面积.
23.(12分)
(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
(2)如图2,AD∥BC,点 P 在射线 OM 上运动,当点 P 在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.求∠CPD、∠α、∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点 P 在A、B两点外侧运动(点P 与A、B、O三点不重合),请你写出∠CPD、∠α、∠β之间的数量关系,并说明理由.
①B 0, 和- 是有理数, 和π是无理数,故无理数共有2个.
故选项A正确; 故选项B错误;a 与a 不是同类项,不能合并,故选项C错误; 故选项D错误.
③A 0.000 002 1=2.1×10 .
④B 当x≠3时,x-3≠0,分式有意义,故选项A不符合题意;当x=3时,分式的分母为0,分式无意义,故选项B符合题意;当x=1时,分式的值为 故选项C不符合题意;若 则x的值不存在,所以分式的值不可能为2,故选项D不符合题意.
⑤D因为a0时, 当 时, 故选项 D 符合题意.故选D.
6D 甲车的速度为 xkm/h,则乙车的速度为1.2x km/h,根据一部分学生乘甲车先出发,5min后其余学生再
乘乙车出发,结果同时到达,可列分式方程为 即
⑦B当输入x的值为16时,取算术平方根是4,4是有理数,再次输入,4的算术平方根是2,2是有理数,再次输入,2的算术平方根是 , 是无理数,所以输出的y的值是
8D 不等式组
解不等式①,得x≥2,解不等式②,得 因为关于x的一元一次不等式组 有解,所以 解得a<4.
9D 因为AB∥CD,所以∠BAC=∠ACD(两直线平行,内错角相等),故选项 A不符合题意;因为∠BAD+∠ADC=180°,所以AB∥CD(同旁内角互补,两直线平行),故选项 B不符合题意;因为AD∥BC,所以∠BCA=∠DAC(两直线平行,内错角相等),故选项C不符合题意;因为∠ABD=∠CDB,所以AB∥CD,无法得出AD∥BC,故选项D符合题意.
10 A 将三个等式左右两边分别相加,得 即 的倒数= 所以
答案 4(x+5)(x-5)
解析 原式
答案 π(答案不唯一)
答案 1:2
解析 因为OD平分∠BOF,所以 因为OE⊥CD,所以∠EOD=90°,所以∠EOB=90°- 因为∠AOF = 180°-∠BOF,所以∠EOB : ∠AOF =
答案 (1)∠2+∠4=∠1+∠3+∠5 (2)40°
解析 (1)如图1,作GM∥AB,FN∥AB,EH∥AB.因为AB∥CD,所以AB∥GM∥FN∥EH∥CD,所以∠1=∠AEH,∠HEG=∠EGM,∠MGF=∠GFN,∠NFC=∠5,所以∠AEG+∠GFC=∠1+∠EGF+∠5,即∠2+∠4=∠1+∠3+∠5.
(2)如图2,作KG∥AB,HQ∥AB,MN与HQ 交于点T.因为 AB∥CD,所以 AB∥KG∥HQ∥CD,所以∠FGK=∠EFA=30°,∠HTN = ∠CNP = 50°.因为∠FGH=90°,所以∠KGH=60°,所以∠GHQ=∠KGH=60°.易知∠HTN=∠QHM+∠M,因为∠M=30°,所以∠QHM=20°,所以∠GHM=∠GHQ-∠QHM=40°.
解析 原式=-9-4+1-2 ………………………… 3分
=-14. 6分
解析 解不等式①,得x>-5,
解不等式②,得x≤4, …………………………… 2分
故原不等式组的解集是-5将不等式组的解集在数轴上表示如图: 6分
解析 原式
……… 4分
因为x-1≠0且2-x≠0,所以x≠1且x≠2,
所以x=0,则原式=1. 6分
解析 (1)如图所示: 4分
(2)7. 8分
详解: 2-3-4=7.
解析 (1)4. 3分
详解:因为16<23<25,所以 所以
因为 且a是整数,所以a=4.
(2)因为4<7<9,所以 所以 所以 …………………… 4 分
因为 的小数部分是m, 的小数部分是n,
所以
6分
因为
所以
所以x-1=1或x-1=-1,
则x=2或x=0. 8分
解析(1)5×(30+4)+4×26=6×29+100. …… 2分
4分
证明:左边
右边
因为左边=右边,
所以等式成立. 8分
解析 (1)设A型充电桩的单价为x万元,则B型充电桩的单价为(x+0.2)万元.
根据题意,得 ………………… 2分解得x=0.6, ……………………………………… 3分
经检验,x=0.6是所列方程的解,且符合题意,所以x+0.2=0.6+0.2=0.8.
答:A型充电桩的单价为0.6万元,B型充电桩的单价为0.8万元. 5分
(2)设购买A 型充电桩m个,则购买B 型充电桩(300-m)个,
根据题意,得0.6m+0.8(300-m)≤200, 8分解得 m≥200,所以m的最小值为200.
答:至少购买A 型充电桩200个. 10分
解析 (1)(a-b) ;2ab. …… 2分
(2)根据题意,得 所以 所以正方形A,B的面积之和为20.……… 6分
(3)由(2)知(
所以ab=8,a-b=2,
所以(
因为a+b>0,所以a+b=6,
所以题图丙中阴影部分的面积为
=a -b +4ab=(a+b)(a-b)+4ab=6×2+4×8=44.…10分
②解析 (1)如图,过点 P作PH∥AB,
则∠BAP+∠APH=180°,所以∠APH=180°-∠BAP=180°-130°=50°. ……
…………………………… … 2分
因为AB∥CD,PH∥AB,所以CD∥PH,所以∠PCD+∠HPC=180°,所以 所以∠APC=∠HPC+∠APH=60°+50°=110°. ……4分
(2)如图,过点P作PF∥AD.
所以∠ADP=∠DPF,即∠α=∠DPF.
因为PF∥AD,AD∥BC,所以PF∥BC,
所以∠FPC=∠PCB,即∠FPC=∠β,
所以∠CPD=∠DPF+∠FPC=∠α+∠β,
即∠CPD=∠α+∠β.……………………………… 8分
(3)当P在A的左侧时,如图:
设PC交AD于点K,因为AD∥BC,
所以∠DKC=∠BCP=∠β.
易知∠DKC=∠CPD+∠ADP,
因为∠ADP=∠α,所以∠β=∠CPD+∠α,
所以∠CPD=∠β-∠α. 10分
当P在B的右侧时,如图:
设PD交BC于点Q,因为AD∥BC,
所以∠ADP=∠DQC=∠α.
易知∠DQC=∠CPD+∠BCP,
所以∠α=∠CPD+∠β,
所以∠CPD=∠α-∠β. 12分
一、选择题(每小题3分,共30分)
1.在实数 ,0, ,π, 中,无理数的个数是 ( )
A.1 B.2 C.3 D.4
2.(2024安徽安庆期中)下列各式中,正确的是( )
3.(2024安徽滁州期末)生物学家发现某种花粉的直径约为0.000 002 1 毫米,数据0.000 002 1用科学记数法表示正确的是 ( )
4.(2024江苏苏州期中)对于分式 下列说法错误的是 ( )
A.当x≠3时,分式有意义
B.当x=3时,分式的值为0
C.当x=1时,分式的值为-1
D.分式的值不可能为2
5.(2024安徽合肥蜀山期末)已知a
6.(2024 新疆中考)某校九年级学生去距学校20km的科技馆研学,一部分学生乘甲车先出发,5min 后其余学生几何画板演示再乘乙车出发,结果同时到达.已知乙车的速度是甲车速度的1.2倍,设甲车的速度为 xkm/h,根据题意可列方程为 ( )
7.有一个数值转换器,原理如图所示,当输入x的值为16 时,输出的y的值为 ( )
A.4 C.2 D.1
8.(2024安徽安庆期中)若关于x 的一元一次不等式组 有解,则a的取值范围是( )
A. a≥4 B. a>4 C. a≤4 D. a<4
9.(2024安徽合肥庐江期中)如图,下列判断中错误的是 ( )
A.因为AB∥CD,所以∠BAC=∠ACD
B.因为∠BAD+∠ADC=180°,所以AB∥CD
C.因为AD∥BC,所以∠BCA=∠DAC
D.因为∠ABD=∠CDB,所以AD∥BC
10. 已知a、b、c均不为0,且 则 的值是( )
B.
二、填空题(每小题4分,共16分)
11.(2024 安徽合肥蜀山一模)因式分解:
12.(2024安徽合肥蜀山期中)写出一个大于3 且小于4的无理数: .
13.(2024安徽蚌埠蚌山期末)如图,直线 AB、CD 相交于点O,OD平分∠BOF,OE⊥CD于点O,则∠EOB∶ ∠AOF= .
14.(2024安徽芜湖期中)已知AB∥CD,请回答以下问题:
(1)如图1,∠1、∠2、∠3、∠4、∠5之间的数量关系是 ;
(2)如图2,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM= .
三、解答题(共74分)
15.(6分)计算:
16.(6分)解不等式组: 并把解集在数轴上表示出来.
17.(6分)先化简: 然后在0,1,2三个数中选一个适合的数代入求值.
18.(8分)如图,在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点A,B,C都在格点(正方形网格线的交点)上,现将△ABC平移,使点 A 平移到点 D 的位置,点E,F分别是B,C的对应点.
(1)请在图中画出平移后得到的△DEF.
(2)△DEF的面积为 .
19.(8分)【阅读理解】
的整数部分是2,则 的小数部分可以表示为
【问题解决】
(1)若 且a是整数,则a的值是
(2)已知( 的小数部分是m, 的小数部分是n,且( 求x的值.
20.(8分)观察以下等式:
第1个等式:1×(2+4)+4×2=2×5+4;
第2个等式:2×(6+4)+4×5=3×8+16;
第3个等式:3×(12+4)+4×10=4×13+36;
第4个等式:4×(20+4)+4×17=5×20+64;
……
按照以上规律,解决下列问题:
(1)写出第5个等式: .
(2)写出你猜想的第n个等式(n为正整数),并证明.
21.(10分)为加快公共领域充电基础设施建设,规范居民安全用电行为,某市计划新建一批智能充电桩.经调研,市场上有A 型、B型两种充电桩,已知A 型充电桩的单价比 B 型充电桩的单价少0.2万元,用12 万元购买A 型充电桩的数量与用16万元购买B型充电桩的数量相等.
(1)求A 型、B型充电桩的单价各是多少.
中小学教育资源及组卷应用平台
(2)该市决定购买A型、B型充电桩共300个,且花费不超过200万元,则至少购买A 型充电桩多少个
22.(10分)有A,B两类正方形,其边长分别为a,b(a>b),现将正方形 B 放在正方形A 的内部得图甲,将正方形A,B并列放置后构造新的正方形得图乙,若图甲和图乙中阴影部分的面积分别为4 和16.
(1)用含a,b的代数式分别表示图甲中阴影部分的面积为 ,图乙中阴影部分的面积为 .
(2)求正方形A,B的面积之和.
(3)三个正方形 A 和两个正方形 B 按图丙的方式摆放,求阴影部分的面积.
23.(12分)
(1)如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC的度数.
(2)如图2,AD∥BC,点 P 在射线 OM 上运动,当点 P 在A、B两点之间运动时,∠ADP=∠α,∠BCP=∠β.求∠CPD、∠α、∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点 P 在A、B两点外侧运动(点P 与A、B、O三点不重合),请你写出∠CPD、∠α、∠β之间的数量关系,并说明理由.
①B 0, 和- 是有理数, 和π是无理数,故无理数共有2个.
故选项A正确; 故选项B错误;a 与a 不是同类项,不能合并,故选项C错误; 故选项D错误.
③A 0.000 002 1=2.1×10 .
④B 当x≠3时,x-3≠0,分式有意义,故选项A不符合题意;当x=3时,分式的分母为0,分式无意义,故选项B符合题意;当x=1时,分式的值为 故选项C不符合题意;若 则x的值不存在,所以分式的值不可能为2,故选项D不符合题意.
⑤D因为a
6D 甲车的速度为 xkm/h,则乙车的速度为1.2x km/h,根据一部分学生乘甲车先出发,5min后其余学生再
乘乙车出发,结果同时到达,可列分式方程为 即
⑦B当输入x的值为16时,取算术平方根是4,4是有理数,再次输入,4的算术平方根是2,2是有理数,再次输入,2的算术平方根是 , 是无理数,所以输出的y的值是
8D 不等式组
解不等式①,得x≥2,解不等式②,得 因为关于x的一元一次不等式组 有解,所以 解得a<4.
9D 因为AB∥CD,所以∠BAC=∠ACD(两直线平行,内错角相等),故选项 A不符合题意;因为∠BAD+∠ADC=180°,所以AB∥CD(同旁内角互补,两直线平行),故选项 B不符合题意;因为AD∥BC,所以∠BCA=∠DAC(两直线平行,内错角相等),故选项C不符合题意;因为∠ABD=∠CDB,所以AB∥CD,无法得出AD∥BC,故选项D符合题意.
10 A 将三个等式左右两边分别相加,得 即 的倒数= 所以
答案 4(x+5)(x-5)
解析 原式
答案 π(答案不唯一)
答案 1:2
解析 因为OD平分∠BOF,所以 因为OE⊥CD,所以∠EOD=90°,所以∠EOB=90°- 因为∠AOF = 180°-∠BOF,所以∠EOB : ∠AOF =
答案 (1)∠2+∠4=∠1+∠3+∠5 (2)40°
解析 (1)如图1,作GM∥AB,FN∥AB,EH∥AB.因为AB∥CD,所以AB∥GM∥FN∥EH∥CD,所以∠1=∠AEH,∠HEG=∠EGM,∠MGF=∠GFN,∠NFC=∠5,所以∠AEG+∠GFC=∠1+∠EGF+∠5,即∠2+∠4=∠1+∠3+∠5.
(2)如图2,作KG∥AB,HQ∥AB,MN与HQ 交于点T.因为 AB∥CD,所以 AB∥KG∥HQ∥CD,所以∠FGK=∠EFA=30°,∠HTN = ∠CNP = 50°.因为∠FGH=90°,所以∠KGH=60°,所以∠GHQ=∠KGH=60°.易知∠HTN=∠QHM+∠M,因为∠M=30°,所以∠QHM=20°,所以∠GHM=∠GHQ-∠QHM=40°.
解析 原式=-9-4+1-2 ………………………… 3分
=-14. 6分
解析 解不等式①,得x>-5,
解不等式②,得x≤4, …………………………… 2分
故原不等式组的解集是-5
解析 原式
……… 4分
因为x-1≠0且2-x≠0,所以x≠1且x≠2,
所以x=0,则原式=1. 6分
解析 (1)如图所示: 4分
(2)7. 8分
详解: 2-3-4=7.
解析 (1)4. 3分
详解:因为16<23<25,所以 所以
因为 且a是整数,所以a=4.
(2)因为4<7<9,所以 所以 所以 …………………… 4 分
因为 的小数部分是m, 的小数部分是n,
所以
6分
因为
所以
所以x-1=1或x-1=-1,
则x=2或x=0. 8分
解析(1)5×(30+4)+4×26=6×29+100. …… 2分
4分
证明:左边
右边
因为左边=右边,
所以等式成立. 8分
解析 (1)设A型充电桩的单价为x万元,则B型充电桩的单价为(x+0.2)万元.
根据题意,得 ………………… 2分解得x=0.6, ……………………………………… 3分
经检验,x=0.6是所列方程的解,且符合题意,所以x+0.2=0.6+0.2=0.8.
答:A型充电桩的单价为0.6万元,B型充电桩的单价为0.8万元. 5分
(2)设购买A 型充电桩m个,则购买B 型充电桩(300-m)个,
根据题意,得0.6m+0.8(300-m)≤200, 8分解得 m≥200,所以m的最小值为200.
答:至少购买A 型充电桩200个. 10分
解析 (1)(a-b) ;2ab. …… 2分
(2)根据题意,得 所以 所以正方形A,B的面积之和为20.……… 6分
(3)由(2)知(
所以ab=8,a-b=2,
所以(
因为a+b>0,所以a+b=6,
所以题图丙中阴影部分的面积为
=a -b +4ab=(a+b)(a-b)+4ab=6×2+4×8=44.…10分
②解析 (1)如图,过点 P作PH∥AB,
则∠BAP+∠APH=180°,所以∠APH=180°-∠BAP=180°-130°=50°. ……
…………………………… … 2分
因为AB∥CD,PH∥AB,所以CD∥PH,所以∠PCD+∠HPC=180°,所以 所以∠APC=∠HPC+∠APH=60°+50°=110°. ……4分
(2)如图,过点P作PF∥AD.
所以∠ADP=∠DPF,即∠α=∠DPF.
因为PF∥AD,AD∥BC,所以PF∥BC,
所以∠FPC=∠PCB,即∠FPC=∠β,
所以∠CPD=∠DPF+∠FPC=∠α+∠β,
即∠CPD=∠α+∠β.……………………………… 8分
(3)当P在A的左侧时,如图:
设PC交AD于点K,因为AD∥BC,
所以∠DKC=∠BCP=∠β.
易知∠DKC=∠CPD+∠ADP,
因为∠ADP=∠α,所以∠β=∠CPD+∠α,
所以∠CPD=∠β-∠α. 10分
当P在B的右侧时,如图:
设PD交BC于点Q,因为AD∥BC,
所以∠ADP=∠DQC=∠α.
易知∠DQC=∠CPD+∠BCP,
所以∠α=∠CPD+∠β,
所以∠CPD=∠α-∠β. 12分
同课章节目录
