10.2 平行线的判定 同步练习(含答案)2024-2025学年沪科版七年级数学下册
文档属性
| 名称 | 10.2 平行线的判定 同步练习(含答案)2024-2025学年沪科版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 257.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:08:48 | ||
图片预览




文档简介
10.2 平行线的判定
第1课时 平行线及同位角、内错角、同旁内角
基础过关全练
知识点1平行线的定义及其基本事实
1.(2024山东淄博沂源期末)在同一平面内,不重合的两条直线的位置关系是 ( )
A.相交 B.平行
C.相交或平行 D.垂直
2.(2023湖北恩施州期中)若直线a,b,c,d有下列关系,则推理正确的是 ( )
A.因为a∥b,b∥c,所以c∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
3.分类讨论思想已知∠AOB,P是平面内任一点,过点 P 画一条直线与 OA 平行,则这样的直线 ( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
4.如图,已知OM∥a,ON∥a,则O、M、N三点共线,理由是 .
如图,AB∥CD,过点E作EF∥AB,则EF与CD的位置关系是 ,理由是
知识点 2 同位角、内错角、同旁内角
6.(2024安徽淮南月考)如图,直线AB,CD 被直线EF所截,则∠1与∠2是 ( )
A.同位角 B.内错角 C.同旁内角D.对顶角
7.(2024广西玉林玉州期中)如图所示,直线a,b被直线c所截,则∠1的同位角是 ( )
A.∠2 B.∠3 C.∠4 D.无
8.(2024安徽宿州埔桥月考)如图,下列说法错误的是 ( )
A.∠2与∠4是同位角
B.∠2与∠3 是同旁内角
C.∠1与∠2是内错角
D.∠1与∠A是内错角
9.如图,当直线AC、DG被直线 CD 所截时,∠2 的内错角是 .∠AEF 的同位角是 .∠1的同旁内角是 .
10.如图,直线AB,CD,EF两两相交,回答下列问题:
(1)如果直线 AB,EF 被直线 CD 所截,那么∠1与∠2,∠3 与∠4,∠2 与∠4 是什么位置关系的角
(2)如果直线CD,EF被直线AB 所截,那么∠1与∠5,∠4与∠5是什么位置关系的角
(3)如果∠2与∠5是同位角,那么它们是哪两条直线被哪一条直线所截形成的
能力提升全练
11.数学课上老师用双手形象表示了“三线八角”图形,如图所示(两大拇指代表被截直线,两食指代表截线).从左至右依次表示 ( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
12.2024年五一假期,香洲区举办了第六届风筝会.如图所示的风筝骨架中,与∠3构成同旁内角的是 ( )
A.∠1 B.∠2 C.∠4 D.∠5
13.如图,下列说法错误的是 ( )
A.∠1与∠2 是对顶角
B.∠2与∠5是内错角
C.∠2与∠4是同旁内角
D.∠3与∠4是同位角
14.如图,把一根筷子的一端放在水里,一端露出水面,筷子变弯了 其实没有,这是光的折射现象,光从空气射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角.
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上弯折了多少度 请说明理由.
15.如图1,两条直线l ,l 被第三条直线l 所截,若同旁内角∠α,∠β满足∠β=∠α+30°,则称∠β是∠α的关联角.
(1)已知∠β是∠α的关联角,当∠α=50°时,∠β= .
(2)如图2,已知∠AGH 是∠CHG 的关联角,那么∠DHG 是∠BGH 的关联角吗 为什么
第2课时平行线的判定
基础过关全练
知识点 3 平行线的判定
1.如图,当∠A=∠CBE 时,下列结论正确的是 ( )
A. AD∥BC B. BC∥DC
C. AD∥AE D. AB∥DC
2.(2024安徽合肥蜀山期末)下列图形中,由∠1=∠2 能得到AB∥CD 的是 ( )
3.如图,小明在地图上量得 ∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
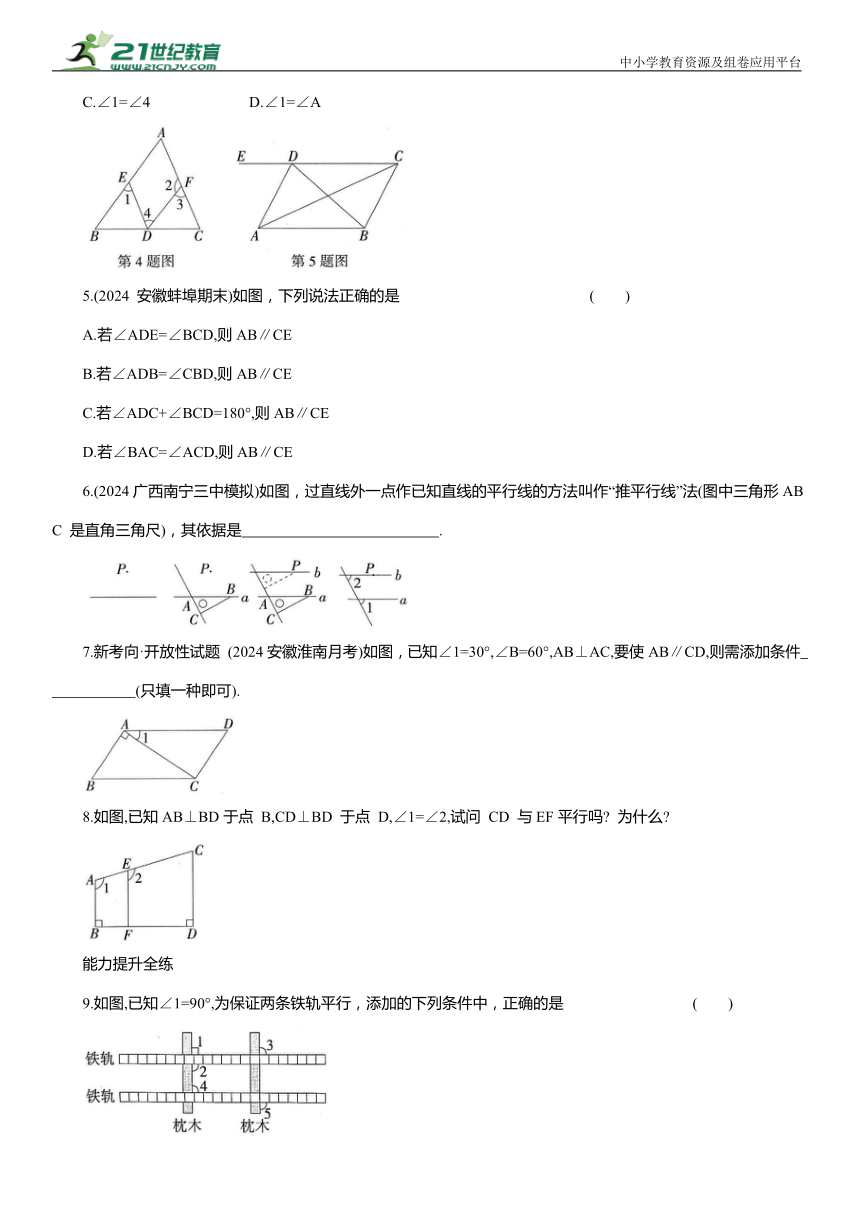
4.(2024安徽阜阳期末)如图,在下列给出的条件中,不能判定AB∥DF的是 ( )
A.∠A=∠3 B.∠A+∠2=180°
C.∠1=∠4 D.∠1=∠A
5.(2024 安徽蚌埠期末)如图,下列说法正确的是 ( )
A.若∠ADE=∠BCD,则AB∥CE
B.若∠ADB=∠CBD,则AB∥CE
C.若∠ADC+∠BCD=180°,则AB∥CE
D.若∠BAC=∠ACD,则AB∥CE
6.(2024广西南宁三中模拟)如图,过直线外一点作已知直线的平行线的方法叫作“推平行线”法(图中三角形ABC 是直角三角尺),其依据是 .
7.新考向·开放性试题 (2024安徽淮南月考)如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加条件 (只填一种即可).
8.如图,已知AB⊥BD于点 B,CD⊥BD 于点 D,∠1=∠2,试问 CD 与EF平行吗 为什么
能力提升全练
9.如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是 ( )
A.∠2=90° B.∠3=90°
C.∠4=90° D.∠5=90°
10.将一副直角三角尺按如图所示的方式放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则下列结论:
①∠1=∠3;②∠CAD+∠2=180°;③若∠2=30°,则有AC∥DE;④若∠2=30°,则BC∥AD.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
11.(2024安徽合肥庐江期末,19, )如图,已知E,F分别在 AB 和 CD 上,∠1=∠D,∠2 与∠C互余,AF⊥CE 于 G.求证:AB∥CD.
12.如图,台球运动中母球P击中桌边的点 A,经桌边反弹后击中相邻桌边的点B,再次反弹击中球C.(提示:∠1=∠2,∠3=∠4)
(1)若∠1=32°,求∠PAB 的度数.
(2)已知∠2+∠3=90°,母球P 经过的路线 BC与PA一定平行吗 请说明理由.
素养探究全练
13.推理能力 如图,直线AB 和 CD被直线EF所截.
(1)如图1,EG平分∠BEF,FH 平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足 时,AB∥CD.
(2)如图2,EG 平分∠MEB,FH 平分∠DFE(平分的是一对同位角),则∠1与∠2 满足 时,AB∥CD.
(3)如图 3,EG 平分∠AEF,FH 平分∠DFE(平分的是一对内错角),则∠1 与∠2 满足什么条件时,AB∥CD 为什么
中小学教育资源及组卷应用平台
10.2 平行线的判定
第1 课时 平行线及同位角、内错角、同旁内角
基础过关全练
①C在同一平面内,不重合的两条直线只有两种位置关系,即相交和平行,故选C.
②C如果两条直线和第三条直线平行,那么这两条直线平行,由此判断选项 C正确.
③D ①若点 P 在直线OA 上,则不能画出与OA 平行的直线;②若点 P 不在直线OA上,则过点 P 有且只有一条直线与OA平行,所以这样的直线有一条或不存在.
④ 答案 过直线外一点有且只有一条直线与这条直线平行
⑤答案 EF∥CD;如果两条直线和第三条直线平行,那么这两条直线平行
解析 由题图和已知条件可知,AB∥CD,EF∥AB,则EF∥CD,符合平行线基本事实的推论.
6C ∠1和∠2位于EF同一侧且位于AB,CD之间,故它们是同旁内角.
⑦A两条直线a,b被第三条直线c所截,在截线c的同旁,且在被截直线a,b的同一侧的角,我们把这样的两个角叫作同位角,故∠1的同位角是∠2.
8C∠1 和∠2之间没有位置角关系.
⑨答案 ∠ACD;∠ACD、∠ACB;∠ACD、∠ACB、∠EFD
⑩解析 (1)∠1与∠2是同位角,∠3与∠4是内错角,∠2与∠4是同旁内角.
(2)∠1与∠5是同旁内角,∠4与∠5是内错角.
(3)是直线AB,CD被直线EF 所截形成的.
能力提升全练
11 D 本题用手将“三线八角”表示出来,将所学的知识融入生活,构思巧妙.根据同位角、内错角、同旁内角的概念,可知从左至右依次表示同位角、内错角、同旁内角.
12 A 由题图得∠1 与∠3构成同旁内角.
①D∠1与∠2是对顶角,故选项 A说法正确;∠2与∠5是内错角,故选项 B说法正确;∠2与∠4是同旁内角,故选项C说法正确;∠3与∠4是同旁内角,
故选项D说法错误.故选 D.
解析 (1)∠1 的同旁内角有∠MOE,∠AOE,∠ADE,∠2的内错角有∠MOE,∠AOE.
(2)水下部分向上弯折了30度.理由如下:
因为∠BOM=145°,
所以∠AOM=180°-∠BOM=35°,
所以
所以水下部分向上弯折了30度.
解析 (1)因为∠β是∠α的关联角,∠α=50°,所以.
故答案为80°.
(2)∠DHG是∠BGH的关联角.理由如下:
因为∠AGH是∠CHG的关联角,
所以∠AGH=∠CHG+30°,所以∠AGH-∠CHG=30°.
因为∠DHG=180°-∠CHG,∠BGH=180°-∠AGH,
所以∠DHG-∠BGH=180°-∠CHG-(180°-∠AGH)
=∠AGH-∠CHG=30°,
所以∠DHG=∠BGH+30°,
又因为∠DHG和∠BGH 是同旁内角,
所以∠DHG是∠BGH的关联角.
第2 课时 平行线的判定
基础过关全练
①A 根据“同位角相等,两直线平行”可知,当∠A=∠CBE时,AD∥BC.
②C选项A中,由∠1=∠2不能得到AB∥CD;选项B中,由∠1=∠2得到AD∥BC,不能得到AB∥CD;选项C中,如图,因为∠1=∠2,∠2=∠DME,所以∠1=∠DME,所以AB∥CD;选项D中,由∠1=∠2不能得到AB∥CD.故选 C.
③B因为∠1和∠2是内错角,∠1=∠2,所以幸福大街与平安大街互相平行(内错角相等,两直线平行).故选 B.
④D因为∠A=∠3,所以AB∥DF(同位角相等,两直线平行),故选项A不符合题意;因为∠A+∠2=180°,所以AB∥DF(同旁内角互补,两直线平行),故选项B不符合题意;因为∠1=∠4,所以AB∥DF(内错角相等,两直线平行),故选项C不符合题意;因为∠1=∠A,所以AC∥DE(同位角相等,两直线平行),不能判定AB∥DF,故选项 D符合题意.故选D.
5D 若∠ADE=∠BCD,则AD∥BC,故选项 A说法错误,不符合题意;
若∠ADB=∠CBD,则AD∥BC,故选项B说法错误,不符合题意;
若∠ADC+∠BCD=180°,则AD∥BC,故选项C说法错误,不符合题意;
若∠BAC=∠ACD,则AB∥CE,故选项D说法正确,符合题意.故选 D.
⑥答案 同位角相等,两直线平行
解析 由题意可知∠1=∠2,由“同位角相等,两直线平行”可知a∥b.
⑦答案 ∠ACD=90°(答案不唯一)
解析 因为AB⊥AC,所以∠BAC=90°.若∠ACD=90°,则∠BAC=∠ACD,所以AB∥CD,所以要使AB∥CD,可添加条件∠ACD=90°(答案不唯一).
⑧解析 CD与EF平行.理由如下:
因为∠1=∠2,所以AB∥EF.
因为AB⊥BD,CD⊥BD,
所以AB∥CD,
所以CD∥EF.
能力提升全练
9C根据同位角相等,两直线平行,可添加条件∠4=∠1=90°.故选 C.
10B 因为∠1+∠2=90°,∠3+∠2=90°,所以∠1=∠3,故结论①正确;∠CAD+∠2=∠1+∠2+∠3+∠2 ,故结论②正确;因为∠2=30°,所以∠1=60°=∠E,所以AC∥DE,故结论③正确;因为∠2=30°,∠B=45°,所以∠3=60°≠∠B,所以BC与AD 不平行,故结论④不正确.故选 B.
证明 因为AF⊥CE,所以∠CGF=90°.
所以∠1+∠C=90°.
又因为∠2+∠C=90°,所以∠1=∠2.
因为∠1=∠D,
所以∠2=∠D,
所以AB∥CD.
解析 (1)因为∠1=32°,∠1=∠2,∠1+∠PAB+∠2=180°,
所以
(2)BC∥PA.理由如下:
因为∠1=∠2,∠PAB=180°-∠1-∠2,
所以∠PAB=180°-2∠2.
同理,∠ABC=180°-2∠3.
因为∠2+∠3=90°,
所以∠PAB+∠ABC=360°-2(∠2+∠3)=180°,所以BC∥PA.
素养探究全练
解析 (1)∠1+∠2=90°.
详解:因为EG平分∠BEF,FH平分∠DFE,
所以∠BEF=2∠1,∠DFE=2∠2.
因为∠1+∠2=90°,
所以∠BEF+∠DFE=180°,所以AB∥CD.
故∠1+∠2=90°时,AB∥CD.
(2)∠1=∠2.
详解:因为EG平分∠MEB,FH平分∠DFE,所以∠MEB=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠MEB=∠DFE,所以AB∥CD.
故∠1=∠2时,AB∥CD.
(3)∠1=∠2时,AB∥CD.
理由:因为EG平分∠AEF,FH平分∠DFE,
所以∠AEF=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠AEF=∠DFE,所以AB∥CD.
第1课时 平行线及同位角、内错角、同旁内角
基础过关全练
知识点1平行线的定义及其基本事实
1.(2024山东淄博沂源期末)在同一平面内,不重合的两条直线的位置关系是 ( )
A.相交 B.平行
C.相交或平行 D.垂直
2.(2023湖北恩施州期中)若直线a,b,c,d有下列关系,则推理正确的是 ( )
A.因为a∥b,b∥c,所以c∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
3.分类讨论思想已知∠AOB,P是平面内任一点,过点 P 画一条直线与 OA 平行,则这样的直线 ( )
A.有且仅有一条 B.有两条
C.不存在 D.有一条或不存在
4.如图,已知OM∥a,ON∥a,则O、M、N三点共线,理由是 .
如图,AB∥CD,过点E作EF∥AB,则EF与CD的位置关系是 ,理由是
知识点 2 同位角、内错角、同旁内角
6.(2024安徽淮南月考)如图,直线AB,CD 被直线EF所截,则∠1与∠2是 ( )
A.同位角 B.内错角 C.同旁内角D.对顶角
7.(2024广西玉林玉州期中)如图所示,直线a,b被直线c所截,则∠1的同位角是 ( )
A.∠2 B.∠3 C.∠4 D.无
8.(2024安徽宿州埔桥月考)如图,下列说法错误的是 ( )
A.∠2与∠4是同位角
B.∠2与∠3 是同旁内角
C.∠1与∠2是内错角
D.∠1与∠A是内错角
9.如图,当直线AC、DG被直线 CD 所截时,∠2 的内错角是 .∠AEF 的同位角是 .∠1的同旁内角是 .
10.如图,直线AB,CD,EF两两相交,回答下列问题:
(1)如果直线 AB,EF 被直线 CD 所截,那么∠1与∠2,∠3 与∠4,∠2 与∠4 是什么位置关系的角
(2)如果直线CD,EF被直线AB 所截,那么∠1与∠5,∠4与∠5是什么位置关系的角
(3)如果∠2与∠5是同位角,那么它们是哪两条直线被哪一条直线所截形成的
能力提升全练
11.数学课上老师用双手形象表示了“三线八角”图形,如图所示(两大拇指代表被截直线,两食指代表截线).从左至右依次表示 ( )
A.同旁内角、同位角、内错角
B.同位角、内错角、对顶角
C.对顶角、同位角、同旁内角
D.同位角、内错角、同旁内角
12.2024年五一假期,香洲区举办了第六届风筝会.如图所示的风筝骨架中,与∠3构成同旁内角的是 ( )
A.∠1 B.∠2 C.∠4 D.∠5
13.如图,下列说法错误的是 ( )
A.∠1与∠2 是对顶角
B.∠2与∠5是内错角
C.∠2与∠4是同旁内角
D.∠3与∠4是同位角
14.如图,把一根筷子的一端放在水里,一端露出水面,筷子变弯了 其实没有,这是光的折射现象,光从空气射入水中,光的传播方向发生了改变.
(1)请指出∠1的同旁内角与∠2的内错角.
(2)若测得∠AOE=65°,∠BOM=145°,从水面上看斜插入水中的筷子,水下部分向上弯折了多少度 请说明理由.
15.如图1,两条直线l ,l 被第三条直线l 所截,若同旁内角∠α,∠β满足∠β=∠α+30°,则称∠β是∠α的关联角.
(1)已知∠β是∠α的关联角,当∠α=50°时,∠β= .
(2)如图2,已知∠AGH 是∠CHG 的关联角,那么∠DHG 是∠BGH 的关联角吗 为什么
第2课时平行线的判定
基础过关全练
知识点 3 平行线的判定
1.如图,当∠A=∠CBE 时,下列结论正确的是 ( )
A. AD∥BC B. BC∥DC
C. AD∥AE D. AB∥DC
2.(2024安徽合肥蜀山期末)下列图形中,由∠1=∠2 能得到AB∥CD 的是 ( )
3.如图,小明在地图上量得 ∠1=∠2,由此判断幸福大街与平安大街互相平行,他判断的依据是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
4.(2024安徽阜阳期末)如图,在下列给出的条件中,不能判定AB∥DF的是 ( )
A.∠A=∠3 B.∠A+∠2=180°
C.∠1=∠4 D.∠1=∠A
5.(2024 安徽蚌埠期末)如图,下列说法正确的是 ( )
A.若∠ADE=∠BCD,则AB∥CE
B.若∠ADB=∠CBD,则AB∥CE
C.若∠ADC+∠BCD=180°,则AB∥CE
D.若∠BAC=∠ACD,则AB∥CE
6.(2024广西南宁三中模拟)如图,过直线外一点作已知直线的平行线的方法叫作“推平行线”法(图中三角形ABC 是直角三角尺),其依据是 .
7.新考向·开放性试题 (2024安徽淮南月考)如图,已知∠1=30°,∠B=60°,AB⊥AC,要使AB∥CD,则需添加条件 (只填一种即可).
8.如图,已知AB⊥BD于点 B,CD⊥BD 于点 D,∠1=∠2,试问 CD 与EF平行吗 为什么
能力提升全练
9.如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是 ( )
A.∠2=90° B.∠3=90°
C.∠4=90° D.∠5=90°
10.将一副直角三角尺按如图所示的方式放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则下列结论:
①∠1=∠3;②∠CAD+∠2=180°;③若∠2=30°,则有AC∥DE;④若∠2=30°,则BC∥AD.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
11.(2024安徽合肥庐江期末,19, )如图,已知E,F分别在 AB 和 CD 上,∠1=∠D,∠2 与∠C互余,AF⊥CE 于 G.求证:AB∥CD.
12.如图,台球运动中母球P击中桌边的点 A,经桌边反弹后击中相邻桌边的点B,再次反弹击中球C.(提示:∠1=∠2,∠3=∠4)
(1)若∠1=32°,求∠PAB 的度数.
(2)已知∠2+∠3=90°,母球P 经过的路线 BC与PA一定平行吗 请说明理由.
素养探究全练
13.推理能力 如图,直线AB 和 CD被直线EF所截.
(1)如图1,EG平分∠BEF,FH 平分∠DFE(平分的是一对同旁内角),则∠1与∠2满足 时,AB∥CD.
(2)如图2,EG 平分∠MEB,FH 平分∠DFE(平分的是一对同位角),则∠1与∠2 满足 时,AB∥CD.
(3)如图 3,EG 平分∠AEF,FH 平分∠DFE(平分的是一对内错角),则∠1 与∠2 满足什么条件时,AB∥CD 为什么
中小学教育资源及组卷应用平台
10.2 平行线的判定
第1 课时 平行线及同位角、内错角、同旁内角
基础过关全练
①C在同一平面内,不重合的两条直线只有两种位置关系,即相交和平行,故选C.
②C如果两条直线和第三条直线平行,那么这两条直线平行,由此判断选项 C正确.
③D ①若点 P 在直线OA 上,则不能画出与OA 平行的直线;②若点 P 不在直线OA上,则过点 P 有且只有一条直线与OA平行,所以这样的直线有一条或不存在.
④ 答案 过直线外一点有且只有一条直线与这条直线平行
⑤答案 EF∥CD;如果两条直线和第三条直线平行,那么这两条直线平行
解析 由题图和已知条件可知,AB∥CD,EF∥AB,则EF∥CD,符合平行线基本事实的推论.
6C ∠1和∠2位于EF同一侧且位于AB,CD之间,故它们是同旁内角.
⑦A两条直线a,b被第三条直线c所截,在截线c的同旁,且在被截直线a,b的同一侧的角,我们把这样的两个角叫作同位角,故∠1的同位角是∠2.
8C∠1 和∠2之间没有位置角关系.
⑨答案 ∠ACD;∠ACD、∠ACB;∠ACD、∠ACB、∠EFD
⑩解析 (1)∠1与∠2是同位角,∠3与∠4是内错角,∠2与∠4是同旁内角.
(2)∠1与∠5是同旁内角,∠4与∠5是内错角.
(3)是直线AB,CD被直线EF 所截形成的.
能力提升全练
11 D 本题用手将“三线八角”表示出来,将所学的知识融入生活,构思巧妙.根据同位角、内错角、同旁内角的概念,可知从左至右依次表示同位角、内错角、同旁内角.
12 A 由题图得∠1 与∠3构成同旁内角.
①D∠1与∠2是对顶角,故选项 A说法正确;∠2与∠5是内错角,故选项 B说法正确;∠2与∠4是同旁内角,故选项C说法正确;∠3与∠4是同旁内角,
故选项D说法错误.故选 D.
解析 (1)∠1 的同旁内角有∠MOE,∠AOE,∠ADE,∠2的内错角有∠MOE,∠AOE.
(2)水下部分向上弯折了30度.理由如下:
因为∠BOM=145°,
所以∠AOM=180°-∠BOM=35°,
所以
所以水下部分向上弯折了30度.
解析 (1)因为∠β是∠α的关联角,∠α=50°,所以.
故答案为80°.
(2)∠DHG是∠BGH的关联角.理由如下:
因为∠AGH是∠CHG的关联角,
所以∠AGH=∠CHG+30°,所以∠AGH-∠CHG=30°.
因为∠DHG=180°-∠CHG,∠BGH=180°-∠AGH,
所以∠DHG-∠BGH=180°-∠CHG-(180°-∠AGH)
=∠AGH-∠CHG=30°,
所以∠DHG=∠BGH+30°,
又因为∠DHG和∠BGH 是同旁内角,
所以∠DHG是∠BGH的关联角.
第2 课时 平行线的判定
基础过关全练
①A 根据“同位角相等,两直线平行”可知,当∠A=∠CBE时,AD∥BC.
②C选项A中,由∠1=∠2不能得到AB∥CD;选项B中,由∠1=∠2得到AD∥BC,不能得到AB∥CD;选项C中,如图,因为∠1=∠2,∠2=∠DME,所以∠1=∠DME,所以AB∥CD;选项D中,由∠1=∠2不能得到AB∥CD.故选 C.
③B因为∠1和∠2是内错角,∠1=∠2,所以幸福大街与平安大街互相平行(内错角相等,两直线平行).故选 B.
④D因为∠A=∠3,所以AB∥DF(同位角相等,两直线平行),故选项A不符合题意;因为∠A+∠2=180°,所以AB∥DF(同旁内角互补,两直线平行),故选项B不符合题意;因为∠1=∠4,所以AB∥DF(内错角相等,两直线平行),故选项C不符合题意;因为∠1=∠A,所以AC∥DE(同位角相等,两直线平行),不能判定AB∥DF,故选项 D符合题意.故选D.
5D 若∠ADE=∠BCD,则AD∥BC,故选项 A说法错误,不符合题意;
若∠ADB=∠CBD,则AD∥BC,故选项B说法错误,不符合题意;
若∠ADC+∠BCD=180°,则AD∥BC,故选项C说法错误,不符合题意;
若∠BAC=∠ACD,则AB∥CE,故选项D说法正确,符合题意.故选 D.
⑥答案 同位角相等,两直线平行
解析 由题意可知∠1=∠2,由“同位角相等,两直线平行”可知a∥b.
⑦答案 ∠ACD=90°(答案不唯一)
解析 因为AB⊥AC,所以∠BAC=90°.若∠ACD=90°,则∠BAC=∠ACD,所以AB∥CD,所以要使AB∥CD,可添加条件∠ACD=90°(答案不唯一).
⑧解析 CD与EF平行.理由如下:
因为∠1=∠2,所以AB∥EF.
因为AB⊥BD,CD⊥BD,
所以AB∥CD,
所以CD∥EF.
能力提升全练
9C根据同位角相等,两直线平行,可添加条件∠4=∠1=90°.故选 C.
10B 因为∠1+∠2=90°,∠3+∠2=90°,所以∠1=∠3,故结论①正确;∠CAD+∠2=∠1+∠2+∠3+∠2 ,故结论②正确;因为∠2=30°,所以∠1=60°=∠E,所以AC∥DE,故结论③正确;因为∠2=30°,∠B=45°,所以∠3=60°≠∠B,所以BC与AD 不平行,故结论④不正确.故选 B.
证明 因为AF⊥CE,所以∠CGF=90°.
所以∠1+∠C=90°.
又因为∠2+∠C=90°,所以∠1=∠2.
因为∠1=∠D,
所以∠2=∠D,
所以AB∥CD.
解析 (1)因为∠1=32°,∠1=∠2,∠1+∠PAB+∠2=180°,
所以
(2)BC∥PA.理由如下:
因为∠1=∠2,∠PAB=180°-∠1-∠2,
所以∠PAB=180°-2∠2.
同理,∠ABC=180°-2∠3.
因为∠2+∠3=90°,
所以∠PAB+∠ABC=360°-2(∠2+∠3)=180°,所以BC∥PA.
素养探究全练
解析 (1)∠1+∠2=90°.
详解:因为EG平分∠BEF,FH平分∠DFE,
所以∠BEF=2∠1,∠DFE=2∠2.
因为∠1+∠2=90°,
所以∠BEF+∠DFE=180°,所以AB∥CD.
故∠1+∠2=90°时,AB∥CD.
(2)∠1=∠2.
详解:因为EG平分∠MEB,FH平分∠DFE,所以∠MEB=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠MEB=∠DFE,所以AB∥CD.
故∠1=∠2时,AB∥CD.
(3)∠1=∠2时,AB∥CD.
理由:因为EG平分∠AEF,FH平分∠DFE,
所以∠AEF=2∠1,∠DFE=2∠2.
因为∠1=∠2,
所以∠AEF=∠DFE,所以AB∥CD.
