第五章 5.3诱导公式--人教A版高中数学必修第一册教学课件(共34张PPT)
文档属性
| 名称 | 第五章 5.3诱导公式--人教A版高中数学必修第一册教学课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:21:09 | ||
图片预览







文档简介
(共34张PPT)
5.3 诱导公式
第五章 三角函数
数学
学习目标
①借助单位圆,推导出正弦、余弦和正切的诱导公式.
②能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题.
③了解未知到已知、复杂到简单的转化过程,培养化归思想.
学习重难点
重点:
诱导公式的记忆、理解、运用.
难点:
诱导公式的推导、记忆及符号的判断.
课堂导入
复习情境
1.任意角的三角函数的定义
设角α是一个任意角,α∈R,它的终边与单位圆交于点P(x,y).
(1)y叫做α的正弦函数,记作sin α,即y=sin α;
(2)x叫做α的余弦函数,记作cos α,即x=cos α;
(3)叫做α的正切,记作tan α,即=tan α(x≠0).
课堂导入
复习情境
2.诱导公式一
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α,
其中,k∈Z.
终边相同的角的同一三角函数的值相等.
课堂探究
思考1
(1)终边相同的角的同一三角函数值有什么关系
相等.
(2)角 α与α的终边有何位置关系
终边关于x轴对称.
(3)角π α与α的终边有何位置关系
终边关于y轴对称.
(4)角π+α与α的终边有何位置关系
终边关于原点对称.
问题引入
课堂探究
思考2 已知任意角α的终边与单位圆相交于点P(x,y),请同学们思考回答点P关于原点、x轴、y轴对称的三个点的坐标分别是什么
点P(x,y)关于原点的对称点P1的坐标是( x, y),
点P(x,y)关于x轴的对称点P2的坐标是(x, y),
点P(x,y)关于y轴的对称点P3的坐标是( x,y).
问题引入
课堂探究
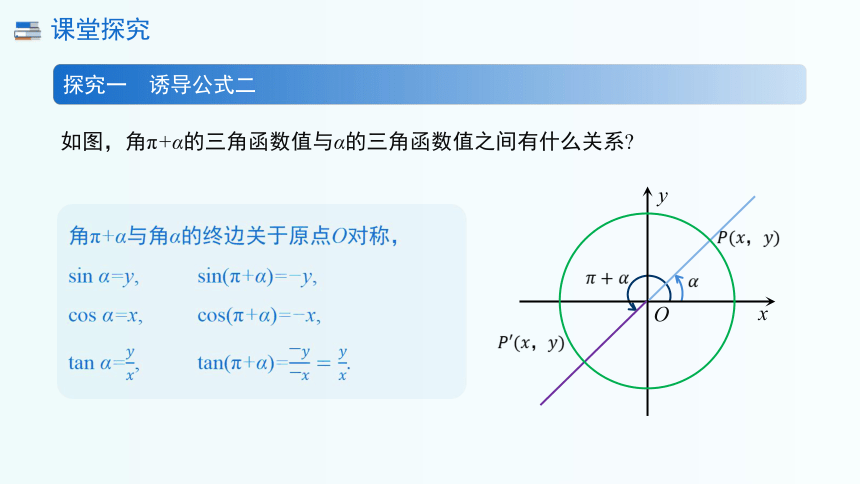
探究一 诱导公式二
如图,角π+α的三角函数值与α的三角函数值之间有什么关系
角π+α与角α的终边关于原点O对称,
sin α=y, sin(π+α)= y,
cos α=x, cos(π+α)= x,
tan α=, tan(π+α)=.
x
y
O
课堂探究
x
y
O
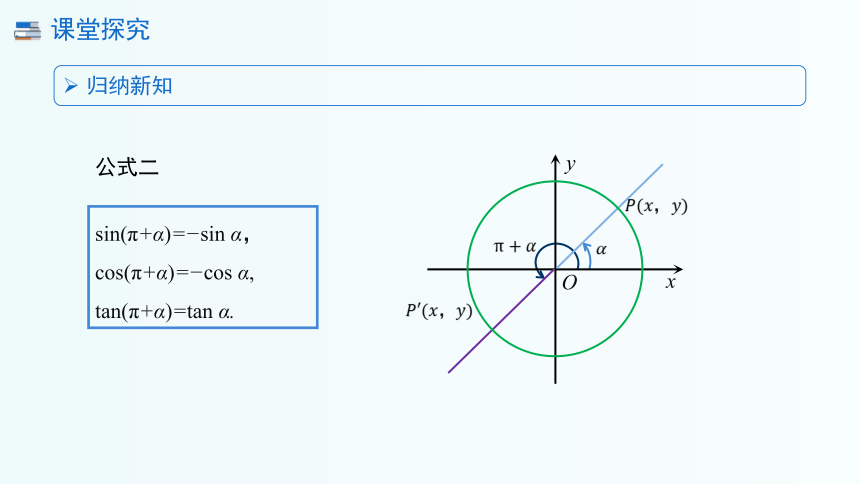
公式二
归纳新知
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
课堂探究
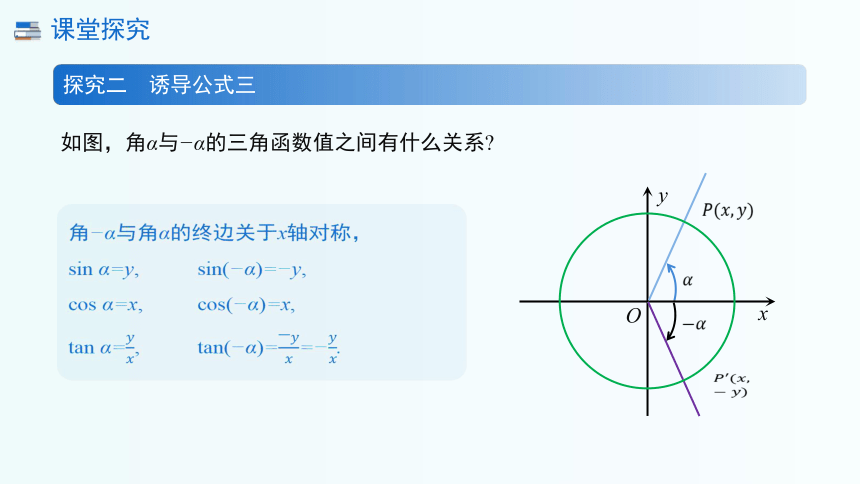
探究二 诱导公式三
如图,角α与 α的三角函数值之间有什么关系
角 α与角α的终边关于x轴对称,
sin α=y, sin( α)= y,
cos α=x, cos( α)=x,
tan α=, tan( α)== .
x
y
O
课堂探究
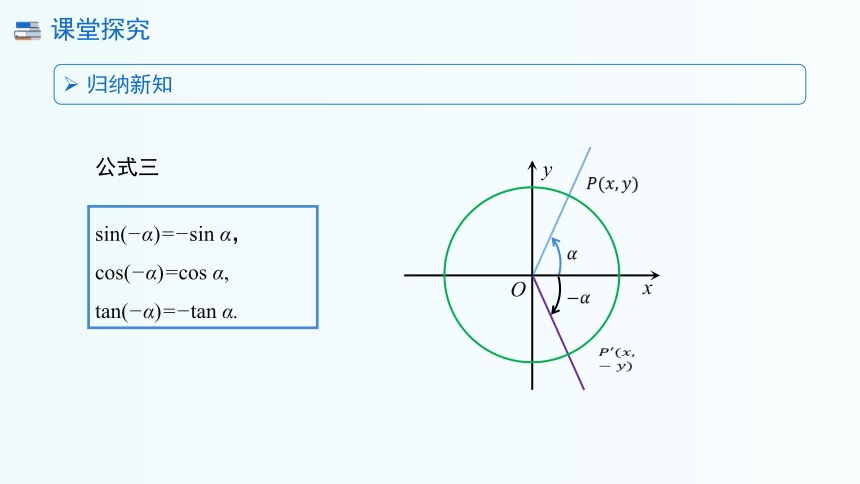
归纳新知
公式三
x
y
O
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
课堂探究
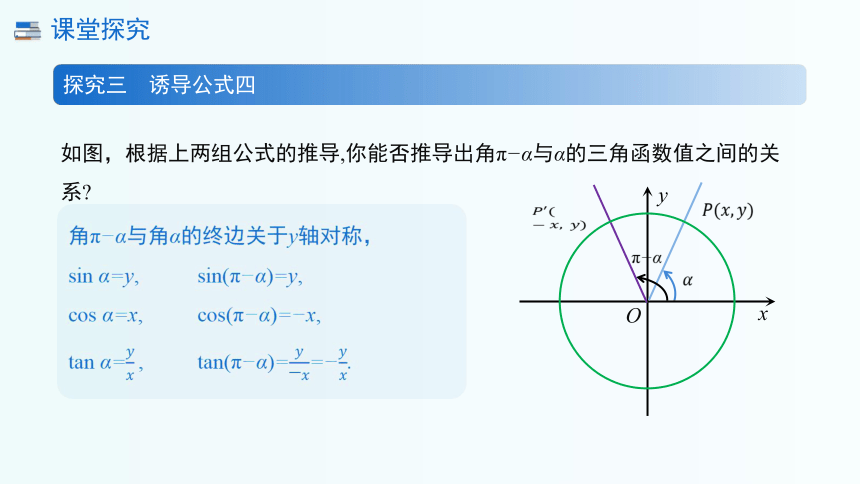
探究三 诱导公式四
如图,根据上两组公式的推导,你能否推导出角π α与α的三角函数值之间的关系
角π α与角α的终边关于y轴对称,
sin α=y, sin(π α)=y,
cos α=x, cos(π α)= x,
tan α= tan(π α)== .
x
y
O
课堂探究
归纳新知
公式四
x
y
O
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
课堂探究
思考3 诱导公式一、二、三、四有什么规律
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α,
其中,k∈Z.
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
公式一
公式二
公式四
公式三
α+k·2π(k∈Z), α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
函数名不变,符号看象限
课堂探究
例1 求下列三角函数值:
(1)cos 225°; (2)sin;
(3)sin( ); (4)tan( 2 040°).
解 (1)cos 225°=cos(180°+45°)= cos 45°= .
(2)sin=sin(2π+)=sin=sin(π )=sin.
(3)sin( )= sin= sin(5π+)= ( sin)=.
(4)tan( 2 040°)= tan 2 040°= tan(6×360° 120°)=tan 120°=tan(180° 60°)= tan 60°= .
课堂探究
思考4 通过例题,你对诱导公式一、二、三、四有什么进一步的认识 你能归纳把任意角的三角函数化为锐角三角函数的步骤吗
利用公式一~公式四把任意角的三角函数转化为锐角三角函数,一般可按下列步骤进行:
上述步骤体现了由未知转化为已知的转化与化归思想方法.
任意负角的
三角函数
任意正角的
三角函数
的角的三角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
课堂探究
例2 化简:.
解 原式== cos α.
课堂探究
探究四 诱导公式五
如图,作点P(x,y)关于直线y=x的对称点P1(y,x),以OP1为终边的角γ与角α有什么关系 角γ与角α的三角函数值之间有什么关系
γ=2kπ+( α) (k∈Z).
公式五
sin( α)=cos α,
cos( α)=sin α.
课堂探究
探究五 诱导公式六
如图,作点P1(y,x)关于y轴的对称点P2,又能得到什么结论
公式六
sin(+α)=cos α,
cos(+α)= sin α.
课堂探究
思考5 你能概括一下公式五、六的共同特点和规律吗
±α的正弦(余弦)函数值,等于α的余弦(正弦)函数值,
前面加上一个把α看成锐角时原函数值的符号.
课堂探究
思考6 诱导公式可统一为±α(k∈Z)的三角函数与α的三角函数之间的关系,你有什么办法记住这些公式
sin( α)=cos α,
cos( α)=sin α.
sin(+α)=cos α,
cos(+α)= sin α.
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
口诀:奇变偶不变,符号看象限.
课堂探究
口诀的意义:
k·±α(k∈Z)的三角函数值,
(1)当k为偶数时,
等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;
(2)当k为奇数时,
等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号.
课堂探究
例3 证明:
(1)sin( α)= cos α;
(2)cos( α)= sin α.
证明 (1)sin( α)=sin= sin( α)= cos α.
(2)cos( α)=cos= cos( α)= sin α.
课堂探究
例4 化简:
.
解 原式=
==
= tan α.
课堂探究
例5 已知sin(53 α)=,且 270<α< 90,求sin(37+α)的值.
解 因为 270<α< 90,所以143<53 α<323.
又因为sin(53 α)>0,
所以143<53 α<180 ,
所以cos(53 α)= ,
所以sin(37+α)=sin[90 (53 α)]=cos(53 α)= .
评价反馈
1. 下列各式不正确的是( )
A.sin(α+180°)= sin α
B.cos( α+β)= cos(α β)
C.sin( α 360°)= sin α
D.cos( α β)=cos(α+β)
B
解析 cos( α+β)=cos [ (α β)]=cos(α β),故B项错误.
评价反馈
2. sin 600°的值为( )
A. B.
C. D.
D
解析 sin 600°=sin(720° 120°)
= sin 120°= sin(180° 60°)
= sin 60°= .
故选D.
评价反馈
3. cos 1 030°= ( )
A.cos 50° B. cos 50°
C.sin 50° D. sin 50°
A
解析 cos 1 030°=cos(3×360° 50°)
=cos( 50°)
=cos 50°.
评价反馈
4. 若sin<0,且cos>0,则θ是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
B
解析 因为sin=cos θ<0,
cos=sin θ>0,
所以θ是第二象限角,
故选B.
评价反馈
5. 已知sin φ=,求cos+sin(3π φ)的值.
解 ∵sin φ=,
∴cos=cos(6π +φ)=cos( +φ)=cos( φ)=sin φ=,
∴cos+sin(3π φ)=+sin(π φ)=+sin φ=.
课堂小结
1.诱导公式.
2.诱导公式的记忆.
3.利用诱导公式求任意角的三角函数值的步骤.
我们今天都学习了哪些知识
思考问题
课堂小结
三角函数的简化过程图:
归纳总结
任意负角的
三角函数
任意正角的
三角函数
的角的三角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
三角函数的简化过程口诀:负化正,正化小,化到锐角为终了.
诱导公式记忆口诀:奇变偶不变,符号看象限.
布置作业
完成教材第194195页习题5.3第4,6题.
谢谢大家
5.3 诱导公式
第五章 三角函数
数学
学习目标
①借助单位圆,推导出正弦、余弦和正切的诱导公式.
②能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,并解决有关三角函数求值、化简和恒等式证明问题.
③了解未知到已知、复杂到简单的转化过程,培养化归思想.
学习重难点
重点:
诱导公式的记忆、理解、运用.
难点:
诱导公式的推导、记忆及符号的判断.
课堂导入
复习情境
1.任意角的三角函数的定义
设角α是一个任意角,α∈R,它的终边与单位圆交于点P(x,y).
(1)y叫做α的正弦函数,记作sin α,即y=sin α;
(2)x叫做α的余弦函数,记作cos α,即x=cos α;
(3)叫做α的正切,记作tan α,即=tan α(x≠0).
课堂导入
复习情境
2.诱导公式一
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α,
其中,k∈Z.
终边相同的角的同一三角函数的值相等.
课堂探究
思考1
(1)终边相同的角的同一三角函数值有什么关系
相等.
(2)角 α与α的终边有何位置关系
终边关于x轴对称.
(3)角π α与α的终边有何位置关系
终边关于y轴对称.
(4)角π+α与α的终边有何位置关系
终边关于原点对称.
问题引入
课堂探究
思考2 已知任意角α的终边与单位圆相交于点P(x,y),请同学们思考回答点P关于原点、x轴、y轴对称的三个点的坐标分别是什么
点P(x,y)关于原点的对称点P1的坐标是( x, y),
点P(x,y)关于x轴的对称点P2的坐标是(x, y),
点P(x,y)关于y轴的对称点P3的坐标是( x,y).
问题引入
课堂探究
探究一 诱导公式二
如图,角π+α的三角函数值与α的三角函数值之间有什么关系
角π+α与角α的终边关于原点O对称,
sin α=y, sin(π+α)= y,
cos α=x, cos(π+α)= x,
tan α=, tan(π+α)=.
x
y
O
课堂探究
x
y
O
公式二
归纳新知
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
课堂探究
探究二 诱导公式三
如图,角α与 α的三角函数值之间有什么关系
角 α与角α的终边关于x轴对称,
sin α=y, sin( α)= y,
cos α=x, cos( α)=x,
tan α=, tan( α)== .
x
y
O
课堂探究
归纳新知
公式三
x
y
O
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
课堂探究
探究三 诱导公式四
如图,根据上两组公式的推导,你能否推导出角π α与α的三角函数值之间的关系
角π α与角α的终边关于y轴对称,
sin α=y, sin(π α)=y,
cos α=x, cos(π α)= x,
tan α= tan(π α)== .
x
y
O
课堂探究
归纳新知
公式四
x
y
O
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
课堂探究
思考3 诱导公式一、二、三、四有什么规律
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α,
其中,k∈Z.
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
公式一
公式二
公式四
公式三
α+k·2π(k∈Z), α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
函数名不变,符号看象限
课堂探究
例1 求下列三角函数值:
(1)cos 225°; (2)sin;
(3)sin( ); (4)tan( 2 040°).
解 (1)cos 225°=cos(180°+45°)= cos 45°= .
(2)sin=sin(2π+)=sin=sin(π )=sin.
(3)sin( )= sin= sin(5π+)= ( sin)=.
(4)tan( 2 040°)= tan 2 040°= tan(6×360° 120°)=tan 120°=tan(180° 60°)= tan 60°= .
课堂探究
思考4 通过例题,你对诱导公式一、二、三、四有什么进一步的认识 你能归纳把任意角的三角函数化为锐角三角函数的步骤吗
利用公式一~公式四把任意角的三角函数转化为锐角三角函数,一般可按下列步骤进行:
上述步骤体现了由未知转化为已知的转化与化归思想方法.
任意负角的
三角函数
任意正角的
三角函数
的角的三角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
课堂探究
例2 化简:.
解 原式== cos α.
课堂探究
探究四 诱导公式五
如图,作点P(x,y)关于直线y=x的对称点P1(y,x),以OP1为终边的角γ与角α有什么关系 角γ与角α的三角函数值之间有什么关系
γ=2kπ+( α) (k∈Z).
公式五
sin( α)=cos α,
cos( α)=sin α.
课堂探究
探究五 诱导公式六
如图,作点P1(y,x)关于y轴的对称点P2,又能得到什么结论
公式六
sin(+α)=cos α,
cos(+α)= sin α.
课堂探究
思考5 你能概括一下公式五、六的共同特点和规律吗
±α的正弦(余弦)函数值,等于α的余弦(正弦)函数值,
前面加上一个把α看成锐角时原函数值的符号.
课堂探究
思考6 诱导公式可统一为±α(k∈Z)的三角函数与α的三角函数之间的关系,你有什么办法记住这些公式
sin( α)=cos α,
cos( α)=sin α.
sin(+α)=cos α,
cos(+α)= sin α.
sin(α+2kπ)=sin α,
cos(α+2kπ)=cos α,
tan(α+2kπ)=tan α
sin(π+α)= sin α,
cos(π+α)= cos α,
tan(π+α)=tan α.
sin( α)= sin α,
cos( α)=cos α,
tan( α)= tan α.
sin(π α)=sin α,
cos(π α)= cos α,
tan(π α)= tan α.
口诀:奇变偶不变,符号看象限.
课堂探究
口诀的意义:
k·±α(k∈Z)的三角函数值,
(1)当k为偶数时,
等于α的同名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号;
(2)当k为奇数时,
等于α的异名三角函数值,前面加上一个把α看作锐角时原三角函数值的符号.
课堂探究
例3 证明:
(1)sin( α)= cos α;
(2)cos( α)= sin α.
证明 (1)sin( α)=sin= sin( α)= cos α.
(2)cos( α)=cos= cos( α)= sin α.
课堂探究
例4 化简:
.
解 原式=
==
= tan α.
课堂探究
例5 已知sin(53 α)=,且 270<α< 90,求sin(37+α)的值.
解 因为 270<α< 90,所以143<53 α<323.
又因为sin(53 α)>0,
所以143<53 α<180 ,
所以cos(53 α)= ,
所以sin(37+α)=sin[90 (53 α)]=cos(53 α)= .
评价反馈
1. 下列各式不正确的是( )
A.sin(α+180°)= sin α
B.cos( α+β)= cos(α β)
C.sin( α 360°)= sin α
D.cos( α β)=cos(α+β)
B
解析 cos( α+β)=cos [ (α β)]=cos(α β),故B项错误.
评价反馈
2. sin 600°的值为( )
A. B.
C. D.
D
解析 sin 600°=sin(720° 120°)
= sin 120°= sin(180° 60°)
= sin 60°= .
故选D.
评价反馈
3. cos 1 030°= ( )
A.cos 50° B. cos 50°
C.sin 50° D. sin 50°
A
解析 cos 1 030°=cos(3×360° 50°)
=cos( 50°)
=cos 50°.
评价反馈
4. 若sin<0,且cos>0,则θ是 ( )
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
B
解析 因为sin=cos θ<0,
cos=sin θ>0,
所以θ是第二象限角,
故选B.
评价反馈
5. 已知sin φ=,求cos+sin(3π φ)的值.
解 ∵sin φ=,
∴cos=cos(6π +φ)=cos( +φ)=cos( φ)=sin φ=,
∴cos+sin(3π φ)=+sin(π φ)=+sin φ=.
课堂小结
1.诱导公式.
2.诱导公式的记忆.
3.利用诱导公式求任意角的三角函数值的步骤.
我们今天都学习了哪些知识
思考问题
课堂小结
三角函数的简化过程图:
归纳总结
任意负角的
三角函数
任意正角的
三角函数
的角的三角函数
锐角的三角函数
用公式
三或一
用公式一
用公式
二或四
三角函数的简化过程口诀:负化正,正化小,化到锐角为终了.
诱导公式记忆口诀:奇变偶不变,符号看象限.
布置作业
完成教材第194195页习题5.3第4,6题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
