第五章 5.4.1正弦函数、余弦函数的图象--人教A版高中数学必修第一册教学课件(共34张PPT)
文档属性
| 名称 | 第五章 5.4.1正弦函数、余弦函数的图象--人教A版高中数学必修第一册教学课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览








文档简介
(共34张PPT)
5.4.1 正弦函数、
余弦函数的图象
第五章 三角函数
数学
学习目标
①掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的与正弦、余弦有关的函数的图象.
②理解正弦曲线与余弦曲线之间的联系.
学习重难点
重点:
正弦函数、余弦函数的图象.
难点:
正弦函数与余弦函数图象间的关系.
课堂导入
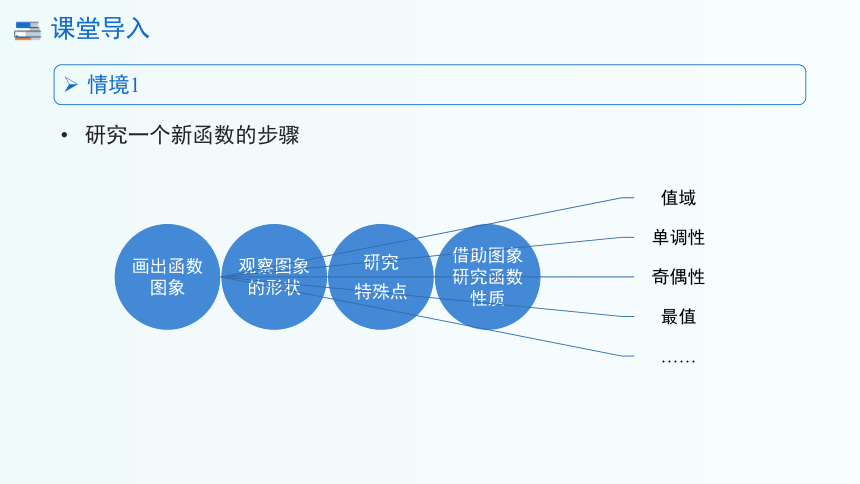
情境1
研究一个新函数的步骤
课堂导入
情境2
回忆我们以前学过的指数函数、对数函数,如何画出它们的图象
列表描点法:列表→描点→连线
请尝试画出当x∈[0,2π]时,y=sin x的图象.
课堂导入
问题
阅读教材第196~199页,思考并完成以下问题.
1.任意角的正弦函数在单位圆中是怎样定义的
2.怎样作出正弦函数y=sin x的图象
3.怎样作出余弦函数y=cos x的图象
4.正弦曲线与余弦曲线的区别与联系.
探究一 正弦、余弦曲线的定义
课堂探究
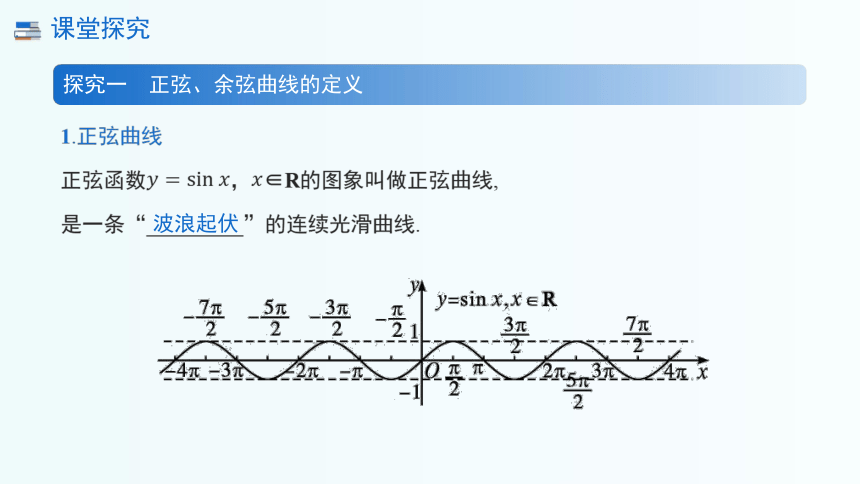
1.正弦曲线
正弦函数,∈R的图象叫做正弦曲线,
是一条“_________”的连续光滑曲线.
波浪起伏
探究一 正弦、余弦曲线的定义
课堂探究
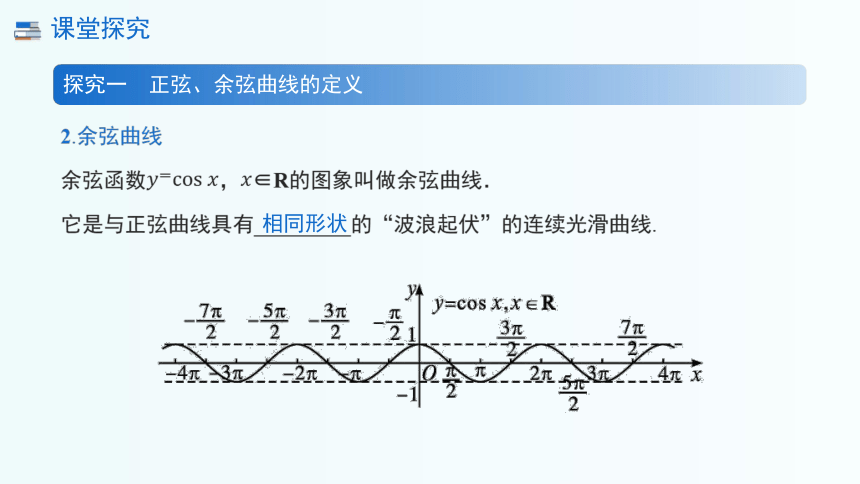
2.余弦曲线
余弦函数,∈R的图象叫做余弦曲线.
它是与正弦曲线具有_________的“波浪起伏”的连续光滑曲线.
相同形状
探究二 “五点法”画图
课堂探究
步骤:
(1)列表
0 π 2π
0 1 0 0
1 0 1 0 1
探究二 “五点法”画图
课堂探究
(2)描点
画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是
,, ,, ;
画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是
,, ,, .
(0,0)
(π,0)
(2π,0)
(0,1)
(π,1)
(2π,1)
探究二 “五点法”画图
课堂探究
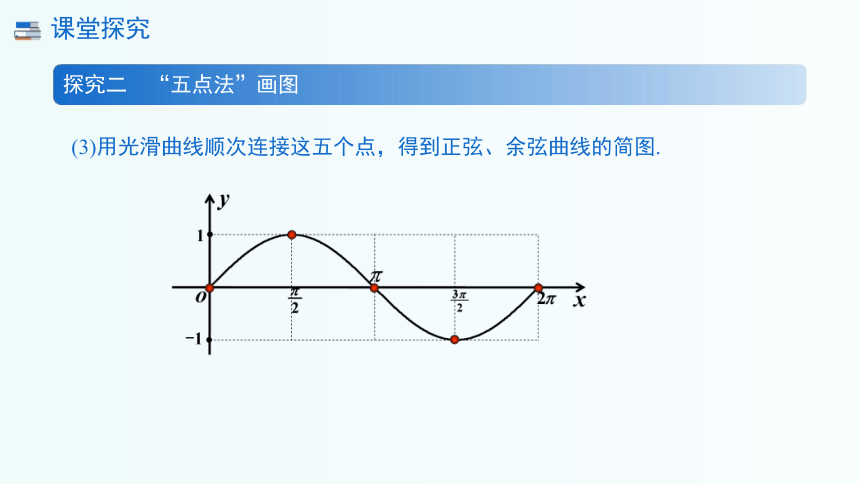
(3)用光滑曲线顺次连接这五个点,得到正弦、余弦曲线的简图.
探究三 正弦、余弦曲线的联系
课堂探究
依据诱导公式cos x=sin,
要得到y=cos x的图象,
只需把y=sin x的图象向 平移 个单位长度即可.
左
课堂探究
x
sinx
1+sinx
0
1
0
1
0
1 2 1 0 1
0 2
解 (1)按五个关键点列表:
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
描点并将它们用光滑的曲线连接起来(如图).
步骤:
1.列表
2.描点
3.连线
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
x 0 π 2π
cosx
1
0
1
0
1
1 0 1 0 1
题型一 作正弦函数、余弦函数的简图
解 (2)按五个关键点列表:
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
描点并将它们用光滑的曲线连接起来(如图).
课堂探究
简单三角函数图象的画法
(1)五点作图法
作正弦曲线、余弦曲线要理解几何法作图,掌握五点法作图.
“五点”即y=sin x或y=cos x的图象在区间 [0,2π] 内的最高点、最低点和与x轴的交点.
(2)图象变换
平移变换、对称变换、翻折变换.
解题技巧
【跟踪训练1】
(1)画出函数y=|sin x|, x∈R的简图.
解 (1)按五个关键点列表:
x
sinx
|sinx|
0
1
0
1
0
0 1 0 1 0
0 2
课堂探究
【跟踪训练1】
描点并将它们用光滑的曲线连接起来(如图).
课堂探究
(1)画出函数y=|sin x|, x∈R的简图.
【跟踪训练1】
解 (2)列表取点如下:
课堂探究
x 0 π
π 2π
f(x) 1 0 0 1
(2)如图,在给定的直角坐标系中,作出函数f(x)=cos在区间[0,π]上的图象.
描点、连线,作出函数f(x)=cos在
区间[0,π]上的图象,如图所示.
课堂探究
【跟踪训练1】
(2)如图,在给定的直角坐标系中,作出函数f(x)=cos在区间[0,π]上的图象.
课堂探究
例2 求函数f(x)=lg sin x+的定义域.
题型二 正弦函数、余弦函数图象的简单应用
解 由题意,得x满足不等式组
作出y=sin x的图象,如图所示.
结合图象可得x∈[ 4, π)∪(0,π).
课堂探究
例3 在同一直角坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断方程
sin x=lg x的解的个数.
题型二 正弦函数、余弦函数图象的简单应用
解 在平面直角坐标系Oxy中分别画出函数y=sin x和y=lg x的图象,如图所示.
由图象可知方程sin x=lg x有3个解.
课堂探究
正弦函数、余弦函数图象的简单应用
(1)解不等式问题
解与三角函数有关的不等式可以借助三角函数图象直观地观察得到,
同时要注意区间端点的取舍.
(2)方程的根(或函数零点)问题
三角函数的图象是研究三角函数的重要工具,通过图象可较简便地解决问题,
这正是数形结合思想方法的应用.
解题技巧
【跟踪训练2】
(1)函数y=的定义域是 .
解析 由题意知,自变量x应满足2sin x 1≥0,
即sin x≥.
由y=sin x在区间[0,2π]上的图象,
可知≤x≤,
所以y=的定义域是,k∈Z.
课堂探究
,k∈Z
【跟踪训练2】
(2)若函数f(x)=sin x 2m-1,x∈[0,2π]有两个零点,求实数m的取值范围.
(2)解 由题意可知,sin x 2m-1=0在区间[0,2π]上有2个根,
即sin x=2m+1在区间[0,2π]上有两个根.
则函数y=sin x, x∈[0,2π]的图象与直线y=2m+1有2个交点.
由函数y=sin x, x∈[0,2π]的图象可知-1<2m+1<1, 且2m+1≠0,
解得-1故m∈
课堂探究
1. 函数y=sin x(x∈R)图象的一条对称轴是( )
A.x轴 B.y轴
C.直线y=x D.直线x=
D
评价反馈
2. 函数y= cos x的图象与余弦函数y=cos x的图象( )
A.只关于x轴对称
B.关于原点对称
C.关于原点、x轴对称
D.关于原点、坐标轴对称
C
3. 若x∈[0,2π],则函数y=的定义域是( )
A.[0,π] B.
C. D.
C
评价反馈
4. 在区间(0,2π)内,使sin x>|cos x|的x的取值范围是( )
A. B.
C. D.
A
5. 利用“五点法”作出下列函数的简图:
(1)y= sin x(0≤x≤2π); (2)y=1+cos x(0≤x≤2π).
评价反馈
解 利用“五点法”作图.
(1)列表:
x 0 π 2π
sin x 0 1 0 0
sin x 0 0 1 0
描点作图,如图所示.
5. 利用“五点法”作出下列函数的简图:
(1)y= sin x(0≤x≤2π); (2)y=1+cos x(0≤x≤2π).
评价反馈
(2)列表:
x 0 π 2π
cos x 1 0 0 1
1+cos x 2 1 0 1 2
描点作图,如图所示.
6. 画出函数y=sin|x|,x∈R的图象.
评价反馈
解 y=sin|x|=
其图象如图所示,
归纳总结
课堂小结
一、简单三角函数图象画法
1.五点作图法.
2.图象变换:
平移变换、对称变换、翻折变换.
二、正弦函数、余弦函数图象的简单应用
1.解不等式问题
结合图象,注意区间端点的取舍.
2.方程的根(或函数零点)问题
数形结合.
布置作业
完成教材第200页练习,第213页习题5.4第1题.
谢谢大家
5.4.1 正弦函数、
余弦函数的图象
第五章 三角函数
数学
学习目标
①掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的与正弦、余弦有关的函数的图象.
②理解正弦曲线与余弦曲线之间的联系.
学习重难点
重点:
正弦函数、余弦函数的图象.
难点:
正弦函数与余弦函数图象间的关系.
课堂导入
情境1
研究一个新函数的步骤
课堂导入
情境2
回忆我们以前学过的指数函数、对数函数,如何画出它们的图象
列表描点法:列表→描点→连线
请尝试画出当x∈[0,2π]时,y=sin x的图象.
课堂导入
问题
阅读教材第196~199页,思考并完成以下问题.
1.任意角的正弦函数在单位圆中是怎样定义的
2.怎样作出正弦函数y=sin x的图象
3.怎样作出余弦函数y=cos x的图象
4.正弦曲线与余弦曲线的区别与联系.
探究一 正弦、余弦曲线的定义
课堂探究
1.正弦曲线
正弦函数,∈R的图象叫做正弦曲线,
是一条“_________”的连续光滑曲线.
波浪起伏
探究一 正弦、余弦曲线的定义
课堂探究
2.余弦曲线
余弦函数,∈R的图象叫做余弦曲线.
它是与正弦曲线具有_________的“波浪起伏”的连续光滑曲线.
相同形状
探究二 “五点法”画图
课堂探究
步骤:
(1)列表
0 π 2π
0 1 0 0
1 0 1 0 1
探究二 “五点法”画图
课堂探究
(2)描点
画正弦函数y=sin x,x∈[0,2π]的图象,五个关键点是
,, ,, ;
画余弦函数y=cos x,x∈[0,2π]的图象,五个关键点是
,, ,, .
(0,0)
(π,0)
(2π,0)
(0,1)
(π,1)
(2π,1)
探究二 “五点法”画图
课堂探究
(3)用光滑曲线顺次连接这五个点,得到正弦、余弦曲线的简图.
探究三 正弦、余弦曲线的联系
课堂探究
依据诱导公式cos x=sin,
要得到y=cos x的图象,
只需把y=sin x的图象向 平移 个单位长度即可.
左
课堂探究
x
sinx
1+sinx
0
1
0
1
0
1 2 1 0 1
0 2
解 (1)按五个关键点列表:
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
描点并将它们用光滑的曲线连接起来(如图).
步骤:
1.列表
2.描点
3.连线
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
x 0 π 2π
cosx
1
0
1
0
1
1 0 1 0 1
题型一 作正弦函数、余弦函数的简图
解 (2)按五个关键点列表:
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
课堂探究
题型一 作正弦函数、余弦函数的简图
例1 画出下列函数的简图:
(1)y=1+sin x,x∈[0,2π]; (2)y= cos x,x∈[0,2π].
描点并将它们用光滑的曲线连接起来(如图).
课堂探究
简单三角函数图象的画法
(1)五点作图法
作正弦曲线、余弦曲线要理解几何法作图,掌握五点法作图.
“五点”即y=sin x或y=cos x的图象在区间 [0,2π] 内的最高点、最低点和与x轴的交点.
(2)图象变换
平移变换、对称变换、翻折变换.
解题技巧
【跟踪训练1】
(1)画出函数y=|sin x|, x∈R的简图.
解 (1)按五个关键点列表:
x
sinx
|sinx|
0
1
0
1
0
0 1 0 1 0
0 2
课堂探究
【跟踪训练1】
描点并将它们用光滑的曲线连接起来(如图).
课堂探究
(1)画出函数y=|sin x|, x∈R的简图.
【跟踪训练1】
解 (2)列表取点如下:
课堂探究
x 0 π
π 2π
f(x) 1 0 0 1
(2)如图,在给定的直角坐标系中,作出函数f(x)=cos在区间[0,π]上的图象.
描点、连线,作出函数f(x)=cos在
区间[0,π]上的图象,如图所示.
课堂探究
【跟踪训练1】
(2)如图,在给定的直角坐标系中,作出函数f(x)=cos在区间[0,π]上的图象.
课堂探究
例2 求函数f(x)=lg sin x+的定义域.
题型二 正弦函数、余弦函数图象的简单应用
解 由题意,得x满足不等式组
作出y=sin x的图象,如图所示.
结合图象可得x∈[ 4, π)∪(0,π).
课堂探究
例3 在同一直角坐标系中,作函数y=sin x和y=lg x的图象,根据图象判断方程
sin x=lg x的解的个数.
题型二 正弦函数、余弦函数图象的简单应用
解 在平面直角坐标系Oxy中分别画出函数y=sin x和y=lg x的图象,如图所示.
由图象可知方程sin x=lg x有3个解.
课堂探究
正弦函数、余弦函数图象的简单应用
(1)解不等式问题
解与三角函数有关的不等式可以借助三角函数图象直观地观察得到,
同时要注意区间端点的取舍.
(2)方程的根(或函数零点)问题
三角函数的图象是研究三角函数的重要工具,通过图象可较简便地解决问题,
这正是数形结合思想方法的应用.
解题技巧
【跟踪训练2】
(1)函数y=的定义域是 .
解析 由题意知,自变量x应满足2sin x 1≥0,
即sin x≥.
由y=sin x在区间[0,2π]上的图象,
可知≤x≤,
所以y=的定义域是,k∈Z.
课堂探究
,k∈Z
【跟踪训练2】
(2)若函数f(x)=sin x 2m-1,x∈[0,2π]有两个零点,求实数m的取值范围.
(2)解 由题意可知,sin x 2m-1=0在区间[0,2π]上有2个根,
即sin x=2m+1在区间[0,2π]上有两个根.
则函数y=sin x, x∈[0,2π]的图象与直线y=2m+1有2个交点.
由函数y=sin x, x∈[0,2π]的图象可知-1<2m+1<1, 且2m+1≠0,
解得-1
课堂探究
1. 函数y=sin x(x∈R)图象的一条对称轴是( )
A.x轴 B.y轴
C.直线y=x D.直线x=
D
评价反馈
2. 函数y= cos x的图象与余弦函数y=cos x的图象( )
A.只关于x轴对称
B.关于原点对称
C.关于原点、x轴对称
D.关于原点、坐标轴对称
C
3. 若x∈[0,2π],则函数y=的定义域是( )
A.[0,π] B.
C. D.
C
评价反馈
4. 在区间(0,2π)内,使sin x>|cos x|的x的取值范围是( )
A. B.
C. D.
A
5. 利用“五点法”作出下列函数的简图:
(1)y= sin x(0≤x≤2π); (2)y=1+cos x(0≤x≤2π).
评价反馈
解 利用“五点法”作图.
(1)列表:
x 0 π 2π
sin x 0 1 0 0
sin x 0 0 1 0
描点作图,如图所示.
5. 利用“五点法”作出下列函数的简图:
(1)y= sin x(0≤x≤2π); (2)y=1+cos x(0≤x≤2π).
评价反馈
(2)列表:
x 0 π 2π
cos x 1 0 0 1
1+cos x 2 1 0 1 2
描点作图,如图所示.
6. 画出函数y=sin|x|,x∈R的图象.
评价反馈
解 y=sin|x|=
其图象如图所示,
归纳总结
课堂小结
一、简单三角函数图象画法
1.五点作图法.
2.图象变换:
平移变换、对称变换、翻折变换.
二、正弦函数、余弦函数图象的简单应用
1.解不等式问题
结合图象,注意区间端点的取舍.
2.方程的根(或函数零点)问题
数形结合.
布置作业
完成教材第200页练习,第213页习题5.4第1题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
