第一章 1.4充分条件与必要条件--人教A版高中数学必修第一册教学课件(共29张PPT)
文档属性
| 名称 | 第一章 1.4充分条件与必要条件--人教A版高中数学必修第一册教学课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
1.4 充分条件和必要条件
第一章 集合与常用逻辑用语
数学
学习目标
①理解充分条件的意义及判定定理的充分条件的关系;理解必要条件的意义及性质定理与必要条件的关系.
②理解充要条件的意义及数学定义与充要条件的关系;初步使用常用逻辑用语进行数学表达、论证和交流,提升逻辑推理素养.
学习重难点
重点:
正确理解充分条件、必要条件及充要条件的概念.
难点:
能正确判断是充分条件、必要条件还是充要条件.
课堂导入
情境1
在初中,我们已经对命题有了初步的认识.
一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.
记p:x>2,q:x>0.
判断命题“若x>2,则x>0”的真假.
“若x>2,则x>0”是真命题.
0
2
1
课堂导入
情境2
下列“若p,则q”形式的命题中,哪些是真命题 哪些是假命题
(1)若平行四边形的对角线互相垂直,则这个平行四边形是菱形;
(2)若两个三角形的周长相等,则这两个三角形全等;
(3)若,则;
(4)若平面内两条直线a和b均垂直于直线l,则a//b.
真
假
假
真
课堂探究
探究一 充分条件与必要条件
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可以推出q,记作p q,并且说,p是q的充分条件,q是p的必要条件.
如果“若p,则q”为假命题,那么由条件p不能推出结论q,记作pq.此时,我们就说p不是q的充分条件,q不是p的必要条件.
课堂探究
探究一 充分条件与必要条件
命题真假 “若p,则q”为真命题 “若p,则q”为假命题
推出关系
条件关系
p q
pq
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
课堂探究
小试牛刀
【例题1】
(1)若四边形的两组对角分别相等,则这个四边形是平行四边形;
(2)若两个三角形的三边成比例,则这两个三角形相似;
(3)若四边形为菱形,则这个四边形的对角线互相垂直;
这是一条平行四边形的判定定理,p q,所以p是q的充分条件.
这是一条相似三角形的判定定理,p q,所以p是q的充分条件.
这是一条菱形的性质定理,p q,所以p是q的充分条件.
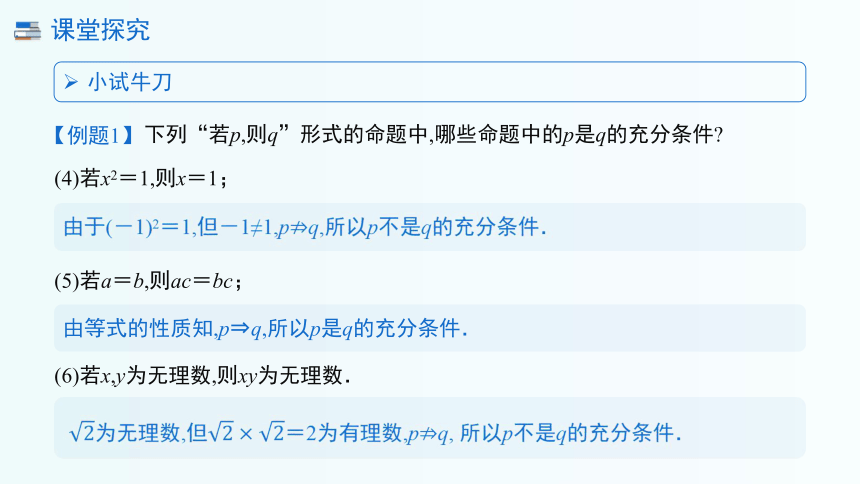
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
课堂探究
小试牛刀
【例题1】
(4)若x2=1,则x=1;
由于(-1)2=1,但-1≠1,pq,所以p不是q的充分条件.
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
(5)若a=b,则ac=bc;
由等式的性质知,p q,所以p是q的充分条件.
(6)若x,y为无理数,则xy为无理数.
为无理数,但=2为有理数,pq, 所以p不是q的充分条件.
思考问题
例1中命题(1)给出了“四边形是平行四边形”的一个充分条件,这样的充分条件唯一吗 若不唯一,那么你能给出不同的充分条件吗
课堂探究
四边形的两组对边分别相等;四边形的一组对边平行且相等;
四边形的两条对角线互相平分.
你能说出几个两条直线平行的充分条件
一般地,数学中的每一条判定定理都给出了相应数学结论成立的一个
充分条件.
课堂探究
小试牛刀
【例题2】
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
(1)若四边形为平行四边形,则这个四边形的两组对角分别相等;
这是一条平行四边形的性质定理,p q,所以q是p的必要条件.
(2)若两个三角形相似,则这两个三角形的三边成比例;
这是一条相似三角形的性质定理,p q,所以q是p的必要条件.
(3)若四边形的对角线互相垂直,则这个四边形是菱形.
如图,四边形ABCD的对角线互相垂直,但它不是菱形,p q,
所以q不是p的必要条件.
课堂探究
小试牛刀
【例题2】
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
(4)若x=1,则x2=1;
显然,p q,所以q不是p的必要条件.
(5)若ac=bc,则a=b;
由于(-1)×0=1×0,但-1≠1,p q,所以q不是p的必要条件.
(6)若xy为无理数,则x,y为无理数.
由于1× 为无理数,但1,不全是无理数,p q,所以q不是p的必要条件.
思考问题
例2中命题(1)给出了“四边形是平行四边形”的一个必要条件,这样的必要条件唯一吗 若不唯一,你能给出几个其它的必要条件吗
课堂探究
四边形的两组对边分别相等;四边形的一组对边平行且相等;
四边形的两条对角线互相平分.
一般地,数学中的每一条性质定理都给出了相应数学结论成立的一个
必要条件.
课堂探究
探究二 充要条件
思考:下列“若p,则q”形式的命题中,哪些命题与它们的逆命题都是真命题
(1)若两个三角形的两角和其中一角所对的边分别相等,则这两个三角形全等;
(2)若两个三角形全等,则这两个三角形的周长相等;
(3)若一元二次方程ax2+bx+c=0有两个不相等的实数根,则ac<0;
(4)若A∪B是空集,则A与B均是空集.
命题(1)、(4)和它们的逆命题都是真命题;
命题(2)是真命题,但它的逆命题是假命题;
命题(3)是假命题,但它的逆命题是真命题.
课堂探究
探究二 充要条件
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即既有p q又有q p,就记作p q.
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件.
显然,如果p是q的充要条件,那么q也是p的充要条件.
课堂探究
小试牛刀
【例题3】
(1)p:四边形是正方形,q:四边形的对角线互相垂直且平分;
下列各题中,哪些p是q的充要条件
因为对角线互相垂直且平分的四边形不一定是正方形,所以q p,所以p不是q的充要条件.
(2)p:两个三角形相似,q:两个三角形三边成比例;
因为“若p,则q”是相似三角形的性质定理,“若q,则p”是相似三角形的判定定理,所以它们均是真命题,即p q,所以p是q的充要条件.
课堂探究
小试牛刀
【例题3】
(3)p:xy>0,q:x>0,y>0;
下列各题中,哪些p是q的充要条件
因为xy>0时,x>0,y>0不一定成立,所以p q,所以p不是q的充要条件.
(4)p:x=1是一元二次方程ax2+bx+c=0的一个根,q:a+b+c=0(a≠0)
因为“若p,则q”与“若q,则p”均为真命题,即p q,所以p是q的充要条件.
思考问题
通过上面的学习,你能给出“四边形是平行四边形”的充要条件吗
课堂探究
四边形的两组对角分别相等;四边形的两组对边分别相等;四边形的一组
对边平行且相等;四边形的对角线互相平分;四边形的两组对边分别平行.
课堂探究
归纳新知
命题 真假 “若p,则q”为真命题 “若p,则q”为假命题 “若p,则q”与逆命题“若q,则p”均为真命题
推出 关系
条件 关系
p q
p是q的充分条件,q是p的必要条件
pq
p q
p不是q的充分条件,q不是p的必要条件
p是q的充要条件,q是p的充要条件
评价反馈
1. 已知以下“若p,则q”形式的命题:
①若p:|x|=|y|,则q:x=y;
②设a,b是实数,若p:a+b>0,则q:ab>0;
③若p:x∈A={x|0④若p:x∈A={x|x=6k,k∈Z},则q:x∈B={x|x=3k,k∈Z}.
其中p是q的充分条件的命题是_______________;p不是q的充分条件的命题是___________;q是p的必要条件的命题是__________;q不是p的必要条件的命题是____________. (填序号)
③④
①②
③④
①②
解析 ①由已知|x|=|y|可能有x=y或x=-y,p q,所以p不是q的充分条件,q不是p的必要条件.
评价反馈
②当a=3,b=-1时,a+b>0,但ab<0,p q,所以p不是q的充分条件,q不是p的必要条件.
③当x∈A时,必有x∈B,p q,所以p是q的充分条件,q是p的必要条件.
④当x∈A时,必有x∈B,p q,所以p是q的充分条件,q是p的必要条件.
综上,p是q的充分条件的命题是③④,p不是q的充分条件的命题是①②,q是p的必要条件的命题是③④,q不是p的必要条件的命题是①②.
②设a,b是实数,若p:a+b>0,则q:ab>0;
③若p:x∈A={x|0④若p:x∈A={x|x=6k,k∈Z},则q:x∈B={x|x=3k,k∈Z}.
评价反馈
2. 若a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析 由a>0且b>0可得a+b>0且ab>0,
由a+b>0有a,b至少一个为正,又ab>0可得a,b同号,两者同时成立,则必有a>0且b>0,故选C.
C
评价反馈
3. 已知p:1-x<0,q: x>a,若p是q的充分不必要条件,则a的取值范围是________.
解析 由题意知p:x>1,q:x>a,若p是q的充分不必要条件,则p q,但q p,
也就是说,p对应集合是q对应集合的真子集,所以a<1.
{a|a<1}
评价反馈
4. 如果集合A={x},B={x|0A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析 因为A={x|0所以m∈A m∈B,但是m∈B m∈A,所以“m∈A”是“m∈B”的充分不必要条件.
故选A.
A
评价反馈
5. 若A是B的充分不必要条件,C是B的必要不充分条件,D是C的充要条件,则D是A的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析 由题意得
B
所以D是A的必要不充分条件,故选B.
课堂小结
1. 充分条件、必要条件、充要条件的概念.
2. 判断充分、必要条件的基本步骤:
①认清条件和结论;
②考察 p q 和 p q 是否能成立.
3. 判别技巧:
① 可先简化命题;
② 否定一个命题只要举出一个反例即可.
课堂小结
充分必要条件
命题
充分必要条件与集合的关系
注意
可以判断真假的陈述句
真命题:判断为真的语句为真命题;判断为假的语句为假命题
小范围可以推出大范围.大范围不可以推出小范围
集合关系
若p q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件 p q且q p
p是q的必要不充分条件 p q且q p
p是q的充要条件 pq
p是q的既不充分也不必要条件 p q且q p 且
布置作业
完成教材第22页练习.
完成教材第22~23页习题1.4.
谢谢大家
1.4 充分条件和必要条件
第一章 集合与常用逻辑用语
数学
学习目标
①理解充分条件的意义及判定定理的充分条件的关系;理解必要条件的意义及性质定理与必要条件的关系.
②理解充要条件的意义及数学定义与充要条件的关系;初步使用常用逻辑用语进行数学表达、论证和交流,提升逻辑推理素养.
学习重难点
重点:
正确理解充分条件、必要条件及充要条件的概念.
难点:
能正确判断是充分条件、必要条件还是充要条件.
课堂导入
情境1
在初中,我们已经对命题有了初步的认识.
一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.
记p:x>2,q:x>0.
判断命题“若x>2,则x>0”的真假.
“若x>2,则x>0”是真命题.
0
2
1
课堂导入
情境2
下列“若p,则q”形式的命题中,哪些是真命题 哪些是假命题
(1)若平行四边形的对角线互相垂直,则这个平行四边形是菱形;
(2)若两个三角形的周长相等,则这两个三角形全等;
(3)若,则;
(4)若平面内两条直线a和b均垂直于直线l,则a//b.
真
假
假
真
课堂探究
探究一 充分条件与必要条件
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由p可以推出q,记作p q,并且说,p是q的充分条件,q是p的必要条件.
如果“若p,则q”为假命题,那么由条件p不能推出结论q,记作pq.此时,我们就说p不是q的充分条件,q不是p的必要条件.
课堂探究
探究一 充分条件与必要条件
命题真假 “若p,则q”为真命题 “若p,则q”为假命题
推出关系
条件关系
p q
pq
p是q的充分条件
q是p的必要条件
p不是q的充分条件
q不是p的必要条件
课堂探究
小试牛刀
【例题1】
(1)若四边形的两组对角分别相等,则这个四边形是平行四边形;
(2)若两个三角形的三边成比例,则这两个三角形相似;
(3)若四边形为菱形,则这个四边形的对角线互相垂直;
这是一条平行四边形的判定定理,p q,所以p是q的充分条件.
这是一条相似三角形的判定定理,p q,所以p是q的充分条件.
这是一条菱形的性质定理,p q,所以p是q的充分条件.
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
课堂探究
小试牛刀
【例题1】
(4)若x2=1,则x=1;
由于(-1)2=1,但-1≠1,pq,所以p不是q的充分条件.
下列“若p,则q”形式的命题中,哪些命题中的p是q的充分条件
(5)若a=b,则ac=bc;
由等式的性质知,p q,所以p是q的充分条件.
(6)若x,y为无理数,则xy为无理数.
为无理数,但=2为有理数,pq, 所以p不是q的充分条件.
思考问题
例1中命题(1)给出了“四边形是平行四边形”的一个充分条件,这样的充分条件唯一吗 若不唯一,那么你能给出不同的充分条件吗
课堂探究
四边形的两组对边分别相等;四边形的一组对边平行且相等;
四边形的两条对角线互相平分.
你能说出几个两条直线平行的充分条件
一般地,数学中的每一条判定定理都给出了相应数学结论成立的一个
充分条件.
课堂探究
小试牛刀
【例题2】
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
(1)若四边形为平行四边形,则这个四边形的两组对角分别相等;
这是一条平行四边形的性质定理,p q,所以q是p的必要条件.
(2)若两个三角形相似,则这两个三角形的三边成比例;
这是一条相似三角形的性质定理,p q,所以q是p的必要条件.
(3)若四边形的对角线互相垂直,则这个四边形是菱形.
如图,四边形ABCD的对角线互相垂直,但它不是菱形,p q,
所以q不是p的必要条件.
课堂探究
小试牛刀
【例题2】
下列“若p,则q”形式的命题中,哪些命题中的q是p的必要条件
(4)若x=1,则x2=1;
显然,p q,所以q不是p的必要条件.
(5)若ac=bc,则a=b;
由于(-1)×0=1×0,但-1≠1,p q,所以q不是p的必要条件.
(6)若xy为无理数,则x,y为无理数.
由于1× 为无理数,但1,不全是无理数,p q,所以q不是p的必要条件.
思考问题
例2中命题(1)给出了“四边形是平行四边形”的一个必要条件,这样的必要条件唯一吗 若不唯一,你能给出几个其它的必要条件吗
课堂探究
四边形的两组对边分别相等;四边形的一组对边平行且相等;
四边形的两条对角线互相平分.
一般地,数学中的每一条性质定理都给出了相应数学结论成立的一个
必要条件.
课堂探究
探究二 充要条件
思考:下列“若p,则q”形式的命题中,哪些命题与它们的逆命题都是真命题
(1)若两个三角形的两角和其中一角所对的边分别相等,则这两个三角形全等;
(2)若两个三角形全等,则这两个三角形的周长相等;
(3)若一元二次方程ax2+bx+c=0有两个不相等的实数根,则ac<0;
(4)若A∪B是空集,则A与B均是空集.
命题(1)、(4)和它们的逆命题都是真命题;
命题(2)是真命题,但它的逆命题是假命题;
命题(3)是假命题,但它的逆命题是真命题.
课堂探究
探究二 充要条件
如果“若p,则q”和它的逆命题“若q,则p”均是真命题,即既有p q又有q p,就记作p q.
此时,p既是q的充分条件,也是q的必要条件,我们说p是q的充分必要条件,简称为充要条件.
显然,如果p是q的充要条件,那么q也是p的充要条件.
课堂探究
小试牛刀
【例题3】
(1)p:四边形是正方形,q:四边形的对角线互相垂直且平分;
下列各题中,哪些p是q的充要条件
因为对角线互相垂直且平分的四边形不一定是正方形,所以q p,所以p不是q的充要条件.
(2)p:两个三角形相似,q:两个三角形三边成比例;
因为“若p,则q”是相似三角形的性质定理,“若q,则p”是相似三角形的判定定理,所以它们均是真命题,即p q,所以p是q的充要条件.
课堂探究
小试牛刀
【例题3】
(3)p:xy>0,q:x>0,y>0;
下列各题中,哪些p是q的充要条件
因为xy>0时,x>0,y>0不一定成立,所以p q,所以p不是q的充要条件.
(4)p:x=1是一元二次方程ax2+bx+c=0的一个根,q:a+b+c=0(a≠0)
因为“若p,则q”与“若q,则p”均为真命题,即p q,所以p是q的充要条件.
思考问题
通过上面的学习,你能给出“四边形是平行四边形”的充要条件吗
课堂探究
四边形的两组对角分别相等;四边形的两组对边分别相等;四边形的一组
对边平行且相等;四边形的对角线互相平分;四边形的两组对边分别平行.
课堂探究
归纳新知
命题 真假 “若p,则q”为真命题 “若p,则q”为假命题 “若p,则q”与逆命题“若q,则p”均为真命题
推出 关系
条件 关系
p q
p是q的充分条件,q是p的必要条件
pq
p q
p不是q的充分条件,q不是p的必要条件
p是q的充要条件,q是p的充要条件
评价反馈
1. 已知以下“若p,则q”形式的命题:
①若p:|x|=|y|,则q:x=y;
②设a,b是实数,若p:a+b>0,则q:ab>0;
③若p:x∈A={x|0
其中p是q的充分条件的命题是_______________;p不是q的充分条件的命题是___________;q是p的必要条件的命题是__________;q不是p的必要条件的命题是____________. (填序号)
③④
①②
③④
①②
解析 ①由已知|x|=|y|可能有x=y或x=-y,p q,所以p不是q的充分条件,q不是p的必要条件.
评价反馈
②当a=3,b=-1时,a+b>0,但ab<0,p q,所以p不是q的充分条件,q不是p的必要条件.
③当x∈A时,必有x∈B,p q,所以p是q的充分条件,q是p的必要条件.
④当x∈A时,必有x∈B,p q,所以p是q的充分条件,q是p的必要条件.
综上,p是q的充分条件的命题是③④,p不是q的充分条件的命题是①②,q是p的必要条件的命题是③④,q不是p的必要条件的命题是①②.
②设a,b是实数,若p:a+b>0,则q:ab>0;
③若p:x∈A={x|0
评价反馈
2. 若a,b是实数,则“a>0且b>0”是“a+b>0且ab>0”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析 由a>0且b>0可得a+b>0且ab>0,
由a+b>0有a,b至少一个为正,又ab>0可得a,b同号,两者同时成立,则必有a>0且b>0,故选C.
C
评价反馈
3. 已知p:1-x<0,q: x>a,若p是q的充分不必要条件,则a的取值范围是________.
解析 由题意知p:x>1,q:x>a,若p是q的充分不必要条件,则p q,但q p,
也就是说,p对应集合是q对应集合的真子集,所以a<1.
{a|a<1}
评价反馈
4. 如果集合A={x},B={x|0
C. 充要条件 D. 既不充分也不必要条件
解析 因为A={x|0
故选A.
A
评价反馈
5. 若A是B的充分不必要条件,C是B的必要不充分条件,D是C的充要条件,则D是A的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
解析 由题意得
B
所以D是A的必要不充分条件,故选B.
课堂小结
1. 充分条件、必要条件、充要条件的概念.
2. 判断充分、必要条件的基本步骤:
①认清条件和结论;
②考察 p q 和 p q 是否能成立.
3. 判别技巧:
① 可先简化命题;
② 否定一个命题只要举出一个反例即可.
课堂小结
充分必要条件
命题
充分必要条件与集合的关系
注意
可以判断真假的陈述句
真命题:判断为真的语句为真命题;判断为假的语句为假命题
小范围可以推出大范围.大范围不可以推出小范围
集合关系
若p q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件 p q且q p
p是q的必要不充分条件 p q且q p
p是q的充要条件 pq
p是q的既不充分也不必要条件 p q且q p 且
布置作业
完成教材第22页练习.
完成教材第22~23页习题1.4.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
