第二章 2.1等式性质与不等式性质第1课时--人教A版高中数学必修第一册教学课件(共32张PPT)
文档属性
| 名称 | 第二章 2.1等式性质与不等式性质第1课时--人教A版高中数学必修第一册教学课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
2.1 等式性质与不等式性质
第1课时
第二章 一元二次函数、方程和不等式
数学
学习目标
①理解各个不等符号的含义.
②会用不等式(组)表示实际问题中的不等关系.
③会用比较法(作差法)比较两实数(式)的大小.
④会用作差法证明不等式.
学习重难点
重点:
应用不等式(组)表示实际问题中的不等关系,比较两实数(式)的大小.
难点:
准确地应用不等式(组)表示实际问题中的不等关系,应用作差法比较两实数(式)大小过程中的变形.
课堂导入
情境1
购买火车票有一项规定:
随同成人旅行,身高超过1.1m(含1.1m)而不超过1.5m的儿童,享受半价客票、加快票和空调票(简称儿童票);超1.5m时应买全价票.
每一成人旅客可免费携带一名身高不足1.1米的儿童,超过一名时,超过的人数应买儿童票.
从数学的角度,应如何理解和表示“不超过”“超过”呢
课堂导入
你能用不等式或不等式组表示下列问题中的不等关系吗
(1)某路段限速40 km/h;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋白质的含量应不少于2.3%;
解 设在该路段行驶的汽车的速度为 km/h,“限速40 km/h”就是的大小不能超过40,于是,.
解 由题意,得
情境2
课堂导入
你能用不等式或不等式组表示下列问题中的不等关系吗
(3)三角形两边之和大于第三边、两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
解 设△ABC的三条边为a,b,c,则a+b>c, ab解 如图,设C是直线AB外的任意一点,CD垂直于AB,垂足为D,E是直线AB上不同于D的任意一点,则CD情境2
探究一 不等式的概念
课堂探究
1.不等式的定义
用不等号表示不等关系的式子,叫做不等式.
我们用数学符号“≠”、“>”、“<”、“≥”、“≤”
连接两个数或代数式,以表示它们之间的不等关系,含有
这些符号的式子,叫做_________.
不等式
课堂探究
2.不等式a≤b和a≥ b的含义
不等式 读作 含义 等价于
a≤b a小于或等于b aa≥b a大于或等于b a>b,或者a=b “a不小于b”,即若a>b与a=b之中有一个正确,则a≥b正确.
探究一 不等式的概念
课堂探究
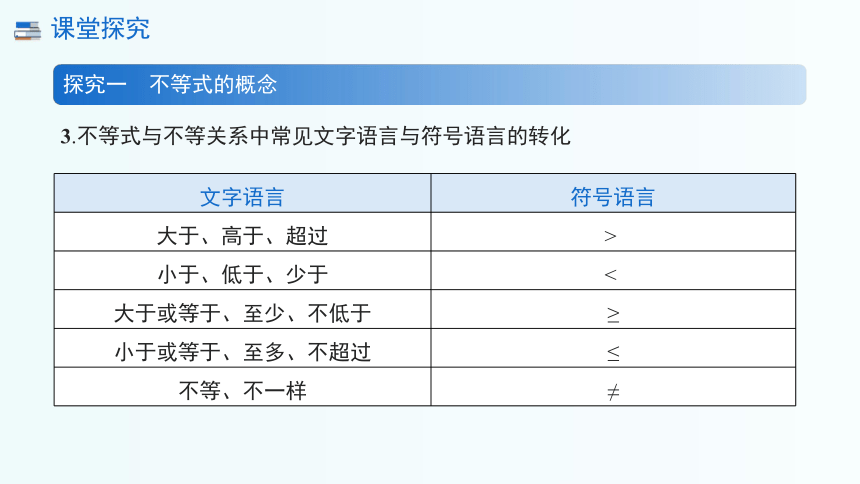
文字语言 符号语言
大于、高于、超过 >
小于、低于、少于 <
大于或等于、至少、不低于 ≥
小于或等于、至多、不超过 ≤
不等、不一样 ≠
3.不等式与不等关系中常见文字语言与符号语言的转化
探究一 不等式的概念
(1)某校对高一美术生划定录取分数线,专业成绩不低于95分,文化课总分高于380分,体育成绩超过45分,用不等式组表示就是( )
A. B. C. D.
课堂探究
【例题1】
解析 因为“不低于”即“≥”, “高于”即“>”, “超过”即“>”,
所以x≥95,y>380,z>45,
所以用不等式组表示为
D
课堂探究
【例题1】
解 提价后销售的总收入为(8-×0.2)x万元,
那么不等关系“销售的总收入不低于20万元”可以表示的不等式为
(8-×0.2)x≥20.
(2)某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,杂志的单价每提高0.1元,销售量就可能减少2 000本.若把提价后每本杂志的定价设为x元,怎样用不等式表示销售的总收入不低于20万元呢
用不等式(组)表示不等关系的解题方法:
归纳新知
课堂探究
探究二 实数的不等关系
课堂探究
设 , 是两个实数,它们在数轴上所对应的点分别是A,B,
当点A在点B的左边时, < ;
当点A在点B的右边时, > ;
当点A和点B重合时, = .
A
B
B
A
A(B)
探究二 实数的不等关系
课堂探究
a>b a-b>0;
a=b a-b=0;
a关于实数a,b大小的比较,有以下基本事实:
如果a-b是正数,那么a>b;如果a-b等于0,那么a=b;如果a-b是负数,那么a这个基本事实可以表示为
探究三 不等式的性质
课堂探究
不等式的性质 文字语言
性质1
性质2
性质3
不等式两边加(或减)同一个数(或式子),不等号的方向不变
不等式的两边同乘(或除以)一个正数,不等号的方向不变
不等式的两边同乘(或除以)一个负数,不等号的方向改变
课堂探究
【例题2】
解 运用作差法:
因为(x+2)(x+3)-(x+1)(x+4)
=(x2+5x+6)-(x2+5x+4)
=2>0,
所以(x+2)(x+3)>(x+1)(x+4).
比较( +2)( +3)和( +1)( +4)的大小.
0是正数与负数的分界线,它为比较实数的大小提供了标杆.
课堂探究
【变式训练1】
解 因为2(x+2)(x+3)-(x+1)(x+4)
=x2+5x+8
=>0,
所以2(x+2)(x+3)>(x+1)(x+4).
比较2(+2)+3)和(+1)(+4)的大小.
课堂探究
【变式训练2】
解 (x+2)(x+3)(2x+4)=x2+3x+2=(x+1)·(x+2),
因为x>1,
所以(x+1)(x+2)>0,所以(x+2)(x+3)>2x+4.
当x>1时,比较(x+2)(x+3)和2x+4的大小.
课堂小结
小结
作差法比较两个实数(式)大小的基本步骤:
课堂小结
小结
注意:
(1)0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
(2)以上基本步骤可概括为“三步一结论”——“判断”是目的,“变形”是关键.
课堂探究
【例题3】
解 设图中直角三角形的两条直角边的长为a,b.
一般地, a,b∈R,有a2+b2≥2ab,
当且仅当a=b时,等号成立.
如图,这是在北京召开的第24届国际数学家大会的会标中的图案,该图案是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出相等关系和不等关系吗
课堂探究
【例题3】
证明 a2+b2-2ab=(a-b)2.
因为 a,b∈R,(a-b)2≥0,当且仅当a=b时,等号成立,所以a2+b2-2ab≥0.
因此,由两个实数大小关系的基本事实,得a2+b2≥2ab,当且仅当a=b时,等号成立.
如图,这是在北京召开的第24届国际数学家大会的会标中的图案,该图案是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.
能用等式或不等式表示你找出的相等关系和不等关系,并证明其成立吗
1. 思考辨析(正确的画“√”,错误的画“×”)
(1)不等式x≥2的含义是指x不小于2. ( )
(2)两个实数a,b之间,有且只有a>b,a=b,a(3)不等式5≥3是正确的. ( )
√
√
√
2. 雷电的温度大约是28 000 ℃,比太阳表面温度的4.5倍还要高.如果太阳表面温度为t ℃,那么t应满足的关系式是 .
4.5t<28000
解析 由题意得太阳表面温度的4.5倍小于雷电的温度,即4.5t<28000.
3. 有如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形.从图形上确定这两个广告牌面积的大小关系,并将这种关系用含字母a,b(a≠b)的不等式表示出来( )
A.(a2+b2)>ab B.(a2+b2)C.(a2+b2)≥ab D.(a2+b2)≤ab
A
解析 图(1)是由两个等腰直角三角形构成的,面积S1=a2+b2,
图(2)是一个矩形,面积S2=ab,可得a2+b2)>ab(a≠b).故选A.
4. 若M=a2,N=-a-1,则M,N的大小关系为 .
M >N
解析 M-N=a2+a+1=(a+2+>0,
所以M>N.
5. 若x∈R,试比较3x2+6x与4x2 2x+16的大小.
解 因为(3x2+6x)-(4x2-2x+16)=-x2+8x-16=-(x-4)2≤0,
当x=4时,等号成立,
所以3x2+6x≤4x2-2x+16.
6. 若x∈R,试比较a=与b=的大小关系.
解 因为a-b=≥0,
当x=1时,等号成立.
所以a≥b.
7. 已知a=x2+2,b=2x,求证:a>b.
证明 因为a-b=x2-2x+2=(x-1)2+1>0,
所以a>b,得证.
课堂小结
小结
1.基础知识归纳
(1)不等式的概念及各不等号的含义;
(2)用不等式(组)表示不等关系;
(3)应用比较两实数大小的基本事实比较数或式的大小.
2.思想方法总结:数形结合思想、作差法.
3.误区警示:忽视不等式中等号成立的条件;作差法中变形不彻底.
布置作业
1.认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
2.预习不等式的性质.
谢谢大家
2.1 等式性质与不等式性质
第1课时
第二章 一元二次函数、方程和不等式
数学
学习目标
①理解各个不等符号的含义.
②会用不等式(组)表示实际问题中的不等关系.
③会用比较法(作差法)比较两实数(式)的大小.
④会用作差法证明不等式.
学习重难点
重点:
应用不等式(组)表示实际问题中的不等关系,比较两实数(式)的大小.
难点:
准确地应用不等式(组)表示实际问题中的不等关系,应用作差法比较两实数(式)大小过程中的变形.
课堂导入
情境1
购买火车票有一项规定:
随同成人旅行,身高超过1.1m(含1.1m)而不超过1.5m的儿童,享受半价客票、加快票和空调票(简称儿童票);超1.5m时应买全价票.
每一成人旅客可免费携带一名身高不足1.1米的儿童,超过一名时,超过的人数应买儿童票.
从数学的角度,应如何理解和表示“不超过”“超过”呢
课堂导入
你能用不等式或不等式组表示下列问题中的不等关系吗
(1)某路段限速40 km/h;
(2)某品牌酸奶的质量检查规定,酸奶中脂肪的含量应不少于2.5%,蛋白质的含量应不少于2.3%;
解 设在该路段行驶的汽车的速度为 km/h,“限速40 km/h”就是的大小不能超过40,于是,.
解 由题意,得
情境2
课堂导入
你能用不等式或不等式组表示下列问题中的不等关系吗
(3)三角形两边之和大于第三边、两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
解 设△ABC的三条边为a,b,c,则a+b>c, ab
探究一 不等式的概念
课堂探究
1.不等式的定义
用不等号表示不等关系的式子,叫做不等式.
我们用数学符号“≠”、“>”、“<”、“≥”、“≤”
连接两个数或代数式,以表示它们之间的不等关系,含有
这些符号的式子,叫做_________.
不等式
课堂探究
2.不等式a≤b和a≥ b的含义
不等式 读作 含义 等价于
a≤b a小于或等于b a
探究一 不等式的概念
课堂探究
文字语言 符号语言
大于、高于、超过 >
小于、低于、少于 <
大于或等于、至少、不低于 ≥
小于或等于、至多、不超过 ≤
不等、不一样 ≠
3.不等式与不等关系中常见文字语言与符号语言的转化
探究一 不等式的概念
(1)某校对高一美术生划定录取分数线,专业成绩不低于95分,文化课总分高于380分,体育成绩超过45分,用不等式组表示就是( )
A. B. C. D.
课堂探究
【例题1】
解析 因为“不低于”即“≥”, “高于”即“>”, “超过”即“>”,
所以x≥95,y>380,z>45,
所以用不等式组表示为
D
课堂探究
【例题1】
解 提价后销售的总收入为(8-×0.2)x万元,
那么不等关系“销售的总收入不低于20万元”可以表示的不等式为
(8-×0.2)x≥20.
(2)某种杂志原以每本2.5元的价格销售,可以售出8万本.据市场调查,杂志的单价每提高0.1元,销售量就可能减少2 000本.若把提价后每本杂志的定价设为x元,怎样用不等式表示销售的总收入不低于20万元呢
用不等式(组)表示不等关系的解题方法:
归纳新知
课堂探究
探究二 实数的不等关系
课堂探究
设 , 是两个实数,它们在数轴上所对应的点分别是A,B,
当点A在点B的左边时, < ;
当点A在点B的右边时, > ;
当点A和点B重合时, = .
A
B
B
A
A(B)
探究二 实数的不等关系
课堂探究
a>b a-b>0;
a=b a-b=0;
a关于实数a,b大小的比较,有以下基本事实:
如果a-b是正数,那么a>b;如果a-b等于0,那么a=b;如果a-b是负数,那么a
探究三 不等式的性质
课堂探究
不等式的性质 文字语言
性质1
性质2
性质3
不等式两边加(或减)同一个数(或式子),不等号的方向不变
不等式的两边同乘(或除以)一个正数,不等号的方向不变
不等式的两边同乘(或除以)一个负数,不等号的方向改变
课堂探究
【例题2】
解 运用作差法:
因为(x+2)(x+3)-(x+1)(x+4)
=(x2+5x+6)-(x2+5x+4)
=2>0,
所以(x+2)(x+3)>(x+1)(x+4).
比较( +2)( +3)和( +1)( +4)的大小.
0是正数与负数的分界线,它为比较实数的大小提供了标杆.
课堂探究
【变式训练1】
解 因为2(x+2)(x+3)-(x+1)(x+4)
=x2+5x+8
=>0,
所以2(x+2)(x+3)>(x+1)(x+4).
比较2(+2)+3)和(+1)(+4)的大小.
课堂探究
【变式训练2】
解 (x+2)(x+3)(2x+4)=x2+3x+2=(x+1)·(x+2),
因为x>1,
所以(x+1)(x+2)>0,所以(x+2)(x+3)>2x+4.
当x>1时,比较(x+2)(x+3)和2x+4的大小.
课堂小结
小结
作差法比较两个实数(式)大小的基本步骤:
课堂小结
小结
注意:
(1)0是正数与负数的分界点,它为实数比较大小提供了“标杆”.
(2)以上基本步骤可概括为“三步一结论”——“判断”是目的,“变形”是关键.
课堂探究
【例题3】
解 设图中直角三角形的两条直角边的长为a,b.
一般地, a,b∈R,有a2+b2≥2ab,
当且仅当a=b时,等号成立.
如图,这是在北京召开的第24届国际数学家大会的会标中的图案,该图案是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出相等关系和不等关系吗
课堂探究
【例题3】
证明 a2+b2-2ab=(a-b)2.
因为 a,b∈R,(a-b)2≥0,当且仅当a=b时,等号成立,所以a2+b2-2ab≥0.
因此,由两个实数大小关系的基本事实,得a2+b2≥2ab,当且仅当a=b时,等号成立.
如图,这是在北京召开的第24届国际数学家大会的会标中的图案,该图案是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.
能用等式或不等式表示你找出的相等关系和不等关系,并证明其成立吗
1. 思考辨析(正确的画“√”,错误的画“×”)
(1)不等式x≥2的含义是指x不小于2. ( )
(2)两个实数a,b之间,有且只有a>b,a=b,a
√
√
√
2. 雷电的温度大约是28 000 ℃,比太阳表面温度的4.5倍还要高.如果太阳表面温度为t ℃,那么t应满足的关系式是 .
4.5t<28000
解析 由题意得太阳表面温度的4.5倍小于雷电的温度,即4.5t<28000.
3. 有如图所示的两种广告牌,其中图(1)是由两个等腰直角三角形构成的,图(2)是一个矩形.从图形上确定这两个广告牌面积的大小关系,并将这种关系用含字母a,b(a≠b)的不等式表示出来( )
A.(a2+b2)>ab B.(a2+b2)
A
解析 图(1)是由两个等腰直角三角形构成的,面积S1=a2+b2,
图(2)是一个矩形,面积S2=ab,可得a2+b2)>ab(a≠b).故选A.
4. 若M=a2,N=-a-1,则M,N的大小关系为 .
M >N
解析 M-N=a2+a+1=(a+2+>0,
所以M>N.
5. 若x∈R,试比较3x2+6x与4x2 2x+16的大小.
解 因为(3x2+6x)-(4x2-2x+16)=-x2+8x-16=-(x-4)2≤0,
当x=4时,等号成立,
所以3x2+6x≤4x2-2x+16.
6. 若x∈R,试比较a=与b=的大小关系.
解 因为a-b=≥0,
当x=1时,等号成立.
所以a≥b.
7. 已知a=x2+2,b=2x,求证:a>b.
证明 因为a-b=x2-2x+2=(x-1)2+1>0,
所以a>b,得证.
课堂小结
小结
1.基础知识归纳
(1)不等式的概念及各不等号的含义;
(2)用不等式(组)表示不等关系;
(3)应用比较两实数大小的基本事实比较数或式的大小.
2.思想方法总结:数形结合思想、作差法.
3.误区警示:忽视不等式中等号成立的条件;作差法中变形不彻底.
布置作业
1.认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
2.预习不等式的性质.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
