第一章 集合与常用逻辑用语 本章小结--人教A版高中数学必修第一册教学课件(共32张PPT)
文档属性
| 名称 | 第一章 集合与常用逻辑用语 本章小结--人教A版高中数学必修第一册教学课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
本章小结
第一章 集合与常用逻辑用语
数学
学习目标
①能够在现实情境中,概括出数学对象的一般特征,并用集合语言予以表达.
②初步学会用三种语言(自然语言、图形语言、符号语言)表达数学研究对象,并能进行转换.
③掌握集合的基本关系与基本运算.
⑤重点提升数学抽象、逻辑推理、数学运算等素养.
④能够借助常用逻辑用语进行数学表达、论证和交流,体会常用逻辑用语在数学中的作用.
学习重难点
重点:
集合的关系与运算,常用逻辑用语.
难点:
已知两个集合间的关系求参数以及充分条件、必要条件的应用.
课堂导入
易错闯关
1.(多选题)下列结论错误的是( )
A
B.若则或
C.对于任意两个集合A,B,关系(A∩B) (A∪B)恒成立
D.含有n个元素的集合有2n个真子集
ABD
2.(多选题)下列结论错误的是( )
A.若已知p:x>1和q:x≥1,则p是q的充分不必要条件
B.“长方形的对角线相等”是存在量词命题
C.当q是p的必要条件时,p是q的充分条件
D.
BD
课堂导入
易错闯关
3.若集合A={x| 3A∪B= .
4.若命题p: a∈R,一次函数y=x+a的图象经过原点,则
p: ;是 命题(填“真”或“假”).
a∈R,一次函数y=x+a的图象不经过原点
假
课堂探究
考点一 集合间的基本关系
元素与集合
1.集合中元素的三个特性:①_______、② _______ 、③ _______ .
2.集合中元素与集合的关系
元素与集合之间的关系有④ _____和⑤ _______两种,表示符号为⑥ ___和⑦ ___.
互异性
确定性
无序性
属于
不属于
∈
课堂探究
考点一 集合间的基本关系
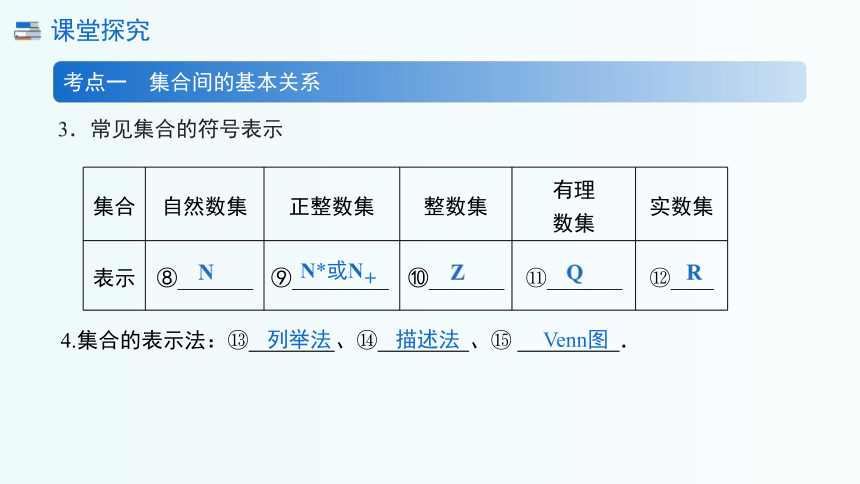
3.常见集合的符号表示
集合 自然数集 正整数集 整数集 有理 数集 实数集
表示 ⑧_______ ⑨_________ ⑩_______ _______ ____
N*或N+
4.集合的表示法: 、 、 .
列举法
描述法
Venn图
课堂探究
考点一 集合间的基本关系
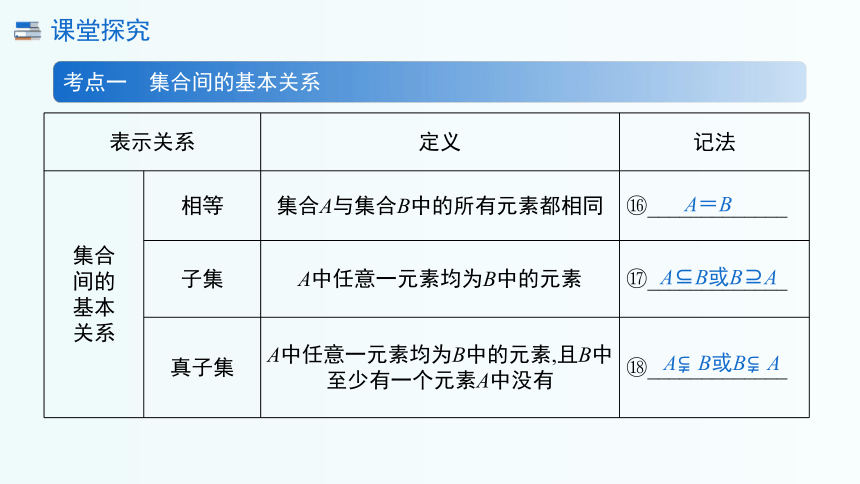
表示关系 定义 记法
集合 间的 基本 关系 相等 集合A与集合B中的所有元素都相同 _____________
子集 A中任意一元素均为B中的元素 _____________
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有 _____________
A=B
A B或B A
A B或B A
空集 空集是任何集合的子集 _____________
空集是任何 ________的真子集 _____________
课堂探究
考点一 集合间的基本关系
非空集合
B(B≠ )
课堂探究
考点一 集合间的基本关系
【例题1】
已知集合,若,则实数的取值范围是( )
A B.
C D
解析 在数轴上标出A,B两集合如图所示,
结合数轴知,若A B,则a≥4.
C
课堂探究
归纳总结
集合间的基本关系的关键点
(1):空集是任何集合的子集,在涉及集合关系时必须优先考虑空集的情况,否则会造成漏解.
(2)端点值:已知两集合间的关系求参数的取值范围时,关键是将条件转化为集合间的关系,进而转化为参数所满足的条件,常用数轴解决此类问题,解答时要注意端点值的取舍.
课堂探究
考点二 集合的基本运算
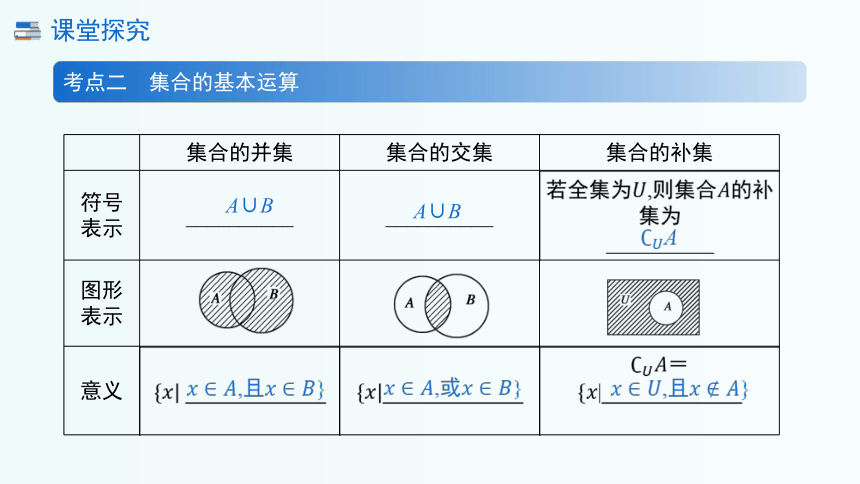
集合的并集 集合的交集 集合的补集
符号 表示 __________ __________
图形 表示
意义
A∪B
A
A∪B
,或}
,且}
,且}
课堂探究
考点二 集合的基本运算
性质
A B
A
A
A B
A
(A)∩ (B)
(A)∪(B)
A
课堂探究
考点二 集合的基本运算
【例题2】
设全集,为实数.
(1)分别求A∩B,A∪(B);
(2)若B∩C=C,求a的取值范围.
解 (1)因为A={x|1≤x≤3},B={x|2所以A∩B={x|2课堂探究
考点二 集合的基本运算
【例题2】
(1)分别求A∩B,A∪(B);
(2)若B∩C=C,求a的取值范围.
解 (2)因为B∩C=C,所以C B,因为B={x|2若C=,则a+1所以所以2故a的取值范围为{a|2设全集,为实数.
课堂探究
归纳总结
集合的基本运算的关注点
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
课堂探究
集合关系和运算中的参数问题
根据集合间关系求参数范围时,要深刻理解子集的概念,把形如A B的问题转化为A B或A=B,进而列出不等式组,使问题得以解决.在建立不等式过程中,可借助数轴以形促数,化抽象为具体.要注意作图准确,分类全面.
课堂探究
考点三 数形结合在集合的基本运算中的应用
【例题3】
已知集合M={(x,y)|y=},N={(x,y)|y=x+b}且M∩N=,求实数b的取值范围.
解 点集M是一个半圆弧,点集N是随b变化的一组平行直线.
,两点集M与N无公共点,
由图象可知,直线在与外侧(不包括,)时,满足,.
课堂探究
考点四 全称量词命题与存在量词命题
【例题4】
判断下列命题是全称量词命题还是存在量词命题,请写出它们的否定,并判断其真假:
解 (1)由于命题中含有全称量词“任意的”,该命题是全称量词命题,所以其否定为“ x∈R,使x2+x+1=0”.
因为Δ= 3<0,所以方程x2+x+1=0无实数解,此命题为假命题.
(2)由于命题中含有存在量词“ ”,该命题是存在量词命题,所以其否定为“ x∈R,有x2+3x+5>0”.
因为Δ= 11<0,所以 x∈R,x2+3x+5>0成立,此命题是真命题.
(1)p:对任意的x∈R,x2+x+1≠0都成立;
(2)q: x∈R,使x2+3x+5≤0.
课堂探究
归纳总结
对全称量词命题和存在量词命题否定的步骤和方法
(1)确定类型:是存在量词命题还是全称量词命题;
(2)改变量词:把全称量词换为恰当的存在量词,把存在量词换为恰当的全称量词;
(3)否定结论:原命题中“是”“有”“存在”“成立”等改为“不是”“没有”“不存在”“不成立”等.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
解 (1),
.
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
解 (2)∵命题“若x=2且y=6,则x+y=8”是真命题,即 q p,∴p q;
命题“若x+y=8,则x=2且y=6”是假命题,即 p q,∴q p.
故p是q的充分不必要条件.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
解 (3)取A=120°,B=30°,p q;取A=30°,B=120°,q p.
故p是q的既不充分也不必要条件.
课堂探究
归纳总结
1.命题按条件和结论的充分性、必要性可分为四类:
(1)充分不必要条件,即,而.
(2)必要不充分条件,即,而.
(3)充要条件,既有,又有.
(4)既不充分也不必要条件,既有,又有.
课堂探究
归纳总结
2.充分条件与必要条件的判断.
(1)直接利用定义判断:即“若成立,则是的充分条件,是的必要条件”.(条件与结论是相对的)
(2)利用等价命题的关系判断:“”的等价命题是“”即“若”成立,则是的充分条件,是的必要条件.
(3)利用集合间的包含关系进行判断:如果条件p和结论q都是集合,那么若,则是的充分条件;若,则是的必要条件;若,则是的充要条件.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
解 若选择①,即x∈P是x∈S的充分不必要条件,
则1m≤1+m且(两个等号不同时成立),解得m≥3,
故实数m的取值范围是{m|m≥3}.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
解 若选择②,即x∈P是x∈S的必要不充分条件.
则1 m≤1+m且两个等号不同时成立),解得m=0.
综上,实数m=0.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
解 若选择③,即x∈P是x∈S的充要条件,
则P=S,即无解,则不存在实数m,使x∈P是x∈S的充要条件.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
课堂探究
归纳总结
1.充分条件、必要条件的应用,一般表现在参数问题的求解上,解题时需注意:
把充分条件、必要条件或充要条件转化为集合之间的关系,根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
2.要注意端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.
课堂小结
布置作业
完成教材第34~35页复习参考题1.
谢谢大家
本章小结
第一章 集合与常用逻辑用语
数学
学习目标
①能够在现实情境中,概括出数学对象的一般特征,并用集合语言予以表达.
②初步学会用三种语言(自然语言、图形语言、符号语言)表达数学研究对象,并能进行转换.
③掌握集合的基本关系与基本运算.
⑤重点提升数学抽象、逻辑推理、数学运算等素养.
④能够借助常用逻辑用语进行数学表达、论证和交流,体会常用逻辑用语在数学中的作用.
学习重难点
重点:
集合的关系与运算,常用逻辑用语.
难点:
已知两个集合间的关系求参数以及充分条件、必要条件的应用.
课堂导入
易错闯关
1.(多选题)下列结论错误的是( )
A
B.若则或
C.对于任意两个集合A,B,关系(A∩B) (A∪B)恒成立
D.含有n个元素的集合有2n个真子集
ABD
2.(多选题)下列结论错误的是( )
A.若已知p:x>1和q:x≥1,则p是q的充分不必要条件
B.“长方形的对角线相等”是存在量词命题
C.当q是p的必要条件时,p是q的充分条件
D.
BD
课堂导入
易错闯关
3.若集合A={x| 3
4.若命题p: a∈R,一次函数y=x+a的图象经过原点,则
p: ;是 命题(填“真”或“假”).
a∈R,一次函数y=x+a的图象不经过原点
假
课堂探究
考点一 集合间的基本关系
元素与集合
1.集合中元素的三个特性:①_______、② _______ 、③ _______ .
2.集合中元素与集合的关系
元素与集合之间的关系有④ _____和⑤ _______两种,表示符号为⑥ ___和⑦ ___.
互异性
确定性
无序性
属于
不属于
∈
课堂探究
考点一 集合间的基本关系
3.常见集合的符号表示
集合 自然数集 正整数集 整数集 有理 数集 实数集
表示 ⑧_______ ⑨_________ ⑩_______ _______ ____
N*或N+
4.集合的表示法: 、 、 .
列举法
描述法
Venn图
课堂探究
考点一 集合间的基本关系
表示关系 定义 记法
集合 间的 基本 关系 相等 集合A与集合B中的所有元素都相同 _____________
子集 A中任意一元素均为B中的元素 _____________
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有 _____________
A=B
A B或B A
A B或B A
空集 空集是任何集合的子集 _____________
空集是任何 ________的真子集 _____________
课堂探究
考点一 集合间的基本关系
非空集合
B(B≠ )
课堂探究
考点一 集合间的基本关系
【例题1】
已知集合,若,则实数的取值范围是( )
A B.
C D
解析 在数轴上标出A,B两集合如图所示,
结合数轴知,若A B,则a≥4.
C
课堂探究
归纳总结
集合间的基本关系的关键点
(1):空集是任何集合的子集,在涉及集合关系时必须优先考虑空集的情况,否则会造成漏解.
(2)端点值:已知两集合间的关系求参数的取值范围时,关键是将条件转化为集合间的关系,进而转化为参数所满足的条件,常用数轴解决此类问题,解答时要注意端点值的取舍.
课堂探究
考点二 集合的基本运算
集合的并集 集合的交集 集合的补集
符号 表示 __________ __________
图形 表示
意义
A∪B
A
A∪B
,或}
,且}
,且}
课堂探究
考点二 集合的基本运算
性质
A B
A
A
A B
A
(A)∩ (B)
(A)∪(B)
A
课堂探究
考点二 集合的基本运算
【例题2】
设全集,为实数.
(1)分别求A∩B,A∪(B);
(2)若B∩C=C,求a的取值范围.
解 (1)因为A={x|1≤x≤3},B={x|2
考点二 集合的基本运算
【例题2】
(1)分别求A∩B,A∪(B);
(2)若B∩C=C,求a的取值范围.
解 (2)因为B∩C=C,所以C B,因为B={x|2
课堂探究
归纳总结
集合的基本运算的关注点
(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.
(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.
(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn图.
课堂探究
集合关系和运算中的参数问题
根据集合间关系求参数范围时,要深刻理解子集的概念,把形如A B的问题转化为A B或A=B,进而列出不等式组,使问题得以解决.在建立不等式过程中,可借助数轴以形促数,化抽象为具体.要注意作图准确,分类全面.
课堂探究
考点三 数形结合在集合的基本运算中的应用
【例题3】
已知集合M={(x,y)|y=},N={(x,y)|y=x+b}且M∩N=,求实数b的取值范围.
解 点集M是一个半圆弧,点集N是随b变化的一组平行直线.
,两点集M与N无公共点,
由图象可知,直线在与外侧(不包括,)时,满足,.
课堂探究
考点四 全称量词命题与存在量词命题
【例题4】
判断下列命题是全称量词命题还是存在量词命题,请写出它们的否定,并判断其真假:
解 (1)由于命题中含有全称量词“任意的”,该命题是全称量词命题,所以其否定为“ x∈R,使x2+x+1=0”.
因为Δ= 3<0,所以方程x2+x+1=0无实数解,此命题为假命题.
(2)由于命题中含有存在量词“ ”,该命题是存在量词命题,所以其否定为“ x∈R,有x2+3x+5>0”.
因为Δ= 11<0,所以 x∈R,x2+3x+5>0成立,此命题是真命题.
(1)p:对任意的x∈R,x2+x+1≠0都成立;
(2)q: x∈R,使x2+3x+5≤0.
课堂探究
归纳总结
对全称量词命题和存在量词命题否定的步骤和方法
(1)确定类型:是存在量词命题还是全称量词命题;
(2)改变量词:把全称量词换为恰当的存在量词,把存在量词换为恰当的全称量词;
(3)否定结论:原命题中“是”“有”“存在”“成立”等改为“不是”“没有”“不存在”“不成立”等.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
解 (1),
.
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
解 (2)∵命题“若x=2且y=6,则x+y=8”是真命题,即 q p,∴p q;
命题“若x+y=8,则x=2且y=6”是假命题,即 p q,∴q p.
故p是q的充分不必要条件.
课堂探究
考点五 充要条件的判断
【例题5】
指出下列各组命题中,是的什么条件(在“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中选一种作答).
(1)在△ABC中,p:∠A+∠C=2∠B,q:∠B=60°;
(2)对于实数x,y,p:x+y≠8,q:x≠2或y≠6;
(3)在△ABC中,p:sin A>sin B,q:tan A>tan B.
解 (3)取A=120°,B=30°,p q;取A=30°,B=120°,q p.
故p是q的既不充分也不必要条件.
课堂探究
归纳总结
1.命题按条件和结论的充分性、必要性可分为四类:
(1)充分不必要条件,即,而.
(2)必要不充分条件,即,而.
(3)充要条件,既有,又有.
(4)既不充分也不必要条件,既有,又有.
课堂探究
归纳总结
2.充分条件与必要条件的判断.
(1)直接利用定义判断:即“若成立,则是的充分条件,是的必要条件”.(条件与结论是相对的)
(2)利用等价命题的关系判断:“”的等价命题是“”即“若”成立,则是的充分条件,是的必要条件.
(3)利用集合间的包含关系进行判断:如果条件p和结论q都是集合,那么若,则是的充分条件;若,则是的必要条件;若,则是的充要条件.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
解 若选择①,即x∈P是x∈S的充分不必要条件,
则1m≤1+m且(两个等号不同时成立),解得m≥3,
故实数m的取值范围是{m|m≥3}.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
解 若选择②,即x∈P是x∈S的必要不充分条件.
则1 m≤1+m且两个等号不同时成立),解得m=0.
综上,实数m=0.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
课堂探究
考点六 充分条件与必要条件的应用
【例题6】
解 若选择③,即x∈P是x∈S的充要条件,
则P=S,即无解,则不存在实数m,使x∈P是x∈S的充要条件.
请从如下三个条件选择一个条件补充到上面的横线上:①充分不必要条件;②必要不充分条件;③充要条件.
已知集合,,且是否存在实数使得是的___________.若存在实数,求出的取值范围;若不存在,请说明理由.
课堂探究
归纳总结
1.充分条件、必要条件的应用,一般表现在参数问题的求解上,解题时需注意:
把充分条件、必要条件或充要条件转化为集合之间的关系,根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
2.要注意端点值的检验.尤其是利用两个集合之间的关系求解参数的取值范围时,不等式是否能够取等号决定端点值的取舍,处理不当容易出现漏解或增解的现象.
课堂小结
布置作业
完成教材第34~35页复习参考题1.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
