第二章 2.1等式性质与不等式性质第2课时--人教A版高中数学必修第一册教学课件(共28张PPT)
文档属性
| 名称 | 第二章 2.1等式性质与不等式性质第2课时--人教A版高中数学必修第一册教学课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:26:25 | ||
图片预览








文档简介
(共28张PPT)
2.1 等式性质与不等式性质
第2课时
第二章 一元二次函数、方程和不等式
数学
学习目标
①通过回忆和再现初中所学的等式性质,寻找共性和差异进一步探究不等式的基本性质.
②理解不等式的基本性质,会用不等式的基本性质解决有关问题.
重点:
不等式的基本性质,等式与不等式的共性与差异.
难点:
类比等式的基本性质及其蕴含的思想方法,研究不等式的基本性质;利用不等式的基本性质证明不等式.
学习重难点
课堂导入
复习情境
不等式与等式都是对大小关系的刻画,所以要想知道不等式有哪些基本性质,可以从等式的性质及其研究方法中获得启发.
那么等式有哪些性质呢
我比你大三岁
那再过三年,我就比你大了
生活中会出现这样的情况吗
课堂探究
探究一 等式的基本性质
★【对称性】如果,那么;
★【传递性】如果,,那么;
★【加减性】如果,那么;
★【同乘性】如果,那么;
★【同除性】如果,,那么.
相等关系自身的特性.
从运算的角度提出的,反映了等式在运算中可保持的不变性.
思考1:你能把等式的基本性质分一下类吗
课堂探究
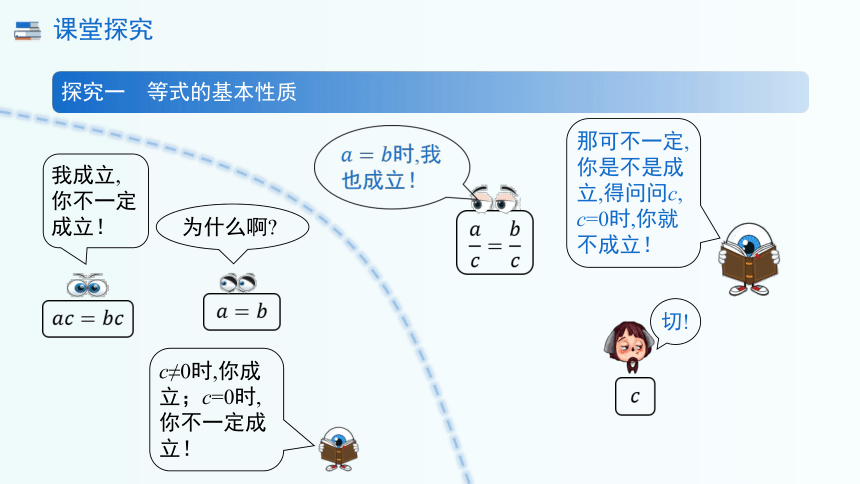
探究一 等式的基本性质
我成立,你不一定成立!
为什么啊
c≠0时,你成立;c=0时,你不一定成立!
时,我也成立!
那可不一定,你是不是成立,得问问c,c=0时,你就不成立!
切!
课堂探究
(多选题)下列运用等式性质进行的变形中,正确的是( )
A. 如果a=b,那么a+c=b c
B. 如果,那么a=b
C. 如果ac=bc,那么a=b
D. 如果a=b,b=c,c=d,那么a=d
小试牛刀
解析 选项A,由等式的性质,得如果a=b,那么a+c=b+c成立,而a+c=b c只有当c等于0时才成立,不正确;B正确;选项C,当c=0时不一定成立,不正确;选项D,如果a=b,b=c,c=d,那么a=d,正确.故选BD.
BD
课堂探究
【例题1】
若3a=5b(,则通过正确的等式变形不能得到的是( )
A. B. 2a=5ba
C. 3a5b=0 D.
A
课堂探究
探究二 不等式的基本性质
★【对称性】如果,那么.即.
★【传递性】如果,,那么.即,.
证明 .
.
如果传递的时候两个不等式只有一个带等号,那么等号是传递不过去的.只有两个不等式都带等号,等号才能传递过去.
例如:
如果且,那么只能得到,无法得到;
如果且,那么只能得到,无法得到;
如果且,那么可以得到,此时有.
课堂探究
探究二 不等式的基本性质
★【可加性】如果,那么 .
不等式两边同时加上一个数,不变号.
证明 如图,把数轴上的两个点A与B同时沿相同方向移动相等的距离,得到另两个点A1与B1,A与B和A1与B1的左右位置关系不会改变.用不等式的语言表示,就是上述性质.
课堂探究
探究二 不等式的基本性质
★【可乘性】如果,,那么;
不等式两边同时乘上一个正数,不变号;
如果,,那么.
不等式两边同时乘上一个负数,要变号.
移项法则:由【可加性】可得,a+b>c a+b+( b)>c+( b) a>c b.
这表明,不等式中任何一项可以改变符号后移到不等号的另一边.
课堂探究
小试牛刀
【例题2】
若a,b,c∈R,则下列命题正确的是( )
A.若a>b,则ac2>bc2 B.若,则a>b
C.若a>b,c>b,则a>c D.若a> b,则c a解析 选项A,若c=0,则A不成立;
选项B,若c<0,则B不成立;
选项C,若a=4,b=2,c=5,显然不成立;
选项D,若a> b,则 aD
课堂探究
探究二 不等式的基本性质
★【同向可加性】如果,,那么;
如果,,那么;
如果,,那么.
★【同向同正可乘性】如果, ,那么.
★【同正可乘方性】如果,那么.
★【同正数开平方性】如果a>b>0,那么.
只有一个等式有等号也是传递不过去的.
我的等号左右能对应加减乘除(除数不为0),你行吗
等式
我只有同向可加性,同向可乘还必须保证是正数!
不等式
课堂探究
小试牛刀
【例题3】
下列命题为真命题的是( )
A.若ac>bc,则a>b B.若a2>b2,则a>b
C.若,则a解析 由ac>bc,当c<0时,有a若a2>b2,不一定有a>b,如( 3)2>( 2)2, 3< 2,选项B不符合题意;
若,不一定有a ,2> 3,选项C不符合题意;
若,则(2<(2,即aD
课堂探究
学以致用——求范围
【例题4】
已知1解 因为1即 7又因为,所以=2,
即<2,即的取值范围.
课堂探究
学以致用——求范围
【小结】
求含字母的数(或式子)的取值范围时的注意事项:
1. 注意题设中的条件;
2. 要正确使用不等式的性质:
(1)两个同方向的不等式可加不可减;
(2)两个正的同向不等式可乘不可除.
课堂探究
【跟踪训练1】
已知≤α<β≤,求满足的取值范围.
解 ∵≤α<β≤,∴,,
两式相加,得,即的取值范围为.
又,∴≤,
∴,又知α<β,∴<0.
故<0,即的取值范围为.
课堂探究
证明不等式
已知c>a>b>0,求证:.
证明 ∵c>a>b>0,∴ca>0,cb>0.
∵a>b>0,∴,又c>0,∴,
∴,又c-a>0,c-b>0,∴.
【例题5】
课堂探究
【小结】
1. 利用不等式性质解决此类问题,一定要理解、记忆不等式性质并注意在解题中灵活、准确地加以应用.
2. 应用不等式的性质进行推导时,注意:
(1)紧扣不等式的性质成立的条件;
(2)不可省略条件或跳步推导;
(3)不能随意构造性质与法则.
3. 倒数原则:①a>b>0 ;②b课堂探究
【跟踪训练2】
已知a>b>0,c(1);(2).
证明 (1)∵c ∴c>d>0.
∵a>b>0,
∴ac>bd>0,
∴0<.
又e<0,
∴.
(2)∵cd>0.
又a>b>0,∴ac>bd>0.
∴(ac)2>(bd)2>0.
两边同乘,得.
又e<0,∴.
1. 若a>b>0,cA. B. C. D.
评价反馈
解析 (方法1)∵cd>0,∴>0.
又a>b>0,∴,∴.
(方法2)令a=3,b=2,c=3,d=2,
则=1,=1,排除选项A,B.
∵==,∴,排除选项C.
D
2. 如果a>b>0,c>d>0,那么下列不等式中不正确的是( )
A. ad>bc B. < C. a+d>b+c D. ac>bd
评价反馈
解析 由已知及不等式的性质可得a+c>b+d,
即ad>bc,所以A正确;
由c>d>0,得>0,又a>b>0,所以,<,即B正确;
显然D正确,因此不正确的选项是C.
C
3. 若1<α<β<1,则下列各式中恒成立的是( )
A.2<αβ<0 B.2<αβ<1
C.1<αβ<0 D.1<αβ<1
评价反馈
解析 由1<α<1,1<β<1,得1<β<1,2<αβ<2,但α<β,
可知2<αβ<0.故选A.
A
4. 能说明“若a>b,则”为假命题的一组a,b的值依次为 .
(答案不唯一)
评价反馈
解析“若a>b,则”是真命题,则ab>0,因此举例只需使得“ab>0” 不成立且a>b即可.
5. 已知a,b,x,y都是正数,且,x>y,求证:.
评价反馈
证明 ∵a,b,x,y都是正数,且,x>y,
∴>0,∴0<,
∴+1<+1,即0<,
∴.
课堂小结
1. 基础知识归纳
(1)等式的基本性质;
(2)不等式的基本性质.
在应用不等式性质时,一定搞清他们的成立前提条件,不可强化或者弱化成立条件.
2. 思想方法总结:数形结合思想、类比法.
3. 误区警示:忽视不等式基本性质中的条件;混淆不等式的基本性质.
4. 要注意“箭头”是单项还是双向的,也就是说每条性质是否具有可逆性.
布置作业
认真整理本节所讲,梳理知识脉络,完成学案.
谢谢大家
2.1 等式性质与不等式性质
第2课时
第二章 一元二次函数、方程和不等式
数学
学习目标
①通过回忆和再现初中所学的等式性质,寻找共性和差异进一步探究不等式的基本性质.
②理解不等式的基本性质,会用不等式的基本性质解决有关问题.
重点:
不等式的基本性质,等式与不等式的共性与差异.
难点:
类比等式的基本性质及其蕴含的思想方法,研究不等式的基本性质;利用不等式的基本性质证明不等式.
学习重难点
课堂导入
复习情境
不等式与等式都是对大小关系的刻画,所以要想知道不等式有哪些基本性质,可以从等式的性质及其研究方法中获得启发.
那么等式有哪些性质呢
我比你大三岁
那再过三年,我就比你大了
生活中会出现这样的情况吗
课堂探究
探究一 等式的基本性质
★【对称性】如果,那么;
★【传递性】如果,,那么;
★【加减性】如果,那么;
★【同乘性】如果,那么;
★【同除性】如果,,那么.
相等关系自身的特性.
从运算的角度提出的,反映了等式在运算中可保持的不变性.
思考1:你能把等式的基本性质分一下类吗
课堂探究
探究一 等式的基本性质
我成立,你不一定成立!
为什么啊
c≠0时,你成立;c=0时,你不一定成立!
时,我也成立!
那可不一定,你是不是成立,得问问c,c=0时,你就不成立!
切!
课堂探究
(多选题)下列运用等式性质进行的变形中,正确的是( )
A. 如果a=b,那么a+c=b c
B. 如果,那么a=b
C. 如果ac=bc,那么a=b
D. 如果a=b,b=c,c=d,那么a=d
小试牛刀
解析 选项A,由等式的性质,得如果a=b,那么a+c=b+c成立,而a+c=b c只有当c等于0时才成立,不正确;B正确;选项C,当c=0时不一定成立,不正确;选项D,如果a=b,b=c,c=d,那么a=d,正确.故选BD.
BD
课堂探究
【例题1】
若3a=5b(,则通过正确的等式变形不能得到的是( )
A. B. 2a=5ba
C. 3a5b=0 D.
A
课堂探究
探究二 不等式的基本性质
★【对称性】如果,那么.即.
★【传递性】如果,,那么.即,.
证明 .
.
如果传递的时候两个不等式只有一个带等号,那么等号是传递不过去的.只有两个不等式都带等号,等号才能传递过去.
例如:
如果且,那么只能得到,无法得到;
如果且,那么只能得到,无法得到;
如果且,那么可以得到,此时有.
课堂探究
探究二 不等式的基本性质
★【可加性】如果,那么 .
不等式两边同时加上一个数,不变号.
证明 如图,把数轴上的两个点A与B同时沿相同方向移动相等的距离,得到另两个点A1与B1,A与B和A1与B1的左右位置关系不会改变.用不等式的语言表示,就是上述性质.
课堂探究
探究二 不等式的基本性质
★【可乘性】如果,,那么;
不等式两边同时乘上一个正数,不变号;
如果,,那么.
不等式两边同时乘上一个负数,要变号.
移项法则:由【可加性】可得,a+b>c a+b+( b)>c+( b) a>c b.
这表明,不等式中任何一项可以改变符号后移到不等号的另一边.
课堂探究
小试牛刀
【例题2】
若a,b,c∈R,则下列命题正确的是( )
A.若a>b,则ac2>bc2 B.若,则a>b
C.若a>b,c>b,则a>c D.若a> b,则c a
选项B,若c<0,则B不成立;
选项C,若a=4,b=2,c=5,显然不成立;
选项D,若a> b,则 a
课堂探究
探究二 不等式的基本性质
★【同向可加性】如果,,那么;
如果,,那么;
如果,,那么.
★【同向同正可乘性】如果, ,那么.
★【同正可乘方性】如果,那么.
★【同正数开平方性】如果a>b>0,那么.
只有一个等式有等号也是传递不过去的.
我的等号左右能对应加减乘除(除数不为0),你行吗
等式
我只有同向可加性,同向可乘还必须保证是正数!
不等式
课堂探究
小试牛刀
【例题3】
下列命题为真命题的是( )
A.若ac>bc,则a>b B.若a2>b2,则a>b
C.若,则a解析 由ac>bc,当c<0时,有a
若,不一定有a
若,则(2<(2,即a
课堂探究
学以致用——求范围
【例题4】
已知1
即<2,即的取值范围.
课堂探究
学以致用——求范围
【小结】
求含字母的数(或式子)的取值范围时的注意事项:
1. 注意题设中的条件;
2. 要正确使用不等式的性质:
(1)两个同方向的不等式可加不可减;
(2)两个正的同向不等式可乘不可除.
课堂探究
【跟踪训练1】
已知≤α<β≤,求满足的取值范围.
解 ∵≤α<β≤,∴,,
两式相加,得,即的取值范围为.
又,∴≤,
∴,又知α<β,∴<0.
故<0,即的取值范围为.
课堂探究
证明不等式
已知c>a>b>0,求证:.
证明 ∵c>a>b>0,∴ca>0,cb>0.
∵a>b>0,∴,又c>0,∴,
∴,又c-a>0,c-b>0,∴.
【例题5】
课堂探究
【小结】
1. 利用不等式性质解决此类问题,一定要理解、记忆不等式性质并注意在解题中灵活、准确地加以应用.
2. 应用不等式的性质进行推导时,注意:
(1)紧扣不等式的性质成立的条件;
(2)不可省略条件或跳步推导;
(3)不能随意构造性质与法则.
3. 倒数原则:①a>b>0 ;②b
【跟踪训练2】
已知a>b>0,c
证明 (1)∵c
∵a>b>0,
∴ac>bd>0,
∴0<.
又e<0,
∴.
(2)∵c
又a>b>0,∴ac>bd>0.
∴(ac)2>(bd)2>0.
两边同乘,得.
又e<0,∴.
1. 若a>b>0,c
评价反馈
解析 (方法1)∵c
又a>b>0,∴,∴.
(方法2)令a=3,b=2,c=3,d=2,
则=1,=1,排除选项A,B.
∵==,∴,排除选项C.
D
2. 如果a>b>0,c>d>0,那么下列不等式中不正确的是( )
A. ad>bc B. < C. a+d>b+c D. ac>bd
评价反馈
解析 由已知及不等式的性质可得a+c>b+d,
即ad>bc,所以A正确;
由c>d>0,得>0,又a>b>0,所以,<,即B正确;
显然D正确,因此不正确的选项是C.
C
3. 若1<α<β<1,则下列各式中恒成立的是( )
A.2<αβ<0 B.2<αβ<1
C.1<αβ<0 D.1<αβ<1
评价反馈
解析 由1<α<1,1<β<1,得1<β<1,2<αβ<2,但α<β,
可知2<αβ<0.故选A.
A
4. 能说明“若a>b,则”为假命题的一组a,b的值依次为 .
(答案不唯一)
评价反馈
解析“若a>b,则”是真命题,则ab>0,因此举例只需使得“ab>0” 不成立且a>b即可.
5. 已知a,b,x,y都是正数,且,x>y,求证:.
评价反馈
证明 ∵a,b,x,y都是正数,且,x>y,
∴>0,∴0<,
∴+1<+1,即0<,
∴.
课堂小结
1. 基础知识归纳
(1)等式的基本性质;
(2)不等式的基本性质.
在应用不等式性质时,一定搞清他们的成立前提条件,不可强化或者弱化成立条件.
2. 思想方法总结:数形结合思想、类比法.
3. 误区警示:忽视不等式基本性质中的条件;混淆不等式的基本性质.
4. 要注意“箭头”是单项还是双向的,也就是说每条性质是否具有可逆性.
布置作业
认真整理本节所讲,梳理知识脉络,完成学案.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
