第二章 2.2基本不等式--人教A版高中数学必修第一册教学课件(共43张PPT)
文档属性
| 名称 | 第二章 2.2基本不等式--人教A版高中数学必修第一册教学课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 00:00:00 | ||
图片预览











文档简介
(共43张PPT)
2.2 基本不等式
第二章 一元二次函数、方程和不等式
数学
学习目标
①理解基本不等式以及使用基本不等式的条件.
②结合具体实例,会用基本不等式解决简单的最值问题.
学习重难点
重点:
基本不等式的定义、证明方法和几何解释,用基本不等式解决简单的最值问题.
难点:
基本不等式的几何解释,用基本不等式解决简单的最值问题.
课堂导入
2002年在北京召开的第24届国际数学家大会会标
思考1:这图案中含有怎样的几何图形
思考2:你能发现图案中的相等关系或不等关系吗
情境1
课堂导入
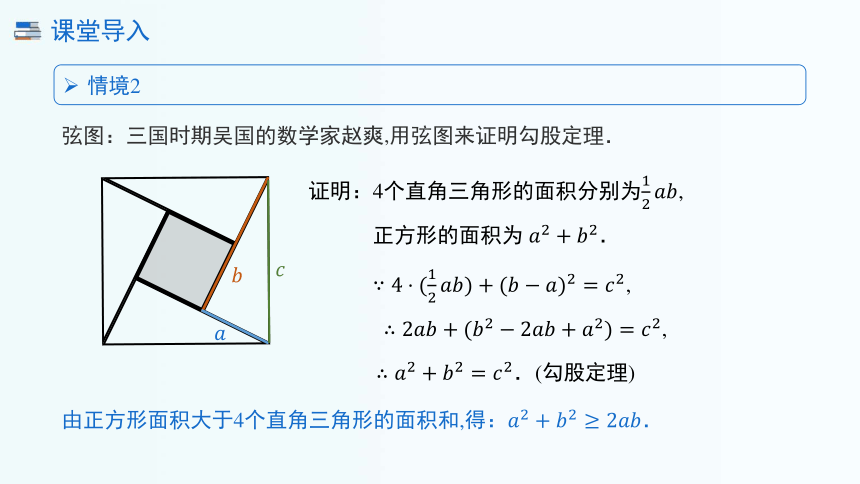
弦图:三国时期吴国的数学家赵爽,用弦图来证明勾股定理.
证明:4个直角三角形的面积分别为,
正方形的面积为 .
,
,
.(勾股定理)
情境2
由正方形面积大于4个直角三角形的面积和,得:.
课堂导入
情境2
对于, R,有,当且仅当时,等号成立.
不等式恒等变形:
, R,有,当且仅当时,等号成立.
, R,有,当且仅当时,等号成立.
不等式特殊变形:
如果,,用和分别代替上式中的,可得 ,当且仅当时,等号成立.
课堂探究
探究一 基本不等式
1. 算术平均数与几何平均数
对于正数,通常称叫做的算术平均数,
叫做的几何平均数.
课堂探究
探究一 基本不等式
2. 基本不等式
当时,有,(1)
当且仅当时,等号成立.
通常称不等式(1)为基本不等式.
基本不等式表明:
两个正数的算术平均数不小于它们的几何平均数.
课堂探究
探究二 基本不等式的条件
思考1 基本不等式中的只能是具体的数吗
提示 既可以是具体的数,也可以是代数式,只要满足就可以.
思考2 基本不等式的叙述中,“正数”二字能省略吗
提示 不能.如时,基本不等式不成立.
思考3 “当且仅当时,等号成立”的含义是什么
提示 当时,
课堂探究
探究三 基本不等式的证明
证明:因为,都是正数,
所以≥0,
即,当且仅当( ,即时,等号成立.
思考4 你能证明基本不等式成立吗
比较法
课堂探究
探究三 基本不等式的证明
证明:要证,
只要证,
要证上式,只要证,
要证上式,只要证,
要证上式,只要证,
显然,成立,当且仅当a=b时,等号成立.
思考4 你能证明基本不等式成立吗
分析法
课堂探究
探究三 基本不等式的证明
证明:因为,
所以2,
所以,即,
当且仅当(,即时,等号成立.
思考4 你能证明基本不等式成立吗
综合法
课堂探究
探究四 基本不等式的变形
①根据不等式的性质可以变形如下:
若则当且仅当时,等号成立.
②根据不等式的可乘方性可以变形如下:
若则,当且仅当时,等号成立.
课堂探究
探究五 基本不等式的几何解释
在右图中,是圆的直径,是上一点,.
过点C作垂直于的弦,连接,.
你能利用这个图形,得出基本不等式的几何解释吗
可证,因此.
由于小于或等于圆的半径,
所以用不等式表示为:.
显然,当且仅当点与圆心重合,即当时,等号成立.
基本不等式的几何意义:在同一个圆中,半径不小于半弦.
A.①② B.①③ C.②③ D.①②③
给出下面三个推导过程:
①为正实数,,当且仅当时,等号成立;
②R,,,当且仅当时,等号成立;
③,∈R,,,当且仅当时,等号成立.
其中正确的推导为( )
课堂探究
【练习】
B
解析 ①,为正实数,,为正实数,符合基本不等式的条件,故①的推导正确;
②∈R,,不符合基本不等式的条件,推导是错误的;
A.①② B.①③ C.②③ D.①②③
给出下面三个推导过程:
①为正实数,,当且仅当时,等号成立;
②R,,,当且仅当时,等号成立;
③,∈R,,,当且仅当时,等号成立.
其中正确的推导为( )
课堂探究
【练习】
B
解析 ③由,得,均为负数,但在推导过程中将整体提取负号后,, 均变为正数,符合基本不等式的条件,故③正确.
A. B.
C. D.
(1)比较大小
【例题1】若,则下列不等式一定成立的是( )
课堂探究
C
解析 (方法1 直接法)
∵,∴,∴.
∵,∴,∴ .
故.故选C.
A. B.
C. D.
课堂探究
解析 (方法2 特值法)
∵,
∴取则排除A,B,D.
故选C.
(1)比较大小
【例题1】若,则下列不等式一定成立的是( )
C
课堂探究
【小结】
运用基本不等式判断所给的不等关系是否正确时,一般有两种处理方法:
(1)若基本不等式成立,进行合理的变形推导.
(2)选取合适的特殊值,举反例排除.注意,特殊值法只能作排除使用,不能作不等式成立的依据.
【跟踪训练1】
设则四个数中最小的是 .
课堂探究
解析 (方法1)因为所以.
又因为所以<1,得
综上,最小.
(方法2)取则所以最小.
课堂探究
证明 因为
所以
所以
当且仅当即时等号成立.
(2)证明不等式
【例题2】已知,求证:.
课堂探究
【小结】
证明不等式的注意点:
(1)基本不等式使用的条件:等号成立的条件是
(2)注意等号成立的条件要一致,若不一致则等号取不到.
(3)注意不等式性质使用的正确性.
【跟踪训练2】
已知是全不相等的正数,求证:.
课堂探究
证明 ∵都是正数,
∴等号成立的条件为.
等号成立的条件为.
两式相乘,得
等号成立的条件为且.
又全不相等,
故.
课堂探究
提示 本题可拓展为当时,,当且仅当,即时,等号成立.
(3)求最值
【例题3】已知,求的最小值.
解析 因为,所以,
当且仅当,即时,等号成立,
的最小值是.
课堂探究
【小结】
已知都是正数,
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值.
可简记为“积定和最小,和定积最大”.
【跟踪训练3】
(1)已知求的最小值;
课堂探究
解 ∵,∴,
当且仅当,即时,等号成立.
故的最小值为
【跟踪训练3】
(2)已知,且求的最大值;
课堂探究
解 ∵,且,
∴由基本不等式,得,
当且仅当时,取到最大值.
∴的最大值为.
【跟踪训练3】
(3)已知求的最大值;
课堂探究
解 ∵ ,
∴,
∴,
当且仅当,即时,等号成立.
故当时,
【跟踪训练3】
(4)已知,求的最大值.
课堂探究
解 ∵
∴
∴
当且仅当
即时,等号成立.
故当时,.
【例题4】(1)用篱笆围成一个面积为100m的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少
课堂探究
A
B
D
C
课堂探究
解 设矩形菜园的长为m,宽为m,则,篱笆的长为m.
,
,
∴,
结论1:两个正变量积为定值,则和有最小值,当且仅当两变量值相等时取最值.简记“积定和最小”.
【例题4】(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少
课堂探究
A
B
D
C
课堂探究
解 设矩形菜园的长为 m,宽为 m,则.
矩形菜园的面积为
,
.
结论2:两个正变量和为定值,则积有最大值,当且仅当两变量值相等时取最值.简记“和定积最大”.
【跟踪训练4】
某游泳馆拟建一个平面图形为矩形且面积为200 m2的泳池,池的深度为1 m,池的四周墙壁建造单价为每米400元,中间一条横向的隔壁建造单价为每米100元,池底建造单价为每平方米60元(池壁厚忽略不计),则泳池的长设计为多少米时,可使总造价最低
课堂探究
解 设泳池的长为 m则宽为 m总造价为元则总造价
整理得到
且仅当时等号成立即泳池的长设计为m时可使总造价最低.
1. 不等式中等号成立的条件是( )
A. B.
C. D.
评价反馈
解析 由基本不等式知等号成立的条件为,即舍去).故选C.
C
2. (1)若,则的最大值为 .
(2)若且则的最大值为 .
评价反馈
解析 (1)(方法1)∵,∴.
∴· 2=,
当且仅当即时,等号成立.
∴当时,取得最大值.
2. (1)若,则的最大值为 .
(2)若且则的最大值为 .
评价反馈
(方法2)∵,∴.
∴ ) ≤3· (,
当且仅当即时,等号成立.
∴当时,取得最大值.
(2)∵∴解得当且仅当时,等号成立.
3. 已知求证:.
评价反馈
证明 ∵
∴当且仅当时,等号成立,,当且仅当时,等号成立,,当且仅当时,等号成立.
∴,即,当且仅当时,等号成立.
4. 某养殖公司欲将一批冷鲜肉用冷藏汽车从甲地运往相距120 km的乙地,运费为每小时60元,装卸费为1000元,冷鲜肉在运输途中的损耗费(单位:元)是汽车速度值(单位:km/h)的2倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)写出运输的总费用(单位:元)与汽车速度(单位:km/h)的函数关系式,并求汽车速度为50 km/h时运输的总费用.
(2)求汽车行驶速度为何值时,运输的总费用最小,最小值为多少
评价反馈
评价反馈
解 (1),
当汽车速度为50 km/h时,运输总费用为(元).
(2)由(1)得,当,即时,等号成立.
故汽车行驶速度为60 km/h时,运输的总费用最小,最小值为1240元.
课堂小结
1.基础知识归纳
(1)基本不等式及其证明、几何解释;
(2)基本不等式的应用,尤其是利用基本不等式求最值.
2.思想方法总结:转化与化归思想
3.误区警示:忽视基本不等式使用前提以及等号成立的条件;利用基本不等式求最值时忽略“一正,二定,三相等”.
布置作业
认真整理本节知识脉络,完成学案.
谢谢大家
2.2 基本不等式
第二章 一元二次函数、方程和不等式
数学
学习目标
①理解基本不等式以及使用基本不等式的条件.
②结合具体实例,会用基本不等式解决简单的最值问题.
学习重难点
重点:
基本不等式的定义、证明方法和几何解释,用基本不等式解决简单的最值问题.
难点:
基本不等式的几何解释,用基本不等式解决简单的最值问题.
课堂导入
2002年在北京召开的第24届国际数学家大会会标
思考1:这图案中含有怎样的几何图形
思考2:你能发现图案中的相等关系或不等关系吗
情境1
课堂导入
弦图:三国时期吴国的数学家赵爽,用弦图来证明勾股定理.
证明:4个直角三角形的面积分别为,
正方形的面积为 .
,
,
.(勾股定理)
情境2
由正方形面积大于4个直角三角形的面积和,得:.
课堂导入
情境2
对于, R,有,当且仅当时,等号成立.
不等式恒等变形:
, R,有,当且仅当时,等号成立.
, R,有,当且仅当时,等号成立.
不等式特殊变形:
如果,,用和分别代替上式中的,可得 ,当且仅当时,等号成立.
课堂探究
探究一 基本不等式
1. 算术平均数与几何平均数
对于正数,通常称叫做的算术平均数,
叫做的几何平均数.
课堂探究
探究一 基本不等式
2. 基本不等式
当时,有,(1)
当且仅当时,等号成立.
通常称不等式(1)为基本不等式.
基本不等式表明:
两个正数的算术平均数不小于它们的几何平均数.
课堂探究
探究二 基本不等式的条件
思考1 基本不等式中的只能是具体的数吗
提示 既可以是具体的数,也可以是代数式,只要满足就可以.
思考2 基本不等式的叙述中,“正数”二字能省略吗
提示 不能.如时,基本不等式不成立.
思考3 “当且仅当时,等号成立”的含义是什么
提示 当时,
课堂探究
探究三 基本不等式的证明
证明:因为,都是正数,
所以≥0,
即,当且仅当( ,即时,等号成立.
思考4 你能证明基本不等式成立吗
比较法
课堂探究
探究三 基本不等式的证明
证明:要证,
只要证,
要证上式,只要证,
要证上式,只要证,
要证上式,只要证,
显然,成立,当且仅当a=b时,等号成立.
思考4 你能证明基本不等式成立吗
分析法
课堂探究
探究三 基本不等式的证明
证明:因为,
所以2,
所以,即,
当且仅当(,即时,等号成立.
思考4 你能证明基本不等式成立吗
综合法
课堂探究
探究四 基本不等式的变形
①根据不等式的性质可以变形如下:
若则当且仅当时,等号成立.
②根据不等式的可乘方性可以变形如下:
若则,当且仅当时,等号成立.
课堂探究
探究五 基本不等式的几何解释
在右图中,是圆的直径,是上一点,.
过点C作垂直于的弦,连接,.
你能利用这个图形,得出基本不等式的几何解释吗
可证,因此.
由于小于或等于圆的半径,
所以用不等式表示为:.
显然,当且仅当点与圆心重合,即当时,等号成立.
基本不等式的几何意义:在同一个圆中,半径不小于半弦.
A.①② B.①③ C.②③ D.①②③
给出下面三个推导过程:
①为正实数,,当且仅当时,等号成立;
②R,,,当且仅当时,等号成立;
③,∈R,,,当且仅当时,等号成立.
其中正确的推导为( )
课堂探究
【练习】
B
解析 ①,为正实数,,为正实数,符合基本不等式的条件,故①的推导正确;
②∈R,,不符合基本不等式的条件,推导是错误的;
A.①② B.①③ C.②③ D.①②③
给出下面三个推导过程:
①为正实数,,当且仅当时,等号成立;
②R,,,当且仅当时,等号成立;
③,∈R,,,当且仅当时,等号成立.
其中正确的推导为( )
课堂探究
【练习】
B
解析 ③由,得,均为负数,但在推导过程中将整体提取负号后,, 均变为正数,符合基本不等式的条件,故③正确.
A. B.
C. D.
(1)比较大小
【例题1】若,则下列不等式一定成立的是( )
课堂探究
C
解析 (方法1 直接法)
∵,∴,∴.
∵,∴,∴ .
故.故选C.
A. B.
C. D.
课堂探究
解析 (方法2 特值法)
∵,
∴取则排除A,B,D.
故选C.
(1)比较大小
【例题1】若,则下列不等式一定成立的是( )
C
课堂探究
【小结】
运用基本不等式判断所给的不等关系是否正确时,一般有两种处理方法:
(1)若基本不等式成立,进行合理的变形推导.
(2)选取合适的特殊值,举反例排除.注意,特殊值法只能作排除使用,不能作不等式成立的依据.
【跟踪训练1】
设则四个数中最小的是 .
课堂探究
解析 (方法1)因为所以.
又因为所以<1,得
综上,最小.
(方法2)取则所以最小.
课堂探究
证明 因为
所以
所以
当且仅当即时等号成立.
(2)证明不等式
【例题2】已知,求证:.
课堂探究
【小结】
证明不等式的注意点:
(1)基本不等式使用的条件:等号成立的条件是
(2)注意等号成立的条件要一致,若不一致则等号取不到.
(3)注意不等式性质使用的正确性.
【跟踪训练2】
已知是全不相等的正数,求证:.
课堂探究
证明 ∵都是正数,
∴等号成立的条件为.
等号成立的条件为.
两式相乘,得
等号成立的条件为且.
又全不相等,
故.
课堂探究
提示 本题可拓展为当时,,当且仅当,即时,等号成立.
(3)求最值
【例题3】已知,求的最小值.
解析 因为,所以,
当且仅当,即时,等号成立,
的最小值是.
课堂探究
【小结】
已知都是正数,
(1)如果积等于定值,那么当时,和有最小值;
(2)如果和等于定值,那么当时,积有最大值.
可简记为“积定和最小,和定积最大”.
【跟踪训练3】
(1)已知求的最小值;
课堂探究
解 ∵,∴,
当且仅当,即时,等号成立.
故的最小值为
【跟踪训练3】
(2)已知,且求的最大值;
课堂探究
解 ∵,且,
∴由基本不等式,得,
当且仅当时,取到最大值.
∴的最大值为.
【跟踪训练3】
(3)已知求的最大值;
课堂探究
解 ∵ ,
∴,
∴,
当且仅当,即时,等号成立.
故当时,
【跟踪训练3】
(4)已知,求的最大值.
课堂探究
解 ∵
∴
∴
当且仅当
即时,等号成立.
故当时,.
【例题4】(1)用篱笆围成一个面积为100m的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短.最短的篱笆是多少
课堂探究
A
B
D
C
课堂探究
解 设矩形菜园的长为m,宽为m,则,篱笆的长为m.
,
,
∴,
结论1:两个正变量积为定值,则和有最小值,当且仅当两变量值相等时取最值.简记“积定和最小”.
【例题4】(2)用一段长为36m的篱笆围成一个矩形菜园,问这个矩形菜园的长和宽各为多少时,菜园的面积最大,最大面积是多少
课堂探究
A
B
D
C
课堂探究
解 设矩形菜园的长为 m,宽为 m,则.
矩形菜园的面积为
,
.
结论2:两个正变量和为定值,则积有最大值,当且仅当两变量值相等时取最值.简记“和定积最大”.
【跟踪训练4】
某游泳馆拟建一个平面图形为矩形且面积为200 m2的泳池,池的深度为1 m,池的四周墙壁建造单价为每米400元,中间一条横向的隔壁建造单价为每米100元,池底建造单价为每平方米60元(池壁厚忽略不计),则泳池的长设计为多少米时,可使总造价最低
课堂探究
解 设泳池的长为 m则宽为 m总造价为元则总造价
整理得到
且仅当时等号成立即泳池的长设计为m时可使总造价最低.
1. 不等式中等号成立的条件是( )
A. B.
C. D.
评价反馈
解析 由基本不等式知等号成立的条件为,即舍去).故选C.
C
2. (1)若,则的最大值为 .
(2)若且则的最大值为 .
评价反馈
解析 (1)(方法1)∵,∴.
∴· 2=,
当且仅当即时,等号成立.
∴当时,取得最大值.
2. (1)若,则的最大值为 .
(2)若且则的最大值为 .
评价反馈
(方法2)∵,∴.
∴ ) ≤3· (,
当且仅当即时,等号成立.
∴当时,取得最大值.
(2)∵∴解得当且仅当时,等号成立.
3. 已知求证:.
评价反馈
证明 ∵
∴当且仅当时,等号成立,,当且仅当时,等号成立,,当且仅当时,等号成立.
∴,即,当且仅当时,等号成立.
4. 某养殖公司欲将一批冷鲜肉用冷藏汽车从甲地运往相距120 km的乙地,运费为每小时60元,装卸费为1000元,冷鲜肉在运输途中的损耗费(单位:元)是汽车速度值(单位:km/h)的2倍.(说明:运输的总费用=运费+装卸费+损耗费)
(1)写出运输的总费用(单位:元)与汽车速度(单位:km/h)的函数关系式,并求汽车速度为50 km/h时运输的总费用.
(2)求汽车行驶速度为何值时,运输的总费用最小,最小值为多少
评价反馈
评价反馈
解 (1),
当汽车速度为50 km/h时,运输总费用为(元).
(2)由(1)得,当,即时,等号成立.
故汽车行驶速度为60 km/h时,运输的总费用最小,最小值为1240元.
课堂小结
1.基础知识归纳
(1)基本不等式及其证明、几何解释;
(2)基本不等式的应用,尤其是利用基本不等式求最值.
2.思想方法总结:转化与化归思想
3.误区警示:忽视基本不等式使用前提以及等号成立的条件;利用基本不等式求最值时忽略“一正,二定,三相等”.
布置作业
认真整理本节知识脉络,完成学案.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
