第二章 2.3二次函数与一元二次方程、不等式--人教A版高中数学必修第一册教学课件(共39张PPT)
文档属性
| 名称 | 第二章 2.3二次函数与一元二次方程、不等式--人教A版高中数学必修第一册教学课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:29:21 | ||
图片预览










文档简介
(共39张PPT)
2.3 二次函数与一元二次
方程、不等式
第二章 一元二次函数、方程和不等式
数学
学习目标
①经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.
②借助二次函数的图象,了解一元二次不等式与相应函数、方程的联系,体会数学的整体性.
③能借助二次函数求解不含参数或含参数的一元二次不等式、分式不等式,并能利用一元二次不等式解决一些实际应用问题.
④借助三个“二次”的关系,解决不等式恒成立问题以及利用不等式的解集求参数.
重点:
二次函数与一元二次方程、不等式的联系,借助二次函数求解一元二次不等式,不等式的恒成立问题以及求参数问题.
难点:
二次函数与一元二次方程、不等式的联系,借助二次函数求解一元二次不等式,不等式的恒成立问题以及求参数问题.
课堂导入
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2 ,则这个矩形的边长为多少米
解 设这个矩形的一条边长为x m,则另一条边长为(12 x)m.
由题意,得(12 x)x>20,其中x∈{x|0整理,得x2 12x+20<0,x∈{x|0课堂探究
在上题中我们得到这样一个不等式:x2 12x+20<0,x∈{x|0探究一 一元二次不等式的概念
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.它的一般形式是
ax2+bx+c>0或ax2+bx+c<0,
其中a,b,c都是常数且a0.
课堂探究
探究一 一元二次不等式的概念
1.“一元”指的是只有一个未知数,不代表只有一个字母,如a,b,c等均可;
2.“二次”指的是未知数的最高次必须存在并且次数为2.
课堂探究
画出二次函数y = x2 5x的图象.
探究二 “三个二次”的关系
0
5
x
y
y=x2 5x
当 时,.
方程x2 5x=0的根为:x=0,5 .
当 时,.
当 时,.
由图象可知:
不等式x2 5x>0的解集为 ;
不等式x2 5x0的解集为 .
x=0或5
0x<0或x>5
{x|x<0或x>5}
{x|0x5}
课堂探究
(一元二次不等式的解集与一元二次方程、二次函数的图象的关系)
探究二 “三个二次”的关系
ax2+bx+c=0 (a>0)的根
y=ax2+bx+c
(a>0)的图象
没有实根
两个不等实根()
()
两个相等实根
ax2+bx+c>0 (a>0)的解集
ax2+bx+c<0 (a>0)的解集
x
课堂探究
(一元二次不等式的解集与一元二次方程、二次函数的图象的关系)
探究二 “三个二次”的关系
x1
x2
x
x
x
x1=x2
x
x
x1
x2
课堂探究
三个“二次”关系的实质用数形结合的思想来解读:
的解的图象与x轴的交点的横坐标;
的解集的图象上的点(x,y)处于x轴
上方时,对应的的取值范围的集合;
的解集的图象上的点处于轴
下方时,对应的的取值范围的集合.
课堂探究
解下列不等式:
(1)2x2+x 3>0;
【例题1】
解 (1)由2x2+x 3>0,可得(2x+3)(x 1)>0,故不等式2x2+x 3>0的解集为{x|x< ,或x>1}.
探究三 解一元二次不等式
课堂探究
解下列不等式:
(2)≥3.
【例题1】
解 (方法1) ≥3 3≥0 ≤0
解得2(方法2)在≥3的两边同乘(x 2)2,得(x+1)(x 2)≥3(x 2)2且x 2≠0,
即2x2 11x+14≤0且x≠2,解得2探究三 解一元二次不等式
课堂探究
解一元二次不等式的一般步骤:
(1)化标准.通过对不等式进行变形,使不等式右侧为0,使二次项系数为正.
(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画图象.根据一元二次方程根的情况画出对应的二次函数的图象.
(5)写解集.根据图象写出不等式的解集.
探究三 解一元二次不等式
课堂探究
解关于x的不等式ax2 (2a+1)x+2≤0,其中a∈R.
【例题2】
解 由题意,得ax2 (2a+1)x+2≤0 (x 2)(ax 1)≤0.
①当a=0时, x+2≤0,解得x≥2,
故原不等式的解集为{x|x≥2}.
②当a<0时,原不等式可化为(x 2)(x )≥0,解得x≥2,或x≤,
故原不等式的解集为{x|x≤,或x≥2}.
探究四 解含参数的一元二次不等式
课堂探究
【例题2】
③当a>0时,原不等式可化为(x 2)(x )≤0,
当=2,即a=时,解得x=2,故原不等式的解集为{2};
当>2,即0当<2,即a>时,解得≤x≤2,故原不等式的解集为{x|≤x≤2}.
探究四 解含参数的一元二次不等式
课堂探究
【例题2】
探究四 解含参数的一元二次不等式
综上,当a<0时,原不等式的解集为{x|x≤,或x≥2};
当a=0时,原不等式的解集为{x|x≥2};
当0当a=时,原不等式的解集为{2};
当a>时,原不等式的解集为{x|≤x≤2}.
课堂探究
探究四 解含参数的一元二次不等式
讨论二次项系数
判断方程根的个数
写出解集
二次项若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为二次项系数为正数的形式
判断方程的根的个数,讨论判别式与0的关系
确定无根时可直接写出解集确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式
一般步骤
课堂探究
【跟踪训练1】
解关于x的不等式ax2 (a+1)x+1<0.
解 原不等式可化为(ax 1)(x 1)<0.
∵当a=0时, x+1<0,∴ x>1;
当a<0时,原不等式可化为(x )(x 1)>0,
∵ <1, ∴ x<或x>1;
当a>0时,原不等式可化为(x )(x 1)<0,
若<1,即a>1,则课堂探究
【跟踪训练1】
若=1,即a=1,则x∈ ;
若>1,即0综上所述,当a<0时,原不等式的解集为{x|x<,或x>1};当a=0时,原不等式的解集为{x|x>1};当01时,原不等式的解集为{x|课堂探究
已知函数y=ax2+bx a+2,若关于x的不等式ax2+bx a+2>0的解集是{x| 1【例题3】
解 因为不等式ax2+bx a+2>0的解集是{x| 1由一元二次方程根与系数的关系, 解得
探究四 利用不等式的解集求参数
课堂探究
已知不等式的解集求参数
转化法
通过一元二次不等式的解集转化为一元二次方程根和二次函数图象开口方向的问题
方程的根与系数的关系以及二次项系数的正负
求得参数
探究四 利用不等式的解集求参数
课堂探究
已知不等式ax2+5x 2>0的解集是{x|(1)求不等式ax2 5x+a2 1>0的解集;
(2)已知二次不等式ax2+bx+c<0的解集为{x|x<,或x>},求关于x的不等式cx2 bx+a>0的解集.
【跟踪训练2】
探究四 利用不等式的解集求参数
课堂探究
解 (1)由题意知,关于x的二次方程ax2+5x 2=0的两根为2和,且a<0.
由根与系数的关系,得解得a= 2,
所以不等式ax2 5x+a2 1>0即为 2x2 5x+3>0,
即2x2+5x 3<0,解得 3所以不等式ax2 5x+a2 1>0的解集为{x| 3【跟踪训练2】
探究四 利用不等式的解集求参数
课堂探究
已知不等式ax2+5x 2>0的解集是{x|(2)已知二次不等式ax2+bx+c<0的解集为{x|x<,或x>},求关于x的不等式cx2 bx+a>0的解集.
【跟踪训练2】
探究四 利用不等式的解集求参数
解 (2)由(1)知a= 2,由题意知,关于x的二次方程 2x2+bx+c=0的两根为.
由根与系数的关系,得解得
所以不等式cx2 bx+a>0,即 x2 x 2>0,即x2+5x+6<0,解得 3所以关于x的不等式cx2 bx+a>0的解集为{x| 3课堂探究
已知关于x的一元二次不等式kx2 3x+k≤0的解集为R,求实数k的取值范围.
【例题4】
解 由题意,关于x的不等式kx2 3x+k≤0的解集为R.
当k=0时, 3x≤0,不恒成立;
当k≠0时,解得k≤ ,
综上,实数k的取值范围是{k|k≤ }.
探究五 大小与不等式解集的关系
课堂探究
将原不等式化成的形式
计算的值
方程有两个不等实根( )
原不等式的解集为
{|}
方程有两个相等实根( )
原不等式的解集为
{|}
方程
没有实根
原不等式的解集为
探究五 大小与不等式解集的关系
课堂探究
已知关于x的不等式2kx2+kx <0恒成立,求实数k的取值范围.
【跟踪训练3】
解 当k=0时,原不等式为 <0,恒成立;
当k≠0时,要使原不等式恒成立,则解得 3综上,实数k的取值范围为{k| 3探究五 大小与不等式解集的关系
课堂探究
为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数y+500.
(1)设他每月获得的利润为w(单位:元),写出他每月获得的利润w与销售单价x的函数关系.
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
解 (1)依题意可知每件节能灯的销售利润为(x 10)元,每月的销售量为( 10x+500)件,所以每月获得的利润w与销售单价x的函数关系为w=(x 10)( 10x+500).
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数y+500.
(2)相关部门规定,这种节能灯的销售单价不得高于25元.如果他想要每月获得的利润不少于3000元,那么政府每个月为他承担的总差价的取值范围是多少
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
解 (2)由每月获得的利润不少于元,得(x 10)·( 10x+500)≥3 000,
化简得x2 60x+800≤0,解得20≤x≤40.
又因为这种节能灯的销售单价不得高于25元,所以20≤x≤25.
设政府每个月为他承担的总差价为p元,则p=(12 10)( 10x+500)= 20x+1000.
由20≤x≤25,得500≤ 20x+1000≤600,
故政府每个月为他承担的总差价的取值范围为{p|500≤p≤600}.
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
一元二次不等式应用题的解法:
(1)设未知数,并用未知数表示问题中的有关量.
(2)由题中给出的不等关系,列出关于未知数的不等式或不等式组.
(3)解所列出的不等式或不等式组.
(4)结合问题的实际意义写出答案.
探究六 用一元二次不等式解决实际应用问题
评价反馈
1. 若关于x的不等式ax2+bx+c≥0的解集为{x|x≤ 3,或x≥4},则下列说法正确的是( )
A.a<0
B.不等式bx+c>0的解集为{x|x> 12}
C.不等式cx2 bx+a<0的解集为{x|x< ,或x>}
D.a+b+c>0
C
解析 ∵关于x的不等式ax2+bx+c≥0的解集为{x|x≤ 3,或x≥4},
∴二次函数y=ax2+bx+c的图象开口向上,即a>0,选项A错误;
由题意可得 3,4是方程ax2+bx+c=0的两个实数根,则解得
故不等式bx+c>0等价于 ax 12a>0.
又a>0,∴x< 12,即不等式bx+c>0的解集为{x|x< 12},选项B错误;
由,得不等式cx2 bx+a<0可化为 12ax2+ax+a<0,即12x2 x 1>0,解得x< ,或x>,∴不等式cx2 bx+a<0的解集为,选项C正确;
由(a>0),得a+b+c=a a 12a= 12a<0,选项D错误.故选C.
评价反馈
评价反馈
2. 若不等式ax2+(a 1)x+a>0对任意x∈R恒成立,则实数a的取值范围是( )
A.{a|a< 1,或a>} B.{a|a>1}
C.{a|a>} D.{a| 1C
解析 ∵当时,>0,∴<0,不符合题意,舍去;
当≠0时,由题意得>0且,
∴.
综上,实数的取值范围是{| }.
评价反馈
3. 解关于x的不等式x2 (a+a2)x+a3>0(a∈R).
解 原不等式可化为(x a)(x a2)>0.
当a<0时,aa2};
当a=0时,a2=a,原不等式的解集为{x|x≠0};
当0a};
当a=1时,a2=a,原不等式的解集为{x|x≠1};
当a>1时,aa2}.
综上所述,当a<0或a>1时,原不等式的解集为{x|xa2};
当0a};
当a=1时,原不等式的解集为{x|x≠1};
当a=0时,原不等式的解集为{x|x≠0}.
课堂小结
1. 基础知识归纳
(1)一元二次不等式的定义及现实意义.
(2)一元二次不等式与相应函数、方程的联系.
(3)借助二次函数求解一元二次不等式,并利用一元二次不等式解决一些实际应用问题.
2. 思想方法总结:数形结合思想、类比思想、分类讨论思想、数学建模思想、函数方法.
3. 误区警示
(1)解一元二次不等式时,常使不等式右侧为0,二次项系数为正数.
(2)含参数的不等式在求解时,对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集,不能合并.
布置作业
认真整理本节所讲,梳理知识脉络,完成学案的核心素养专练.
谢谢大家
2.3 二次函数与一元二次
方程、不等式
第二章 一元二次函数、方程和不等式
数学
学习目标
①经历从实际情境中抽象出一元二次不等式的过程,了解一元二次不等式的现实意义.
②借助二次函数的图象,了解一元二次不等式与相应函数、方程的联系,体会数学的整体性.
③能借助二次函数求解不含参数或含参数的一元二次不等式、分式不等式,并能利用一元二次不等式解决一些实际应用问题.
④借助三个“二次”的关系,解决不等式恒成立问题以及利用不等式的解集求参数.
重点:
二次函数与一元二次方程、不等式的联系,借助二次函数求解一元二次不等式,不等式的恒成立问题以及求参数问题.
难点:
二次函数与一元二次方程、不等式的联系,借助二次函数求解一元二次不等式,不等式的恒成立问题以及求参数问题.
课堂导入
园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2 ,则这个矩形的边长为多少米
解 设这个矩形的一条边长为x m,则另一条边长为(12 x)m.
由题意,得(12 x)x>20,其中x∈{x|0
在上题中我们得到这样一个不等式:x2 12x+20<0,x∈{x|0
一般地,我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.它的一般形式是
ax2+bx+c>0或ax2+bx+c<0,
其中a,b,c都是常数且a0.
课堂探究
探究一 一元二次不等式的概念
1.“一元”指的是只有一个未知数,不代表只有一个字母,如a,b,c等均可;
2.“二次”指的是未知数的最高次必须存在并且次数为2.
课堂探究
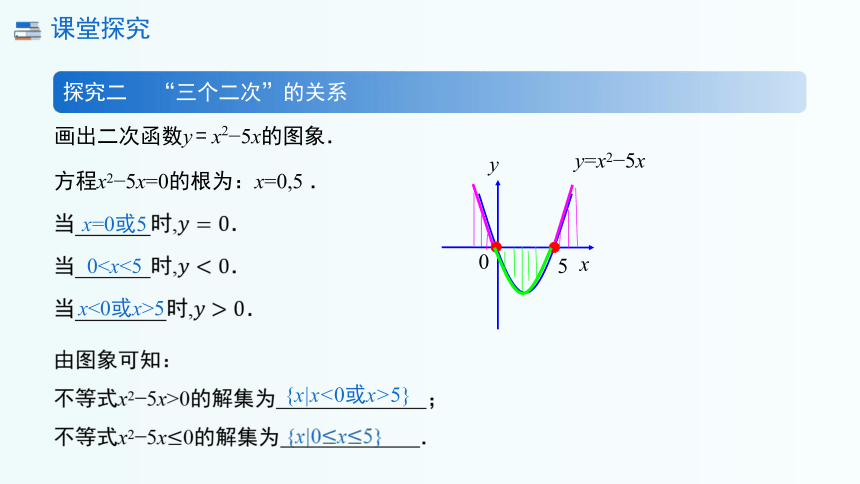
画出二次函数y = x2 5x的图象.
探究二 “三个二次”的关系
0
5
x
y
y=x2 5x
当 时,.
方程x2 5x=0的根为:x=0,5 .
当 时,.
当 时,.
由图象可知:
不等式x2 5x>0的解集为 ;
不等式x2 5x0的解集为 .
x=0或5
0
{x|x<0或x>5}
{x|0x5}
课堂探究
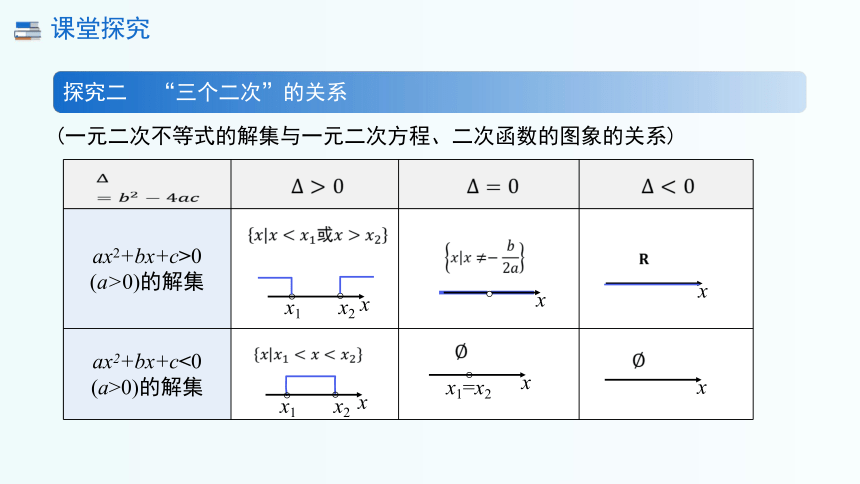
(一元二次不等式的解集与一元二次方程、二次函数的图象的关系)
探究二 “三个二次”的关系
ax2+bx+c=0 (a>0)的根
y=ax2+bx+c
(a>0)的图象
没有实根
两个不等实根()
()
两个相等实根
ax2+bx+c>0 (a>0)的解集
ax2+bx+c<0 (a>0)的解集
x
课堂探究
(一元二次不等式的解集与一元二次方程、二次函数的图象的关系)
探究二 “三个二次”的关系
x1
x2
x
x
x
x1=x2
x
x
x1
x2
课堂探究
三个“二次”关系的实质用数形结合的思想来解读:
的解的图象与x轴的交点的横坐标;
的解集的图象上的点(x,y)处于x轴
上方时,对应的的取值范围的集合;
的解集的图象上的点处于轴
下方时,对应的的取值范围的集合.
课堂探究
解下列不等式:
(1)2x2+x 3>0;
【例题1】
解 (1)由2x2+x 3>0,可得(2x+3)(x 1)>0,故不等式2x2+x 3>0的解集为{x|x< ,或x>1}.
探究三 解一元二次不等式
课堂探究
解下列不等式:
(2)≥3.
【例题1】
解 (方法1) ≥3 3≥0 ≤0
解得2
即2x2 11x+14≤0且x≠2,解得2
课堂探究
解一元二次不等式的一般步骤:
(1)化标准.通过对不等式进行变形,使不等式右侧为0,使二次项系数为正.
(2)判别式.对不等式左侧因式分解,若不易分解,则计算对应方程的判别式.
(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.
(4)画图象.根据一元二次方程根的情况画出对应的二次函数的图象.
(5)写解集.根据图象写出不等式的解集.
探究三 解一元二次不等式
课堂探究
解关于x的不等式ax2 (2a+1)x+2≤0,其中a∈R.
【例题2】
解 由题意,得ax2 (2a+1)x+2≤0 (x 2)(ax 1)≤0.
①当a=0时, x+2≤0,解得x≥2,
故原不等式的解集为{x|x≥2}.
②当a<0时,原不等式可化为(x 2)(x )≥0,解得x≥2,或x≤,
故原不等式的解集为{x|x≤,或x≥2}.
探究四 解含参数的一元二次不等式
课堂探究
【例题2】
③当a>0时,原不等式可化为(x 2)(x )≤0,
当=2,即a=时,解得x=2,故原不等式的解集为{2};
当>2,即0
探究四 解含参数的一元二次不等式
课堂探究
【例题2】
探究四 解含参数的一元二次不等式
综上,当a<0时,原不等式的解集为{x|x≤,或x≥2};
当a=0时,原不等式的解集为{x|x≥2};
当0
当a>时,原不等式的解集为{x|≤x≤2}.
课堂探究
探究四 解含参数的一元二次不等式
讨论二次项系数
判断方程根的个数
写出解集
二次项若含有参数应讨论是等于0,小于0,还是大于0,然后将不等式转化为二次项系数为正数的形式
判断方程的根的个数,讨论判别式与0的关系
确定无根时可直接写出解集确定方程有两个根时,要讨论两根的大小关系,从而确定解集形式
一般步骤
课堂探究
【跟踪训练1】
解关于x的不等式ax2 (a+1)x+1<0.
解 原不等式可化为(ax 1)(x 1)<0.
∵当a=0时, x+1<0,∴ x>1;
当a<0时,原不等式可化为(x )(x 1)>0,
∵ <1, ∴ x<或x>1;
当a>0时,原不等式可化为(x )(x 1)<0,
若<1,即a>1,则
【跟踪训练1】
若=1,即a=1,则x∈ ;
若>1,即0
已知函数y=ax2+bx a+2,若关于x的不等式ax2+bx a+2>0的解集是{x| 1
解 因为不等式ax2+bx a+2>0的解集是{x| 1
探究四 利用不等式的解集求参数
课堂探究
已知不等式的解集求参数
转化法
通过一元二次不等式的解集转化为一元二次方程根和二次函数图象开口方向的问题
方程的根与系数的关系以及二次项系数的正负
求得参数
探究四 利用不等式的解集求参数
课堂探究
已知不等式ax2+5x 2>0的解集是{x|
(2)已知二次不等式ax2+bx+c<0的解集为{x|x<,或x>},求关于x的不等式cx2 bx+a>0的解集.
【跟踪训练2】
探究四 利用不等式的解集求参数
课堂探究
解 (1)由题意知,关于x的二次方程ax2+5x 2=0的两根为2和,且a<0.
由根与系数的关系,得解得a= 2,
所以不等式ax2 5x+a2 1>0即为 2x2 5x+3>0,
即2x2+5x 3<0,解得 3
探究四 利用不等式的解集求参数
课堂探究
已知不等式ax2+5x 2>0的解集是{x|
【跟踪训练2】
探究四 利用不等式的解集求参数
解 (2)由(1)知a= 2,由题意知,关于x的二次方程 2x2+bx+c=0的两根为.
由根与系数的关系,得解得
所以不等式cx2 bx+a>0,即 x2 x 2>0,即x2+5x+6<0,解得 3
已知关于x的一元二次不等式kx2 3x+k≤0的解集为R,求实数k的取值范围.
【例题4】
解 由题意,关于x的不等式kx2 3x+k≤0的解集为R.
当k=0时, 3x≤0,不恒成立;
当k≠0时,解得k≤ ,
综上,实数k的取值范围是{k|k≤ }.
探究五 大小与不等式解集的关系
课堂探究
将原不等式化成的形式
计算的值
方程有两个不等实根( )
原不等式的解集为
{|}
方程有两个相等实根( )
原不等式的解集为
{|}
方程
没有实根
原不等式的解集为
探究五 大小与不等式解集的关系
课堂探究
已知关于x的不等式2kx2+kx <0恒成立,求实数k的取值范围.
【跟踪训练3】
解 当k=0时,原不等式为 <0,恒成立;
当k≠0时,要使原不等式恒成立,则解得 3
课堂探究
为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数y+500.
(1)设他每月获得的利润为w(单位:元),写出他每月获得的利润w与销售单价x的函数关系.
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
解 (1)依题意可知每件节能灯的销售利润为(x 10)元,每月的销售量为( 10x+500)件,所以每月获得的利润w与销售单价x的函数关系为w=(x 10)( 10x+500).
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
为鼓励大学毕业生自主创业,某市出台了相关政策:由政府协调,企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.某大学毕业生按照相关政策投资销售一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月的销售量y(单位:件)与销售单价x(单位:元)之间的关系近似满足一次函数y+500.
(2)相关部门规定,这种节能灯的销售单价不得高于25元.如果他想要每月获得的利润不少于3000元,那么政府每个月为他承担的总差价的取值范围是多少
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
解 (2)由每月获得的利润不少于元,得(x 10)·( 10x+500)≥3 000,
化简得x2 60x+800≤0,解得20≤x≤40.
又因为这种节能灯的销售单价不得高于25元,所以20≤x≤25.
设政府每个月为他承担的总差价为p元,则p=(12 10)( 10x+500)= 20x+1000.
由20≤x≤25,得500≤ 20x+1000≤600,
故政府每个月为他承担的总差价的取值范围为{p|500≤p≤600}.
【例题5】
探究六 用一元二次不等式解决实际应用问题
课堂探究
一元二次不等式应用题的解法:
(1)设未知数,并用未知数表示问题中的有关量.
(2)由题中给出的不等关系,列出关于未知数的不等式或不等式组.
(3)解所列出的不等式或不等式组.
(4)结合问题的实际意义写出答案.
探究六 用一元二次不等式解决实际应用问题
评价反馈
1. 若关于x的不等式ax2+bx+c≥0的解集为{x|x≤ 3,或x≥4},则下列说法正确的是( )
A.a<0
B.不等式bx+c>0的解集为{x|x> 12}
C.不等式cx2 bx+a<0的解集为{x|x< ,或x>}
D.a+b+c>0
C
解析 ∵关于x的不等式ax2+bx+c≥0的解集为{x|x≤ 3,或x≥4},
∴二次函数y=ax2+bx+c的图象开口向上,即a>0,选项A错误;
由题意可得 3,4是方程ax2+bx+c=0的两个实数根,则解得
故不等式bx+c>0等价于 ax 12a>0.
又a>0,∴x< 12,即不等式bx+c>0的解集为{x|x< 12},选项B错误;
由,得不等式cx2 bx+a<0可化为 12ax2+ax+a<0,即12x2 x 1>0,解得x< ,或x>,∴不等式cx2 bx+a<0的解集为,选项C正确;
由(a>0),得a+b+c=a a 12a= 12a<0,选项D错误.故选C.
评价反馈
评价反馈
2. 若不等式ax2+(a 1)x+a>0对任意x∈R恒成立,则实数a的取值范围是( )
A.{a|a< 1,或a>} B.{a|a>1}
C.{a|a>} D.{a| 1
解析 ∵当时,>0,∴<0,不符合题意,舍去;
当≠0时,由题意得>0且,
∴.
综上,实数的取值范围是{| }.
评价反馈
3. 解关于x的不等式x2 (a+a2)x+a3>0(a∈R).
解 原不等式可化为(x a)(x a2)>0.
当a<0时,a
当a=0时,a2=a,原不等式的解集为{x|x≠0};
当0
当a=1时,a2=a,原不等式的解集为{x|x≠1};
当a>1时,a
综上所述,当a<0或a>1时,原不等式的解集为{x|x
当0
当a=1时,原不等式的解集为{x|x≠1};
当a=0时,原不等式的解集为{x|x≠0}.
课堂小结
1. 基础知识归纳
(1)一元二次不等式的定义及现实意义.
(2)一元二次不等式与相应函数、方程的联系.
(3)借助二次函数求解一元二次不等式,并利用一元二次不等式解决一些实际应用问题.
2. 思想方法总结:数形结合思想、类比思想、分类讨论思想、数学建模思想、函数方法.
3. 误区警示
(1)解一元二次不等式时,常使不等式右侧为0,二次项系数为正数.
(2)含参数的不等式在求解时,对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集,不能合并.
布置作业
认真整理本节所讲,梳理知识脉络,完成学案的核心素养专练.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
