第四章 4.3.2对数的运算--人教A版高中数学必修第一册教学课件(共36张PPT)
文档属性
| 名称 | 第四章 4.3.2对数的运算--人教A版高中数学必修第一册教学课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:34:21 | ||
图片预览











文档简介
(共36张PPT)
4.3.2 对数的运算
第四章 指数函数与对数函数
数学
学习目标
①通过指数幂的运算性质推导出对数的运算性质.
②掌握对数换底公式,能够用换底公式简化问题.
学习重难点
重点:
对数的运算性质,换底公式,对数恒等式及其应用.
难点:
正确使用对数的运算性质和换底公式.
课堂导入
1. 对数
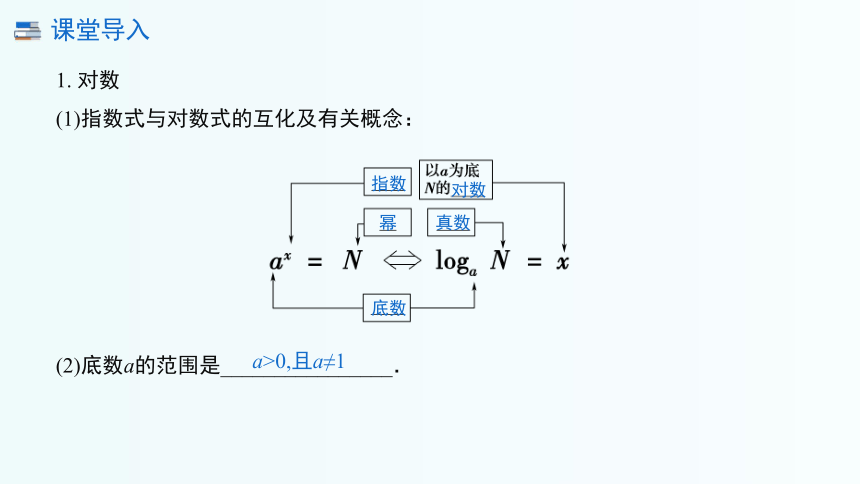
(1)指数式与对数式的互化及有关概念:
指数
对数
幂
真数
底数
(2)底数a的范围是________________.
a>0,且a≠1
课堂导入
2. 指数幂的运算性质:
(1) =
(2)
(3)
3. 对数的性质:
(1)零和负数没有对数,即真数;
(2)的对数为即
(3)底数的对数等于1,即.
课堂导入
问题
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢
课堂探究
探究一 对数的运算性质
将指数式,化为对数式,log,log.
结合指数的运算性质能否将化为对数式
=log
它们之间有何关系
从而得出
.
课堂探究
探究一 对数的运算性质
结合前面的推导,由指数式又能得到什么样的结论
由
得
.
课堂探究
探究一 对数的运算性质
结合前面的推导,由指数式又能得到什么样的结论
由
得
课堂探究
对数的运算性质
如果,且,,,那么
(1)loglog+log;
(2)loglogloga;
(3)loglog().
方法感知
(1)log84+log82=
(2)log510 log52=
(3)lg=
(4)若ln a=0.2,则ln=
lg 10=.
log88=1.
log55=1.
ln e ln a=1 0.2=0.8.
课堂探究
思考1
在积的对数运算性质中,三项的乘积式log是否适用 你能得到一个怎样的结论
适用,loglogloglog,积的对数运算性质可以推广到真数是个正数的乘积.
课堂探究
【例题1】
计算下列各式的值:
(1)(lg 5)2+2lg 2(lg 2)2;(2);(3)log5352log5+log57 log51.8.
解 (1)原式=(lg 5)2+(2lg 2)lg 2=(lg 5)2+(1+lg 5)lg 2=(lg 5)2+lg 2·lg 5+lg 2=(lg 5+lg 2)·lg 5+lg 2=lg 5+lg 2=1.
(2)原式===.
(3)原式=log5(5×7)2(log57log53)+log57log5=log55+log572log57+2log53+
log572log53+log55=2log55=2.
课堂探究
反思感悟
对数式化简与求值的基本原则和方法
(1)基本原则:对数式的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)两种常用的方法
①“收”,将同底的两对数的和(差)收成积(商)的对数;
②“拆”,将积(商)的对数拆成同底的两对数的和(差).
课堂探究
【跟踪训练1】
计算下列各式的值:
(1)log5;
(2)log2(32×42).
解 (1)log5log5625=log554=.
(2)log2(32×42)=log232+log242=5+4=9.
课堂探究
【例题2】
用logax,logay,logaz表示下列各式:
(1)loga(xy2);(2)loga(x);(3)loga.
解 (1)loga(xy2)=logax+logay2=logax+2logay.
(2)loga(x)=logax+loga=logax+logay.
(3)logaloga[logax-loga(yz2)]=(logax-logay-2logaz).
对对数式进行计算、化简时,一要注意准确应用对数的性质和运算性质,二要注意取值范围对符号的限制.
课堂探究
【跟踪训练2】
用logax,logay,logaz表示下列各式:
(1)loga(x3y5);(2)loga.
解 (1)loga(x3y5)=logax3+logay5=3logax+5logay.
(2)loga=logaloga(yz)=loga-(logay+logaz)=logax-logay-logaz.
课堂探究
探究二 换底公式
思考2:
假设=x,则log25=xlog23,即log25=log23x,可得3x=5,由指数和对数的关系可得x=log35,因此=log35.如果将底数换成c(c>0,且c≠1)等式还成立吗
提示 成立,推导如下:
假设=x,则logc5=xlogc3,即logc5=logc3x,
可得3x=5,由指数和对数的关系可得x=log35,因此=log35.
课堂探究
探究二 换底公式
思考3:
这个等式能否推广到任意底数的对数式 会得到什么样的式子 你能写出它的推导过程吗
提示 将公式进行推广,可得logab=(a>0,且a≠1;c>0,且c≠1;b>0)
推导如下:
假设=x,则logcb=xlogca,即logcb=logcax,可得ax=b,
由指数和对数的关系可得x=logab,故=logab.
课堂探究
探究二 换底公式
设 logab=x,则ax=b,于是有 logcax=logcb.
根据对数运算性质(3)有:xlogca=logcb,
即:,且且
这个式子叫做对数的换底公式,简称为换底公式.
★ 换底公式的意义:把不同底数问题转化为同底数问题,也可以反过来用.
★ 换底公式的条件:公式中每一个对数式都有意义.
★ 换底公式换的底:依据具体问题需要而变.
课堂探究
归纳总结
换底公式常见的推论.
(1)lolog;
(2)lo log,特别地,log;
(3)loglog 1;
(4)log·loglog log
课堂探究
【例题3】
计算:(1)(log43+log83)(log32+log92) lo;
(2)(log43 log83)(log32 log92).
解 (1)(log43+log83)(log32+log92) lo
=()(log32+) =(log23+log23)(log32+log32)+log232
=log23×log32+.
课堂探究
【例题3】
计算:(1)(log43+log83)(log32+log92) lo;
(2)(log43log83)(log32log92).
解 (2)(log43log83)(log32log92)
=()()=()()==.
课堂探究
【跟踪训练3】
求值.
解
=lo·lo9=lo·3lo
= ·log32·3log23= .
课堂探究
1. 换底公式的本质是化异底为同底,主要用途是将一般对数化为常用对数或自然对数,解决一般对数的求值问题.
2. 利用换底公式计算、化简、求值的一般思路:
3.应用换底公式时注意:
(1)换底公式的正用、逆用以及变形应用;
(2)题目中有指数式和对数式时,要注意指数式与对数式统一形式.
课堂探究
【例题4】
已知log189=a,18b=5,求log3645.(用a,b表示)
解 (方法1)∵log189=a,18b=5,∴log185=b,
于是log3645=.
(方法2)∵log189=a,18b=5,∴lg 9=alg 18,lg 5=blg 18,
∴log3645=.
探究三 对数式与指数式的综合运用
课堂探究
【延伸拓展】
已知log23=a,log37=b,用a,b表示log4256.
解 ∵log23=a,则=log32,又∵log37=b,
∴log4256=.
课堂探究
利用对数式与指数式互化求值的方法:
在对数式、指数式的互化运算中,要注意灵活运用定义、性质和运算法则,尤其要注意条件和结论之间的关系,进行正确的相互转化.
课堂探究
【跟踪训练4】
(1)设3a=4b=36,求的值;
(2)设2x=5y=m,且=2,则m= .
解 (1)(方法1)由3a=4b=36,得a=log336,b=log436,由换底公式得=log363,=log364,
故=2log363+log364=log3636=1.
(方法2)由3a=4b=36,两边取以6为底数的对数,得alog63=blog64=log636=2,
则=log63,log64=log62,故=log63+log62=log66=1.
(2)∵2x=5y=m,两边取常用对数,得x=log2m=,y=log5m=,
∴=2,∴lg m=,∴m=.
评价反馈
1. 下列等式成立的是( )
A. log2(84)=log28 log24 B. =log2
C. log223=3log22 D. log2(84)=log28+log24
C
解析 对于A:log28-log24=log2=1,故A不正确;
对于B:log2=log22=1,≠1,故B不正确;
对于C:∵logaMn=nlogaM,∴log223=3log22,故C正确;
对于D:log2(8+4)=log212,log28+log24=log2(8×4)=log225=5≠log212,故D不正确.
评价反馈
2. 2log6+3log6=( )
A. log6 B. 2 C. 0 D. 1
D
解析 2log6+3log6=log62+log63=log66=1,故选D.
评价反馈
3. 若lg 2=a,lg 3=b,则log125=( )
A. B. C. D.
C
解析 log125=.故选C.
评价反馈
4. 若logm2=a,logm3=b,则ma+2b的值为 .
18
解析 因为logm2=a,logm3=b,所以ma=2,mb=3,即ma+2b=ma×(mb)2=2×32=18.
评价反馈
5. 求值:2log32log3log38.
解 2log32log3log38
log34log3log383
log3(4××8)3
log393
=23
1.
课堂小结
本节课我们主要学习了哪些内容
1. 对数的运算性质.
2. 对数换底公式.
3. 对数运算性质的综合运用,应掌握变形技巧:
(1)各部分变形要化到最简形式,同时注意分子、分母的联系.
(2)要避免错用对数运算性质.
布置作业
完成教材第127页习题4.3第3,4,5题.
谢谢大家
4.3.2 对数的运算
第四章 指数函数与对数函数
数学
学习目标
①通过指数幂的运算性质推导出对数的运算性质.
②掌握对数换底公式,能够用换底公式简化问题.
学习重难点
重点:
对数的运算性质,换底公式,对数恒等式及其应用.
难点:
正确使用对数的运算性质和换底公式.
课堂导入
1. 对数
(1)指数式与对数式的互化及有关概念:
指数
对数
幂
真数
底数
(2)底数a的范围是________________.
a>0,且a≠1
课堂导入
2. 指数幂的运算性质:
(1) =
(2)
(3)
3. 对数的性质:
(1)零和负数没有对数,即真数;
(2)的对数为即
(3)底数的对数等于1,即.
课堂导入
问题
在引入对数之后,自然应研究对数的运算性质.你认为可以怎样研究
我们知道了对数与指数间的关系,能否利用指数幂运算性质得出相应的对数运算性质呢
课堂探究
探究一 对数的运算性质
将指数式,化为对数式,log,log.
结合指数的运算性质能否将化为对数式
=log
它们之间有何关系
从而得出
.
课堂探究
探究一 对数的运算性质
结合前面的推导,由指数式又能得到什么样的结论
由
得
.
课堂探究
探究一 对数的运算性质
结合前面的推导,由指数式又能得到什么样的结论
由
得
课堂探究
对数的运算性质
如果,且,,,那么
(1)loglog+log;
(2)loglogloga;
(3)loglog().
方法感知
(1)log84+log82=
(2)log510 log52=
(3)lg=
(4)若ln a=0.2,则ln=
lg 10=.
log88=1.
log55=1.
ln e ln a=1 0.2=0.8.
课堂探究
思考1
在积的对数运算性质中,三项的乘积式log是否适用 你能得到一个怎样的结论
适用,loglogloglog,积的对数运算性质可以推广到真数是个正数的乘积.
课堂探究
【例题1】
计算下列各式的值:
(1)(lg 5)2+2lg 2(lg 2)2;(2);(3)log5352log5+log57 log51.8.
解 (1)原式=(lg 5)2+(2lg 2)lg 2=(lg 5)2+(1+lg 5)lg 2=(lg 5)2+lg 2·lg 5+lg 2=(lg 5+lg 2)·lg 5+lg 2=lg 5+lg 2=1.
(2)原式===.
(3)原式=log5(5×7)2(log57log53)+log57log5=log55+log572log57+2log53+
log572log53+log55=2log55=2.
课堂探究
反思感悟
对数式化简与求值的基本原则和方法
(1)基本原则:对数式的化简求值一般是正用或逆用公式,对真数进行处理,选哪种策略化简,取决于问题的实际情况,一般本着便于真数化简的原则进行.
(2)两种常用的方法
①“收”,将同底的两对数的和(差)收成积(商)的对数;
②“拆”,将积(商)的对数拆成同底的两对数的和(差).
课堂探究
【跟踪训练1】
计算下列各式的值:
(1)log5;
(2)log2(32×42).
解 (1)log5log5625=log554=.
(2)log2(32×42)=log232+log242=5+4=9.
课堂探究
【例题2】
用logax,logay,logaz表示下列各式:
(1)loga(xy2);(2)loga(x);(3)loga.
解 (1)loga(xy2)=logax+logay2=logax+2logay.
(2)loga(x)=logax+loga=logax+logay.
(3)logaloga[logax-loga(yz2)]=(logax-logay-2logaz).
对对数式进行计算、化简时,一要注意准确应用对数的性质和运算性质,二要注意取值范围对符号的限制.
课堂探究
【跟踪训练2】
用logax,logay,logaz表示下列各式:
(1)loga(x3y5);(2)loga.
解 (1)loga(x3y5)=logax3+logay5=3logax+5logay.
(2)loga=logaloga(yz)=loga-(logay+logaz)=logax-logay-logaz.
课堂探究
探究二 换底公式
思考2:
假设=x,则log25=xlog23,即log25=log23x,可得3x=5,由指数和对数的关系可得x=log35,因此=log35.如果将底数换成c(c>0,且c≠1)等式还成立吗
提示 成立,推导如下:
假设=x,则logc5=xlogc3,即logc5=logc3x,
可得3x=5,由指数和对数的关系可得x=log35,因此=log35.
课堂探究
探究二 换底公式
思考3:
这个等式能否推广到任意底数的对数式 会得到什么样的式子 你能写出它的推导过程吗
提示 将公式进行推广,可得logab=(a>0,且a≠1;c>0,且c≠1;b>0)
推导如下:
假设=x,则logcb=xlogca,即logcb=logcax,可得ax=b,
由指数和对数的关系可得x=logab,故=logab.
课堂探究
探究二 换底公式
设 logab=x,则ax=b,于是有 logcax=logcb.
根据对数运算性质(3)有:xlogca=logcb,
即:,且且
这个式子叫做对数的换底公式,简称为换底公式.
★ 换底公式的意义:把不同底数问题转化为同底数问题,也可以反过来用.
★ 换底公式的条件:公式中每一个对数式都有意义.
★ 换底公式换的底:依据具体问题需要而变.
课堂探究
归纳总结
换底公式常见的推论.
(1)lolog;
(2)lo log,特别地,log;
(3)loglog 1;
(4)log·loglog log
课堂探究
【例题3】
计算:(1)(log43+log83)(log32+log92) lo;
(2)(log43 log83)(log32 log92).
解 (1)(log43+log83)(log32+log92) lo
=()(log32+) =(log23+log23)(log32+log32)+log232
=log23×log32+.
课堂探究
【例题3】
计算:(1)(log43+log83)(log32+log92) lo;
(2)(log43log83)(log32log92).
解 (2)(log43log83)(log32log92)
=()()=()()==.
课堂探究
【跟踪训练3】
求值.
解
=lo·lo9=lo·3lo
= ·log32·3log23= .
课堂探究
1. 换底公式的本质是化异底为同底,主要用途是将一般对数化为常用对数或自然对数,解决一般对数的求值问题.
2. 利用换底公式计算、化简、求值的一般思路:
3.应用换底公式时注意:
(1)换底公式的正用、逆用以及变形应用;
(2)题目中有指数式和对数式时,要注意指数式与对数式统一形式.
课堂探究
【例题4】
已知log189=a,18b=5,求log3645.(用a,b表示)
解 (方法1)∵log189=a,18b=5,∴log185=b,
于是log3645=.
(方法2)∵log189=a,18b=5,∴lg 9=alg 18,lg 5=blg 18,
∴log3645=.
探究三 对数式与指数式的综合运用
课堂探究
【延伸拓展】
已知log23=a,log37=b,用a,b表示log4256.
解 ∵log23=a,则=log32,又∵log37=b,
∴log4256=.
课堂探究
利用对数式与指数式互化求值的方法:
在对数式、指数式的互化运算中,要注意灵活运用定义、性质和运算法则,尤其要注意条件和结论之间的关系,进行正确的相互转化.
课堂探究
【跟踪训练4】
(1)设3a=4b=36,求的值;
(2)设2x=5y=m,且=2,则m= .
解 (1)(方法1)由3a=4b=36,得a=log336,b=log436,由换底公式得=log363,=log364,
故=2log363+log364=log3636=1.
(方法2)由3a=4b=36,两边取以6为底数的对数,得alog63=blog64=log636=2,
则=log63,log64=log62,故=log63+log62=log66=1.
(2)∵2x=5y=m,两边取常用对数,得x=log2m=,y=log5m=,
∴=2,∴lg m=,∴m=.
评价反馈
1. 下列等式成立的是( )
A. log2(84)=log28 log24 B. =log2
C. log223=3log22 D. log2(84)=log28+log24
C
解析 对于A:log28-log24=log2=1,故A不正确;
对于B:log2=log22=1,≠1,故B不正确;
对于C:∵logaMn=nlogaM,∴log223=3log22,故C正确;
对于D:log2(8+4)=log212,log28+log24=log2(8×4)=log225=5≠log212,故D不正确.
评价反馈
2. 2log6+3log6=( )
A. log6 B. 2 C. 0 D. 1
D
解析 2log6+3log6=log62+log63=log66=1,故选D.
评价反馈
3. 若lg 2=a,lg 3=b,则log125=( )
A. B. C. D.
C
解析 log125=.故选C.
评价反馈
4. 若logm2=a,logm3=b,则ma+2b的值为 .
18
解析 因为logm2=a,logm3=b,所以ma=2,mb=3,即ma+2b=ma×(mb)2=2×32=18.
评价反馈
5. 求值:2log32log3log38.
解 2log32log3log38
log34log3log383
log3(4××8)3
log393
=23
1.
课堂小结
本节课我们主要学习了哪些内容
1. 对数的运算性质.
2. 对数换底公式.
3. 对数运算性质的综合运用,应掌握变形技巧:
(1)各部分变形要化到最简形式,同时注意分子、分母的联系.
(2)要避免错用对数运算性质.
布置作业
完成教材第127页习题4.3第3,4,5题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
