第四章 4.4.3不同函数增长的差异--人教A版高中数学必修第一册教学课件(共34张PPT)
文档属性
| 名称 | 第四章 4.4.3不同函数增长的差异--人教A版高中数学必修第一册教学课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:37:36 | ||
图片预览







文档简介
(共34张PPT)
4.4.3 不同函数增长的差异
第四章 指数函数与对数函数
数学
学习目标
①结合具体函数图象,总结一次函数、指数函数、对数函数的增长差异.
②通过图象,了解“直线上升”“对数增长”“指数爆炸”的含义.
学习重难点
重点:
函数增长快慢比较的常用方法.
难点:
了解影响函数增长快慢的因素.
课堂导入
情境1
有人说,一张普通的报纸对折30次后,厚度会超过10座珠穆朗玛峰的高度,会是真的吗
真
课堂导入
情境2
“陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子,在第二个小格内给两粒,第三格内给四粒,用这样下去,每一小格内都比前一小格加一倍.陛下,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧! ”
“爱卿,你所求的并不多啊!”
假
课堂探究
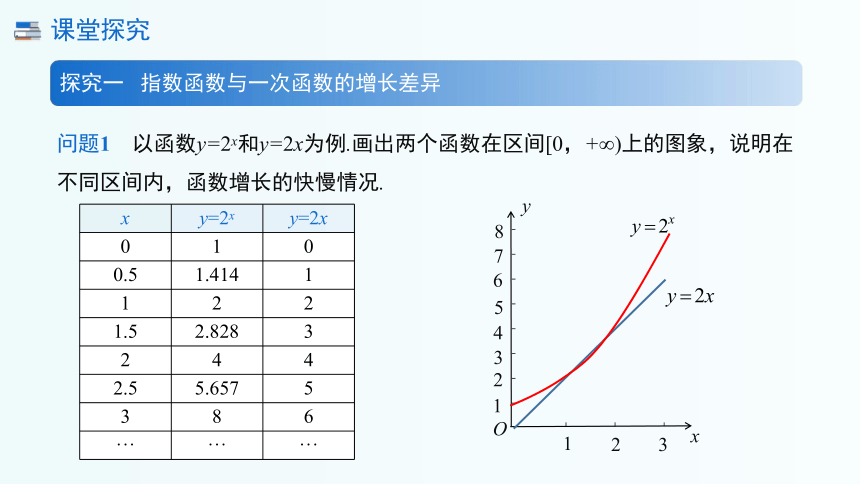
问题1 以函数y=2x和y=2x为例.画出两个函数在区间[0,+∞)上的图象,说明在不同区间内,函数增长的快慢情况.
x y=2x y=2x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
x
1
3
2
y
8
O
5
1
2
3
7
6
4
探究一 指数函数与一次函数的增长差异
课堂探究
x
1
3
2
y
8
O
5
1
2
3
7
6
4
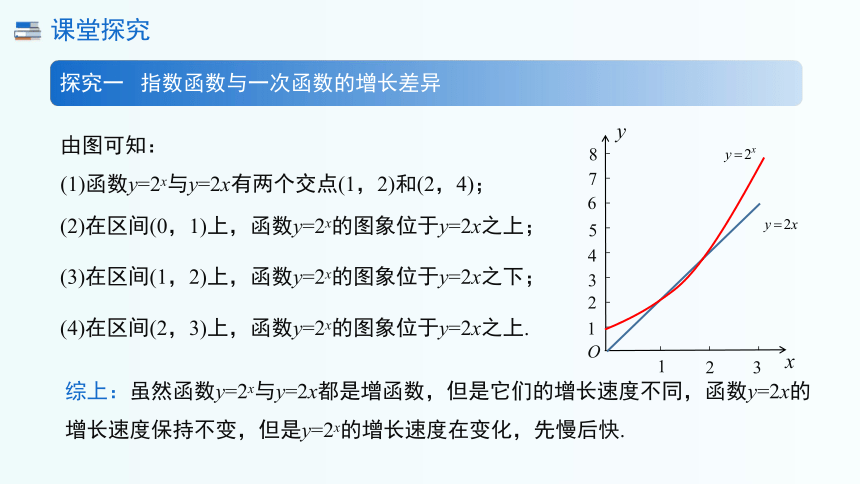
由图可知:
(1)函数y=2x与y=2x有两个交点(1,2)和(2,4);
(2)在区间(0,1)上,函数y=2x的图象位于y=2x之上;
(3)在区间(1,2)上,函数y=2x的图象位于y=2x之下;
(4)在区间(2,3)上,函数y=2x的图象位于y=2x之上.
综上:虽然函数y=2x与y=2x都是增函数,但是它们的增长速度不同,函数y=2x的增长速度保持不变,但是y=2x的增长速度在变化,先慢后快.
探究一 指数函数与一次函数的增长差异
课堂探究
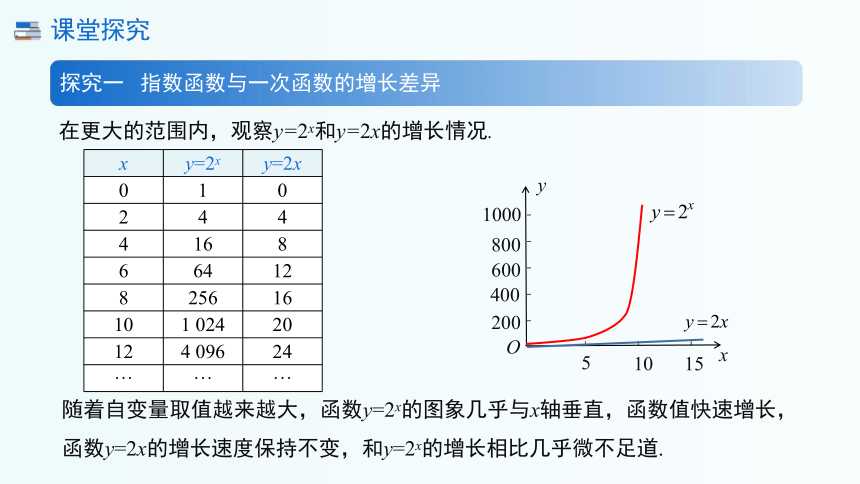
在更大的范围内,观察y=2x和y=2x的增长情况.
x y=2x y=2x
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1 024 20
12 4 096 24
··· ··· ···
x
5
15
10
y
O
1000
200
400
600
800
随着自变量取值越来越大,函数y=2x的图象几乎与x轴垂直,函数值快速增长,函数y=2x的增长速度保持不变,和y=2x的增长相比几乎微不足道.
探究一 指数函数与一次函数的增长差异
课堂探究
函数y=2x与y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数y=2x与y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
尽管在x的一定范围内,2x<2x,但由于y=2x的增长最终会快于y=2x的增长,因此,总会存在一个x0,当x>x0时,恒有2x>2x.
探究一 指数函数与一次函数的增长差异
课堂探究
一般地,指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长都与上述类似.
即使k值远远大于a值,指数函数y=ax(a>1) 有一段区间会小于y=kx(k>0),但总会存在一个x0,当x>x0时,y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.
探究一 指数函数与一次函数的增长差异
课堂探究
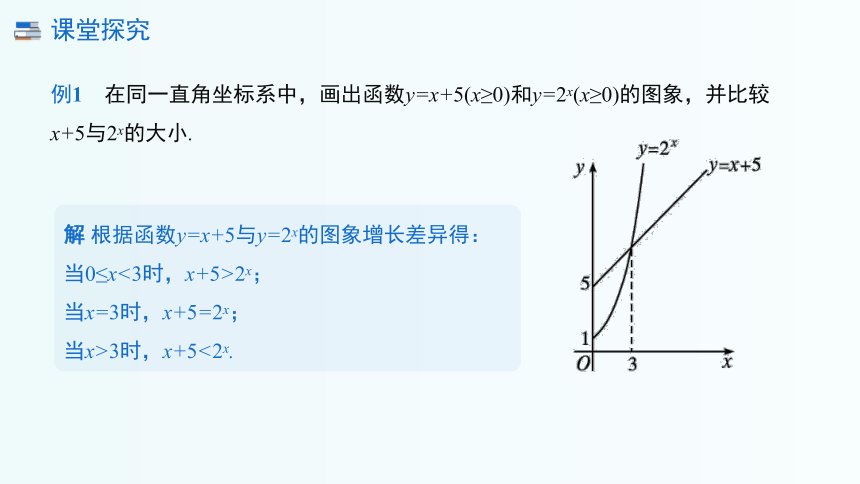
例1 在同一直角坐标系中,画出函数y=x+5(x≥0)和y=2x(x≥0)的图象,并比较x+5与2x的大小.
解 根据函数y=x+5与y=2x的图象增长差异得:
当0≤x<3时,x+5>2x;
当x=3时,x+5=2x;
当x>3时,x+5<2x.
课堂探究
规律方法
(1)线性函数模型
线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
(2)指数函数模型
指数型函数模型y==abx+c(a,b,c为常数,a>0,b>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,
即增长速度急剧,形象地称为“指数爆炸”.
课堂探究
【跟踪训练1】
(多选题)若函数y1=x2,y2=2x,y3=x,则下列关于这三个函数的描述正确的是( )
A.随着x的逐渐增大,y1增长速度越来越快于y2
B.随着x的逐渐增大,y2增长速度越来越快于y1
C.当x∈(0,+∞)时,y1增长速度一直快于y3
D.当x∈(0,+∞)时,y2增长速度有时快于y1
解析 在同一直角坐标系内画出函数y1=x2,y2=2x,y3=x的图象,如图.
对于A,随着x的逐渐增大,y1增长速度不是越来越快于y2,所以A错误;
对于B,随着x的逐渐增大,y2增长速度越来越快于y1,所以B正确;
对于C,当x∈(0,+∞)时,y1增长速度不是一直快于y3,所以C错误;
对于D,当x∈(0,+∞)时,y2增长速度有时快于y1,所以D正确.故选BD.
BD
课堂探究
问题2 以函数y=lg x和函数y=x为例,画出两个函数的图象,说明在不同区间内,函数增长的快慢情况.
x y=lg x
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
x
20
40
30
y
O
6
1
2
3
4
5
10
60
50
探究二 对数函数与一次函数的增长差异
课堂探究
虽然它们在(0,+∞)上都单调递增,但增长速度存在着明显的差异.函数y=x的增长速度保持不变,而y=lg x的增长速度在变化.随着x的增大,函数y=x的图象离x轴越来越远,而函数y=lg x的图象越来越平缓,就像与x轴平行一样.
例如lg 10=1,lg 100=2,lg 1 000=3,lg 10 000=4;而×10=1,×100=10,×1 000=100,×10 000=1 000.这说明,当x>10,即y=lg x>lg 10=1时,y=lg x与y=x相比增长得就很慢了.
探究二 对数函数与一次函数的增长差异
x
20
40
30
y
O
6
1
2
3
4
5
10
60
50
课堂探究
追问:将y=lg x放大1 000倍,将函数y=1 000lg x与比较,仍有上面规律吗
探究二 对数函数与一次函数的增长差异
课堂探究
一般地,虽然对数函数y=logax(a>1)与一次函数y=kx(k>0)在区间(0,+∞)上都单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数y=logax(a>1)的增长速度越来越慢.即使k的值很小,在一定范围内,logax可能会大于kx,但由于logax的增长最终会慢于kx的增长,因此总会存在一个x0,当x>x0时,恒有logax对数函数比较适合于描述增长速度平缓的变化规律.
探究二 对数函数与一次函数的增长差异
课堂探究
例2 函数f(x)=lg x,g(x)=0.3x 1的图象如图所示.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
解 (1)由函数图象特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x 1,曲线C2对应的函数为f(x)=lg x;
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)f(x);当x=x1或x=x2时,g(x)=f(x).
课堂探究
规律方法
对数函数模型:
能用对数型函数f(x)=mloga x+n(m,n,a为常数,m>0,x>0,a>1)表达的函数模型,其增长的特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓,常称之为“蜗牛式增长”.
课堂探究
【跟踪训练2】
(1)下列函数中,增长速度最慢的是( )
A. y=6x B. y=log6 x
C. y=x6 D. y=6x
解析 (1)比较可知对数函数的增长速度最慢.故选B.
B
课堂探究
【跟踪训练2】
(2)有一组数据如下表:
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A. v=log2 t B. v=lot C. v= D. v=2t 2
解析 (2)(方法1)从表格中数据可知此函数为单调递增函数,排除B,且增长速度越来越快,排除A和D,故选C.(方法2)作出散点图,如图所示.易知C满足题意,故选C.
C
t 1.99 3.0 4.0 5.1 6.12
v 1.5 4.04 7.5 12 18.01
课堂探究
探究三 函数模型的选择
例3 某汽车制造公司在2024年初公告:计划某型号汽车2024年生产目标定为43万辆.已知该公司近三年的该型号汽车年产量如下表所示.
年份 2021 2022 2023
年产量/万辆 8 18 30
如果我们分别将2021,2022,2023,2024年定义为第一、二、三、四年,现在有两个函数模型:二次函数模型f(x)=ax2+bx+c(a≠0),指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),哪个模型能更好地反映该公司该型号汽车年产量y与年份x的关系
课堂探究
解 建立年产量y与年份x的函数,可知函数图象过点(1,8),(2,18),(3,30).
①构造二次函数模型f(x)=ax2+bx+c(a≠0),将点的坐标代入,
可得解得则f(x)=x2+7x,
故f(4)=44,与计划误差为1万辆.
②构造指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),将点的坐标代入,
可得解得则g(x)=·()x 42,
故g(4)=×()4 42=44.4,与计划误差为1.4万辆.
由①②,可得二次函数模型f(x)=x2+7x能更好地反映该公司该型号汽车年产量y与年份x的关系.
课堂探究
规律方法
不同函数模型的选取标准:
(1)线性函数增长模型适合于描述增长速度不变的变化规律.
(2)指数函数增长模型适合于描述增长速度急剧的变化规律.
(3)对数函数增长模型适合于描述增长速度平缓的变化规律.
(4)幂函数增长模型适合于描述增长速度一般的变化规律.
评价反馈
1. 下列函数中,随x的增大而增长速度最快的是 ( )
A.y=ex B.y=ln x
C.y=x1 000 D.y=2x
解析 对数函数、幂函数、指数函数比较,指数函数的增长速度最快.
对于y=ex,y=2x,因为e>2,所以y=ex比y=2x增长速度快,
故选A.
A
评价反馈
2. 能使不等式log2xA.(0,+∞)
B.(2,+∞)
C.( ∞,2)
D.(0,2)∪(4,+∞)
解析 在同一平面直角坐标系内,作出这三个函数的图象,如图.由图象可知当x∈(0,2)∪(4,+∞)时,log2xD
评价反馈
3. 某大型超市为了满足顾客对商品的购物需求,对超市的商品种类做了一定的调整,结果调整初期利润增长迅速,随着时间的推移,增长速度越来越慢,如果建立恰当的函数模型来反映该超市调整后利润y与售出商品的数量x的关系,则可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
解析 四个函数中,A的增长速度不变,B,C增长速度越来越快,其中C增长速度比B更快,D增长速度越来越慢,故只有D能反映y与x的关系.
D
评价反馈
4. 下列选项是四种生意预期的收益y关于时间x的函数,从足够长远的角度看,更为有前途的生意是 (填序号).
①y=10×1.05x; ②y=20+x1.5;
③y=30+lg(x+1); ④y=50.
解析 比较所有函数的增长速度,易知选①.
①
评价反馈
5. 甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是 (填序号).
①甲比乙先出发;
②乙比甲跑的路程多;
③甲、乙两人的速度相同;
④甲比乙先到达终点.
解析 由题图知,甲、乙两人同时从t=0时开始赛跑,s与t的关系均为直线上升,路程s的增长速度不变,即甲、乙均为匀速运动,但甲的速度快.又甲、乙的路程s取值范围相同,即跑了相同的路程,但甲用时少,故先到终点.
④
评价反馈
6. 有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元,它们与投入资金m(单位:万元)的关系式为p=m,q=.今有3万元资金投入这两种商品.若设对甲种商品投资x万元,投资两种商品所获得的总利润为y万元.
(1)写出y关于x的函数表达式;
(2)如何分配资金可使获得的总利润最大 并求最大利润的值.
解 (1)由题意知,对甲种商品投资x万元,获得的总利润为y万元,
则对乙种商品的投资为(3 x)万元,
所以y=x+(0≤x≤3).
评价反馈
6. 有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元,它们与投入资金m(单位:万元)的关系式为p=m,q=.今有3万元资金投入这两种商品.若设对甲种商品投资x万元,投资两种商品所获得的总利润为y万元.
(1)写出y关于x的函数表达式;
(2)如何分配资金可使获得的总利润最大 并求最大利润的值.
(2)令t=(0≤t≤),则x=3 t2,所以y=(3 t2)+t= (t )2+,
所以当t=时,ymax==1.05(万元).由t=可求得x=0.75(万元),
3 x=2.25(万元),所以为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,此时获得的最大利润为1.05万元.
课堂导入
增函数
增函数
增函数
y轴
x轴
越来越快
越来越慢
知识归纳
布置作业
完成教材第139页练习第1,2,3,4题.
完成教材第140~141页习题4.4第3,4,10,11题.
谢谢大家
4.4.3 不同函数增长的差异
第四章 指数函数与对数函数
数学
学习目标
①结合具体函数图象,总结一次函数、指数函数、对数函数的增长差异.
②通过图象,了解“直线上升”“对数增长”“指数爆炸”的含义.
学习重难点
重点:
函数增长快慢比较的常用方法.
难点:
了解影响函数增长快慢的因素.
课堂导入
情境1
有人说,一张普通的报纸对折30次后,厚度会超过10座珠穆朗玛峰的高度,会是真的吗
真
课堂导入
情境2
“陛下,请您在这张棋盘的第一个小格内,赏给我一粒麦子,在第二个小格内给两粒,第三格内给四粒,用这样下去,每一小格内都比前一小格加一倍.陛下,把这样摆满棋盘上所有64格的麦粒,都赏给您的仆人吧! ”
“爱卿,你所求的并不多啊!”
假
课堂探究
问题1 以函数y=2x和y=2x为例.画出两个函数在区间[0,+∞)上的图象,说明在不同区间内,函数增长的快慢情况.
x y=2x y=2x
0 1 0
0.5 1.414 1
1 2 2
1.5 2.828 3
2 4 4
2.5 5.657 5
3 8 6
··· ··· ···
x
1
3
2
y
8
O
5
1
2
3
7
6
4
探究一 指数函数与一次函数的增长差异
课堂探究
x
1
3
2
y
8
O
5
1
2
3
7
6
4
由图可知:
(1)函数y=2x与y=2x有两个交点(1,2)和(2,4);
(2)在区间(0,1)上,函数y=2x的图象位于y=2x之上;
(3)在区间(1,2)上,函数y=2x的图象位于y=2x之下;
(4)在区间(2,3)上,函数y=2x的图象位于y=2x之上.
综上:虽然函数y=2x与y=2x都是增函数,但是它们的增长速度不同,函数y=2x的增长速度保持不变,但是y=2x的增长速度在变化,先慢后快.
探究一 指数函数与一次函数的增长差异
课堂探究
在更大的范围内,观察y=2x和y=2x的增长情况.
x y=2x y=2x
0 1 0
2 4 4
4 16 8
6 64 12
8 256 16
10 1 024 20
12 4 096 24
··· ··· ···
x
5
15
10
y
O
1000
200
400
600
800
随着自变量取值越来越大,函数y=2x的图象几乎与x轴垂直,函数值快速增长,函数y=2x的增长速度保持不变,和y=2x的增长相比几乎微不足道.
探究一 指数函数与一次函数的增长差异
课堂探究
函数y=2x与y=2x在[0,+∞)上增长快慢的不同如下:
虽然函数y=2x与y=2x在[0,+∞)上都是单调递增,但它们的增长速度不同.
随着x的增大,y=2x的增长速度越来越快,会超过并远远大于y=2x的增长速度.
尽管在x的一定范围内,2x<2x,但由于y=2x的增长最终会快于y=2x的增长,因此,总会存在一个x0,当x>x0时,恒有2x>2x.
探究一 指数函数与一次函数的增长差异
课堂探究
一般地,指数函数y=ax(a>1)与一次函数y=kx(k>0)的增长都与上述类似.
即使k值远远大于a值,指数函数y=ax(a>1) 有一段区间会小于y=kx(k>0),但总会存在一个x0,当x>x0时,y=ax(a>1)的增长速度会大大超过y=kx(k>0)的增长速度.
探究一 指数函数与一次函数的增长差异
课堂探究
例1 在同一直角坐标系中,画出函数y=x+5(x≥0)和y=2x(x≥0)的图象,并比较x+5与2x的大小.
解 根据函数y=x+5与y=2x的图象增长差异得:
当0≤x<3时,x+5>2x;
当x=3时,x+5=2x;
当x>3时,x+5<2x.
课堂探究
规律方法
(1)线性函数模型
线性函数模型y=kx+b(k>0)的增长特点是直线上升,其增长速度不变.
(2)指数函数模型
指数型函数模型y==abx+c(a,b,c为常数,a>0,b>1)的增长特点是随着自变量的增大,函数值增大的速度越来越快,
即增长速度急剧,形象地称为“指数爆炸”.
课堂探究
【跟踪训练1】
(多选题)若函数y1=x2,y2=2x,y3=x,则下列关于这三个函数的描述正确的是( )
A.随着x的逐渐增大,y1增长速度越来越快于y2
B.随着x的逐渐增大,y2增长速度越来越快于y1
C.当x∈(0,+∞)时,y1增长速度一直快于y3
D.当x∈(0,+∞)时,y2增长速度有时快于y1
解析 在同一直角坐标系内画出函数y1=x2,y2=2x,y3=x的图象,如图.
对于A,随着x的逐渐增大,y1增长速度不是越来越快于y2,所以A错误;
对于B,随着x的逐渐增大,y2增长速度越来越快于y1,所以B正确;
对于C,当x∈(0,+∞)时,y1增长速度不是一直快于y3,所以C错误;
对于D,当x∈(0,+∞)时,y2增长速度有时快于y1,所以D正确.故选BD.
BD
课堂探究
问题2 以函数y=lg x和函数y=x为例,画出两个函数的图象,说明在不同区间内,函数增长的快慢情况.
x y=lg x
0 不存在 0
10 1 1
20 1.301 2
30 1.477 3
40 1.602 4
50 1.699 5
60 1.778 6
··· ··· ···
x
20
40
30
y
O
6
1
2
3
4
5
10
60
50
探究二 对数函数与一次函数的增长差异
课堂探究
虽然它们在(0,+∞)上都单调递增,但增长速度存在着明显的差异.函数y=x的增长速度保持不变,而y=lg x的增长速度在变化.随着x的增大,函数y=x的图象离x轴越来越远,而函数y=lg x的图象越来越平缓,就像与x轴平行一样.
例如lg 10=1,lg 100=2,lg 1 000=3,lg 10 000=4;而×10=1,×100=10,×1 000=100,×10 000=1 000.这说明,当x>10,即y=lg x>lg 10=1时,y=lg x与y=x相比增长得就很慢了.
探究二 对数函数与一次函数的增长差异
x
20
40
30
y
O
6
1
2
3
4
5
10
60
50
课堂探究
追问:将y=lg x放大1 000倍,将函数y=1 000lg x与比较,仍有上面规律吗
探究二 对数函数与一次函数的增长差异
课堂探究
一般地,虽然对数函数y=logax(a>1)与一次函数y=kx(k>0)在区间(0,+∞)上都单调递增,但它们的增长速度不同.
随着x的增大,一次函数y=kx(k>0)保持固定的增长速度,而对数函数y=logax(a>1)的增长速度越来越慢.即使k的值很小,在一定范围内,logax可能会大于kx,但由于logax的增长最终会慢于kx的增长,因此总会存在一个x0,当x>x0时,恒有logax
探究二 对数函数与一次函数的增长差异
课堂探究
例2 函数f(x)=lg x,g(x)=0.3x 1的图象如图所示.
(1)试根据函数的增长差异指出曲线C1,C2分别对应的函数;
(2)比较两函数的增长差异(以两图象交点为分界点,对f(x),g(x)的大小进行比较).
解 (1)由函数图象特征及变化趋势,知曲线C1对应的函数为g(x)=0.3x 1,曲线C2对应的函数为f(x)=lg x;
(2)当x∈(0,x1)时,g(x)>f(x);当x∈(x1,x2)时,g(x)
课堂探究
规律方法
对数函数模型:
能用对数型函数f(x)=mloga x+n(m,n,a为常数,m>0,x>0,a>1)表达的函数模型,其增长的特点是随着自变量的增大,函数值增大的速度越来越慢,即增长速度平缓,常称之为“蜗牛式增长”.
课堂探究
【跟踪训练2】
(1)下列函数中,增长速度最慢的是( )
A. y=6x B. y=log6 x
C. y=x6 D. y=6x
解析 (1)比较可知对数函数的增长速度最慢.故选B.
B
课堂探究
【跟踪训练2】
(2)有一组数据如下表:
现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( )
A. v=log2 t B. v=lot C. v= D. v=2t 2
解析 (2)(方法1)从表格中数据可知此函数为单调递增函数,排除B,且增长速度越来越快,排除A和D,故选C.(方法2)作出散点图,如图所示.易知C满足题意,故选C.
C
t 1.99 3.0 4.0 5.1 6.12
v 1.5 4.04 7.5 12 18.01
课堂探究
探究三 函数模型的选择
例3 某汽车制造公司在2024年初公告:计划某型号汽车2024年生产目标定为43万辆.已知该公司近三年的该型号汽车年产量如下表所示.
年份 2021 2022 2023
年产量/万辆 8 18 30
如果我们分别将2021,2022,2023,2024年定义为第一、二、三、四年,现在有两个函数模型:二次函数模型f(x)=ax2+bx+c(a≠0),指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),哪个模型能更好地反映该公司该型号汽车年产量y与年份x的关系
课堂探究
解 建立年产量y与年份x的函数,可知函数图象过点(1,8),(2,18),(3,30).
①构造二次函数模型f(x)=ax2+bx+c(a≠0),将点的坐标代入,
可得解得则f(x)=x2+7x,
故f(4)=44,与计划误差为1万辆.
②构造指数函数模型g(x)=a·bx+c(a≠0,b>0,b≠1),将点的坐标代入,
可得解得则g(x)=·()x 42,
故g(4)=×()4 42=44.4,与计划误差为1.4万辆.
由①②,可得二次函数模型f(x)=x2+7x能更好地反映该公司该型号汽车年产量y与年份x的关系.
课堂探究
规律方法
不同函数模型的选取标准:
(1)线性函数增长模型适合于描述增长速度不变的变化规律.
(2)指数函数增长模型适合于描述增长速度急剧的变化规律.
(3)对数函数增长模型适合于描述增长速度平缓的变化规律.
(4)幂函数增长模型适合于描述增长速度一般的变化规律.
评价反馈
1. 下列函数中,随x的增大而增长速度最快的是 ( )
A.y=ex B.y=ln x
C.y=x1 000 D.y=2x
解析 对数函数、幂函数、指数函数比较,指数函数的增长速度最快.
对于y=ex,y=2x,因为e>2,所以y=ex比y=2x增长速度快,
故选A.
A
评价反馈
2. 能使不等式log2x
B.(2,+∞)
C.( ∞,2)
D.(0,2)∪(4,+∞)
解析 在同一平面直角坐标系内,作出这三个函数的图象,如图.由图象可知当x∈(0,2)∪(4,+∞)时,log2x
评价反馈
3. 某大型超市为了满足顾客对商品的购物需求,对超市的商品种类做了一定的调整,结果调整初期利润增长迅速,随着时间的推移,增长速度越来越慢,如果建立恰当的函数模型来反映该超市调整后利润y与售出商品的数量x的关系,则可选用( )
A.一次函数 B.二次函数
C.指数型函数 D.对数型函数
解析 四个函数中,A的增长速度不变,B,C增长速度越来越快,其中C增长速度比B更快,D增长速度越来越慢,故只有D能反映y与x的关系.
D
评价反馈
4. 下列选项是四种生意预期的收益y关于时间x的函数,从足够长远的角度看,更为有前途的生意是 (填序号).
①y=10×1.05x; ②y=20+x1.5;
③y=30+lg(x+1); ④y=50.
解析 比较所有函数的增长速度,易知选①.
①
评价反馈
5. 甲、乙两人在一次赛跑中,从同一地点出发,路程s与时间t的函数关系如图所示,则下列说法正确的是 (填序号).
①甲比乙先出发;
②乙比甲跑的路程多;
③甲、乙两人的速度相同;
④甲比乙先到达终点.
解析 由题图知,甲、乙两人同时从t=0时开始赛跑,s与t的关系均为直线上升,路程s的增长速度不变,即甲、乙均为匀速运动,但甲的速度快.又甲、乙的路程s取值范围相同,即跑了相同的路程,但甲用时少,故先到终点.
④
评价反馈
6. 有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元,它们与投入资金m(单位:万元)的关系式为p=m,q=.今有3万元资金投入这两种商品.若设对甲种商品投资x万元,投资两种商品所获得的总利润为y万元.
(1)写出y关于x的函数表达式;
(2)如何分配资金可使获得的总利润最大 并求最大利润的值.
解 (1)由题意知,对甲种商品投资x万元,获得的总利润为y万元,
则对乙种商品的投资为(3 x)万元,
所以y=x+(0≤x≤3).
评价反馈
6. 有甲、乙两种商品,经销这两种商品所能获得的利润分别是p万元和q万元,它们与投入资金m(单位:万元)的关系式为p=m,q=.今有3万元资金投入这两种商品.若设对甲种商品投资x万元,投资两种商品所获得的总利润为y万元.
(1)写出y关于x的函数表达式;
(2)如何分配资金可使获得的总利润最大 并求最大利润的值.
(2)令t=(0≤t≤),则x=3 t2,所以y=(3 t2)+t= (t )2+,
所以当t=时,ymax==1.05(万元).由t=可求得x=0.75(万元),
3 x=2.25(万元),所以为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,此时获得的最大利润为1.05万元.
课堂导入
增函数
增函数
增函数
y轴
x轴
越来越快
越来越慢
知识归纳
布置作业
完成教材第139页练习第1,2,3,4题.
完成教材第140~141页习题4.4第3,4,10,11题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
