第四章 4.5.1函数的零点与方程的解--人教A版高中数学必修第一册教学课件(共32张PPT)
文档属性
| 名称 | 第四章 4.5.1函数的零点与方程的解--人教A版高中数学必修第一册教学课件(共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:37:54 | ||
图片预览










文档简介
(共32张PPT)
4.5.1 函数的零点与方程的解
第四章 指数函数与对数函数
数学
学习目标
①了解函数的零点、方程的根、函数图象与轴的公共点的横坐标之间的联系.
②会借助函数零点存在定理判断函数的零点所在的大致区间.
③能借助函数单调性及图象判断零点的个数.
重点难点
重点:
函数零点与方程的解之间的关系;求函数零点的方法;利用函数零点存在定理确定连续函数零点的大致区间.
难点:
发现与理解方程的解与函数零点的关系;探究函数零点存在定理的认知过程.
课堂导入
情境1
中外历史上的方程求解
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座.虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.
约公元50~100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
九章算术
课堂导入
情境1
中外历史上的方程求解
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法.
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
课堂导入
情境1
中外历史上的方程求解
国外数学家对方程求解亦有很多研究.9世纪以后,先后发现了一次、二次、三次、四次方程的求解方法.
由于实际问题的需要,我们经常需要寻求函数y=f(x)的零点.
课堂探究
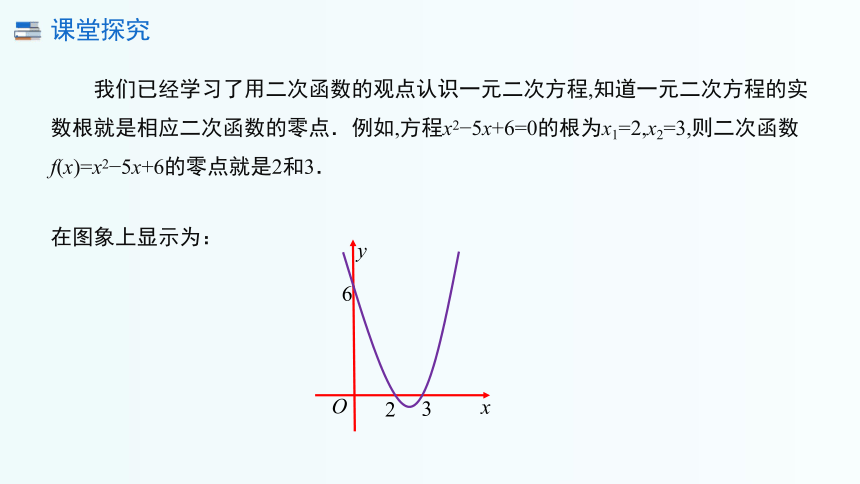
我们已经学习了用二次函数的观点认识一元二次方程,知道一元二次方程的实数根就是相应二次函数的零点.例如,方程x2 5x+6=0的根为x1=2,x2=3,则二次函数f(x)=x2 5x+6的零点就是2和3.
y
6
3
x
2
在图象上显示为:
O
课堂探究
画出下列函数的图象:
(1) f(x)=x1 f(x)=x22x+1 (2) f(x)= f(x)=
(3) f(x)=2x1 f(x)=log2x
当函数和x轴有交点时,其交点横坐标与方程 f(x)=0 的解有什么关系
再任意画几个函数的图象,观察其图象,看看其交点横坐标与相应方程 f(x)=0 的解有什么关系
课堂探究
探究一 函数的零点
零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的“零点”是点吗
提示:不是.函数y=f(x)的零点是方程f(x)=0的实数解,也就是函数y=f(x)的图象与x轴交点的横坐标.
等价关系:
方程f(x)=0有实数解函数y=f(x)的图象与x轴有交点函数y=f(x)有零点
课堂探究
【例题1】
根据零点的定义判断对错与填空.
(1)任何函数都有零点. ( )
(2)函数y=x2的零点是(2,0). ( )
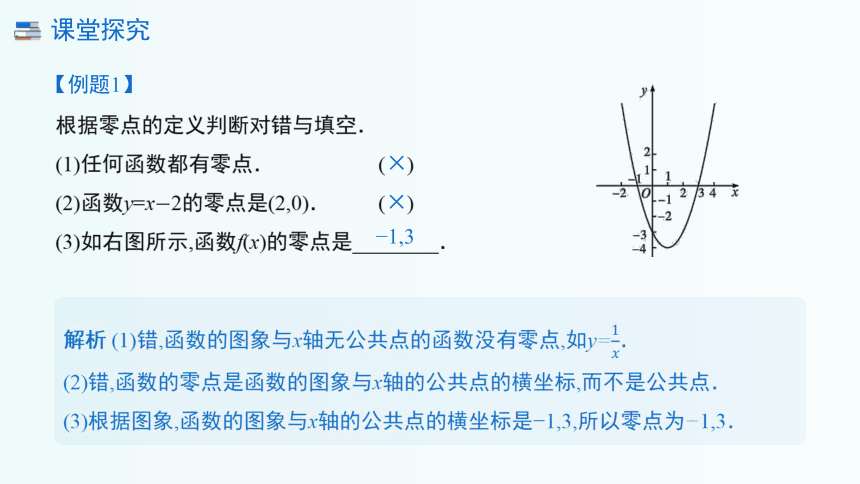
(3)如右图所示,函数f(x)的零点是________.
解析 (1)错,函数的图象与x轴无公共点的函数没有零点,如y=.
(2)错,函数的零点是函数的图象与x轴的公共点的横坐标,而不是公共点.
(3)根据图象,函数的图象与x轴的公共点的横坐标是 1,3,所以零点为 1,3.
×
×
1,3
课堂探究
归纳总结
函数零点的求法
求函数的零点通常有两种方法:
一是代数法,令f(x)=0,通过求方程f(x)=0的根求得函数的零点;
二是几何法,画出函数y=f(x)的图象,图象与x轴交点的横坐标即为函数的零点.
课堂探究
【跟踪训练1】
求下列函数的零点
(1)f(x)=2x+3;
(2)f(x)=2x 4.
解 (1)(方法1)函数f(x)=2x+3的零点就是使2x+3=0的实数x,求该函数的零点就是求方程2x+3=0的实数解.由2x+3=0,得x= ,
所以函数f(x)=2x+3的零点是x= .
(方法2)画出函数的图象,如图,函数的图象与x轴公共点的横坐标为 ,则函数f(x)=2x+3的零点为 .
课堂探究
【跟踪训练1】
求下列函数的零点
(1)f(x)=2x+3;
(2)f(x)=2x 4.
解 (2) (方法1)函数f(x)=2x 4的零点就是使2x 4=0的实数x,求该函数的零点就是求方程2x 4=0的实数解.由2x 4=0,得x=2,所以函数f(x)=2x 4的零点是x=2.
(方法2)画出函数的图象,如图,函数的图象与x轴公共点的横坐标为2,则函数f(x)=2x 4的零点为2.
课堂探究
探究二 函数零点存在定理
观察函数的图象并填空:
x
y
O
a
b
c
d
O
y
x
g
e
1. 在区间(a,b)上f(a)·f(b)_____0(“<”或“>”).在区间(a,b)上______(有/无)零点;
2. 在区间(b,c)上f(b)·f(c) _____ 0(“<”或“>”).在区间(b,c)上______(有/无)零点;
3. 在区间(c,d)上f(c)·f(d) _____ 0(“<”或”>”).在区间(c,d)上______(有/无)零点;
4. 在区间(e,g)上f(e)·f(g) _____ 0(“<”或”>”).在区间(e,g)上______(有/无)零点;
有
<
<
有
<
有
<
无
思考问题
在怎样的条件下,函数y=f(x)在区间[a,b]上存在零点
课堂探究
课堂探究
探究二 函数零点存在定理
零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内至少有一个有零点,
即存在c∈(a,b),使得f(c)=0,这个c就是方程f(x)=0的解.
定理要求具备两个条件:
①函数在区间[a,b]上的图象是一条连续不断的曲线;
② f (a)· f (b)<0.
课堂探究
探究二 函数零点存在定理
为什么强调“函数y=f(x)在区间[a,b]上的图象一条连续不断的曲线” 如果函数图象不连续,或者y=f(x)不满足f(a)·f(b) <0,那么零点存在性定理还成立吗
x
y
O
a
b
O
y
x
b
a
O
y
x
b
a
O
y
x
b
a
课堂探究
探究三 函数零点区间及零点个数的判断
(1)在下列区间中,函数f(x)=ex+4x 3的零点所在的区间为( )
A.( ,0) B.(0,) C.() D. ()
【例题2】
解析 (1)由指数函数和一次函数的性质,可知函数f(x)在定义域R上单调递增.因为f()= 2<0,f()= 1>0,所以f()f()<0,所以零点在区间()内.
C
x 3 2 1 0 1 2 3 4
f(x) 6 m 4 6 6 4 n 6
课堂探究
探究三 函数零点区间及零点个数的判断
(2)二次函数f(x)=ax2+bx+c的部分对应值如下表:
不求a,b,c的值,判断方程ax2+bx+c=0的两根所在的区间是( )
A. ( 3, 1),(2,4) B. ( 3, 1),( 1,1)
C. ( 1,1),(1,2) D. ( ∞, 3),(4,+∞)
【例题2】
(2)显然二次函数f(x)在定义域R上的图象是一条连续不断的曲线,且f( 3)=6>0,
f( 1)= 4<0,所以方程在区间( 3, 1)内必有实数根,又f(2)= 4<0,f(4)=6>0,所以在区间(2,4)内必有实数根,故选A.
A
课堂探究
归纳总结
判断单调函数零点所在区间的方法:
1. 先判断函数在区间上的图象是否为一条连续不断的曲线.
2. (1)代入:将区间端点值代入函数解析式求出函数值;
(2)判断:把所得的函数值相乘,并进行符号判断;
(3)结论:若符号为正且函数在该区间内是单调函数,则在该区间内无零点,
若符号为负且函数连续,则在该区间内至少有一个零点.
课堂探究
函数f(x)=ln x 的零点所在的大致区间是( )
A. (1,2) B. (2,3) C. (3,4) D. (e,+∞)
【跟踪训练2】
解析 由题意知,函数f(x)在定义域(0,+∞)上单调递增.
∵f(1)= 2<0,f(2)=ln 2 1<0,∴在区间(1,2)内f(x)无零点.
又f(3)=ln 3 >0,∴f(2)f(3)<0,∴f(x)在区间(2,3)内有零点.
∴f(x)在区间(3,4),(e,+∞)内均无零点.故选B.
B
课堂探究
(1)函数f(x)=的零点个数是( )
A. 3 B. 2 C. 1 D. 0
【例题3】
解析 (1)当x≤0时,
由f(x)=x2+2x 3=0,得x1= 3,x2=1(舍去);
当x>0时,由f(x)= 2+ln x=0,得x=e2.
故函数的零点个数是2.故选B.
B
课堂探究
(2)判定函数f(x)=ln x+x2 3的零点的个数.
【例题3】
解析 (方法1)∵f(1)=ln 1+12 3= 2<0,f(2)=ln 2+22 3=ln 2+1>0,
∴f(1)f(2)<0.
又f(x)=ln x+x2 3在区间(1,2)上的图象是一条连续不断的曲线,
∴f(x)在区间(1,2)上必有零点.
又f(x)在定义域(0,+∞)上是单调递增的,
∴零点只有一个.
课堂探究
(2)判定函数f(x)=ln x+x2 3的零点的个数.
【例题3】
解析 (方法2)函数f(x)=ln x+x2 3的零点个数,即为方程ln x+x2 3=0根的个数,即为函数y=ln x与y=3 x2的图象交点个数.
在同一直角坐标系中,作出两函数的图象(如图).
由图象知,函数y=3 x2与y=ln x的图象在x∈(0,+∞)
只有一个交点,从而方程ln x+x2 3=0有一个根,
即函数f(x)=ln x+x2 3有一个零点.
课堂探究
归纳总结
判断函数f(x)存在零点的3种方法:
(1)方程法:若方程f(x)=0的解可求或能判断解的个数,则可通过方程的解来判断函数是否存在零点或判断零点的个数.
(2)图象法:由f(x)=g(x) h(x)=0,得g(x)=h(x),在同一直角坐标系内作出y1=g(x)和y2=h(x)的图象,根据两个图象交点的个数来判定函数零点的个数.
(3)定理法:如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点.若函数y=f(x)在区间(a,b)上是单调函数,则函数f(x)在区间(a,b)内只有一个零点.
课堂探究
求函数f(x)=2x+lg(x+1)2零点的个数.
【跟踪训练3】
解 ∵f(0)=1+02=1<0,
f(1)=2+lg 22>0,
又f(x)=2x+lg(x+1)2在区间(1,+∞)上是单调递增函数,
∴f(x)在(0,1)上必定存在零点,且函数f(x)有且只有一个零点.
评价反馈
1. 函数y=ln x的零点是( )
A. (0,0) B. 0 C. 1 D. 不存在
C
2. 下列各图象表示的函数中,没有零点的是( )
D
评价反馈
3. 函数f(x)=2x 的零点所在的区间是( )
A. (1,+∞)
B. (,1)
C. ()
D. ()
B
4. 函数f(x)=x3 ()x的零点有 个.
1
评价反馈
5. 若函数y=ax2 x 1只有一个零点,求实数a的值.
解 当a=0时,该函数为y= x 1,显然该函数的图象与x轴只有一个公共点,即函数只有一个零点.
当a≠0时,函数y=ax2 x 1为二次函数,
因为函数y=ax2 x 1只有一个零点,
所以关于x的方程ax2 x 1=0有两个相等的实根,
所以Δ=1+4a=0,即a= .
综上可知,实数a的值为0或 .
课堂小结
本节课我们主要学习了哪些内容
1. 函数的零点
对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.
2. 方程、函数、函数图象之间的关系
方程f(x)=0有实数解 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
3. 函数零点的存在性定理
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
布置作业
完成教材第144页练习第1,2题;第155页习题4.5第2,3,7题.
谢谢大家
4.5.1 函数的零点与方程的解
第四章 指数函数与对数函数
数学
学习目标
①了解函数的零点、方程的根、函数图象与轴的公共点的横坐标之间的联系.
②会借助函数零点存在定理判断函数的零点所在的大致区间.
③能借助函数单调性及图象判断零点的个数.
重点难点
重点:
函数零点与方程的解之间的关系;求函数零点的方法;利用函数零点存在定理确定连续函数零点的大致区间.
难点:
发现与理解方程的解与函数零点的关系;探究函数零点存在定理的认知过程.
课堂导入
情境1
中外历史上的方程求解
在人类用智慧架设的无数座从未知通向已知的金桥中,方程的求解是其中璀璨的一座.虽然今天我们可以从教科书中了解各式各样方程的解法,但这一切却经历了相当漫长的岁月.
约公元50~100年编成的《九章算术》给出了一次方程、二次方程和正系数三次方程的求解方法.
九章算术
课堂导入
情境1
中外历史上的方程求解
13世纪,南宋数学家秦九韶给出了求任意次代数方程的正根的解法.
11世纪,北宋数学家贾宪给出了三次及三次以上的方程的解法.
课堂导入
情境1
中外历史上的方程求解
国外数学家对方程求解亦有很多研究.9世纪以后,先后发现了一次、二次、三次、四次方程的求解方法.
由于实际问题的需要,我们经常需要寻求函数y=f(x)的零点.
课堂探究
我们已经学习了用二次函数的观点认识一元二次方程,知道一元二次方程的实数根就是相应二次函数的零点.例如,方程x2 5x+6=0的根为x1=2,x2=3,则二次函数f(x)=x2 5x+6的零点就是2和3.
y
6
3
x
2
在图象上显示为:
O
课堂探究
画出下列函数的图象:
(1) f(x)=x1 f(x)=x22x+1 (2) f(x)= f(x)=
(3) f(x)=2x1 f(x)=log2x
当函数和x轴有交点时,其交点横坐标与方程 f(x)=0 的解有什么关系
再任意画几个函数的图象,观察其图象,看看其交点横坐标与相应方程 f(x)=0 的解有什么关系
课堂探究
探究一 函数的零点
零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
函数的“零点”是点吗
提示:不是.函数y=f(x)的零点是方程f(x)=0的实数解,也就是函数y=f(x)的图象与x轴交点的横坐标.
等价关系:
方程f(x)=0有实数解函数y=f(x)的图象与x轴有交点函数y=f(x)有零点
课堂探究
【例题1】
根据零点的定义判断对错与填空.
(1)任何函数都有零点. ( )
(2)函数y=x2的零点是(2,0). ( )
(3)如右图所示,函数f(x)的零点是________.
解析 (1)错,函数的图象与x轴无公共点的函数没有零点,如y=.
(2)错,函数的零点是函数的图象与x轴的公共点的横坐标,而不是公共点.
(3)根据图象,函数的图象与x轴的公共点的横坐标是 1,3,所以零点为 1,3.
×
×
1,3
课堂探究
归纳总结
函数零点的求法
求函数的零点通常有两种方法:
一是代数法,令f(x)=0,通过求方程f(x)=0的根求得函数的零点;
二是几何法,画出函数y=f(x)的图象,图象与x轴交点的横坐标即为函数的零点.
课堂探究
【跟踪训练1】
求下列函数的零点
(1)f(x)=2x+3;
(2)f(x)=2x 4.
解 (1)(方法1)函数f(x)=2x+3的零点就是使2x+3=0的实数x,求该函数的零点就是求方程2x+3=0的实数解.由2x+3=0,得x= ,
所以函数f(x)=2x+3的零点是x= .
(方法2)画出函数的图象,如图,函数的图象与x轴公共点的横坐标为 ,则函数f(x)=2x+3的零点为 .
课堂探究
【跟踪训练1】
求下列函数的零点
(1)f(x)=2x+3;
(2)f(x)=2x 4.
解 (2) (方法1)函数f(x)=2x 4的零点就是使2x 4=0的实数x,求该函数的零点就是求方程2x 4=0的实数解.由2x 4=0,得x=2,所以函数f(x)=2x 4的零点是x=2.
(方法2)画出函数的图象,如图,函数的图象与x轴公共点的横坐标为2,则函数f(x)=2x 4的零点为2.
课堂探究
探究二 函数零点存在定理
观察函数的图象并填空:
x
y
O
a
b
c
d
O
y
x
g
e
1. 在区间(a,b)上f(a)·f(b)_____0(“<”或“>”).在区间(a,b)上______(有/无)零点;
2. 在区间(b,c)上f(b)·f(c) _____ 0(“<”或“>”).在区间(b,c)上______(有/无)零点;
3. 在区间(c,d)上f(c)·f(d) _____ 0(“<”或”>”).在区间(c,d)上______(有/无)零点;
4. 在区间(e,g)上f(e)·f(g) _____ 0(“<”或”>”).在区间(e,g)上______(有/无)零点;
有
<
<
有
<
有
<
无
思考问题
在怎样的条件下,函数y=f(x)在区间[a,b]上存在零点
课堂探究
课堂探究
探究二 函数零点存在定理
零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内至少有一个有零点,
即存在c∈(a,b),使得f(c)=0,这个c就是方程f(x)=0的解.
定理要求具备两个条件:
①函数在区间[a,b]上的图象是一条连续不断的曲线;
② f (a)· f (b)<0.
课堂探究
探究二 函数零点存在定理
为什么强调“函数y=f(x)在区间[a,b]上的图象一条连续不断的曲线” 如果函数图象不连续,或者y=f(x)不满足f(a)·f(b) <0,那么零点存在性定理还成立吗
x
y
O
a
b
O
y
x
b
a
O
y
x
b
a
O
y
x
b
a
课堂探究
探究三 函数零点区间及零点个数的判断
(1)在下列区间中,函数f(x)=ex+4x 3的零点所在的区间为( )
A.( ,0) B.(0,) C.() D. ()
【例题2】
解析 (1)由指数函数和一次函数的性质,可知函数f(x)在定义域R上单调递增.因为f()= 2<0,f()= 1>0,所以f()f()<0,所以零点在区间()内.
C
x 3 2 1 0 1 2 3 4
f(x) 6 m 4 6 6 4 n 6
课堂探究
探究三 函数零点区间及零点个数的判断
(2)二次函数f(x)=ax2+bx+c的部分对应值如下表:
不求a,b,c的值,判断方程ax2+bx+c=0的两根所在的区间是( )
A. ( 3, 1),(2,4) B. ( 3, 1),( 1,1)
C. ( 1,1),(1,2) D. ( ∞, 3),(4,+∞)
【例题2】
(2)显然二次函数f(x)在定义域R上的图象是一条连续不断的曲线,且f( 3)=6>0,
f( 1)= 4<0,所以方程在区间( 3, 1)内必有实数根,又f(2)= 4<0,f(4)=6>0,所以在区间(2,4)内必有实数根,故选A.
A
课堂探究
归纳总结
判断单调函数零点所在区间的方法:
1. 先判断函数在区间上的图象是否为一条连续不断的曲线.
2. (1)代入:将区间端点值代入函数解析式求出函数值;
(2)判断:把所得的函数值相乘,并进行符号判断;
(3)结论:若符号为正且函数在该区间内是单调函数,则在该区间内无零点,
若符号为负且函数连续,则在该区间内至少有一个零点.
课堂探究
函数f(x)=ln x 的零点所在的大致区间是( )
A. (1,2) B. (2,3) C. (3,4) D. (e,+∞)
【跟踪训练2】
解析 由题意知,函数f(x)在定义域(0,+∞)上单调递增.
∵f(1)= 2<0,f(2)=ln 2 1<0,∴在区间(1,2)内f(x)无零点.
又f(3)=ln 3 >0,∴f(2)f(3)<0,∴f(x)在区间(2,3)内有零点.
∴f(x)在区间(3,4),(e,+∞)内均无零点.故选B.
B
课堂探究
(1)函数f(x)=的零点个数是( )
A. 3 B. 2 C. 1 D. 0
【例题3】
解析 (1)当x≤0时,
由f(x)=x2+2x 3=0,得x1= 3,x2=1(舍去);
当x>0时,由f(x)= 2+ln x=0,得x=e2.
故函数的零点个数是2.故选B.
B
课堂探究
(2)判定函数f(x)=ln x+x2 3的零点的个数.
【例题3】
解析 (方法1)∵f(1)=ln 1+12 3= 2<0,f(2)=ln 2+22 3=ln 2+1>0,
∴f(1)f(2)<0.
又f(x)=ln x+x2 3在区间(1,2)上的图象是一条连续不断的曲线,
∴f(x)在区间(1,2)上必有零点.
又f(x)在定义域(0,+∞)上是单调递增的,
∴零点只有一个.
课堂探究
(2)判定函数f(x)=ln x+x2 3的零点的个数.
【例题3】
解析 (方法2)函数f(x)=ln x+x2 3的零点个数,即为方程ln x+x2 3=0根的个数,即为函数y=ln x与y=3 x2的图象交点个数.
在同一直角坐标系中,作出两函数的图象(如图).
由图象知,函数y=3 x2与y=ln x的图象在x∈(0,+∞)
只有一个交点,从而方程ln x+x2 3=0有一个根,
即函数f(x)=ln x+x2 3有一个零点.
课堂探究
归纳总结
判断函数f(x)存在零点的3种方法:
(1)方程法:若方程f(x)=0的解可求或能判断解的个数,则可通过方程的解来判断函数是否存在零点或判断零点的个数.
(2)图象法:由f(x)=g(x) h(x)=0,得g(x)=h(x),在同一直角坐标系内作出y1=g(x)和y2=h(x)的图象,根据两个图象交点的个数来判定函数零点的个数.
(3)定理法:如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,且有f(a)f(b)<0,那么,函数y=f(x)在区间(a,b)内至少有一个零点.若函数y=f(x)在区间(a,b)上是单调函数,则函数f(x)在区间(a,b)内只有一个零点.
课堂探究
求函数f(x)=2x+lg(x+1)2零点的个数.
【跟踪训练3】
解 ∵f(0)=1+02=1<0,
f(1)=2+lg 22>0,
又f(x)=2x+lg(x+1)2在区间(1,+∞)上是单调递增函数,
∴f(x)在(0,1)上必定存在零点,且函数f(x)有且只有一个零点.
评价反馈
1. 函数y=ln x的零点是( )
A. (0,0) B. 0 C. 1 D. 不存在
C
2. 下列各图象表示的函数中,没有零点的是( )
D
评价反馈
3. 函数f(x)=2x 的零点所在的区间是( )
A. (1,+∞)
B. (,1)
C. ()
D. ()
B
4. 函数f(x)=x3 ()x的零点有 个.
1
评价反馈
5. 若函数y=ax2 x 1只有一个零点,求实数a的值.
解 当a=0时,该函数为y= x 1,显然该函数的图象与x轴只有一个公共点,即函数只有一个零点.
当a≠0时,函数y=ax2 x 1为二次函数,
因为函数y=ax2 x 1只有一个零点,
所以关于x的方程ax2 x 1=0有两个相等的实根,
所以Δ=1+4a=0,即a= .
综上可知,实数a的值为0或 .
课堂小结
本节课我们主要学习了哪些内容
1. 函数的零点
对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.
2. 方程、函数、函数图象之间的关系
方程f(x)=0有实数解 函数y=f(x)的图象与x轴有交点 函数y=f(x)有零点.
3. 函数零点的存在性定理
如果函数y=f(x)在区间[a,b]上的图象是一条连续不断的曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
布置作业
完成教材第144页练习第1,2题;第155页习题4.5第2,3,7题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
