第四章 4.5.3函数模型的应用--人教A版高中数学必修第一册教学课件(共43张PPT)
文档属性
| 名称 | 第四章 4.5.3函数模型的应用--人教A版高中数学必修第一册教学课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:38:13 | ||
图片预览









文档简介
(共43张PPT)
4.5.3
函数模型的应用
第四章 指数函数与对数函数
数学
学习目标
① 会利用已知函数模型解决实际问题.
② 能建立函数模型解决实际问题.
③了解拟合函数模型并解决实际问题.
④认识函数概念模型的作用,提高数学建模、数据分析核心素养.
学习重难点
重点:
用函数建立数学模型解决实际问题的基本过程.
难点:
选择恰当的函数模型分析和解决实际问题.
课堂导入
情境
复利,是指在计算利息时,某一计息周期的利息是由本金加上先前周期所积累利息总额来计算的计息方式.
按复利计算利率的一种储蓄,本金为a元,每期的利率为r,设本利和为y,存期为x,要知道存一定期限之后所得的本利和,就要写出本利和y随着存期x变化的函数式.
假设存入的本金为1 000元,每期的利率为2.25%.
课堂导入
问题
思考1 五期后的本利和是多少
解决这一问题,
首先要建立一个指数函数关系式,
即y=a(1+r)x,
将相应的数据代入该关系式就可得到五期后的本利和.
课堂导入
思考2 (1)实际问题中两个变量之间一定是确定的函数关系吗
(2)函数模型中,要求定义域只需使函数式有意义就可以吗?
(3)用函数模型预测的结果和实际结果必须相等吗?
两个变量之间可以有关系,但不一定是确定的函数关系.
函数模型中定义域必须满足实际意义.
拟合函数预测的结果近似地符合实际结果即可.
问题
课堂探究
探究一 常见的函数模型
常 用 函 数 模 型 (1)一次函数模型
(2)二次函数模型
(3)指数函数模型
(4)对数函数模型
(5)幂函数模型
(6)分段函数模型
课堂探究
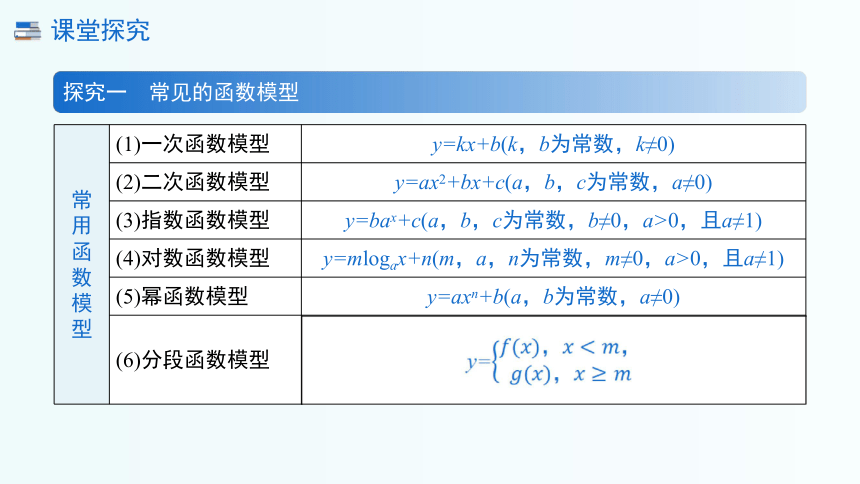
探究一 常见的函数模型
常 用 函 数 模 型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0,且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0,且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数模型
课堂探究
探究二 应用函数模型解决问题的基本过程
解答函数实际应用问题的步骤:
(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;
(3)求模——求解数学模型,得出数学模型的解;
(4)还原——将数学结论还原为实际问题.
注意:要判断取得最值时的自变量与实际意义是否相符.
课堂探究
1.判断(正确的画“√”,错误的画“×”)
(1)在一次函数模型中,系数k的取值会影响函数的性质. ( )
(2)在幂函数模型的解析式中,a的正负会影响函数的单调性. ( )
√
√
【小试牛刀】
课堂探究
2.某自行车存车处在某一天总共存放车辆4 000辆次,存车费为:电动车每辆一次0.3元,自行车每辆一次0.2元.若该天自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4 000)
B.y=0.5x(0≤x≤4 000)
C.y= 0.1x+1 200(0≤x≤4 000)
D.y=0.1x+1 200(0≤x≤4 000)
C
【小试牛刀】
课堂探究
3.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……现有2个这样的细胞,分裂x次后得到细胞的个数y与x的函数关系是( )
A.y=2x B.y=2x 1
C.y=2x D.y=2x+1
D
【小试牛刀】
课堂探究
4.若某物体一天内的温度T(单位:℃)是时间t(单位:h)的函数:T(t)=t3 3t+60,t=0时表示中午12:00,则上午8:00时的温度为 ℃.
8
【小试牛刀】
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(1)写出y关于x的函数解析式;
探究三 已知函数模型解决实际问题
解 (1)当x=1时,y=100+100×1.2%=100(1+1.2%);
当x=2时,y=100(1+1.2%)+100(1+1.2%)×1.2%=100(1+1.2%)2;
当x=3时,y=100(1+1.2%)2+100(1+1.2%)2×1.2%=100(1+1.2%)3;….
故y关于x的函数解析式为y=100(1+1.2%)x(x∈N*).
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(2)计算10年后该县的人口总数(精确到0.1万人);
探究三 已知函数模型解决实际问题
(2)当x=10时,y=100×(1+1.2%)10=100×1.01210≈112.7.
故10年后该县约有112.7万人.
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(3)计算大约多少年后该县的人口总数将达到120万(精确到1年).
探究三 已知函数模型解决实际问题
(3)设x年后该县的人口总数为120万,
即100×(1+1.2%)x=120,
解得x=log1.012≈15.3.
根据实际意义,大约16年后该县的人口总数将达到120万.
课堂探究
规律方法
1.指数函数模型
在实际问题中,有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数型函数模型表示,
通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.
课堂探究
规律方法
2.对数函数模型
有关对数型函数的应用题一般都会给出函数关系式,要求根据实际情况求出函数关系式中的参数,或给出具体情境,从中提炼出数据,代入关系式求值,然后根据所求值回答其实际意义.
课堂探究
规律方法
3.已知函数模型解决实际问题
往往给出的函数解析式含有参数,
需要将题中的数据代入函数模型,求得函数模型中的参数,
再将问题转化为已知函数解析式求函数值或自变量的值.
【跟踪训练1】
我们知道,燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度(单位:m/s)可以表示为函数v=5log2,其中Q表示燕子的耗氧量.计算:
(1)当燕子静止时的耗氧量是多少个单位
(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少
课堂探究
解 (1)由题意知,当燕子静止时,它的速度v=0,
代入题中公式,可得0=5log2,解得Q=10个单位.
(2)将耗氧量Q=80代入题中公式,得v=5log2=5log28=15(m/s).
课堂探究
例2 某市“网约车”的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0探究四 建立适当的函数模型解决实际问题
解 (1)由题意得车费f(x)关于路程x的函数为
f(x)=即f(x)=
课堂探究
例2 某市“网约车”的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
(2)某乘客的行程为16 km,他准备先乘一辆“网约车”行驶8 km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱 请说明理由.
探究四 建立适当的函数模型解决实际问题
(2)只乘一辆车的车费为f(16)=2.85×16 5.3=40.3(元),
换乘2辆车的车费为2f(8)=2×(4.2+1.9×8)=38.8(元).
因为40.3>38.8,所以该乘客换乘比只乘一辆车更省钱.
课堂探究
规律方法
1.一次函数模型的应用
利用一次函数求最值,常转化为求解不等式(或).
解答时,注意系数的正负,
也可以结合函数图象或其单调性来求最值.
课堂探究
规律方法
2.利用二次函数求最值的方法及注意点
方法:根据实际问题建立函数模型解析式后,
可利用配方法、判别式法、换元法及利用函数的单调性等方法求最值,
从而解决实际问题中的利润最大、用料最省等最值问题.
注意:取得最值时的自变量与实际意义是否相符.
课堂探究
规律方法
3.应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后比较再下结论.
【跟踪训练2】
某车间生产一种仪器的固定成本为10 000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=
其中x是仪器的月产量. (总收入=总成本+利润)
(1)将利润表示为月产量的函数(用f(x)表示);
课堂探究
解 (1)设总成本为t,则t=10 000+100x.
因为f(x)=H(x) t,
所以f(x)=
【跟踪训练2】
某车间生产一种仪器的固定成本为10 000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=
其中x是仪器的月产量. (总收入=总成本+利润)
(2)当月产量为何值时,车间所获利润最大 最大利润为多少元
课堂探究
(2)当0≤x≤200时,f(x)= (x 150)2+12 500,
所以当x=150时,有最大值12 500;
当x>200时,f(x)=30 000 100x是减函数,f(x)<30 000 100×200<12 500.
所以当x=150时,f(x)取得最大值,最大值为12 500.
所以当每月生产150台仪器时,利润最大,最大利润为12 500元.
课堂探究
例3 某纪念章从2024年6月1日起开始上市.通过市场调查,得到该纪念章每枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
(1)根据上表数据结合散点图,从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由:
①y=ax+b;②y=ax2+bx+c;③y=alogbx;
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
探究五 根据拟合效果选择恰当的函数模型解决实际问题
上市时间x天 4 10 36
市场价y元 90 51 90
课堂探究
解 (1)∵随着时间x的增加,y的值先减后增,而所给的三个函数中y=ax+b和y=alogbx显然都是单调函数,不满足题意,
∴用函数y=ax2+bx+c描述该纪念章的市场价y与上市时间x的变化关系.
(2)把点(4,90),(10,51),(36,90)的坐标分别代入y=ax2+bx+c中,
得解得
∴y=x2 10x+126=(x 20)2+26.
∴当x=20时,y有最小值26.
故该纪念章市场价最低时的上市天数为20天,最低的价格为26元.
课堂探究
规律方法
建立函数模型应遵循的三个原则
简化原则:建立函数模型,原型一定要简化,抓主要因素、主要变量,尽量建立较低阶、较简便的模型.
可推演原则:建立模型,一定要有意义,既能做理论分析,又能计算、推理,且能得出正确结论.
反映性原则:建立模型,应与原型具有“相似性”,所得模型的解应具有说明问题的功能,能回到具体问题中解决问题.
【跟踪训练3】
芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10 kg)与上市时间t(单位:天)的数据情况如表:
(1)根据表中数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt,并说明理由;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
课堂探究
t 50 110 250
Q 150 108 150
课堂探究
解 (1)由所提供的数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常数函数,若用函数Q=at+b,Q=a·bt,Q=alogbt中的任意一个来反映时都应有a≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q=at2+bt+c进行描述.
将表格所提供的三组数据分别代入函数Q=at2+bt+c,
可得解得a=,b= ,c=.
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数Q=t2 t+.
(2)当t= =150(天)时,芦荟种植成本最低为Q=×1502 ×150+=100(元/10 kg).
评价反馈
解析 由题中图象知,在不同时段内,路程折线图不同,
故对应的函数模型为分段函数.
1. 如果一辆汽车在某段路途中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数
B.二次函数
C.指数型函数
D.对数型函数
A
评价反馈
解析 当x=1时,由3 000=alog3(1+2),得a=3 000,
所以到2026年冬,即第7年,y=3 000×log3(7+2)=6 000.故选C.
2. 据统计,每年到鄱阳湖国家湿地公园越冬的白鹤数量y(单位:只)与时间x(单位:年)近似满足关系y=alog3(x+2),观测发现2020年冬(作为第1年)有越冬白鹤3 000只,估计到2026年冬有越冬白鹤( )
A.4 000只 B.5 000只
C.6 000只 D.7 000只
C
评价反馈
解析 设甲地销售x辆,则乙地销售(15 x)辆,
从而总利润为S=(5.06x 0.15x2)+2(15 x)= 0.15x2+3.06x+30(0≤x≤15,x∈N).
显然,当x=10时,S取得最大值S=45.6. 故选B.
3. 某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x 0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606 B.45.6
C.45.56 D.45.51
B
评价反馈
解析 由平均增长率的定义可知,(1+x)20=4.故选D.
4. 某工厂引进先进生产技术,产品产量从2023年1月到2024年8月的20个月间翻了两番,设月平均增长率为x,则有( )
A.(1+x)19=4 B.(1+x)20=3
C.(1+x)20=2 D.(1+x)20=4
D
评价反馈
5. 某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
则下列函数模型中,能较好地反映计算机在第x天被感染的数量y与x之间的关系的是( )
A.y=10x B.y=5x2 5x+10
C.y=10log2x+10 D.y=5×2x
D
第x天 1 2 3 4 5
被感染的计算机数量y/台 10 20 39 81 160
评价反馈
解析 对于A选项,当x=1,2,3,4,5时,对应的y值分别为10,20,30,40,50;对于B选项,当x=1,2,3,4,5时,对应的y值分别为10,20,40,70,110;对于C选项,当x=1,2,3,4,5时,对应的y值分别为10,20,10+10log23,30,10+10log25;对于D选项,当x=1,2,3,4,5时,对应的y值分别为10,20,40,80,160.而表中所给的数据当x=1,2,3,4,5时,对应的y值分别为10,20,39,81,160,通过比较,即可发现选项D中y的值误差最小,即y=5×2x能较好地反映y与x之间的关系,故选D.
评价反馈
解析 将x=3分别代入y=x2+1及y=3x 1中,
得y=32+1=10,y=3×3 1=8.
因为10更接近10.2,
所以选用甲模型.
6. 现测得(x,y)的两组对应值分别为(1,2),(2,5),现有两个待选模型,
甲:y=x2+1,乙:y=3x 1,若又测得(x,y)的一组对应值为(3,10.2),
则应选用 作为函数模型.
甲
课堂小结
知识构建
课堂小结
问题思考
(1)通过这节课,你学到了什么知识
(2)在解决问题时,用到了哪些数学思想
布置作业
完成教材第154页练习第1,2题;第155页习题4.5第6,8,9题.
谢谢大家
4.5.3
函数模型的应用
第四章 指数函数与对数函数
数学
学习目标
① 会利用已知函数模型解决实际问题.
② 能建立函数模型解决实际问题.
③了解拟合函数模型并解决实际问题.
④认识函数概念模型的作用,提高数学建模、数据分析核心素养.
学习重难点
重点:
用函数建立数学模型解决实际问题的基本过程.
难点:
选择恰当的函数模型分析和解决实际问题.
课堂导入
情境
复利,是指在计算利息时,某一计息周期的利息是由本金加上先前周期所积累利息总额来计算的计息方式.
按复利计算利率的一种储蓄,本金为a元,每期的利率为r,设本利和为y,存期为x,要知道存一定期限之后所得的本利和,就要写出本利和y随着存期x变化的函数式.
假设存入的本金为1 000元,每期的利率为2.25%.
课堂导入
问题
思考1 五期后的本利和是多少
解决这一问题,
首先要建立一个指数函数关系式,
即y=a(1+r)x,
将相应的数据代入该关系式就可得到五期后的本利和.
课堂导入
思考2 (1)实际问题中两个变量之间一定是确定的函数关系吗
(2)函数模型中,要求定义域只需使函数式有意义就可以吗?
(3)用函数模型预测的结果和实际结果必须相等吗?
两个变量之间可以有关系,但不一定是确定的函数关系.
函数模型中定义域必须满足实际意义.
拟合函数预测的结果近似地符合实际结果即可.
问题
课堂探究
探究一 常见的函数模型
常 用 函 数 模 型 (1)一次函数模型
(2)二次函数模型
(3)指数函数模型
(4)对数函数模型
(5)幂函数模型
(6)分段函数模型
课堂探究
探究一 常见的函数模型
常 用 函 数 模 型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0,且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0,且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数模型
课堂探究
探究二 应用函数模型解决问题的基本过程
解答函数实际应用问题的步骤:
(1)审题——弄清题意,分清条件和结论,理顺数量关系,初步选择模型;
(2)建模——将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识建立相应的数学模型;
(3)求模——求解数学模型,得出数学模型的解;
(4)还原——将数学结论还原为实际问题.
注意:要判断取得最值时的自变量与实际意义是否相符.
课堂探究
1.判断(正确的画“√”,错误的画“×”)
(1)在一次函数模型中,系数k的取值会影响函数的性质. ( )
(2)在幂函数模型的解析式中,a的正负会影响函数的单调性. ( )
√
√
【小试牛刀】
课堂探究
2.某自行车存车处在某一天总共存放车辆4 000辆次,存车费为:电动车每辆一次0.3元,自行车每辆一次0.2元.若该天自行车存车x辆次,存车费总收入为y元,则y与x的函数关系式为( )
A.y=0.2x(0≤x≤4 000)
B.y=0.5x(0≤x≤4 000)
C.y= 0.1x+1 200(0≤x≤4 000)
D.y=0.1x+1 200(0≤x≤4 000)
C
【小试牛刀】
课堂探究
3.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,……现有2个这样的细胞,分裂x次后得到细胞的个数y与x的函数关系是( )
A.y=2x B.y=2x 1
C.y=2x D.y=2x+1
D
【小试牛刀】
课堂探究
4.若某物体一天内的温度T(单位:℃)是时间t(单位:h)的函数:T(t)=t3 3t+60,t=0时表示中午12:00,则上午8:00时的温度为 ℃.
8
【小试牛刀】
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(1)写出y关于x的函数解析式;
探究三 已知函数模型解决实际问题
解 (1)当x=1时,y=100+100×1.2%=100(1+1.2%);
当x=2时,y=100(1+1.2%)+100(1+1.2%)×1.2%=100(1+1.2%)2;
当x=3时,y=100(1+1.2%)2+100(1+1.2%)2×1.2%=100(1+1.2%)3;….
故y关于x的函数解析式为y=100(1+1.2%)x(x∈N*).
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(2)计算10年后该县的人口总数(精确到0.1万人);
探究三 已知函数模型解决实际问题
(2)当x=10时,y=100×(1+1.2%)10=100×1.01210≈112.7.
故10年后该县约有112.7万人.
课堂探究
例1 目前某县有100万人,经过x年后为y万人.如果年平均增长率是1.2%,请回答下列问题:(参考数据:1.01210≈1.126 7,1.01211≈1.140 2,log1.0121.2≈15.3)
(3)计算大约多少年后该县的人口总数将达到120万(精确到1年).
探究三 已知函数模型解决实际问题
(3)设x年后该县的人口总数为120万,
即100×(1+1.2%)x=120,
解得x=log1.012≈15.3.
根据实际意义,大约16年后该县的人口总数将达到120万.
课堂探究
规律方法
1.指数函数模型
在实际问题中,有关人口增长、银行复利、细胞分裂等增长率问题常可以用指数型函数模型表示,
通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.
课堂探究
规律方法
2.对数函数模型
有关对数型函数的应用题一般都会给出函数关系式,要求根据实际情况求出函数关系式中的参数,或给出具体情境,从中提炼出数据,代入关系式求值,然后根据所求值回答其实际意义.
课堂探究
规律方法
3.已知函数模型解决实际问题
往往给出的函数解析式含有参数,
需要将题中的数据代入函数模型,求得函数模型中的参数,
再将问题转化为已知函数解析式求函数值或自变量的值.
【跟踪训练1】
我们知道,燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度(单位:m/s)可以表示为函数v=5log2,其中Q表示燕子的耗氧量.计算:
(1)当燕子静止时的耗氧量是多少个单位
(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少
课堂探究
解 (1)由题意知,当燕子静止时,它的速度v=0,
代入题中公式,可得0=5log2,解得Q=10个单位.
(2)将耗氧量Q=80代入题中公式,得v=5log2=5log28=15(m/s).
课堂探究
例2 某市“网约车”的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
(1)将某乘客搭乘一次“网约车”的费用f(x)(单位:元)表示为行程x(0
解 (1)由题意得车费f(x)关于路程x的函数为
f(x)=即f(x)=
课堂探究
例2 某市“网约车”的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85元/km).
(2)某乘客的行程为16 km,他准备先乘一辆“网约车”行驶8 km后,再换乘另一辆“网约车”完成余下行程,请问:他这样做是否比只乘一辆“网约车”完成全部行程更省钱 请说明理由.
探究四 建立适当的函数模型解决实际问题
(2)只乘一辆车的车费为f(16)=2.85×16 5.3=40.3(元),
换乘2辆车的车费为2f(8)=2×(4.2+1.9×8)=38.8(元).
因为40.3>38.8,所以该乘客换乘比只乘一辆车更省钱.
课堂探究
规律方法
1.一次函数模型的应用
利用一次函数求最值,常转化为求解不等式(或).
解答时,注意系数的正负,
也可以结合函数图象或其单调性来求最值.
课堂探究
规律方法
2.利用二次函数求最值的方法及注意点
方法:根据实际问题建立函数模型解析式后,
可利用配方法、判别式法、换元法及利用函数的单调性等方法求最值,
从而解决实际问题中的利润最大、用料最省等最值问题.
注意:取得最值时的自变量与实际意义是否相符.
课堂探究
规律方法
3.应用分段函数时的三个注意点
(1)分段函数的“段”一定要分得合理,不重不漏.
(2)分段函数的定义域为对应每一段自变量取值范围的并集.
(3)分段函数的值域求法为逐段求函数值的范围,最后比较再下结论.
【跟踪训练2】
某车间生产一种仪器的固定成本为10 000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=
其中x是仪器的月产量. (总收入=总成本+利润)
(1)将利润表示为月产量的函数(用f(x)表示);
课堂探究
解 (1)设总成本为t,则t=10 000+100x.
因为f(x)=H(x) t,
所以f(x)=
【跟踪训练2】
某车间生产一种仪器的固定成本为10 000元,每生产一台该仪器需要增加投入100元,已知总收入满足函数:H(x)=
其中x是仪器的月产量. (总收入=总成本+利润)
(2)当月产量为何值时,车间所获利润最大 最大利润为多少元
课堂探究
(2)当0≤x≤200时,f(x)= (x 150)2+12 500,
所以当x=150时,有最大值12 500;
当x>200时,f(x)=30 000 100x是减函数,f(x)<30 000 100×200<12 500.
所以当x=150时,f(x)取得最大值,最大值为12 500.
所以当每月生产150台仪器时,利润最大,最大利润为12 500元.
课堂探究
例3 某纪念章从2024年6月1日起开始上市.通过市场调查,得到该纪念章每枚的市场价y(单位:元)与上市时间x(单位:天)的数据如下:
(1)根据上表数据结合散点图,从下列函数中选取一个恰当的函数描述该纪念章的市场价y与上市时间x的变化关系并说明理由:
①y=ax+b;②y=ax2+bx+c;③y=alogbx;
(2)利用你选取的函数,求该纪念章市场价最低时的上市天数及最低的价格.
探究五 根据拟合效果选择恰当的函数模型解决实际问题
上市时间x天 4 10 36
市场价y元 90 51 90
课堂探究
解 (1)∵随着时间x的增加,y的值先减后增,而所给的三个函数中y=ax+b和y=alogbx显然都是单调函数,不满足题意,
∴用函数y=ax2+bx+c描述该纪念章的市场价y与上市时间x的变化关系.
(2)把点(4,90),(10,51),(36,90)的坐标分别代入y=ax2+bx+c中,
得解得
∴y=x2 10x+126=(x 20)2+26.
∴当x=20时,y有最小值26.
故该纪念章市场价最低时的上市天数为20天,最低的价格为26元.
课堂探究
规律方法
建立函数模型应遵循的三个原则
简化原则:建立函数模型,原型一定要简化,抓主要因素、主要变量,尽量建立较低阶、较简便的模型.
可推演原则:建立模型,一定要有意义,既能做理论分析,又能计算、推理,且能得出正确结论.
反映性原则:建立模型,应与原型具有“相似性”,所得模型的解应具有说明问题的功能,能回到具体问题中解决问题.
【跟踪训练3】
芦荟是一种经济价值很高的观赏、食用植物,不仅可美化居室、净化空气,又可美容保健,因此深受人们欢迎,在国内占有很大的市场.某人准备进军芦荟市场,栽培芦荟,为了了解行情,进行市场调研,从4月1日起,芦荟的种植成本Q(单位:元/10 kg)与上市时间t(单位:天)的数据情况如表:
(1)根据表中数据,从下列函数中选取一个最能反映芦荟种植成本Q与上市时间t的变化关系:Q=at+b,Q=at2+bt+c,Q=a·bt,Q=alogbt,并说明理由;
(2)利用你选择的函数,求芦荟种植成本最低时的上市天数及最低种植成本.
课堂探究
t 50 110 250
Q 150 108 150
课堂探究
解 (1)由所提供的数据可知,刻画芦荟种植成本Q与上市时间t的变化关系的函数不可能是常数函数,若用函数Q=at+b,Q=a·bt,Q=alogbt中的任意一个来反映时都应有a≠0,且上述三个函数均为单调函数,这与表格所提供的数据不符合,所以应选用二次函数Q=at2+bt+c进行描述.
将表格所提供的三组数据分别代入函数Q=at2+bt+c,
可得解得a=,b= ,c=.
所以,刻画芦荟种植成本Q与上市时间t的变化关系的函数Q=t2 t+.
(2)当t= =150(天)时,芦荟种植成本最低为Q=×1502 ×150+=100(元/10 kg).
评价反馈
解析 由题中图象知,在不同时段内,路程折线图不同,
故对应的函数模型为分段函数.
1. 如果一辆汽车在某段路途中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数
B.二次函数
C.指数型函数
D.对数型函数
A
评价反馈
解析 当x=1时,由3 000=alog3(1+2),得a=3 000,
所以到2026年冬,即第7年,y=3 000×log3(7+2)=6 000.故选C.
2. 据统计,每年到鄱阳湖国家湿地公园越冬的白鹤数量y(单位:只)与时间x(单位:年)近似满足关系y=alog3(x+2),观测发现2020年冬(作为第1年)有越冬白鹤3 000只,估计到2026年冬有越冬白鹤( )
A.4 000只 B.5 000只
C.6 000只 D.7 000只
C
评价反馈
解析 设甲地销售x辆,则乙地销售(15 x)辆,
从而总利润为S=(5.06x 0.15x2)+2(15 x)= 0.15x2+3.06x+30(0≤x≤15,x∈N).
显然,当x=10时,S取得最大值S=45.6. 故选B.
3. 某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x 0.15x2和L2=2x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为( )
A.45.606 B.45.6
C.45.56 D.45.51
B
评价反馈
解析 由平均增长率的定义可知,(1+x)20=4.故选D.
4. 某工厂引进先进生产技术,产品产量从2023年1月到2024年8月的20个月间翻了两番,设月平均增长率为x,则有( )
A.(1+x)19=4 B.(1+x)20=3
C.(1+x)20=2 D.(1+x)20=4
D
评价反馈
5. 某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
则下列函数模型中,能较好地反映计算机在第x天被感染的数量y与x之间的关系的是( )
A.y=10x B.y=5x2 5x+10
C.y=10log2x+10 D.y=5×2x
D
第x天 1 2 3 4 5
被感染的计算机数量y/台 10 20 39 81 160
评价反馈
解析 对于A选项,当x=1,2,3,4,5时,对应的y值分别为10,20,30,40,50;对于B选项,当x=1,2,3,4,5时,对应的y值分别为10,20,40,70,110;对于C选项,当x=1,2,3,4,5时,对应的y值分别为10,20,10+10log23,30,10+10log25;对于D选项,当x=1,2,3,4,5时,对应的y值分别为10,20,40,80,160.而表中所给的数据当x=1,2,3,4,5时,对应的y值分别为10,20,39,81,160,通过比较,即可发现选项D中y的值误差最小,即y=5×2x能较好地反映y与x之间的关系,故选D.
评价反馈
解析 将x=3分别代入y=x2+1及y=3x 1中,
得y=32+1=10,y=3×3 1=8.
因为10更接近10.2,
所以选用甲模型.
6. 现测得(x,y)的两组对应值分别为(1,2),(2,5),现有两个待选模型,
甲:y=x2+1,乙:y=3x 1,若又测得(x,y)的一组对应值为(3,10.2),
则应选用 作为函数模型.
甲
课堂小结
知识构建
课堂小结
问题思考
(1)通过这节课,你学到了什么知识
(2)在解决问题时,用到了哪些数学思想
布置作业
完成教材第154页练习第1,2题;第155页习题4.5第6,8,9题.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
