第四章 数学建模 建立函数模型解决实际问题--人教A版高中数学必修第一册教学课件(共31张PPT)
文档属性
| 名称 | 第四章 数学建模 建立函数模型解决实际问题--人教A版高中数学必修第一册教学课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:38:27 | ||
图片预览










文档简介
(共31张PPT)
数学建模 建立函数模型解决实际问题
第四章 指数函数与对数函数
数学
学习目标
①通过参与数学建模的全过程,了解数学建模的概念,掌握数学建模的基本过程.
②在探究数学建模的过程中,进一步体会函数模型在现实生活中的应用,感受数学的应用价值.
③体会课题研究的过程,感受课题研究的意义,提升数学建模核心素养.
学习重难点
重点:
将实际问题转化为数学问题,数据的收集与函数模型的选择和建立.
难点:
数据的收集,函数模型的选择.
课堂导入
复习回顾
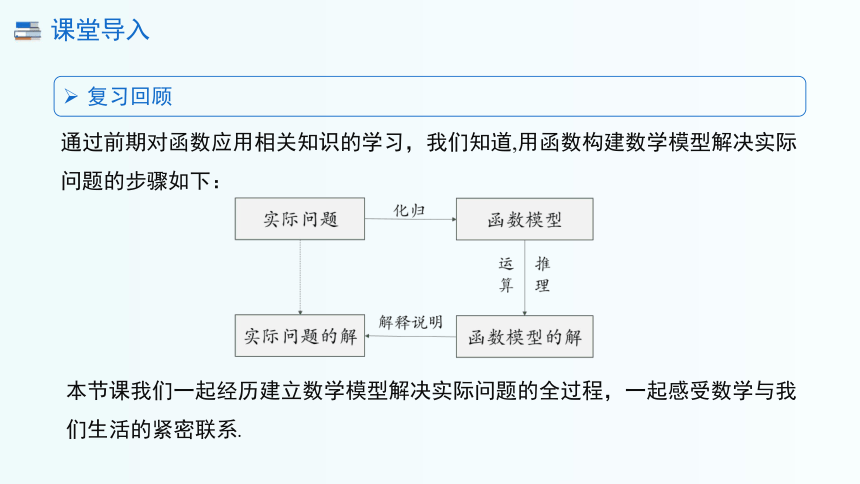
通过前期对函数应用相关知识的学习,我们知道,用函数构建数学模型解决实际问题的步骤如下:
本节课我们一起经历建立数学模型解决实际问题的全过程,一起感受数学与我们生活的紧密联系.
课堂探究
探究一 数学建模活动的一个实例
1. 实际情境
我国是茶的故乡,是世界上最早发现茶树、利用茶叶和栽培茶叶的国家,也是茶文化的发源地.中国茶道的主要内容讲究五境之美,即茶叶、茶水、火候、茶具、环境,其中茶叶可分为绿茶、红茶、乌龙茶、白茶、黄茶和黑茶.
茶文化的内涵其实就是中国文化的一种具体表现.中国素有礼仪之邦之称谓,茶文化的精神内涵即是通过沏茶、赏茶、闻茶、饮茶、品茶等习惯.
课堂探究
相关因素可能包含有茶叶类型、水温、茶具、泡茶用水、冲泡方法、茶叶用量、冲泡次数等.
2. 提出问题
思考1:影响茶水口感的因素有哪些
茶已成为全世界最大众化、最受欢迎、最有益于身心健康的绿色饮料.那你知道如何才能泡制一杯口感最佳的茶水吗
课堂探究
思考2:如何处理这些影响因素呢
将水温作为主要因素,收集水温随时间变化的数据,为了减少次要因素对结果的影响,在实验过程中
(1)选择同一种且等量的茶叶冲泡;
(2)使用同一个茶具,比如同一个玻璃杯;
(3)固定初始泡茶的水温为85 ℃;
(4)在同一环境温度25 ℃下,使用相同纯净水,并用相同的泡茶方法等.
突出主要因素,弱化次要因素
课堂探究
茶水降温的过程中也伴随着时间的变化,
因此我们可以建立茶水温度随时间变化的函数模型,将该茶水温度的实测过程转变为时间估计的问题,使得不用时刻测试水温,进而根据函数模型,通过简单计算就可以知道大约需要放置多长时间才能达到特定温度.
思考3:如何刻画茶水降温的过程
课堂探究
3. 转化问题
经验表明,某种绿茶用85 ℃的水泡制,再等到茶水温度降至60 ℃时饮用,可以产生最佳口感.那么在25 ℃室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感
课堂探究
活动1:请同学们小组合作,为获取数据设计实验流程.
用85℃的纯净水泡好一杯茶, 每隔1分钟测量一次茶水温度,并进行记录.
思考1:该实验过程需要用到哪些测量工具
秒表和温度计.
4. 收集数据
可多次重复实验,取平均值从而减小误差.
思考2:怎样保证测量数据的准确性以减少误差
课堂探究
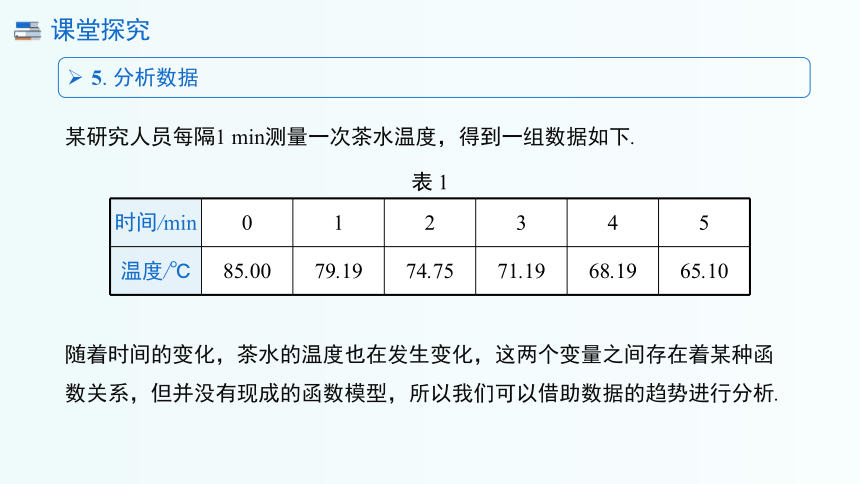
某研究人员每隔1 min测量一次茶水温度,得到一组数据如下.
5. 分析数据
随着时间的变化,茶水的温度也在发生变化,这两个变量之间存在着某种函数关系,但并没有现成的函数模型,所以我们可以借助数据的趋势进行分析.
表 1
时间/min 0 1 2 3 4 5
温度/℃ 85.00 79.19 74.75 71.19 68.19 65.10
课堂探究
设茶水温度从85 ℃开始,经过x min后的温度为y ℃,根据上表,画散点图如图所示.
思考1:观察散点图,两个变量有怎样的变化趋势
思考2:当时间不断延长,最终茶水能降到什么温度
5. 分析数据
思考3:能否找到符合趋势的函数模型
观察散点图的分布状况,并考虑到茶水温度降至室温就不能再降的事实,可选择函数y=kax+25(k∈R,0课堂探究
根据实际情况可知,当x=0时,y=85,可得k=60.
思考1:如何利用以上实验数据求解函数模型中的参数 k
得到函数模型:,
即
6. 建立模型
课堂探究
6. 建立模型
为了求出温度的衰减比例 a,可从第2 min的温度数据开始,计算每分(y 25)的值与上一分(y 25)值的比值,如表2.
x 0 1 2 3 4 5
60.00 54.19 48.75 46.19 43.19 40.10
比值 0.903 2 0.918 1 0.928 4 0.935 1 0.928 5
表 2
思考2:如何利用以上实验数据求解函数模型中的参数 a
课堂探究
结合这五个函数图象与实际数据的吻合情况,应该如何选取的值
6. 建立模型
课堂探究
比较五个函数的吻合程度,与实际数据更加吻合的是当比值为0.918 1时,
因此可以选择函数作为本题的模型.
追问:为使与每个测量点更加吻合,是不是还有更理想的值
6. 建立模型
计算各比值的平均值,得
a=×(0.903 2+0.918 1+0.928 4+0.935 1+0.928 5)=0.922 7.
我们把这个平均值作为衰减比例,就得到一个函数模型
y=60×0.922 7x+25(x≥0).
课堂探究
不难发现,采用平均值作为衰减比例与实际数据更加的吻合,
因此最终选取的函数模型为y=60×0.922 7x+25(x≥0).
7. 检验模型
将已知数据代入y=60×0.922 7x+25(x≥0),或画出函数y=60×0.922 7x+25(x≥0)的图象.
课堂探究
这种采用平均值的方法在解决实际问题中也是很常见的.因为实验所得的数据并不一定具有很强的规律性,所以我们在实验过程中应尽量重复大量实验,以保证数据的代表性,而在函数模型的选择上也是多样的,所选择的函数模型一般也只能大致反应茶水温度变化的局部规律,因此,建立模型后需要对模型进行检验.
7. 检验模型
课堂探究
思考:在25室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感
至此,我们完成整个实际问题的探究,并得到在25室温下,用85水泡制的茶大约需要放置7min,温度能够降到60达到最佳饮用口感.
将y=60代入y=60×0.922 7x+25,得60×0.922 7x+25=60,
解得x=log0.922 7.
由信息技术得x≈6.699 7.
8. 求解问题
课堂探究
思考:你体会到研究这个问题具有哪些实际价值
很多实际问题的背后,可能都隐藏着某种规律,这种规律可以用实验的方法进行探究,并用数学的方法加以刻画.
活动2:请同学们小组合作,结合以上探究过程归纳数学建模的步骤.
归纳总结
课堂探究
以上问题解决过程概括如下:
归纳总结
课堂探究
请同学们仿照上述过程开展一次建立函数模型解决实际问题的活动.
可以继续研究不同室温下泡制一杯最佳口感茶水所需的时间,
也可以从下列选题中选择一个:
1.应在炒菜之前多长时间将冰箱里的肉拿出来解冻
2.根据某一同学的身高和体重,判断该同学是否超重.
3.用微波炉或电磁炉烧一壶开水,找到最省电的功率设定方法.
4.估计阅读一本书所需要的时间.
也可以根据自己的兴趣,与老师协商后确定一个课题进行研究.
探究二 数学建模活动的选题
课堂探究
三、数学建模活动的要求
评价反馈
1. 某药品分两次降价,若平均每次降价的百分率为x,该药品的原价是m元,降价后的价格是y元,则y与x的函数关系是( )
A.y=m(1 x)2
B.y=m(1+x)2
C.y=2m(1 x)
D.y=2m(1+x)
A
评价反馈
2. 若一个等腰三角形的周长为20 cm,底边长y cm是腰长x cm的函数,则此函数的定义域是( )
A.(0,10) B.(0,5)
C.(5,10) D.[5,10)
C
解析 由题意知y=20 2x.
因为三角形两边之和大于第三边,
所以2x>y,即2x>20 2x,解得x>5.
又因为y>0,所以20 2x>0,解得x<10.故5评价反馈
3. 如图,给出了红豆的生长时间t(单位:月)与枝数y(单位:枝)的散点图.那么红豆的生长时间与枝数的关系用下列函数模型拟合最好的是( )
A.指数函数:y=2t B.对数函数:y=log2t
C.幂函数:y=t3 D.二次函数:y=2t2
A
解析 由题图知函数的图象在第一象限内增长越来越快,且图象过点(2,4),
故用指数函数y=2t来模拟比较好.
故选A.
评价反馈
4. 有一组实验数据如表所示,
则体现这些数据关系的最佳函数模型是( )
A.u=log2t B.u=2t 2
C.u= D.u=2t 2
C
解析 将数据代入验证,可知选C.
t 1.99 3.0 4.0 5.1 6.12
u 1.5 4.04 7.5 12 18.01
解析 从题中表格可以看出,随着x的增大,三个变量y1,y2,y3都是越来越大,但是增长速度不同,其中变量y1的增长速度最快,可知变量y1呈指数函数变化,故填y1.
评价反馈
5. 以下是三个变量y1,y2,y3随变量x变化的函数值表,
1
其中关于呈指数函数变化的是____________.
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
思考问题
本节课我们主要学习了哪些内容
1.要对实际问题中的变化过程进行深入分析,分析其中常量、变量及相互关系.
2.选择函数模型时要明确运动变化的基本特征,确定运动变化类型.
3.要选择适当的函数类型建立数学模型,将实际问题转化为数学问题.
4.利用函数模型的解描述实际问题的变化规律,达到解决问题的目的.
布置作业
根据自己的选题做一个课题研究,撰写研究报告.
谢谢大家
数学建模 建立函数模型解决实际问题
第四章 指数函数与对数函数
数学
学习目标
①通过参与数学建模的全过程,了解数学建模的概念,掌握数学建模的基本过程.
②在探究数学建模的过程中,进一步体会函数模型在现实生活中的应用,感受数学的应用价值.
③体会课题研究的过程,感受课题研究的意义,提升数学建模核心素养.
学习重难点
重点:
将实际问题转化为数学问题,数据的收集与函数模型的选择和建立.
难点:
数据的收集,函数模型的选择.
课堂导入
复习回顾
通过前期对函数应用相关知识的学习,我们知道,用函数构建数学模型解决实际问题的步骤如下:
本节课我们一起经历建立数学模型解决实际问题的全过程,一起感受数学与我们生活的紧密联系.
课堂探究
探究一 数学建模活动的一个实例
1. 实际情境
我国是茶的故乡,是世界上最早发现茶树、利用茶叶和栽培茶叶的国家,也是茶文化的发源地.中国茶道的主要内容讲究五境之美,即茶叶、茶水、火候、茶具、环境,其中茶叶可分为绿茶、红茶、乌龙茶、白茶、黄茶和黑茶.
茶文化的内涵其实就是中国文化的一种具体表现.中国素有礼仪之邦之称谓,茶文化的精神内涵即是通过沏茶、赏茶、闻茶、饮茶、品茶等习惯.
课堂探究
相关因素可能包含有茶叶类型、水温、茶具、泡茶用水、冲泡方法、茶叶用量、冲泡次数等.
2. 提出问题
思考1:影响茶水口感的因素有哪些
茶已成为全世界最大众化、最受欢迎、最有益于身心健康的绿色饮料.那你知道如何才能泡制一杯口感最佳的茶水吗
课堂探究
思考2:如何处理这些影响因素呢
将水温作为主要因素,收集水温随时间变化的数据,为了减少次要因素对结果的影响,在实验过程中
(1)选择同一种且等量的茶叶冲泡;
(2)使用同一个茶具,比如同一个玻璃杯;
(3)固定初始泡茶的水温为85 ℃;
(4)在同一环境温度25 ℃下,使用相同纯净水,并用相同的泡茶方法等.
突出主要因素,弱化次要因素
课堂探究
茶水降温的过程中也伴随着时间的变化,
因此我们可以建立茶水温度随时间变化的函数模型,将该茶水温度的实测过程转变为时间估计的问题,使得不用时刻测试水温,进而根据函数模型,通过简单计算就可以知道大约需要放置多长时间才能达到特定温度.
思考3:如何刻画茶水降温的过程
课堂探究
3. 转化问题
经验表明,某种绿茶用85 ℃的水泡制,再等到茶水温度降至60 ℃时饮用,可以产生最佳口感.那么在25 ℃室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感
课堂探究
活动1:请同学们小组合作,为获取数据设计实验流程.
用85℃的纯净水泡好一杯茶, 每隔1分钟测量一次茶水温度,并进行记录.
思考1:该实验过程需要用到哪些测量工具
秒表和温度计.
4. 收集数据
可多次重复实验,取平均值从而减小误差.
思考2:怎样保证测量数据的准确性以减少误差
课堂探究
某研究人员每隔1 min测量一次茶水温度,得到一组数据如下.
5. 分析数据
随着时间的变化,茶水的温度也在发生变化,这两个变量之间存在着某种函数关系,但并没有现成的函数模型,所以我们可以借助数据的趋势进行分析.
表 1
时间/min 0 1 2 3 4 5
温度/℃ 85.00 79.19 74.75 71.19 68.19 65.10
课堂探究
设茶水温度从85 ℃开始,经过x min后的温度为y ℃,根据上表,画散点图如图所示.
思考1:观察散点图,两个变量有怎样的变化趋势
思考2:当时间不断延长,最终茶水能降到什么温度
5. 分析数据
思考3:能否找到符合趋势的函数模型
观察散点图的分布状况,并考虑到茶水温度降至室温就不能再降的事实,可选择函数y=kax+25(k∈R,0
根据实际情况可知,当x=0时,y=85,可得k=60.
思考1:如何利用以上实验数据求解函数模型中的参数 k
得到函数模型:,
即
6. 建立模型
课堂探究
6. 建立模型
为了求出温度的衰减比例 a,可从第2 min的温度数据开始,计算每分(y 25)的值与上一分(y 25)值的比值,如表2.
x 0 1 2 3 4 5
60.00 54.19 48.75 46.19 43.19 40.10
比值 0.903 2 0.918 1 0.928 4 0.935 1 0.928 5
表 2
思考2:如何利用以上实验数据求解函数模型中的参数 a
课堂探究
结合这五个函数图象与实际数据的吻合情况,应该如何选取的值
6. 建立模型
课堂探究
比较五个函数的吻合程度,与实际数据更加吻合的是当比值为0.918 1时,
因此可以选择函数作为本题的模型.
追问:为使与每个测量点更加吻合,是不是还有更理想的值
6. 建立模型
计算各比值的平均值,得
a=×(0.903 2+0.918 1+0.928 4+0.935 1+0.928 5)=0.922 7.
我们把这个平均值作为衰减比例,就得到一个函数模型
y=60×0.922 7x+25(x≥0).
课堂探究
不难发现,采用平均值作为衰减比例与实际数据更加的吻合,
因此最终选取的函数模型为y=60×0.922 7x+25(x≥0).
7. 检验模型
将已知数据代入y=60×0.922 7x+25(x≥0),或画出函数y=60×0.922 7x+25(x≥0)的图象.
课堂探究
这种采用平均值的方法在解决实际问题中也是很常见的.因为实验所得的数据并不一定具有很强的规律性,所以我们在实验过程中应尽量重复大量实验,以保证数据的代表性,而在函数模型的选择上也是多样的,所选择的函数模型一般也只能大致反应茶水温度变化的局部规律,因此,建立模型后需要对模型进行检验.
7. 检验模型
课堂探究
思考:在25室温下,刚泡好的茶水大约需要放置多长时间才能达到最佳饮用口感
至此,我们完成整个实际问题的探究,并得到在25室温下,用85水泡制的茶大约需要放置7min,温度能够降到60达到最佳饮用口感.
将y=60代入y=60×0.922 7x+25,得60×0.922 7x+25=60,
解得x=log0.922 7.
由信息技术得x≈6.699 7.
8. 求解问题
课堂探究
思考:你体会到研究这个问题具有哪些实际价值
很多实际问题的背后,可能都隐藏着某种规律,这种规律可以用实验的方法进行探究,并用数学的方法加以刻画.
活动2:请同学们小组合作,结合以上探究过程归纳数学建模的步骤.
归纳总结
课堂探究
以上问题解决过程概括如下:
归纳总结
课堂探究
请同学们仿照上述过程开展一次建立函数模型解决实际问题的活动.
可以继续研究不同室温下泡制一杯最佳口感茶水所需的时间,
也可以从下列选题中选择一个:
1.应在炒菜之前多长时间将冰箱里的肉拿出来解冻
2.根据某一同学的身高和体重,判断该同学是否超重.
3.用微波炉或电磁炉烧一壶开水,找到最省电的功率设定方法.
4.估计阅读一本书所需要的时间.
也可以根据自己的兴趣,与老师协商后确定一个课题进行研究.
探究二 数学建模活动的选题
课堂探究
三、数学建模活动的要求
评价反馈
1. 某药品分两次降价,若平均每次降价的百分率为x,该药品的原价是m元,降价后的价格是y元,则y与x的函数关系是( )
A.y=m(1 x)2
B.y=m(1+x)2
C.y=2m(1 x)
D.y=2m(1+x)
A
评价反馈
2. 若一个等腰三角形的周长为20 cm,底边长y cm是腰长x cm的函数,则此函数的定义域是( )
A.(0,10) B.(0,5)
C.(5,10) D.[5,10)
C
解析 由题意知y=20 2x.
因为三角形两边之和大于第三边,
所以2x>y,即2x>20 2x,解得x>5.
又因为y>0,所以20 2x>0,解得x<10.故5
3. 如图,给出了红豆的生长时间t(单位:月)与枝数y(单位:枝)的散点图.那么红豆的生长时间与枝数的关系用下列函数模型拟合最好的是( )
A.指数函数:y=2t B.对数函数:y=log2t
C.幂函数:y=t3 D.二次函数:y=2t2
A
解析 由题图知函数的图象在第一象限内增长越来越快,且图象过点(2,4),
故用指数函数y=2t来模拟比较好.
故选A.
评价反馈
4. 有一组实验数据如表所示,
则体现这些数据关系的最佳函数模型是( )
A.u=log2t B.u=2t 2
C.u= D.u=2t 2
C
解析 将数据代入验证,可知选C.
t 1.99 3.0 4.0 5.1 6.12
u 1.5 4.04 7.5 12 18.01
解析 从题中表格可以看出,随着x的增大,三个变量y1,y2,y3都是越来越大,但是增长速度不同,其中变量y1的增长速度最快,可知变量y1呈指数函数变化,故填y1.
评价反馈
5. 以下是三个变量y1,y2,y3随变量x变化的函数值表,
1
其中关于呈指数函数变化的是____________.
x 1 2 3 4 5 6 7 8 …
y1 2 4 8 16 32 64 128 256 …
y2 1 4 9 16 25 36 49 64 …
y3 0 1 1.585 2 2.322 2.585 2.807 3 …
思考问题
本节课我们主要学习了哪些内容
1.要对实际问题中的变化过程进行深入分析,分析其中常量、变量及相互关系.
2.选择函数模型时要明确运动变化的基本特征,确定运动变化类型.
3.要选择适当的函数类型建立数学模型,将实际问题转化为数学问题.
4.利用函数模型的解描述实际问题的变化规律,达到解决问题的目的.
布置作业
根据自己的选题做一个课题研究,撰写研究报告.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
