第四章 指数函数与对数函数 本章小结--人教A版高中数学必修第一册教学课件(共56张PPT)
文档属性
| 名称 | 第四章 指数函数与对数函数 本章小结--人教A版高中数学必修第一册教学课件(共56张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 18:38:48 | ||
图片预览









文档简介
(共56张PPT)
本章小结
第四章 指数函数与对数函数
数学
学习目标
①掌握指数函数、对数函数的概念、图象和性质,并能用图象和性质解决有关问题.
②了解指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,通过对几类基本初等函数的变化差异进行比较,来解决简单的实际问题.
③掌握运用函数性质求方程近似解的基本方法(二分法);理解用函数构建数学模型的基本过程;运用模型思想发现和提出、分析和解决问题.
学习重难点
重点:
指数函数、对数函数的图象与性质及其应用,特别是单调性的应用.
难点:
与指数、对数函数有关的函数值域和复合函数的单调性问题和选择恰当
的函数模型解决实际问题.
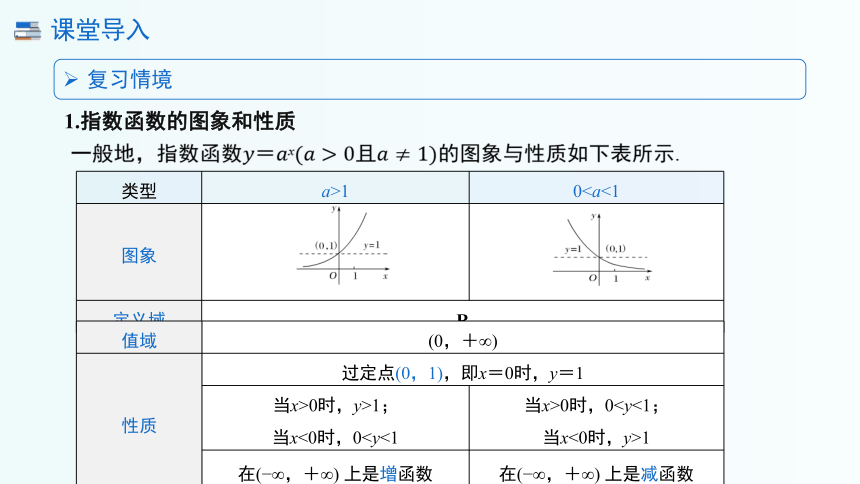
1.指数函数的图象和性质
一般地,指数函数x且的图象与性质如下表所示.
类型 a>1 0图象
定义域 R 值域 (0,+∞) 性质 过定点(0,1),即x=0时,y=1 当x>0时,y>1; 当x<0时,00时,0当x<0时,y>1
在( ∞,+∞) 上是增函数 在( ∞,+∞) 上是减函数
课堂导入
复习情境
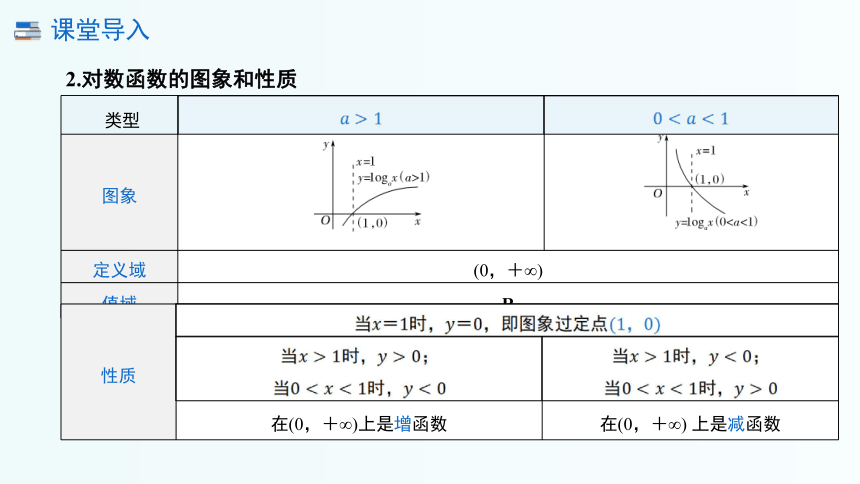
2.对数函数的图象和性质
类型
图象
定义域 (0,+∞) 值域 R 性质
在(0,+∞)上是增函数 在(0,+∞) 上是减函数
课堂导入
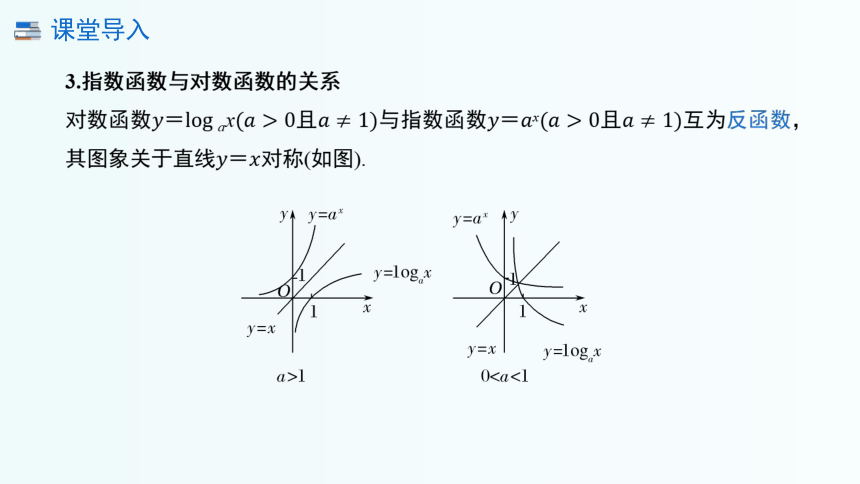
3.指数函数与对数函数的关系
对数函数ax且与指数函数x且互为反函数,其图象关于直线对称(如图).
课堂导入
4.函数的零点与方程的根的关系
函数的零点就是方程的解,
函数的零点的个数与方程的解的个数相等,
也可以说方程的解就是函数的图象与轴交点的横坐标,
即函数的函数值等于时自变量的取值.
因此方程的解的问题可以转化为函数问题来解决.
讨论方程的解所在的大致区间可以转化为讨论函数的零点所在的大致区间,
讨论方程的解的个数可以转化为讨论函数的零点的个数.
课堂导入
5.函数零点存在定理
(1)该定理的条件是:
①函数在区间上的图象是连续不断的;
②, 即和的符号相反. 这两个条件缺一不可.
(2)该定理的结论是“至少存在一个零点”,仅仅能确定函数零点是存在的,但是不能确定函数零点的个数.
课堂导入
6.函数模型的应用
(1)要解决函数应用问题,首先要增强应用函数的意识. 一般来说,解决函数应用问题可分三步:第一步,理解题意,弄清关系;第二步,抓住关键,建立模型;第三步,数学解决、检验模型.其中第二步尤为关键.
(2)在解题中要充分运用数形结合、转化与化归、函数与方程等数学思想及策略,寻求解题途径.
(3)根据已知条件建立函数解析式是函数应用的一个重要方面. 一般分为两类:一类是借助于生活经验、函数知识等建立函数模型,以二次函数模型为主,一般是求二次函数的最值. 另一类是根据几何、物理概念建立函数模型.
课堂导入
课堂导入
课前自测
1.(多选题)下列运算正确的是( )
A.=log85 B.当a>0时,
C.若a+a 1=14,则=3 D.(+ln(ln e)=7
解析 对于A选项,=log58,故A选项错误;
对于B选项,当a>0时,,故B选项正确;
对于C选项,令=m,则m2=a+a 1+2=16,故m≠3,选项C错误;
对于D选项,(+ln(ln e)=+ln 1=7,故选项D正确.故选BD.
BD
课堂导入
2.(多选题)如果函数f(x)=loga|x 1|在区间(0,1)内单调递减,那么( )
A.f(x)在(1,+∞)上单调递增且无最大值
B.f(x)在(1,+∞)上单调递减且无最小值
C.f(x)在定义域内是偶函数
D.f(x)的图象关于直线x=1对称
解析 因为函数f(x)=loga|x 1|在区间(0,1)内单调递减,所以f(x)=loga(1 x)在区间(0,1)内单调递减,而y=1 x是减函数,所以a>1,又因为y=x 1是增函数,所以f(x)在(1,+∞)上单调递增且无最大值,故选项A正确,选项B错误;函数f(x)=loga|x 1|的定义域为( ∞,1)∪(1,+∞),不关于原点对称,所以f(x)为非奇非偶函数,故选项C错误;因为f(2 x)=loga|2 x 1|=loga|x 1|=f(x),所以f(x)的图象关于直线x=1对称,故选项D正确.故选AD.
AD
课堂导入
3.若函数y=ax(a>0且a≠1)在区间[2,4]上的最大值比最小值大,则a= .
解析 若0所以f(x)max=a2,f(x)min=a4,由题意得a2 a4=,解得a=.
若a>1,则函数f(x)=ax在区间[2,4]上单调递增,
所以f(x)max=a4,f(x)min=a2,
由题意得a4 a2=,解得a=.
综上所述,a的取值为.
课堂探究
探究一 指数、对数运算
1.指数、对数的运算主要考查:
对数与指数的互化
对数、指数的运算性质
换底公式
利用运算性质进行化简、计算、证明
2.掌握基本运算性质,重点提升数学运算素养.
例1 求下列各式的值:
(1)(+10lg 2;(2)(lg 5)2+lg 2×lg 500 lg log29×log32.
解 (1)(10lg 2()3]
() 2()2.
(2)(lg 5)2+lg 2×lg 500 lg log29×log32
=(lg 5)2+lg 2×lg 5+2lg 2 lg log39
=lg 5×(lg 5+lg 2)+2lg 2 lg 2+1 2
=lg 5+lg 2 1=1 1=0.
课堂探究
课堂探究
规律方法
指数、对数的运算应遵循的原则
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.
对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式、换底公式是对数计算、化简、证明常用的技巧.
课堂探究
【变式训练1】
(1)计算:+log2(log216)= .
(2)若2x=3,log4=y,则x+2y的值为 .
3
解析 (1)原式=(+log24=+2=.
(2)由2x=3,log4=y得x=log23,y=log4log2,
所以x+2y=log23+log2=log28=3.
课堂探究
【变式训练2】
(1) (2)0.5+0.1 2+(2 3π0+=( )
A.99 B.80 C.100 D.95
C
解析 (1)原式=(+() 2+( 3+
=[()2]+() 2+[()3] 3+
+100+ 3+=100.
课堂探究
【变式训练2】
(2)计算(log64+log63) (log312 2log32)=( )
A.0 B.1 C.2 D.4
B
(2)原式=(log6+log63)(log312 log322)
=log6(2×3)·log3=1,
故选B.
课堂探究
1.指数函数、对数函数的图象及应用
一是已知函数解析式求作函数图象,即“知式求图”;
二是判断方程的根的个数时,通常不具体解方程,而是转化为判断指数函数、对数函数等函数的图象交点个数问题.
2.掌握指数函数、对数函数图象的作法以及简单的图象平移翻折变换,提升直观想象和逻辑推理素养.
探究二 指数函数、对数函数的图象及其应用
例2 (1)若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
解析 由已知函数图象可得loga3=1,所以a=3.A项中函数的解析式是y=3 x,在R上单调递减,与图象不符;C项中函数的解析式是y=( x)3= x3,当x>0时,y<0,与图象不符;D项中函数的解析式是y=log3( x),在( ∞,0)上是减函数,与图象不符;B项中函数的解析式是y=x3,与图象相符.故选B.
课堂探究
B
例2 (2)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=()x.
①在下图中画出函数f(x)的图象;
②根据图象写出f(x)的单调区间,并写出函数的值域.
(2)解 ①先作出当x≥0时,f(x)=()x的图象,利用偶函数的
图象关于y轴对称,再作出f(x)在x∈( ∞,0)时的图象.
②函数f(x)的单调递增区间是( ∞,0),单调递减区间
是[0,+∞),值域是(0,1].
课堂探究
课堂探究
规律方法
1.识别函数的图象从以下几个方面入手:
单调性:函数图象的变化趋势;
奇偶性:函数图象的对称性;
特殊点对应的函数值.
2.指数函数与对数函数图象经过定点的实质是
a0=1,loga1=0,其中a>0,且a≠1.
解析 (1)由f(4)g(4)<0,知a2·loga4<0,则loga4<0,可知0故f(x)和g(x)在(0,+∞)上都单调递减.
课堂探究
【变式训练3】
(1)已知f(x)=ax 2,g(x)=loga|x|(a>0,且a≠1),若f(4)g(4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图象是( )
B
课堂探究
【变式训练3】
(2)若函数f(x)=loga(2x+b 1)(a>0,a≠1)的图象如图所示,则a,b满足的关系
是( )
A.0C.0(2)由函数图象可知,f(x)在R上单调递增,又y=2x+b 1在R上单调递增,故a>1.
函数图象与y轴的交点坐标为(0,logab),由函数图象可知 1即logaa 1综上有0A
课堂探究
解 (1)因为f(x)为奇函数,所以f( x)= f(x),
所以lo= lo=lo,所以,
即(1+ax)(1 ax)= (x+1)(x 1),
所以a= 1(a=1舍去).
例3 设f(x)=lo为奇函数,a为常数.
(1)求a的值; (2)试说明f(x)在区间(1,+∞)上单调递增.
探究三 指数函数、对数函数的性质及其应用
课堂探究
(2)由(1)可知f(x)=lo=lo(1+)(x>1),
令u(x)=1+(x>1),
对任意的1因为10,x2 1>0,x2 x1>0,所以>0,
即u(x1) u(x2)>0. 所以函数u(x)=1+在(1,+∞)上是减函数.
又因为函数y= lou在(0,+∞)上是减函数,
所以f(x)= lo在区间(1,+∞)上单调递增.
例3 设f(x)=lo为奇函数,a为常数.
(1)求a的值; (2)试说明f(x)在区间(1,+∞)上单调递增.
课堂探究
【变式训练4】
解析 (1)由题意得解得 2所以f(x)的定义域是( 2,2),关于原点对称.
因为f( x)=ln(2 x) ln(2+x)= f(x),所以f(x)是奇函数;
又y=ln(2+x)在区间( 2,2)上单调递增,y=ln(2 x)在区间( 2,2)上单调递减,
所以f(x)在区间( 2,2)上单调递增.故选A.
(1)设函数f(x)=ln(2+x) ln(2 x),则f(x)是( )
A.奇函数,且在区间(0,2)上单调递增
B.奇函数,且在区间(0,2)上单调递减
C.偶函数,且在区间(0,2)上单调递增
D.偶函数,且在区间(0,2)上单调递减
A
课堂探究
【变式训练4】
(2)因为0所以函数y=loga (2x1)在区间[3,6]上单调递减,
所以当x=6时,y有最小值为2,即loga11=2,
所以a 211,解得a
(2)若函数y=loga (2x1)(0为 .
课堂探究
规律方法
1.确定函数的定义域,研究或利用函数的性质,都要在其定义域上进行.
2.如果需将函数解析式变形,一定要保证其等价性,否则结论错误.
3.在解决与对数函数相关的比较大小或解不等式问题时,要优先考虑利用对数函数的单调性来求解. 在利用单调性时,一定要明确底数a的取值对函数增减性的影响,及真数必须为正的限制条件.
课堂探究
规律方法
求与指数、对数函数有关的函数值域和复合函数的单调性问题,必须弄清三方面的问题:
一是定义域,所有问题都必须在定义域内讨论;
二是底数与1的大小关系;
三是复合函数的构成,即它是由哪些基本初等函数复合而成的,借助“同增异减”这一性质分析判断.
另外,解题时要注意数形结合、分类讨论、转化与化归思想的应用.
课堂探究
1.函数的零点主要考查零点个数以及零点所在区间,主要利用了转化思想,把零点问题转化成函数与x轴交点以及两函数交点问题.
2.掌握零点存在定理及转化思想,提升逻辑推理和直观想象素养.
探究四 函数的零点与方程的根
课堂探究
解析 (1)当x>0时,f(x)=3x 1有一个零点x=.
因此当x≤0时,方程ex+a=0只有一个实根,
因为ex= a,当x≤0时,ex∈(0,1],
所以 a∈(0,1],即a∈[ 1,0),
故选D.
例4 (1)已知函数f(x)=(a∈R),若函数f(x)在R上有两个零点,则a的取值范围是( )
A.( ∞, 1) B.( ∞,1) C.( 1,0) D.[ 1,0)
D
课堂探究
(2)函数g(x)=f(x)+x+a存在2个零点,
即关于x的方程f(x)= x a有2个不同的实根,
即函数f(x)的图象与直线y= x a有2个交点.
作出直线y= x a与函数f(x)的图象,
如图所示,由图可知 a≤1,解得a≥ 1,故选C.
例4 (2)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[ 1,0) B.[0,+∞) C.[ 1,+∞) D.[1,+∞)
C
课堂探究
规律方法
1.已知函数的零点求参数,主要方法有:
(1)直接求方程的根,构建方程(不等式)求参数;
(2)数形结合;
(3)分离参数,转化为求函数的最值.
2.已知函数零点的个数求参数范围,常利用数形结合法将其转化为两个函数的图象的交点个数问题,需准确画出两个函数的图象,利用图象写出满足条件的参数范围.
课堂探究
【变式训练5】
解析 (1)若λ=2,当x≥2时,令x 4<0,得2≤x<4;
当x<2时,令x2 4x+3<0,解得1综上可知,1(2)令f(x)=0,当x≥λ时,x=4,
当x<λ时,x2 4x+3=0,解得x=1或x=3.
因为函数f(x)恰有2个零点,
如图,结合函数的图象知1<λ≤3或λ>4.
(1,4)
已知λ∈R,函数f(x)=
(1)当λ=2时,不等式f(x)<0的解集是 .
(2)若函数f(x)恰有2个零点,则λ的取值范围是 .
(1,3]∪(4,)
课堂探究
建立恰当的函数模型解决实际问题的步骤:
(1)对实际问题进行抽象概括,确定变量之间的关系,并分别用x,y表示.
(2)建立函数模型,将变量y表示为x的函数,此时要注意函数的定义域.
(3)求解函数模型,并还原为实际问题的解.
探究五 函数模型的应用
课堂探究
例5 “活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:
“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.
当x不超过4尾/立方米时,v的值为2千克/年;
当4当x达到20尾/立方米时,因缺氧等原因,v的值为0千克/年.
(1)当0(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大 并求出最大值.
课堂探究
解 (1)由题意得当0显然v=ax+b在(4,20]内是减函数.由已知得
解得所以v= x+.故函数v=
(2)设年生长量为f(x)千克/立方米.
根据题意和(1)可得f(x)=
当0当4所以当0故当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,
最大值为12.5千克/立方米.
课堂探究
规律方法
1.指数函数、对数函数模型解题,关键是对模型的判断,先设定模型,将有关数据代入验证,确定参数,求解时要准确进行运算,灵活进行指数与对数的互化.
2.实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,如出租车计价与路程之间的关系,应构建分段函数模型求解.但应关注以下两点:
(1)分段要简洁合理,不重不漏;
(2)分段函数的最值是各段的最大(或最小)值中的最大(或最小)值.
课堂探究
【变式训练6】
解析 (1)设该职工用水x m3时,缴纳的水费为y元.
由题意得y=
则10m+(x 10)·2m=16m,解得x=13.
(1)某单位为鼓励职工节约用水,作出以下规定:每位职工每月用水不超过10 m3的,按每立方米m元收费;用水超过10 m3的,超过部分加倍收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A.13 m3 B.14 m3 C.18 m3 D.26 m3
A
课堂探究
【变式训练6】
(2)M≈3361,N≈1080,,
则lg≈lg=lg 3361 lg 1080=361lg 3 80≈93.
故≈1093.
(2)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg 3≈0.48)( )
A.1033 B.1053 C.1073 D.1093
D
课堂探究
规律方法
针对一个实际问题,我们应该选择恰当的函数模型来刻画.
这当然需要我们深刻理解已学函数的图象和性质,熟练掌握已学函数的特点,并对一些重要的函数模型要有清晰的认识.
对于一个具体的应用题,原题中的数量间的关系,一般是以文字和符号的形式给出,也有的是以图象的形式给出,此时我们要分析数量变化的特点和规律,选择较为接近的函数模型进行模拟,从而解决一些实际问题或预测一些结果.
1. 函数f(x)= log2(4 x2)的定义域是( )
A.( 2,0)∪(1,2)
B.( 2,0]∪(1,2)
C.( 2,0)∪[1,2)
D.[ 2,0]∪[1,2]
评价反馈
C
解析 由已知,需满足
解得x∈( 2,0)∪[1,2),
故选C.
评价反馈
解析 函数满足f( x)=f(x),是偶函数,画出函数图象如图所示,
所以函数的值域是( 1,0],故选D.
2. 函数f(x)=()|x| 1的值域是( )
A.[1,+∞) B.[0,+∞) C.( ∞,0] D.( 1,0]
D
评价反馈
解析 因为函数y=ax在区间[0,1]上是单调函数,
所以最大值与最小值都在端点处取到,
故有a0+a1=3,解得a=2,
因此函数y=2ax 1,
即y=4x 1在区间[0,1]上单调递增,ymax=4×1 1=3,故选C.
3. 若函数y=ax(a>0且a≠1)在区间[0,1]上的最大值与最小值的和为3,则函数y=2ax 1在区间[0,1]上的最大值是( )
A.6 B.1 C.3 D.
C
评价反馈
解析 由已知得loga9=2,
解得a=3,于是f(x)=log3x,
所以f(x)的反函数是g(x)=3x,
故选D.
4. 若对数函数f(x)=logax(a>0且a≠1),且图象过点(9,2),f(x)的反函数记为y=g(x),则g(x)的解析式是( )
A.g(x)=4x B.g(x)=2x
C.g(x)=9x D.g(x)=3x
D
评价反馈
解析 a=log32=,b=ln 2=,1即<1,c=,
所以c故选C.
5. 设a=log32,b=ln 2,c=,则( )
A.aC.cC
评价反馈
解析 当x≤0时,由f(x)=x+1=0,得x= 1;
当x>0时,由f(x)=log2x=0,得x=1.
所以函数f(x)的所有零点构成的集合为{ 1,1},
故选C.
6. 函数f(x)=的所有零点构成的集合为 ( )
A.{1} B.{ 1}
C.{ 1,1} D.{ 1,0,1}
C
评价反馈
解析 令g(x)=x2 ax+3a,又0<<1,则f(x)=log(x)与g(x)的增减性相反,
所以只需g(x)在区间[2,+∞)上单调递增,且g(x)>0,
所以解得 4故选B.
7. 若函数f(x)=lo(x2 ax+3a)在区间[2,+∞)上单调递减,则实数a的取值范围是( )
A.( ∞,4] B.( 4,4]
C.(0,12) D.(0,4]
B
评价反馈
解析 作出函数f(x)的图象如图,
可知f()=f(2)=1,f(1)=0,
由题意结合图象知1≤m≤2.
8. 若函数f(x)=|lox|的定义域是[,m],值域是[0,1],则m的取值范围是 .
[1,2]
评价反馈
解析 令y=a|x| |logax|=0,即a|x|=|logax|,
作出函数y=a|x|与y=|logax|在0如图,易知有两个交点,
从而函数y=a|x| |logax|的零点的个数是2.
9. 若02
评价反馈
10. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为64 ppm(ppm为浓度单位,1 ppm表示百万分之一),再过4分钟又测得浓度为32 ppm.经检验知,该地下车库一氧化碳浓度y(单位:ppm)与排气时间t(单位:分钟)之间存在函数关系y=c()mt(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟才能使这个地下车库中一氧化碳含量达到正常状态
评价反馈
解 (1)由题意可得
c()4m=64,①
c()8m=32,②
解得
所以c,m的值分别为128,.
(2)由(1)知y=128×,
令128×,
即≤()8,解得t≥32.
故至少排气32分钟才能使这个地下车库中一氧化碳含量达到正常状态.
课堂小结
知识构建
布置作业
总结反思这一章的知识和思想方法.
完成教材第159~161页复习参考题4.
谢谢大家
本章小结
第四章 指数函数与对数函数
数学
学习目标
①掌握指数函数、对数函数的概念、图象和性质,并能用图象和性质解决有关问题.
②了解指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,通过对几类基本初等函数的变化差异进行比较,来解决简单的实际问题.
③掌握运用函数性质求方程近似解的基本方法(二分法);理解用函数构建数学模型的基本过程;运用模型思想发现和提出、分析和解决问题.
学习重难点
重点:
指数函数、对数函数的图象与性质及其应用,特别是单调性的应用.
难点:
与指数、对数函数有关的函数值域和复合函数的单调性问题和选择恰当
的函数模型解决实际问题.
1.指数函数的图象和性质
一般地,指数函数x且的图象与性质如下表所示.
类型 a>1 0
定义域 R 值域 (0,+∞) 性质 过定点(0,1),即x=0时,y=1 当x>0时,y>1; 当x<0时,0
在( ∞,+∞) 上是增函数 在( ∞,+∞) 上是减函数
课堂导入
复习情境
2.对数函数的图象和性质
类型
图象
定义域 (0,+∞) 值域 R 性质
在(0,+∞)上是增函数 在(0,+∞) 上是减函数
课堂导入
3.指数函数与对数函数的关系
对数函数ax且与指数函数x且互为反函数,其图象关于直线对称(如图).
课堂导入
4.函数的零点与方程的根的关系
函数的零点就是方程的解,
函数的零点的个数与方程的解的个数相等,
也可以说方程的解就是函数的图象与轴交点的横坐标,
即函数的函数值等于时自变量的取值.
因此方程的解的问题可以转化为函数问题来解决.
讨论方程的解所在的大致区间可以转化为讨论函数的零点所在的大致区间,
讨论方程的解的个数可以转化为讨论函数的零点的个数.
课堂导入
5.函数零点存在定理
(1)该定理的条件是:
①函数在区间上的图象是连续不断的;
②, 即和的符号相反. 这两个条件缺一不可.
(2)该定理的结论是“至少存在一个零点”,仅仅能确定函数零点是存在的,但是不能确定函数零点的个数.
课堂导入
6.函数模型的应用
(1)要解决函数应用问题,首先要增强应用函数的意识. 一般来说,解决函数应用问题可分三步:第一步,理解题意,弄清关系;第二步,抓住关键,建立模型;第三步,数学解决、检验模型.其中第二步尤为关键.
(2)在解题中要充分运用数形结合、转化与化归、函数与方程等数学思想及策略,寻求解题途径.
(3)根据已知条件建立函数解析式是函数应用的一个重要方面. 一般分为两类:一类是借助于生活经验、函数知识等建立函数模型,以二次函数模型为主,一般是求二次函数的最值. 另一类是根据几何、物理概念建立函数模型.
课堂导入
课堂导入
课前自测
1.(多选题)下列运算正确的是( )
A.=log85 B.当a>0时,
C.若a+a 1=14,则=3 D.(+ln(ln e)=7
解析 对于A选项,=log58,故A选项错误;
对于B选项,当a>0时,,故B选项正确;
对于C选项,令=m,则m2=a+a 1+2=16,故m≠3,选项C错误;
对于D选项,(+ln(ln e)=+ln 1=7,故选项D正确.故选BD.
BD
课堂导入
2.(多选题)如果函数f(x)=loga|x 1|在区间(0,1)内单调递减,那么( )
A.f(x)在(1,+∞)上单调递增且无最大值
B.f(x)在(1,+∞)上单调递减且无最小值
C.f(x)在定义域内是偶函数
D.f(x)的图象关于直线x=1对称
解析 因为函数f(x)=loga|x 1|在区间(0,1)内单调递减,所以f(x)=loga(1 x)在区间(0,1)内单调递减,而y=1 x是减函数,所以a>1,又因为y=x 1是增函数,所以f(x)在(1,+∞)上单调递增且无最大值,故选项A正确,选项B错误;函数f(x)=loga|x 1|的定义域为( ∞,1)∪(1,+∞),不关于原点对称,所以f(x)为非奇非偶函数,故选项C错误;因为f(2 x)=loga|2 x 1|=loga|x 1|=f(x),所以f(x)的图象关于直线x=1对称,故选项D正确.故选AD.
AD
课堂导入
3.若函数y=ax(a>0且a≠1)在区间[2,4]上的最大值比最小值大,则a= .
解析 若0
若a>1,则函数f(x)=ax在区间[2,4]上单调递增,
所以f(x)max=a4,f(x)min=a2,
由题意得a4 a2=,解得a=.
综上所述,a的取值为.
课堂探究
探究一 指数、对数运算
1.指数、对数的运算主要考查:
对数与指数的互化
对数、指数的运算性质
换底公式
利用运算性质进行化简、计算、证明
2.掌握基本运算性质,重点提升数学运算素养.
例1 求下列各式的值:
(1)(+10lg 2;(2)(lg 5)2+lg 2×lg 500 lg log29×log32.
解 (1)(10lg 2()3]
() 2()2.
(2)(lg 5)2+lg 2×lg 500 lg log29×log32
=(lg 5)2+lg 2×lg 5+2lg 2 lg log39
=lg 5×(lg 5+lg 2)+2lg 2 lg 2+1 2
=lg 5+lg 2 1=1 1=0.
课堂探究
课堂探究
规律方法
指数、对数的运算应遵循的原则
指数式的运算首先注意化简顺序,一般负指数先转化成正指数,根式化为分数指数幂运算,其次若出现分式则要注意分子、分母因式分解以达到约分的目的.
对数运算首先注意公式应用过程中范围的变化,前后要等价,熟练地运用对数的三个运算性质并结合对数恒等式、换底公式是对数计算、化简、证明常用的技巧.
课堂探究
【变式训练1】
(1)计算:+log2(log216)= .
(2)若2x=3,log4=y,则x+2y的值为 .
3
解析 (1)原式=(+log24=+2=.
(2)由2x=3,log4=y得x=log23,y=log4log2,
所以x+2y=log23+log2=log28=3.
课堂探究
【变式训练2】
(1) (2)0.5+0.1 2+(2 3π0+=( )
A.99 B.80 C.100 D.95
C
解析 (1)原式=(+() 2+( 3+
=[()2]+() 2+[()3] 3+
+100+ 3+=100.
课堂探究
【变式训练2】
(2)计算(log64+log63) (log312 2log32)=( )
A.0 B.1 C.2 D.4
B
(2)原式=(log6+log63)(log312 log322)
=log6(2×3)·log3=1,
故选B.
课堂探究
1.指数函数、对数函数的图象及应用
一是已知函数解析式求作函数图象,即“知式求图”;
二是判断方程的根的个数时,通常不具体解方程,而是转化为判断指数函数、对数函数等函数的图象交点个数问题.
2.掌握指数函数、对数函数图象的作法以及简单的图象平移翻折变换,提升直观想象和逻辑推理素养.
探究二 指数函数、对数函数的图象及其应用
例2 (1)若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
解析 由已知函数图象可得loga3=1,所以a=3.A项中函数的解析式是y=3 x,在R上单调递减,与图象不符;C项中函数的解析式是y=( x)3= x3,当x>0时,y<0,与图象不符;D项中函数的解析式是y=log3( x),在( ∞,0)上是减函数,与图象不符;B项中函数的解析式是y=x3,与图象相符.故选B.
课堂探究
B
例2 (2)已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=()x.
①在下图中画出函数f(x)的图象;
②根据图象写出f(x)的单调区间,并写出函数的值域.
(2)解 ①先作出当x≥0时,f(x)=()x的图象,利用偶函数的
图象关于y轴对称,再作出f(x)在x∈( ∞,0)时的图象.
②函数f(x)的单调递增区间是( ∞,0),单调递减区间
是[0,+∞),值域是(0,1].
课堂探究
课堂探究
规律方法
1.识别函数的图象从以下几个方面入手:
单调性:函数图象的变化趋势;
奇偶性:函数图象的对称性;
特殊点对应的函数值.
2.指数函数与对数函数图象经过定点的实质是
a0=1,loga1=0,其中a>0,且a≠1.
解析 (1)由f(4)g(4)<0,知a2·loga4<0,则loga4<0,可知0
课堂探究
【变式训练3】
(1)已知f(x)=ax 2,g(x)=loga|x|(a>0,且a≠1),若f(4)g(4)<0,则y=f(x),y=g(x)在同一平面直角坐标系内的大致图象是( )
B
课堂探究
【变式训练3】
(2)若函数f(x)=loga(2x+b 1)(a>0,a≠1)的图象如图所示,则a,b满足的关系
是( )
A.0C.0(2)由函数图象可知,f(x)在R上单调递增,又y=2x+b 1在R上单调递增,故a>1.
函数图象与y轴的交点坐标为(0,logab),由函数图象可知 1
课堂探究
解 (1)因为f(x)为奇函数,所以f( x)= f(x),
所以lo= lo=lo,所以,
即(1+ax)(1 ax)= (x+1)(x 1),
所以a= 1(a=1舍去).
例3 设f(x)=lo为奇函数,a为常数.
(1)求a的值; (2)试说明f(x)在区间(1,+∞)上单调递增.
探究三 指数函数、对数函数的性质及其应用
课堂探究
(2)由(1)可知f(x)=lo=lo(1+)(x>1),
令u(x)=1+(x>1),
对任意的1
即u(x1) u(x2)>0. 所以函数u(x)=1+在(1,+∞)上是减函数.
又因为函数y= lou在(0,+∞)上是减函数,
所以f(x)= lo在区间(1,+∞)上单调递增.
例3 设f(x)=lo为奇函数,a为常数.
(1)求a的值; (2)试说明f(x)在区间(1,+∞)上单调递增.
课堂探究
【变式训练4】
解析 (1)由题意得解得 2
因为f( x)=ln(2 x) ln(2+x)= f(x),所以f(x)是奇函数;
又y=ln(2+x)在区间( 2,2)上单调递增,y=ln(2 x)在区间( 2,2)上单调递减,
所以f(x)在区间( 2,2)上单调递增.故选A.
(1)设函数f(x)=ln(2+x) ln(2 x),则f(x)是( )
A.奇函数,且在区间(0,2)上单调递增
B.奇函数,且在区间(0,2)上单调递减
C.偶函数,且在区间(0,2)上单调递增
D.偶函数,且在区间(0,2)上单调递减
A
课堂探究
【变式训练4】
(2)因为0
所以当x=6时,y有最小值为2,即loga11=2,
所以a 211,解得a
(2)若函数y=loga (2x1)(0
课堂探究
规律方法
1.确定函数的定义域,研究或利用函数的性质,都要在其定义域上进行.
2.如果需将函数解析式变形,一定要保证其等价性,否则结论错误.
3.在解决与对数函数相关的比较大小或解不等式问题时,要优先考虑利用对数函数的单调性来求解. 在利用单调性时,一定要明确底数a的取值对函数增减性的影响,及真数必须为正的限制条件.
课堂探究
规律方法
求与指数、对数函数有关的函数值域和复合函数的单调性问题,必须弄清三方面的问题:
一是定义域,所有问题都必须在定义域内讨论;
二是底数与1的大小关系;
三是复合函数的构成,即它是由哪些基本初等函数复合而成的,借助“同增异减”这一性质分析判断.
另外,解题时要注意数形结合、分类讨论、转化与化归思想的应用.
课堂探究
1.函数的零点主要考查零点个数以及零点所在区间,主要利用了转化思想,把零点问题转化成函数与x轴交点以及两函数交点问题.
2.掌握零点存在定理及转化思想,提升逻辑推理和直观想象素养.
探究四 函数的零点与方程的根
课堂探究
解析 (1)当x>0时,f(x)=3x 1有一个零点x=.
因此当x≤0时,方程ex+a=0只有一个实根,
因为ex= a,当x≤0时,ex∈(0,1],
所以 a∈(0,1],即a∈[ 1,0),
故选D.
例4 (1)已知函数f(x)=(a∈R),若函数f(x)在R上有两个零点,则a的取值范围是( )
A.( ∞, 1) B.( ∞,1) C.( 1,0) D.[ 1,0)
D
课堂探究
(2)函数g(x)=f(x)+x+a存在2个零点,
即关于x的方程f(x)= x a有2个不同的实根,
即函数f(x)的图象与直线y= x a有2个交点.
作出直线y= x a与函数f(x)的图象,
如图所示,由图可知 a≤1,解得a≥ 1,故选C.
例4 (2)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[ 1,0) B.[0,+∞) C.[ 1,+∞) D.[1,+∞)
C
课堂探究
规律方法
1.已知函数的零点求参数,主要方法有:
(1)直接求方程的根,构建方程(不等式)求参数;
(2)数形结合;
(3)分离参数,转化为求函数的最值.
2.已知函数零点的个数求参数范围,常利用数形结合法将其转化为两个函数的图象的交点个数问题,需准确画出两个函数的图象,利用图象写出满足条件的参数范围.
课堂探究
【变式训练5】
解析 (1)若λ=2,当x≥2时,令x 4<0,得2≤x<4;
当x<2时,令x2 4x+3<0,解得1
当x<λ时,x2 4x+3=0,解得x=1或x=3.
因为函数f(x)恰有2个零点,
如图,结合函数的图象知1<λ≤3或λ>4.
(1,4)
已知λ∈R,函数f(x)=
(1)当λ=2时,不等式f(x)<0的解集是 .
(2)若函数f(x)恰有2个零点,则λ的取值范围是 .
(1,3]∪(4,)
课堂探究
建立恰当的函数模型解决实际问题的步骤:
(1)对实际问题进行抽象概括,确定变量之间的关系,并分别用x,y表示.
(2)建立函数模型,将变量y表示为x的函数,此时要注意函数的定义域.
(3)求解函数模型,并还原为实际问题的解.
探究五 函数模型的应用
课堂探究
例5 “活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:
“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.
当x不超过4尾/立方米时,v的值为2千克/年;
当4
(1)当0
课堂探究
解 (1)由题意得当0
解得所以v= x+.故函数v=
(2)设年生长量为f(x)千克/立方米.
根据题意和(1)可得f(x)=
当0
最大值为12.5千克/立方米.
课堂探究
规律方法
1.指数函数、对数函数模型解题,关键是对模型的判断,先设定模型,将有关数据代入验证,确定参数,求解时要准确进行运算,灵活进行指数与对数的互化.
2.实际问题中有些变量间的关系不能用同一个关系式给出,而是由几个不同的关系式构成,如出租车计价与路程之间的关系,应构建分段函数模型求解.但应关注以下两点:
(1)分段要简洁合理,不重不漏;
(2)分段函数的最值是各段的最大(或最小)值中的最大(或最小)值.
课堂探究
【变式训练6】
解析 (1)设该职工用水x m3时,缴纳的水费为y元.
由题意得y=
则10m+(x 10)·2m=16m,解得x=13.
(1)某单位为鼓励职工节约用水,作出以下规定:每位职工每月用水不超过10 m3的,按每立方米m元收费;用水超过10 m3的,超过部分加倍收费.某职工某月缴水费16m元,则该职工这个月实际用水为( )
A.13 m3 B.14 m3 C.18 m3 D.26 m3
A
课堂探究
【变式训练6】
(2)M≈3361,N≈1080,,
则lg≈lg=lg 3361 lg 1080=361lg 3 80≈93.
故≈1093.
(2)根据有关资料,围棋状态空间复杂度的上限M约为3361,而可观测宇宙中普通物质的原子总数N约为1080.则下列各数中与最接近的是(参考数据:lg 3≈0.48)( )
A.1033 B.1053 C.1073 D.1093
D
课堂探究
规律方法
针对一个实际问题,我们应该选择恰当的函数模型来刻画.
这当然需要我们深刻理解已学函数的图象和性质,熟练掌握已学函数的特点,并对一些重要的函数模型要有清晰的认识.
对于一个具体的应用题,原题中的数量间的关系,一般是以文字和符号的形式给出,也有的是以图象的形式给出,此时我们要分析数量变化的特点和规律,选择较为接近的函数模型进行模拟,从而解决一些实际问题或预测一些结果.
1. 函数f(x)= log2(4 x2)的定义域是( )
A.( 2,0)∪(1,2)
B.( 2,0]∪(1,2)
C.( 2,0)∪[1,2)
D.[ 2,0]∪[1,2]
评价反馈
C
解析 由已知,需满足
解得x∈( 2,0)∪[1,2),
故选C.
评价反馈
解析 函数满足f( x)=f(x),是偶函数,画出函数图象如图所示,
所以函数的值域是( 1,0],故选D.
2. 函数f(x)=()|x| 1的值域是( )
A.[1,+∞) B.[0,+∞) C.( ∞,0] D.( 1,0]
D
评价反馈
解析 因为函数y=ax在区间[0,1]上是单调函数,
所以最大值与最小值都在端点处取到,
故有a0+a1=3,解得a=2,
因此函数y=2ax 1,
即y=4x 1在区间[0,1]上单调递增,ymax=4×1 1=3,故选C.
3. 若函数y=ax(a>0且a≠1)在区间[0,1]上的最大值与最小值的和为3,则函数y=2ax 1在区间[0,1]上的最大值是( )
A.6 B.1 C.3 D.
C
评价反馈
解析 由已知得loga9=2,
解得a=3,于是f(x)=log3x,
所以f(x)的反函数是g(x)=3x,
故选D.
4. 若对数函数f(x)=logax(a>0且a≠1),且图象过点(9,2),f(x)的反函数记为y=g(x),则g(x)的解析式是( )
A.g(x)=4x B.g(x)=2x
C.g(x)=9x D.g(x)=3x
D
评价反馈
解析 a=log32=,b=ln 2=,1
所以c
5. 设a=log32,b=ln 2,c=,则( )
A.a
评价反馈
解析 当x≤0时,由f(x)=x+1=0,得x= 1;
当x>0时,由f(x)=log2x=0,得x=1.
所以函数f(x)的所有零点构成的集合为{ 1,1},
故选C.
6. 函数f(x)=的所有零点构成的集合为 ( )
A.{1} B.{ 1}
C.{ 1,1} D.{ 1,0,1}
C
评价反馈
解析 令g(x)=x2 ax+3a,又0<<1,则f(x)=log(x)与g(x)的增减性相反,
所以只需g(x)在区间[2,+∞)上单调递增,且g(x)>0,
所以解得 4
7. 若函数f(x)=lo(x2 ax+3a)在区间[2,+∞)上单调递减,则实数a的取值范围是( )
A.( ∞,4] B.( 4,4]
C.(0,12) D.(0,4]
B
评价反馈
解析 作出函数f(x)的图象如图,
可知f()=f(2)=1,f(1)=0,
由题意结合图象知1≤m≤2.
8. 若函数f(x)=|lox|的定义域是[,m],值域是[0,1],则m的取值范围是 .
[1,2]
评价反馈
解析 令y=a|x| |logax|=0,即a|x|=|logax|,
作出函数y=a|x|与y=|logax|在0
从而函数y=a|x| |logax|的零点的个数是2.
9. 若0
评价反馈
10. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为64 ppm(ppm为浓度单位,1 ppm表示百万分之一),再过4分钟又测得浓度为32 ppm.经检验知,该地下车库一氧化碳浓度y(单位:ppm)与排气时间t(单位:分钟)之间存在函数关系y=c()mt(c,m为常数).
(1)求c,m的值;
(2)若空气中一氧化碳浓度不高于0.5 ppm为正常,问至少排气多少分钟才能使这个地下车库中一氧化碳含量达到正常状态
评价反馈
解 (1)由题意可得
c()4m=64,①
c()8m=32,②
解得
所以c,m的值分别为128,.
(2)由(1)知y=128×,
令128×,
即≤()8,解得t≥32.
故至少排气32分钟才能使这个地下车库中一氧化碳含量达到正常状态.
课堂小结
知识构建
布置作业
总结反思这一章的知识和思想方法.
完成教材第159~161页复习参考题4.
谢谢大家
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
