苏教版小学五年级上册第七单元解决问题的策略同步练习
文档属性
| 名称 | 苏教版小学五年级上册第七单元解决问题的策略同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 89.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-03 00:00:00 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
苏教版数学五年级上册第七单元解决问题的策略同步练习
一、选择题
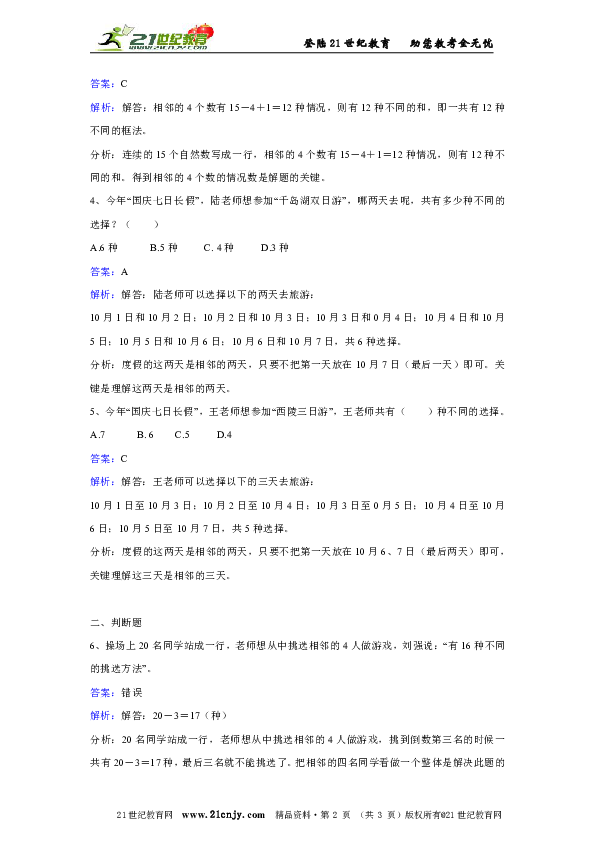
1、如图,五个正方形重叠,连结点正好是正方形的中点,正方形的边长都是a,如图的周长是 ( )。
A.24a B.18a C. 14a D.12a
答案:D
解析:解答:3a+3a+2a×3=12a
所以,这个图形的周长是12a。
分析:这五个正方形重叠在一起,第一个和最后一个正方形的长度为3a+3a,中间3个正方形的长度是2a×3=6a,把这些长度加起来就是这个图形的周长。掌握图形周长的计算方法。
2、在下面的数表中,每次框出2个数,一共有( )种不同的和。
A. 12 B. 11 C.10
答案:B
解析:解答:数字数:13-2+1=12(个)
不同的和数:12-2+1=11(个)
所以,一共有11种不同的和。
分析:从2到13递增的一行自然数,共有13-2+1=12个数字,每次框出的两个数的和不同,每向右移动一个数字就框出一个和,直到12、13为止,有12-2+1=11个不同的和。掌握数字图片的个数-框的个数+1=不同和的个数。
3、有15个连续的自然数,每次用长方形框出4个连续的自然数,一共有( )种不同的框法。
A.10 B.11 C. 12
答案:C
解析:解答:相邻的4个数有15-4+1=12种情况,则有12种不同的和,即一共有12种不同的框法。
分析:连续的15个自然数写成一行,相邻的4个数有15-4+1=12种情况,则有12种不同的和。得到相邻的4个数的情况数是解题的关键。
4、今年“国庆七日长假”,陆老师想参加“千岛湖双日游”,哪两天去呢,共有多少种不同的选择?( )
A.6种 B.5种 C. 4种 D.3种
答案:A
解析:解答:陆老师可以选择以下的两天去旅游:
10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日,共6种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月7日(最后一天)即可。关键是理解这两天是相邻的两天。
5、今年“国庆七日长假”,王老师想参加“西陵三日游”,王老师共有( )种不同的选择。
A.7 B. 6 C.5 D.4
答案:C
解析:解答:王老师可以选择以下的三天去旅游:
10月1日至10月3日;10月2日至10月4日;10月3日至0月5日;10月4日至10月6日;10月5日至10月7日,共5种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月6、7日(最后两天)即可,关键理解这三天是相邻的三天。
二、判断题
6、操场上20名同学站成一行,老师想从中挑选相邻的4人做游戏,刘强说:“有16种不同的挑选方法”。
答案:错误
解析:解答:20-3=17(种)
分析:20名同学站成一行,老师想从中挑选相邻的4人做游戏,挑到倒数第三名的时候一共有20-3=17种,最后三名就不能挑选了。把相邻的四名同学看做一个整体是解决此题的关键。
7、一个简单图形经过平移、旋转或轴对称,能形成一个较复杂的图形。
答案:正确
解析:解答:一个简单图形经过平移、旋转或轴对称,能形成一个较复杂的图形。
分析:根据图形平移、旋转、轴对称的特征,可以将一个简单的图案,通过这些变化,形成一个较复杂的图形。如,可以将一个图案通过平移形成壁报的花边、将一个梅花瓣通过四次旋转形成一朵梅花。
8、计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再进行计算。
答案:正确
解析:解答:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再根据简单图形的计算公式进行计算。
分析:根据组合图形的面积的计算方法可知:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再利用规则图形的面积公式进行计算,关键是把组合图形的面积转化为我们学过的图形的面积,再利用相应的面积公式与基本的数量关系解决问题。
9、有一列图形:○○△□□○○△□□○○△□□…,根据规律,第71个图形是○。
答案:正确
解析:解答:71÷5=14…1;余数是1,那么第71个图形就与第一个相同是○。
分析:把○○△□□看成一组,在一组中前两个图形是○,第三个是△,第四个和第五个是□,共5个;先求出71里面有几组,还余几,再根据余数判断。把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
10、下面一排圆圈共有15个,如果要给相邻的5个涂上红色.一共有11种不同的涂法。
答案:正确
解析:解答:15-5+1=11(种);
所以一共有11种不同的涂法。
分析:把相邻的5个○看作一组,每次覆盖5个,从第一个开始向右平移,每平移一次就可给相邻的5个涂上颜色,到第11个结束;所以共有11种不同的图法。掌握图形覆盖的规律是关键。
三、填空题
11、在如图中,每次框出连续4个自然数,共可得到 个不同的和。
答案:36
解析:解答:40-2+1-3
=39-3
=36
所以,可得到36个不同的和。
分析:一共有40-2+1=39个数,框出就是选连续的,如果按顺序框选,4个连续数中最小的数可以分别是2,3…,37,所以37-2+1=36,一共有36个不同的和。关键是按照顺序依次计数,做到不重复不遗漏。
12、今年“国庆七日长假”,明明想参加“西湖两日游”,哪两日去呢,他共有 种不同的选择。
答案:6
解析:解答:明明可以选择以下的两天去旅游: 10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日;共6种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月7日(最后一天)即可。关键是理解这两天是相邻的两天。
13、在下表中每次框出2个相邻的数,一共可以得到 个不同的和;如果每次框出3个相邻的数,一共可以得到 个不同的和。
答案:9|8
解析:解答:如果每次框出2个数,可以得到1+2=3;2+3=5;3+4=7;4+5=9;5+6=11;6+7=13;7+8=15;8+9=17;9+10=19;共有9个不同的和;
每次框出3个数,可以得到1+2+3=6;2+3+4=9;3+4+5=12;4+5+6=15;5+6+7=18;6+7+8=21;7+8+9=24;8+9+10=27;共有8个不同的和。
分析:因为方框每次框2个数,所以得到不同的和为9个;同理求出每次框3个数的和的个数。关键是理解题意结合实际解决问题。
14、表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同。
1 一共可以框出 个不同的和。
2 (填“能”或“不能”)框出和是64的三个数。
答案:13|不能
解析:解答:①一共能框出不同的和有:15-2=13(个);
②因为框中心的数与左右的数相差2,框中心的数是这3个数的平均数,所以和为3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数。
分析: 考查了简单图形覆盖现象中的规律,本题得到相邻的三个数共有的情况数,及找出框中心数与左右的数的关系:框中心的数是这3个数的平均数是解题的关键。
15、如图是2006年6月的月历,认真观察阴影部分五个数的关系。想一想:如果像这种形式的五个数的和 105,则中间的那个数是 。
答案:21
解析:解答:因为像这种形式五个数的和是105,那么五个数的和是中间的数的5倍,所以中间的数是:105÷5=21,即中间的那个数是21。
分析:观察表中的阴影部分这五个数与中间的数知道五个数的和是中间的数的5倍,解答此题的关键是,根据所给出的阴影部分的数与数的关系,得出规律。
16、如图是一张月历卡,如右图所示,每次同时框出3个数,框出的3个数的和最大是 ,一共可以框出 种不同的和。
答案:84|20
解析:解答:27+28+29=84;
第二行可能的框法:①2、3、4,②3、4、5,③4、5、6,④5、6、7,⑤6、7、8,一共5种,4行的总框法:4×5=20(种),20种框法就有20个不同的和。
分析:和最大时这3个数最大,在这4行中找出最大的3个连续的数相加即可;每一种框法都有不同和,只要求出框法有几种就可以了,每一行的情况相同,只要求出1行的框法再乘4即可。关键是找出数表中的规律。
17、如图,桌面上有A、B、C三个正方形,边长分别为6,8,10;B的一个顶点在A的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是 。
答案:175
解析:解答:A和B盖住面积:
=36+64-9
=91
C盖住的面积:
=100-16
=84
全部的面积:91+84=175
分析:当A,B,C都再不重复时,盖的面积最大.A,B重叠面积是A的;B,C重叠面积是B的,求出A和B能遮住的面积,再求出C能遮住的面积,然后相加。关键是弄清图意。
18、如下图排列,每次框出4个图形,共有 种不同的框法。
答案:7
解析:解答:10-3=7(种)
所以,每次框4个图形可以有7种不同的框法。
分析:主要考查了计数方法的灵活应用,框4个图形时,最后剩下3个图形,再用这组数据的总个数减去最后剩下的3个图形即可解决问题,理解题意是关键。
19、黑色方框每次框住3个数,每次3个数的和不同,一共可以得到 个不同的和。
答案:7
解析:解答:9-2=7(个)
所以每次框出3个数,移动这个框,一共可以得到7个不同的和。
分析:根据计数方法的灵活应用,框3个数字时,最后剩下2个数字,用这组数据的总个数减去最后剩下的2个数字即可解决问题。关键是结合实际理解题意。
20、如图所示,每次框出相邻的三个字母,共有 种不同的框法。
答案:13
解析:解答:15-2=13(种)
所以,共有13种不同的框法。
分析:一共是15个字母,每次框3个连续的字母,那么N和O不能放在最左边,其它的都可以放在最左边,所以一共有15-2种框法。关键是连续的三个字母,注意题目的理解。
四、应用题
21、用形如的长方形去框上面的数,每次同时框出4个数,一共有多少种不同的和?
答案:因为每次圈4个数,所以圈法有:
18-4+1=15(种)
所以,一共可以得到15种不同的圈法。
解析:解答:因为每次圈4个数,所以圈法有:
18-4+1=15(种)
所以,一共可以得到15种不同的圈法。
分析: 4个连续数中最小的数可以分别是1,2,3,4;…;15,16,17,18;所以有:18-4+1=15种不同的圈法。掌握计数方法的灵活应用。
22、有一个音乐钟,每隔一段相等的时间就发生铃声,已知上午9:00,9:40,10:20和11:00发出铃声,那么下面哪个时刻也会发出铃声?
13:30 14:40 15:40 16:00
答案:每隔40分发出铃声,则发出声音的时刻为:11:40;12:20;13时;13:40;14:20;15:00;15:40:16:20;17:00…。所以选项中15:40发出铃声。
分析:因为9时40分-9时=40分,10时20分-9时40分=40分,11时-10时20分=40分,所以由所给时刻得出:每隔40分发出铃声,据此写出下面时刻即可。关键是找出规律再解答。
解析:解答:每隔40分发出铃声,则发出声音的时刻为:11:40;12:20;13时;13:40;14:20;15:00;15:40:16:20;17:00…。所以选项中15:40发出铃声。
分析:因为9时40分-9时=40分,10时20分-9时40分=40分,11时-10时20分=40分,所以由所给时刻得出:每隔40分发出铃声,据此写出下面时刻即可。关键是找出规律再解答。
23、今天学校食堂准备在以下四种荤菜和三种素菜中选择一种素菜和一种荤菜,一共有多少种不同的搭配方法?
答案:3×4=12(种)
答:一共有12种不同的搭配方法。
解析:解答:3×4=12(种)
答:一共有12种不同的搭配方法。
分析:从4种荤菜中选一种有4种选法;从3种素菜中选一种有3种选法;根据乘法原理,可得一共有多少种不同的搭配方法。
24、有4个小朋友,如果每两人之间通一次电话,一共通多少次电话?如果他们互相寄一张贺卡,一共要寄多少张贺卡?
答案:(4-1)×4÷2
=3×4÷2
=6(次);
答:一共通6次电话;
(4-1)×4
=3×4,
=12(次);
答:一共要寄12张贺卡。
解析:解答:(4-1)×4÷2
=3×4÷2
=6(次);
答:一共通6次电话;
(4-1)×4
=3×4,
=12(次);
答:一共要寄12张贺卡。
分析:每个人都要和另外的3个人通一次话,4个人共通话4×3=12次,由于每两人通话,应算作一次,去掉重复的情况,实际只通了12÷2=6次;但是如果他们互相寄一张贺卡,每个人都要得到另外的3个人的3张,由于每两人要互寄,一共要寄:3×4=12张贺卡。注意区别:这两题中“每两人通话一次”和“每两人要互寄一次”的不同。
25、两个自然数相乘,乘积是36的乘法算式有多少个?
答案:36的因数有1、2、3、4、6、9、12、18、36;
1×36=36,36×1=36;
2×18=36,18×2=36;
3×12=36,12×3=36;
4×9=36,9×4=36;
6×6=36;
一共有9个,
答:两个自然数相乘,乘积是36的乘法算式有9个。
解析:解答:36的因数有1、2、3、4、6、9、12、18、36;
1×36=36,36×1=36;
2×18=36,18×2=36;
3×12=36,12×3=36;
4×9=36,9×4=36;
6×6=36;
一共有9个,
答:两个自然数相乘,乘积是36的乘法算式有9个。
分析:根据题意,36的因数有1、2、3、4、6、9、12、18、36,然后再进一步解答。关键是求出36的因数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页)版权所有@21世纪教育网
苏教版数学五年级上册第七单元解决问题的策略同步练习
一、选择题
1、如图,五个正方形重叠,连结点正好是正方形的中点,正方形的边长都是a,如图的周长是 ( )。
A.24a B.18a C. 14a D.12a
答案:D
解析:解答:3a+3a+2a×3=12a
所以,这个图形的周长是12a。
分析:这五个正方形重叠在一起,第一个和最后一个正方形的长度为3a+3a,中间3个正方形的长度是2a×3=6a,把这些长度加起来就是这个图形的周长。掌握图形周长的计算方法。
2、在下面的数表中,每次框出2个数,一共有( )种不同的和。
A. 12 B. 11 C.10
答案:B
解析:解答:数字数:13-2+1=12(个)
不同的和数:12-2+1=11(个)
所以,一共有11种不同的和。
分析:从2到13递增的一行自然数,共有13-2+1=12个数字,每次框出的两个数的和不同,每向右移动一个数字就框出一个和,直到12、13为止,有12-2+1=11个不同的和。掌握数字图片的个数-框的个数+1=不同和的个数。
3、有15个连续的自然数,每次用长方形框出4个连续的自然数,一共有( )种不同的框法。
A.10 B.11 C. 12
答案:C
解析:解答:相邻的4个数有15-4+1=12种情况,则有12种不同的和,即一共有12种不同的框法。
分析:连续的15个自然数写成一行,相邻的4个数有15-4+1=12种情况,则有12种不同的和。得到相邻的4个数的情况数是解题的关键。
4、今年“国庆七日长假”,陆老师想参加“千岛湖双日游”,哪两天去呢,共有多少种不同的选择?( )
A.6种 B.5种 C. 4种 D.3种
答案:A
解析:解答:陆老师可以选择以下的两天去旅游:
10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日,共6种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月7日(最后一天)即可。关键是理解这两天是相邻的两天。
5、今年“国庆七日长假”,王老师想参加“西陵三日游”,王老师共有( )种不同的选择。
A.7 B. 6 C.5 D.4
答案:C
解析:解答:王老师可以选择以下的三天去旅游:
10月1日至10月3日;10月2日至10月4日;10月3日至0月5日;10月4日至10月6日;10月5日至10月7日,共5种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月6、7日(最后两天)即可,关键理解这三天是相邻的三天。
二、判断题
6、操场上20名同学站成一行,老师想从中挑选相邻的4人做游戏,刘强说:“有16种不同的挑选方法”。
答案:错误
解析:解答:20-3=17(种)
分析:20名同学站成一行,老师想从中挑选相邻的4人做游戏,挑到倒数第三名的时候一共有20-3=17种,最后三名就不能挑选了。把相邻的四名同学看做一个整体是解决此题的关键。
7、一个简单图形经过平移、旋转或轴对称,能形成一个较复杂的图形。
答案:正确
解析:解答:一个简单图形经过平移、旋转或轴对称,能形成一个较复杂的图形。
分析:根据图形平移、旋转、轴对称的特征,可以将一个简单的图案,通过这些变化,形成一个较复杂的图形。如,可以将一个图案通过平移形成壁报的花边、将一个梅花瓣通过四次旋转形成一朵梅花。
8、计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再进行计算。
答案:正确
解析:解答:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再根据简单图形的计算公式进行计算。
分析:根据组合图形的面积的计算方法可知:计算组合图形的面积时,可以把组合图形分成几个简单的图形,然后再利用规则图形的面积公式进行计算,关键是把组合图形的面积转化为我们学过的图形的面积,再利用相应的面积公式与基本的数量关系解决问题。
9、有一列图形:○○△□□○○△□□○○△□□…,根据规律,第71个图形是○。
答案:正确
解析:解答:71÷5=14…1;余数是1,那么第71个图形就与第一个相同是○。
分析:把○○△□□看成一组,在一组中前两个图形是○,第三个是△,第四个和第五个是□,共5个;先求出71里面有几组,还余几,再根据余数判断。把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
10、下面一排圆圈共有15个,如果要给相邻的5个涂上红色.一共有11种不同的涂法。
答案:正确
解析:解答:15-5+1=11(种);
所以一共有11种不同的涂法。
分析:把相邻的5个○看作一组,每次覆盖5个,从第一个开始向右平移,每平移一次就可给相邻的5个涂上颜色,到第11个结束;所以共有11种不同的图法。掌握图形覆盖的规律是关键。
三、填空题
11、在如图中,每次框出连续4个自然数,共可得到 个不同的和。
答案:36
解析:解答:40-2+1-3
=39-3
=36
所以,可得到36个不同的和。
分析:一共有40-2+1=39个数,框出就是选连续的,如果按顺序框选,4个连续数中最小的数可以分别是2,3…,37,所以37-2+1=36,一共有36个不同的和。关键是按照顺序依次计数,做到不重复不遗漏。
12、今年“国庆七日长假”,明明想参加“西湖两日游”,哪两日去呢,他共有 种不同的选择。
答案:6
解析:解答:明明可以选择以下的两天去旅游: 10月1日和10月2日;10月2日和10月3日;10月3日和0月4日;10月4日和10月5日;10月5日和10月6日;10月6日和10月7日;共6种选择。
分析:度假的这两天是相邻的两天,只要不把第一天放在10月7日(最后一天)即可。关键是理解这两天是相邻的两天。
13、在下表中每次框出2个相邻的数,一共可以得到 个不同的和;如果每次框出3个相邻的数,一共可以得到 个不同的和。
答案:9|8
解析:解答:如果每次框出2个数,可以得到1+2=3;2+3=5;3+4=7;4+5=9;5+6=11;6+7=13;7+8=15;8+9=17;9+10=19;共有9个不同的和;
每次框出3个数,可以得到1+2+3=6;2+3+4=9;3+4+5=12;4+5+6=15;5+6+7=18;6+7+8=21;7+8+9=24;8+9+10=27;共有8个不同的和。
分析:因为方框每次框2个数,所以得到不同的和为9个;同理求出每次框3个数的和的个数。关键是理解题意结合实际解决问题。
14、表中粗线框中三个数的和是9.在表中移动这个粗线框,可以使每次框出的三个数的和各不相同。
1 一共可以框出 个不同的和。
2 (填“能”或“不能”)框出和是64的三个数。
答案:13|不能
解析:解答:①一共能框出不同的和有:15-2=13(个);
②因为框中心的数与左右的数相差2,框中心的数是这3个数的平均数,所以和为3的倍数,因为64不是3的倍数,所以不能框出和是64的三个数。
分析: 考查了简单图形覆盖现象中的规律,本题得到相邻的三个数共有的情况数,及找出框中心数与左右的数的关系:框中心的数是这3个数的平均数是解题的关键。
15、如图是2006年6月的月历,认真观察阴影部分五个数的关系。想一想:如果像这种形式的五个数的和 105,则中间的那个数是 。
答案:21
解析:解答:因为像这种形式五个数的和是105,那么五个数的和是中间的数的5倍,所以中间的数是:105÷5=21,即中间的那个数是21。
分析:观察表中的阴影部分这五个数与中间的数知道五个数的和是中间的数的5倍,解答此题的关键是,根据所给出的阴影部分的数与数的关系,得出规律。
16、如图是一张月历卡,如右图所示,每次同时框出3个数,框出的3个数的和最大是 ,一共可以框出 种不同的和。
答案:84|20
解析:解答:27+28+29=84;
第二行可能的框法:①2、3、4,②3、4、5,③4、5、6,④5、6、7,⑤6、7、8,一共5种,4行的总框法:4×5=20(种),20种框法就有20个不同的和。
分析:和最大时这3个数最大,在这4行中找出最大的3个连续的数相加即可;每一种框法都有不同和,只要求出框法有几种就可以了,每一行的情况相同,只要求出1行的框法再乘4即可。关键是找出数表中的规律。
17、如图,桌面上有A、B、C三个正方形,边长分别为6,8,10;B的一个顶点在A的中心处,C的一个顶点在B的中心处,这三个正方形最多能盖住的面积是 。
答案:175
解析:解答:A和B盖住面积:
=36+64-9
=91
C盖住的面积:
=100-16
=84
全部的面积:91+84=175
分析:当A,B,C都再不重复时,盖的面积最大.A,B重叠面积是A的;B,C重叠面积是B的,求出A和B能遮住的面积,再求出C能遮住的面积,然后相加。关键是弄清图意。
18、如下图排列,每次框出4个图形,共有 种不同的框法。
答案:7
解析:解答:10-3=7(种)
所以,每次框4个图形可以有7种不同的框法。
分析:主要考查了计数方法的灵活应用,框4个图形时,最后剩下3个图形,再用这组数据的总个数减去最后剩下的3个图形即可解决问题,理解题意是关键。
19、黑色方框每次框住3个数,每次3个数的和不同,一共可以得到 个不同的和。
答案:7
解析:解答:9-2=7(个)
所以每次框出3个数,移动这个框,一共可以得到7个不同的和。
分析:根据计数方法的灵活应用,框3个数字时,最后剩下2个数字,用这组数据的总个数减去最后剩下的2个数字即可解决问题。关键是结合实际理解题意。
20、如图所示,每次框出相邻的三个字母,共有 种不同的框法。
答案:13
解析:解答:15-2=13(种)
所以,共有13种不同的框法。
分析:一共是15个字母,每次框3个连续的字母,那么N和O不能放在最左边,其它的都可以放在最左边,所以一共有15-2种框法。关键是连续的三个字母,注意题目的理解。
四、应用题
21、用形如的长方形去框上面的数,每次同时框出4个数,一共有多少种不同的和?
答案:因为每次圈4个数,所以圈法有:
18-4+1=15(种)
所以,一共可以得到15种不同的圈法。
解析:解答:因为每次圈4个数,所以圈法有:
18-4+1=15(种)
所以,一共可以得到15种不同的圈法。
分析: 4个连续数中最小的数可以分别是1,2,3,4;…;15,16,17,18;所以有:18-4+1=15种不同的圈法。掌握计数方法的灵活应用。
22、有一个音乐钟,每隔一段相等的时间就发生铃声,已知上午9:00,9:40,10:20和11:00发出铃声,那么下面哪个时刻也会发出铃声?
13:30 14:40 15:40 16:00
答案:每隔40分发出铃声,则发出声音的时刻为:11:40;12:20;13时;13:40;14:20;15:00;15:40:16:20;17:00…。所以选项中15:40发出铃声。
分析:因为9时40分-9时=40分,10时20分-9时40分=40分,11时-10时20分=40分,所以由所给时刻得出:每隔40分发出铃声,据此写出下面时刻即可。关键是找出规律再解答。
解析:解答:每隔40分发出铃声,则发出声音的时刻为:11:40;12:20;13时;13:40;14:20;15:00;15:40:16:20;17:00…。所以选项中15:40发出铃声。
分析:因为9时40分-9时=40分,10时20分-9时40分=40分,11时-10时20分=40分,所以由所给时刻得出:每隔40分发出铃声,据此写出下面时刻即可。关键是找出规律再解答。
23、今天学校食堂准备在以下四种荤菜和三种素菜中选择一种素菜和一种荤菜,一共有多少种不同的搭配方法?
答案:3×4=12(种)
答:一共有12种不同的搭配方法。
解析:解答:3×4=12(种)
答:一共有12种不同的搭配方法。
分析:从4种荤菜中选一种有4种选法;从3种素菜中选一种有3种选法;根据乘法原理,可得一共有多少种不同的搭配方法。
24、有4个小朋友,如果每两人之间通一次电话,一共通多少次电话?如果他们互相寄一张贺卡,一共要寄多少张贺卡?
答案:(4-1)×4÷2
=3×4÷2
=6(次);
答:一共通6次电话;
(4-1)×4
=3×4,
=12(次);
答:一共要寄12张贺卡。
解析:解答:(4-1)×4÷2
=3×4÷2
=6(次);
答:一共通6次电话;
(4-1)×4
=3×4,
=12(次);
答:一共要寄12张贺卡。
分析:每个人都要和另外的3个人通一次话,4个人共通话4×3=12次,由于每两人通话,应算作一次,去掉重复的情况,实际只通了12÷2=6次;但是如果他们互相寄一张贺卡,每个人都要得到另外的3个人的3张,由于每两人要互寄,一共要寄:3×4=12张贺卡。注意区别:这两题中“每两人通话一次”和“每两人要互寄一次”的不同。
25、两个自然数相乘,乘积是36的乘法算式有多少个?
答案:36的因数有1、2、3、4、6、9、12、18、36;
1×36=36,36×1=36;
2×18=36,18×2=36;
3×12=36,12×3=36;
4×9=36,9×4=36;
6×6=36;
一共有9个,
答:两个自然数相乘,乘积是36的乘法算式有9个。
解析:解答:36的因数有1、2、3、4、6、9、12、18、36;
1×36=36,36×1=36;
2×18=36,18×2=36;
3×12=36,12×3=36;
4×9=36,9×4=36;
6×6=36;
一共有9个,
答:两个自然数相乘,乘积是36的乘法算式有9个。
分析:根据题意,36的因数有1、2、3、4、6、9、12、18、36,然后再进一步解答。关键是求出36的因数。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 10 页 (共 10 页)版权所有@21世纪教育网
