10.1.1 复数的概念 课件(19张PPT)
文档属性
| 名称 | 10.1.1 复数的概念 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 09:25:14 | ||
图片预览






文档简介
10.1.1 复数的概念
1.了解复数的意义.
2.掌握有关复数的概念、复数的分类,初步掌握虚数单位的概念和性质.(重点)
知识点1:实数系的发展
记数的需要
产生了 自然数
1.为解决实际问题的需要
为了表示各种具有相反意义的量以及满足记数的需要
产生了 负数
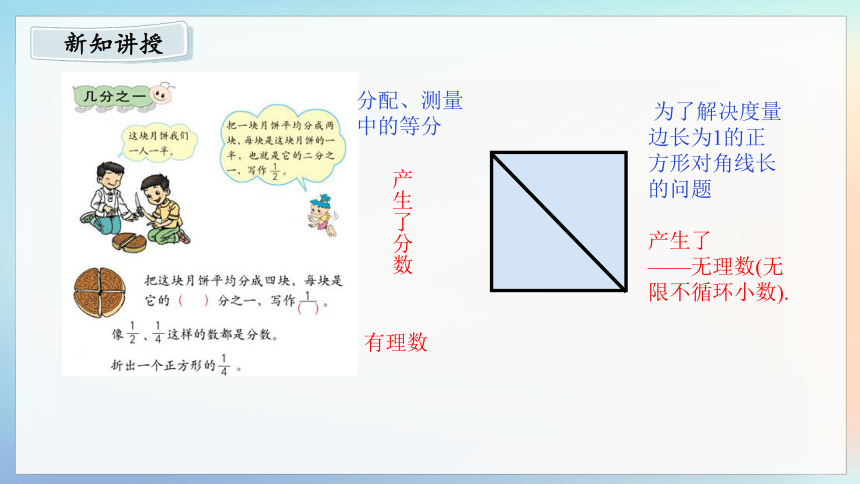
产生了分数
分配、测量中的等分
有理数
为了解决度量边长为1的正方形对角线长的问题
产生了
——无理数(无限不循环小数).
(1)方程????+4=3在自然数集中
?
引入负数;
将自然数系扩充到整数系.
无解
(2)方程2????=5在整数集中
?
引入分数;
将整数系扩充到有理数系.
无解
(3)方程????2=7在有理数集中
?
无解
引入无理数;
将有理数系扩充到实数系.
2.解方程的需要
N
Z
Q
自然数
整数
有理数
数系的扩充
引入新数
R
实数
扩充1
扩充2
扩充3
3.数系扩充后,新数系应遵循原数系的运算律.
扩充后的数集规定的加法运算、乘法运算,与原来数集中规定的加法运算、乘法运算协调一致,且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
知识点2:复数的概念
观察下列三次方程的分解因式,你发现它们都有几个正根?
因式分解:
(1) x3=9x+28→x3-9x-28=0→(x-4)(x2+4x+7)=0;
(2) x3=15x+4→x3-15x-4=0→x3-16x+x-4=4x(x2-16)+(x-4)=(x-4)(x2+4x+1)=0.
均有唯一的正根4.
人们早在16世纪就发现,可以通过求根公式
求解三次方程x3=px+q(p,q均为正实数)的正根
思考1
(1)x3=9x+28;(2)x3=15x+4
(1)????=314+142?32+314?142?32=4
?
(2)由问题1,可知????=32+11?1+32?11?1=4 成立 ,但是不能由公式直接计算得出.
?
你能利用它直接计算,求解上述方程的正根吗?
思考2
如果规定 ,将 按照类似实数的运算法则进行形式计算,你能解释 吗?
所以可以认为32+11?1=2+?1
?
类似地,可以认为32?11?12??1
?
从而形式上有32=11?1+32?11?1=2+?1+2??1=4
?
思考3
一般地,为了使得方程????2=?1有解,人们规定i的平方等于?1.
即????2=?1,并称????为虚数单位.
?
复数的概念:
想一想:怎样表示2与i的和?又该怎样表示3减去i?5与i的乘积可以怎样表示?
2+i;3-i;5i
实数与i进行四则运算时,加法、乘法运算律仍然成立:
(1)实数a与i的和记作a+i,实数0与i的和为i;
(2)实数b与i的积记作bi.
注:实数0与i的积为0,实数1与i的积为i.
在形式上有什么共同特点?
1.复数的代数形式:
其中i 称为虚数单位.
通常用小写字母z表示,即
实部
虚部
复数全体组成的集合叫复数集,复数集通常用大写字母C表示,因此
C={ z| z=a+bi ,a,b∈R}
说一说:下列复数的实部与虚部分别是什么.
-1+2i , 2-3i, 2024 , i , 0 .
2.复数的分类:
复数集C和实数集R之间有什么关系?
思考
例1:分别求实数x的取值,使得复数z=(x-2)+(x+3)i
(1)是实数;(2)是虚数;(3)是纯虚数.
解析:(1)当x+3=0,即x=-3时,复数z是实数.
(2)当x+3≠0,即x≠-3时,复数z是虚数.
(3)当x-2=0,且x+3≠0,即x=2时,复数z是纯虚数.
2.复数相等:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个复数只能说相等或不相等,而不能比较大小.
????=????且????=????
?
????+????????=????+????????
?
1)????+????????=0(????,????∈????)?????=0且????=0
?
例2:分别求满足下列关系式的实数????与????的值
?
(1)(????+2????)?????=6????+(?????????)????;
(2)(????+????+1)?(?????????+2)????=0
?
解析:(1)根据复数相等的定义,得
(2)根据复数等于0得充要条件,得
????+2????=6?????1=?????????
?
解这个方程组,得????=23,????=53
?
????+????+1=0?(?????????+2)=0
?
解这个方程组,得????=?32,????=12
?
D
A
3.复数 ,当实数m= 时,z为纯虚数;当实数m= 时,z为零.
-2
1
1.虚数单位i的引入.
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
1.了解复数的意义.
2.掌握有关复数的概念、复数的分类,初步掌握虚数单位的概念和性质.(重点)
知识点1:实数系的发展
记数的需要
产生了 自然数
1.为解决实际问题的需要
为了表示各种具有相反意义的量以及满足记数的需要
产生了 负数
产生了分数
分配、测量中的等分
有理数
为了解决度量边长为1的正方形对角线长的问题
产生了
——无理数(无限不循环小数).
(1)方程????+4=3在自然数集中
?
引入负数;
将自然数系扩充到整数系.
无解
(2)方程2????=5在整数集中
?
引入分数;
将整数系扩充到有理数系.
无解
(3)方程????2=7在有理数集中
?
无解
引入无理数;
将有理数系扩充到实数系.
2.解方程的需要
N
Z
Q
自然数
整数
有理数
数系的扩充
引入新数
R
实数
扩充1
扩充2
扩充3
3.数系扩充后,新数系应遵循原数系的运算律.
扩充后的数集规定的加法运算、乘法运算,与原来数集中规定的加法运算、乘法运算协调一致,且加法和乘法都满足交换律和结合律,乘法对加法满足分配律.
知识点2:复数的概念
观察下列三次方程的分解因式,你发现它们都有几个正根?
因式分解:
(1) x3=9x+28→x3-9x-28=0→(x-4)(x2+4x+7)=0;
(2) x3=15x+4→x3-15x-4=0→x3-16x+x-4=4x(x2-16)+(x-4)=(x-4)(x2+4x+1)=0.
均有唯一的正根4.
人们早在16世纪就发现,可以通过求根公式
求解三次方程x3=px+q(p,q均为正实数)的正根
思考1
(1)x3=9x+28;(2)x3=15x+4
(1)????=314+142?32+314?142?32=4
?
(2)由问题1,可知????=32+11?1+32?11?1=4 成立 ,但是不能由公式直接计算得出.
?
你能利用它直接计算,求解上述方程的正根吗?
思考2
如果规定 ,将 按照类似实数的运算法则进行形式计算,你能解释 吗?
所以可以认为32+11?1=2+?1
?
类似地,可以认为32?11?12??1
?
从而形式上有32=11?1+32?11?1=2+?1+2??1=4
?
思考3
一般地,为了使得方程????2=?1有解,人们规定i的平方等于?1.
即????2=?1,并称????为虚数单位.
?
复数的概念:
想一想:怎样表示2与i的和?又该怎样表示3减去i?5与i的乘积可以怎样表示?
2+i;3-i;5i
实数与i进行四则运算时,加法、乘法运算律仍然成立:
(1)实数a与i的和记作a+i,实数0与i的和为i;
(2)实数b与i的积记作bi.
注:实数0与i的积为0,实数1与i的积为i.
在形式上有什么共同特点?
1.复数的代数形式:
其中i 称为虚数单位.
通常用小写字母z表示,即
实部
虚部
复数全体组成的集合叫复数集,复数集通常用大写字母C表示,因此
C={ z| z=a+bi ,a,b∈R}
说一说:下列复数的实部与虚部分别是什么.
-1+2i , 2-3i, 2024 , i , 0 .
2.复数的分类:
复数集C和实数集R之间有什么关系?
思考
例1:分别求实数x的取值,使得复数z=(x-2)+(x+3)i
(1)是实数;(2)是虚数;(3)是纯虚数.
解析:(1)当x+3=0,即x=-3时,复数z是实数.
(2)当x+3≠0,即x≠-3时,复数z是虚数.
(3)当x-2=0,且x+3≠0,即x=2时,复数z是纯虚数.
2.复数相等:如果两个复数的实部和虚部分别相等,那么我们就说这两个复数相等.
注:
2) 一般来说,两个复数只能说相等或不相等,而不能比较大小.
????=????且????=????
?
????+????????=????+????????
?
1)????+????????=0(????,????∈????)?????=0且????=0
?
例2:分别求满足下列关系式的实数????与????的值
?
(1)(????+2????)?????=6????+(?????????)????;
(2)(????+????+1)?(?????????+2)????=0
?
解析:(1)根据复数相等的定义,得
(2)根据复数等于0得充要条件,得
????+2????=6?????1=?????????
?
解这个方程组,得????=23,????=53
?
????+????+1=0?(?????????+2)=0
?
解这个方程组,得????=?32,????=12
?
D
A
3.复数 ,当实数m= 时,z为纯虚数;当实数m= 时,z为零.
-2
1
1.虚数单位i的引入.
2.复数有关概念:
复数的代数形式:
复数的实部 、虚部
复数相等
虚数、纯虚数
