11.2 平面的基本事实与推论 课件(共24张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.2 平面的基本事实与推论 课件(共24张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览






文档简介
11.2 平面的基本事实与推论
1.了解平面的概念,掌握平面的画法及表示方法.
2.掌握平面的基本事实及推论,能用符号语言描述空间点、直线、平面之间的位置关系.
3.能用图形、文字、符号三种语言描述三个基本事实,并能解决空间线面的位置关系问题.
复习导入
在初中几何中,学习过哪些点与直线的基本事实?
(1)连接两点的线中,线段最短;
(2)过两点有一条直线,并且只有一条直线.
也可简单地说成
“两点确定一条直线”
事实上,通过指定的一个点可以作无数条直线;通过指定的三个点,不一定能作一条直线.所以(2)是确定直线的依据.
观察如图的凳子,把凳子看成一个平面.
三个点
无数个、无数个.
有多少个平面能通过空间中指定的一点?有多少平面能通过空间中指定的两点?
如果把一个平面固定在空间中,至少需要固定几个点?
经过任意三点都能确定一个平面吗?由此可得什么结论?
不一定
探究1 平面的基本性质
思考1
思考2
思考3
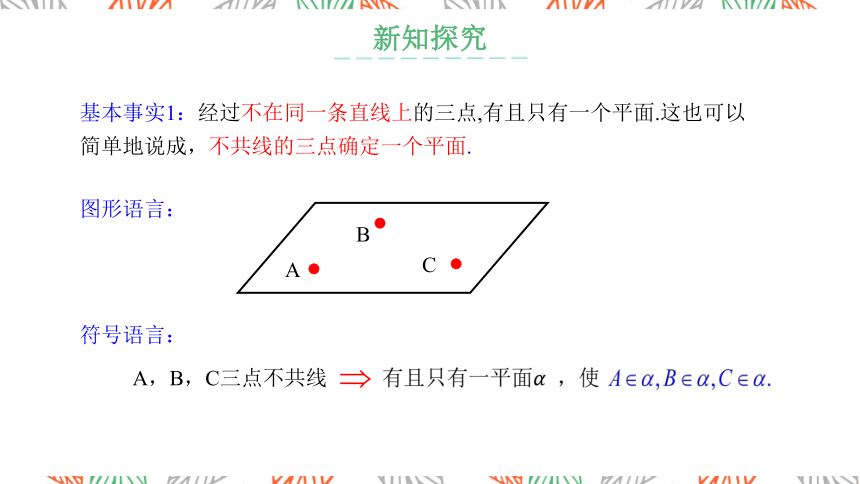
基本事实1:经过不在同一条直线上的三点,有且只有一个平面.这也可以简单地说成,不共线的三点确定一个平面.
图形语言:
A
B
C
符号语言:
A,B,C三点不共线
有且只有一平面???? ,使
?
(1)基本事实1是确定平面的条件,也是证明两个平面重合的依据.
对于基本事实1:
(2)确定平面的条件是将空间图形问题转化为平面图形问题来解决的重要依据,也为证明直线共面问题提供了依据.
(3)深刻理解“有且只有”的含义,这里的“有”是说平面存在,“只有”是说平面唯一,“有且只有”强调平面存在并且唯一这两方面.
经过不在同一条直线上的三点,有且只有一个平面.这也可以简单地说成,不共线的三点确定一个平面.
(1)经过同一直线上三点可以确定______个平面.
(2)经过一点可以确定______个平面.
(3)经过二点可以确定______个平面.
无数
无数
无数
0或1
(4)经过不在同一条直线上的四点可以确定_______个平面.
练一练
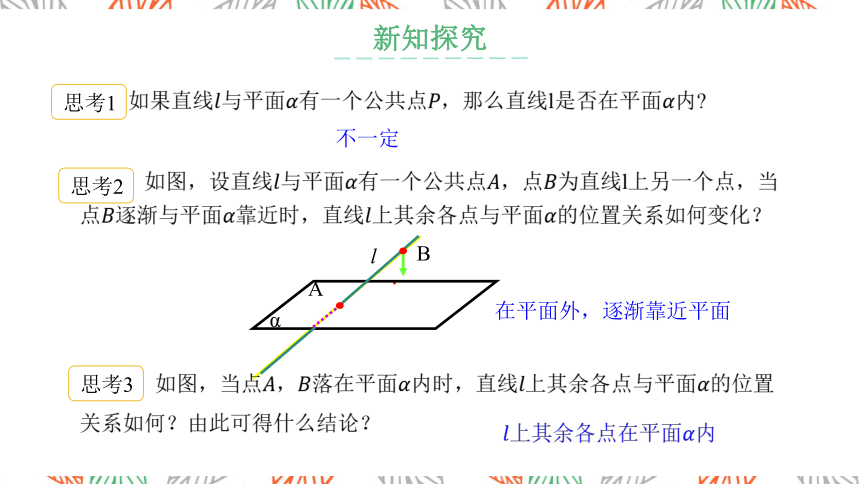
如果直线????与平面????有一个公共点????,那么直线l是否在平面????内?
?
不一定
如图,设直线????与平面????有一个公共点????,点????为直线l上另一个点,当点????逐渐与平面????靠近时,直线????上其余各点与平面????的位置关系如何变化?
?
在平面外,逐渐靠近平面
.
l
A
B
α
如图,当点????,????落在平面????内时,直线????上其余各点与平面????的位置关系如何?由此可得什么结论?
?
????上其余各点在平面????内
?
思考1
思考2
思考3
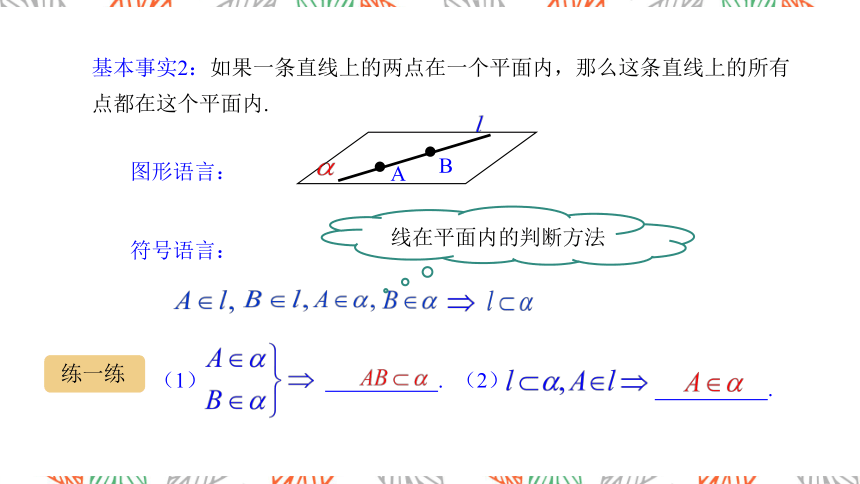
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内.
图形语言:
符号语言:
B
A
线在平面内的判断方法
(1)
.
(2)
.
练一练
作用1: 作为判断和证明直线是否在平面内的依据,即只需要看直线上是否有两个点在平面内就可以了.
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内.
作用2: 可以用来检验某一个面是否为平面,检验的方法为:把一条直线在面内旋转,固定两个点在面内后,如果其他点也在面内,则该面为平面.
例如,球面不是一个平面,因为球面上任意两点所确定的直线中,只有两个点在球面上.
当用裁纸刀裁纸时,可以认为刀锋是在一个平面内运动的.
裁纸刀裁出的是什么样的痕迹?
两个平面相交时,公共点具有什么特点?
直线
如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的平面是否只相交于一点B?为什么?
B
不是,因为平面是无限延伸的.
公共点在一条直线上(共线).
思考1
思考2
思考3
基本事实3:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.
符号语言:P∈(α∩β) α∩β=l,且P∈l.
图形语言:
作用:
(1)用来判定两平面是否相交.
(2)画两个相交平面的交线.
(3)确定三点共线或三线共点.
(1)基本性质3反映了平面与平面的位置关系,只要“不重合两面共一点”,就有“两面共一线,且过这一点,线唯一”.
(2) 从集合的角度看,对于不重合的两个平面,只要它们有公共点,它们就是相交的位置关系,交集是一条直线.
对于基本事实3:
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.两两相交且不共点的三条直线确定一个平面
D.四边形确定一个平面
C
练一练
探究2 平面的基本性质的推论
文字语言 :经过一条直线和直线外的一点,有且只有一个平面.
推论1:
图形语言:
α
A
a
.
符号语言:
????与A 共属于平面????且平面????唯一.
?
????是任意一条直线
?
点A ????
?
推论2:
文字语言:经过两条相交直线,有且只有一个平面.
图形语言:
推论3:
文字语言: 经过两条平行直线,有且只有一个平面.
图形语言:
????
?
a
b
证明:两两相交且不过同一个点的3条直线必在同一个平面内.
证明:设直线AB,BC,AC两两相交,交点分别是A,B,C.
显然,A,B,C3点不共线,因此它们能确定一个平面α.
因为A∈α,B∈α, 那么直线AB?α.
同理 AC?α,BC?α.
即直线AB,BC,AC都在平面α内.
例1
解析
证明点、线共面的常用方法:
(1)“纳入法”:先由部分点、线确定一个面,再证其余的点、线都在这个平面内;
(2)“同一法”:先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合;
(3)“反证法”:假设不共面,结合题设推出矛盾.
如图,已知E,F,G,H分别是四面体A-BCD的棱AB,BC,CD,DA的中点,求证:E,F,G,H四点共面
证明:在△ABD中,∵E,H分别是AB,AD的中点,∴EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.
跟踪训练
如图所示的正方体ABCD-A1B1C1D1中,E是棱CC1上的一点,试说明D1,A,E 3点确定的平面与平面ABCD相交,并画出这两个平面的交线.
因为A∈面D1AE,A∈面ABCD,
所以面D1AE∩ABCD≠?,即面D1AE与面ABCD相交.
延长D1E与DC,设它们相交于F,如图所示,则:
?
F∈直线D1E,直线D1E?面D1AE,
F∈直线DC,直线DC?面ABCD,
则F∈面D1AE∩面ABCD,从而AF为面D1AE与面ABCD的交线,如图所示.
例2
解析
1.下列说法正确的是( )
A.三点可以确定一个平面
B.若直线上有一个点在一个平面内,则这条直线在这个平面内
C.把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面相交于一点
D.如果两个平面有三个不共线的点,那么这两个平面重合
D
2.
1.了解平面的概念,掌握平面的画法及表示方法.
2.掌握平面的基本事实及推论,能用符号语言描述空间点、直线、平面之间的位置关系.
3.能用图形、文字、符号三种语言描述三个基本事实,并能解决空间线面的位置关系问题.
复习导入
在初中几何中,学习过哪些点与直线的基本事实?
(1)连接两点的线中,线段最短;
(2)过两点有一条直线,并且只有一条直线.
也可简单地说成
“两点确定一条直线”
事实上,通过指定的一个点可以作无数条直线;通过指定的三个点,不一定能作一条直线.所以(2)是确定直线的依据.
观察如图的凳子,把凳子看成一个平面.
三个点
无数个、无数个.
有多少个平面能通过空间中指定的一点?有多少平面能通过空间中指定的两点?
如果把一个平面固定在空间中,至少需要固定几个点?
经过任意三点都能确定一个平面吗?由此可得什么结论?
不一定
探究1 平面的基本性质
思考1
思考2
思考3
基本事实1:经过不在同一条直线上的三点,有且只有一个平面.这也可以简单地说成,不共线的三点确定一个平面.
图形语言:
A
B
C
符号语言:
A,B,C三点不共线
有且只有一平面???? ,使
?
(1)基本事实1是确定平面的条件,也是证明两个平面重合的依据.
对于基本事实1:
(2)确定平面的条件是将空间图形问题转化为平面图形问题来解决的重要依据,也为证明直线共面问题提供了依据.
(3)深刻理解“有且只有”的含义,这里的“有”是说平面存在,“只有”是说平面唯一,“有且只有”强调平面存在并且唯一这两方面.
经过不在同一条直线上的三点,有且只有一个平面.这也可以简单地说成,不共线的三点确定一个平面.
(1)经过同一直线上三点可以确定______个平面.
(2)经过一点可以确定______个平面.
(3)经过二点可以确定______个平面.
无数
无数
无数
0或1
(4)经过不在同一条直线上的四点可以确定_______个平面.
练一练
如果直线????与平面????有一个公共点????,那么直线l是否在平面????内?
?
不一定
如图,设直线????与平面????有一个公共点????,点????为直线l上另一个点,当点????逐渐与平面????靠近时,直线????上其余各点与平面????的位置关系如何变化?
?
在平面外,逐渐靠近平面
.
l
A
B
α
如图,当点????,????落在平面????内时,直线????上其余各点与平面????的位置关系如何?由此可得什么结论?
?
????上其余各点在平面????内
?
思考1
思考2
思考3
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内.
图形语言:
符号语言:
B
A
线在平面内的判断方法
(1)
.
(2)
.
练一练
作用1: 作为判断和证明直线是否在平面内的依据,即只需要看直线上是否有两个点在平面内就可以了.
基本事实2:如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内.
作用2: 可以用来检验某一个面是否为平面,检验的方法为:把一条直线在面内旋转,固定两个点在面内后,如果其他点也在面内,则该面为平面.
例如,球面不是一个平面,因为球面上任意两点所确定的直线中,只有两个点在球面上.
当用裁纸刀裁纸时,可以认为刀锋是在一个平面内运动的.
裁纸刀裁出的是什么样的痕迹?
两个平面相交时,公共点具有什么特点?
直线
如图,把三角板的一个角立在课桌面上,三角板所在的平面与桌面所在的平面是否只相交于一点B?为什么?
B
不是,因为平面是无限延伸的.
公共点在一条直线上(共线).
思考1
思考2
思考3
基本事实3:如果不重合的两个平面有一个公共点,那么它们有且只有一条过这个点的公共直线.
符号语言:P∈(α∩β) α∩β=l,且P∈l.
图形语言:
作用:
(1)用来判定两平面是否相交.
(2)画两个相交平面的交线.
(3)确定三点共线或三线共点.
(1)基本性质3反映了平面与平面的位置关系,只要“不重合两面共一点”,就有“两面共一线,且过这一点,线唯一”.
(2) 从集合的角度看,对于不重合的两个平面,只要它们有公共点,它们就是相交的位置关系,交集是一条直线.
对于基本事实3:
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.两两相交且不共点的三条直线确定一个平面
D.四边形确定一个平面
C
练一练
探究2 平面的基本性质的推论
文字语言 :经过一条直线和直线外的一点,有且只有一个平面.
推论1:
图形语言:
α
A
a
.
符号语言:
????与A 共属于平面????且平面????唯一.
?
????是任意一条直线
?
点A ????
?
推论2:
文字语言:经过两条相交直线,有且只有一个平面.
图形语言:
推论3:
文字语言: 经过两条平行直线,有且只有一个平面.
图形语言:
????
?
a
b
证明:两两相交且不过同一个点的3条直线必在同一个平面内.
证明:设直线AB,BC,AC两两相交,交点分别是A,B,C.
显然,A,B,C3点不共线,因此它们能确定一个平面α.
因为A∈α,B∈α, 那么直线AB?α.
同理 AC?α,BC?α.
即直线AB,BC,AC都在平面α内.
例1
解析
证明点、线共面的常用方法:
(1)“纳入法”:先由部分点、线确定一个面,再证其余的点、线都在这个平面内;
(2)“同一法”:先由其中一部分点、线确定一个平面α,其余点、线确定另一个平面β,再证平面α与β重合;
(3)“反证法”:假设不共面,结合题设推出矛盾.
如图,已知E,F,G,H分别是四面体A-BCD的棱AB,BC,CD,DA的中点,求证:E,F,G,H四点共面
证明:在△ABD中,∵E,H分别是AB,AD的中点,∴EH∥BD.
同理FG∥BD,则EH∥FG.
故E,F,G,H四点共面.
跟踪训练
如图所示的正方体ABCD-A1B1C1D1中,E是棱CC1上的一点,试说明D1,A,E 3点确定的平面与平面ABCD相交,并画出这两个平面的交线.
因为A∈面D1AE,A∈面ABCD,
所以面D1AE∩ABCD≠?,即面D1AE与面ABCD相交.
延长D1E与DC,设它们相交于F,如图所示,则:
?
F∈直线D1E,直线D1E?面D1AE,
F∈直线DC,直线DC?面ABCD,
则F∈面D1AE∩面ABCD,从而AF为面D1AE与面ABCD的交线,如图所示.
例2
解析
1.下列说法正确的是( )
A.三点可以确定一个平面
B.若直线上有一个点在一个平面内,则这条直线在这个平面内
C.把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面相交于一点
D.如果两个平面有三个不共线的点,那么这两个平面重合
D
2.
