9.1.1 正弦定理 课件(共25张PPT)2024-2025学年高一数学人教B版(2019)必修第四册
文档属性
| 名称 | 9.1.1 正弦定理 课件(共25张PPT)2024-2025学年高一数学人教B版(2019)必修第四册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1023.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览







文档简介
9.1.1 正弦定理
1.了解正弦定理的推导过程.
2.掌握正弦定理,并能解决一些简单的三角形度量问题.(重点、难点)
4.在直角三角形ABC中,C=900,则 .
复习回顾
1.角的关系:
2.边的关系:
3.边角关系:
A
C
B
C
B
A
你还记得三角形的哪些边、角关系?
两边之和大于第三边,
两边之差小于第三边
大角对大边,大边对大角;
小角对小边,小边对小角;
等边对等角
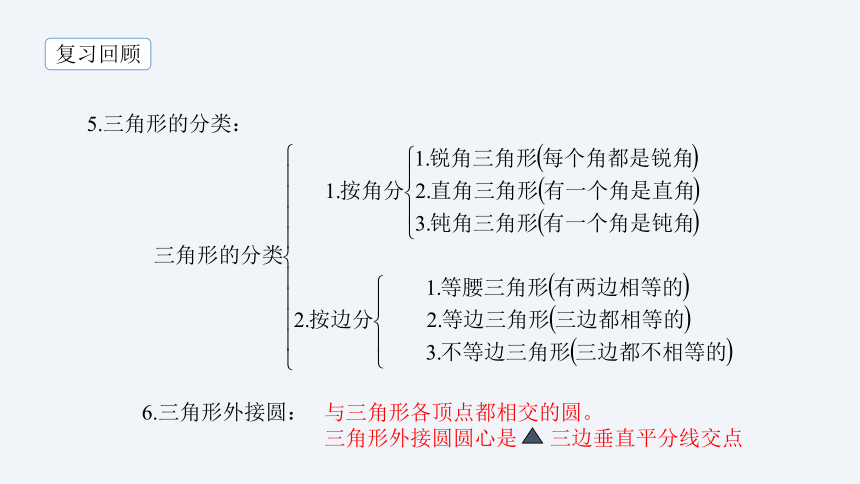
5.三角形的分类:
6.三角形外接圆:
与三角形各顶点都相交的圆。
三角形外接圆圆心是 三边垂直平分线交点
复习回顾
7.三角形全等条件
(1)边角边:两边及其夹角对应相百等,这两个三角形全等.简写成(S.A.S)
(2)角边角:两角及其度夹边对应相等,这两个三角形全等.简写成(A.S.A)
(3)角角边:两角及其一角所对的边对应相等,这两个三角形全等.简写成:(A.A.S)
(4)边边边:三条边分别对应相等,这两个三角形答全等.简写成:(S.S.S)
(5)直角边斜边:斜边和其中的一条直角边分别对应相等,这两个三角形全等.简写成:(H.L)
复习回顾
情境与问题
在现代生活中,得益于科技的发展.距离的测量能 借助红外测距仪、激光测距仪等工具直接完成.不过,在这些工具没有出现以前.你知道人们是怎样间接获得两点间的距离的吗?
为了方便,将△ABC 3个内角A,B, C 所对的边分别记为a,b,c.
如图所示.若想知道河对岸的一点A与岸边—点H之间的距离,而且已经测量出了BC的长,也想办法得到了∠ABC与∠ACB的大小,你能借助这3个量,求出AB的长吗?
b
????
?
c
在这样的约定下,情境中的问题可以转化为:已知a,B,C,如何求c.
(1) 如图所示,已知△ABC 中,“a=5,b=3, C= ,你能求出这个三角形的面积吗?
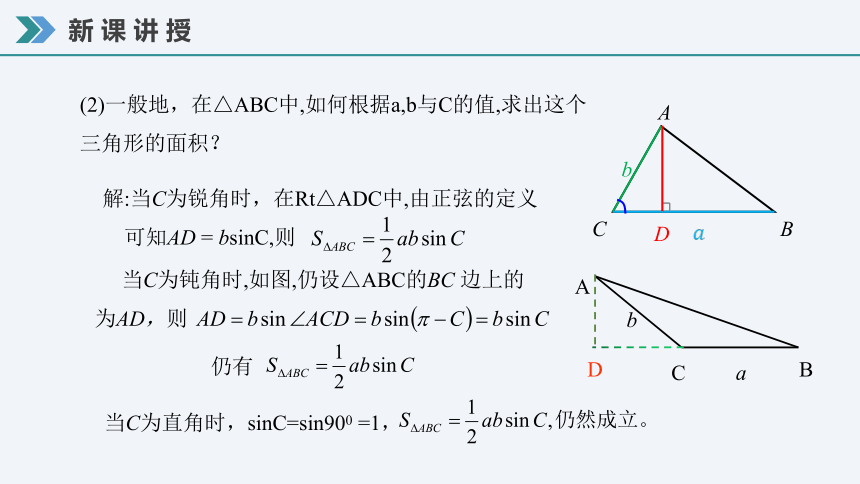
(2) 一般地,在△ABC中,如何根据a,b与C的值,求出这个三角形的面积?
解:(1)如图所示,在中△ABC中,过点A作BC边上的高AD,
在Rt△ADC中,由正弦的定义可知 AD = bsinC,
A
B
C
b
????
?
D
想一想:
因此所求三角形的面积为
(2)一般地,在△ABC中,如何根据a,b与C的值,求出这个三角形的面积?
解:当C为锐角时,在Rt△ADC中,由正弦的定义
可知AD = bsinC,则
当C为钝角时,如图,仍设△ABC的BC 边上的
为AD,则
当C为直角时,sinC=sin900 =1,
仍有
A
B
C
b
????
?
D
A
B
C
a
b
D
1.三角形面积公式
在△ABC中,用上述方法,可以推导出以下公式: ①已知b,c与A的值,则
②已知a,c与B的值,则
一般地,记△ABC的面积为S,则
知识归纳
2.正弦定理
由此三角形面积公式
可得
这就是正弦定理:在三角形中,各边的长和它所对角的正弦的比相等。
可知
如图作△ABC外接圆,R为△ABC外接圆半径CD为外接圆O的直径,连接BD,则∠A=∠D
A
B
C
a
b
c
O
D
用三角形外接圆法推导正弦定理
(R为△ABC外接圆半径)
从而证得
直径所对的圆周角是直角,即∠CBD为直角
正弦定理及其变形
在?ABC中,角A,B,C,所对应的边分别为a,b,c,三角形外接圆半径为R,正弦定理:
变形:
C
A
a
B
b
c
左右分别相加做比值
适用于任何三角形
例1 已知△ABC中,B=75°,C=60°,a =10,求 c.
解:由已知可得 A=180°- B-C = 180°-75°-60°=45°.
由正向定理可知
所以
注意: 在一个三角形中,已知两个角与一条边,就可求这个三角形的另外一个角,然后由正弦定理可求出该三角形其他的两条边.
这与初中所学的三角形全等的判定定理AAS(或ASA)一致.
把三角形3个角与3条边都称为三角形的元素。已知三角形的若干元素求其他元素称为解三角形。
题型1:已知两角和任一边,求其他两边和其余一角.
例2:
解:
注意:根据以上解答可知.右图中的(1)(2)都满足例2的条件.事实上,这与我们初屮所学的SSA不能作为:角形全等的判定定理一致.
题型2:已知两边和其中一边的对角,求另一边和其余两角.
B
A
C
C
B
A
(1)
(2)
例3:
解:
题型3:已知两边和其中一边的对角,求另一边和其余两角.
例4:
解:
题型4:已知两边和其中一边的对角,求另一边和其余两角.
例2、例3、例4都是两边及一边的对角,此时三角形形状不确定,所以解的个数不确定.题中最终有几个解是由已知条件所确定的,明确所求角的范围是解题的关键.
方法归纳
探究三角形解的个数的确定因素
1.画图法:以已知角的对边为半径画弧,通过与邻边的交点个数判断解的个数。
①若无交点,则无解;
②若有一个交点,则有一个解;
③若有两个交点,则有两个解;
④若交点重合,虽然有两个交点,但只能算作一个解。
2.公式法:运用正弦定理进行求解。
①a=bsinA,△=0,则一个解;
②a>bsinA,△>0,则两个解;
③a<bsinA,△<0,则无解。
{5940675A-B579-460E-94D1-54222C63F5DA}A
为
锐
角
图形
关系
????????=????sin????
????sin????????≥????
解的个数
0
1
2
1
A
为
钝
角
或
直
角
图形
关系
????≤????
????≤????
????>????
????>????
解的个数
0
0
1
1
{5940675A-B579-460E-94D1-54222C63F5DA}A
为
锐
角
图形
关系
解的个数
0
1
2
1
A
为
钝
角
或
直
角
图形
关系
解的个数
0
0
1
1
练一练:
1.下列关于△ABC的说法正确的是( )
A.若a=7,b=14,A=30°,则B有两解
B.若a=30,b=25,A=150°,则B只有一解
C.若a=6,b=9,A=45°,则B有两解
D.若b=9,c=10,B=60°,则C无解
B
A项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????=14×127=1,∴B=90°,即只有一解,A项错误;
?
B项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????
25×1230<1,又∵A为钝角,B只有一解,故B项正确;
?
C项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????=9×226>1,又∵B不存在,即一解,C项错误;
?
D项中,∵???????????????? ????=???????????????? ????,∴sin C=???????????????? ????????=10×329<1,又∵b?
解析:
例5:
证明:
代入
角化边
解:由正弦定理可知
因此
因此,?ABC为等腰三角形或直角三角形。
边化角
代入
练一练:2.
1.利用正弦定理把已知条件转化为边边关系,通过因式分解、 配方等得出边的相应关系,从而判断三角形的形状;
2.利用正弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.
注意:在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
知识归纳
利用正弦定理判断三角形形状的两种方法:
例6:如图所示,在?ABC中,已知 的角分线AD与边BC相交于点D,求证:
证明:如图,设
则由题意可知
在?ABD和?ADC中,分别应用正弦定理,可得
两式相除即可得
内角平分线定理
一题多解:本题也可用面积公式或平面几何知识证明!
D
A
B
C
β
β
α
π–α
1.正弦定理:
正弦定理常用变形:
2.三角形面积公式:
3.正弦定理的应用范围
(1)已知两角和任一边,求其他两边和其余一角.
(2)已知两边和其中一边的对角,求另一边和其余两角.
本节课你学到了哪些知识?
1.了解正弦定理的推导过程.
2.掌握正弦定理,并能解决一些简单的三角形度量问题.(重点、难点)
4.在直角三角形ABC中,C=900,则 .
复习回顾
1.角的关系:
2.边的关系:
3.边角关系:
A
C
B
C
B
A
你还记得三角形的哪些边、角关系?
两边之和大于第三边,
两边之差小于第三边
大角对大边,大边对大角;
小角对小边,小边对小角;
等边对等角
5.三角形的分类:
6.三角形外接圆:
与三角形各顶点都相交的圆。
三角形外接圆圆心是 三边垂直平分线交点
复习回顾
7.三角形全等条件
(1)边角边:两边及其夹角对应相百等,这两个三角形全等.简写成(S.A.S)
(2)角边角:两角及其度夹边对应相等,这两个三角形全等.简写成(A.S.A)
(3)角角边:两角及其一角所对的边对应相等,这两个三角形全等.简写成:(A.A.S)
(4)边边边:三条边分别对应相等,这两个三角形答全等.简写成:(S.S.S)
(5)直角边斜边:斜边和其中的一条直角边分别对应相等,这两个三角形全等.简写成:(H.L)
复习回顾
情境与问题
在现代生活中,得益于科技的发展.距离的测量能 借助红外测距仪、激光测距仪等工具直接完成.不过,在这些工具没有出现以前.你知道人们是怎样间接获得两点间的距离的吗?
为了方便,将△ABC 3个内角A,B, C 所对的边分别记为a,b,c.
如图所示.若想知道河对岸的一点A与岸边—点H之间的距离,而且已经测量出了BC的长,也想办法得到了∠ABC与∠ACB的大小,你能借助这3个量,求出AB的长吗?
b
????
?
c
在这样的约定下,情境中的问题可以转化为:已知a,B,C,如何求c.
(1) 如图所示,已知△ABC 中,“a=5,b=3, C= ,你能求出这个三角形的面积吗?
(2) 一般地,在△ABC中,如何根据a,b与C的值,求出这个三角形的面积?
解:(1)如图所示,在中△ABC中,过点A作BC边上的高AD,
在Rt△ADC中,由正弦的定义可知 AD = bsinC,
A
B
C
b
????
?
D
想一想:
因此所求三角形的面积为
(2)一般地,在△ABC中,如何根据a,b与C的值,求出这个三角形的面积?
解:当C为锐角时,在Rt△ADC中,由正弦的定义
可知AD = bsinC,则
当C为钝角时,如图,仍设△ABC的BC 边上的
为AD,则
当C为直角时,sinC=sin900 =1,
仍有
A
B
C
b
????
?
D
A
B
C
a
b
D
1.三角形面积公式
在△ABC中,用上述方法,可以推导出以下公式: ①已知b,c与A的值,则
②已知a,c与B的值,则
一般地,记△ABC的面积为S,则
知识归纳
2.正弦定理
由此三角形面积公式
可得
这就是正弦定理:在三角形中,各边的长和它所对角的正弦的比相等。
可知
如图作△ABC外接圆,R为△ABC外接圆半径CD为外接圆O的直径,连接BD,则∠A=∠D
A
B
C
a
b
c
O
D
用三角形外接圆法推导正弦定理
(R为△ABC外接圆半径)
从而证得
直径所对的圆周角是直角,即∠CBD为直角
正弦定理及其变形
在?ABC中,角A,B,C,所对应的边分别为a,b,c,三角形外接圆半径为R,正弦定理:
变形:
C
A
a
B
b
c
左右分别相加做比值
适用于任何三角形
例1 已知△ABC中,B=75°,C=60°,a =10,求 c.
解:由已知可得 A=180°- B-C = 180°-75°-60°=45°.
由正向定理可知
所以
注意: 在一个三角形中,已知两个角与一条边,就可求这个三角形的另外一个角,然后由正弦定理可求出该三角形其他的两条边.
这与初中所学的三角形全等的判定定理AAS(或ASA)一致.
把三角形3个角与3条边都称为三角形的元素。已知三角形的若干元素求其他元素称为解三角形。
题型1:已知两角和任一边,求其他两边和其余一角.
例2:
解:
注意:根据以上解答可知.右图中的(1)(2)都满足例2的条件.事实上,这与我们初屮所学的SSA不能作为:角形全等的判定定理一致.
题型2:已知两边和其中一边的对角,求另一边和其余两角.
B
A
C
C
B
A
(1)
(2)
例3:
解:
题型3:已知两边和其中一边的对角,求另一边和其余两角.
例4:
解:
题型4:已知两边和其中一边的对角,求另一边和其余两角.
例2、例3、例4都是两边及一边的对角,此时三角形形状不确定,所以解的个数不确定.题中最终有几个解是由已知条件所确定的,明确所求角的范围是解题的关键.
方法归纳
探究三角形解的个数的确定因素
1.画图法:以已知角的对边为半径画弧,通过与邻边的交点个数判断解的个数。
①若无交点,则无解;
②若有一个交点,则有一个解;
③若有两个交点,则有两个解;
④若交点重合,虽然有两个交点,但只能算作一个解。
2.公式法:运用正弦定理进行求解。
①a=bsinA,△=0,则一个解;
②a>bsinA,△>0,则两个解;
③a<bsinA,△<0,则无解。
{5940675A-B579-460E-94D1-54222C63F5DA}A
为
锐
角
图形
关系
????????=????sin????
????sin????????≥????
解的个数
0
1
2
1
A
为
钝
角
或
直
角
图形
关系
????≤????
????≤????
????>????
????>????
解的个数
0
0
1
1
{5940675A-B579-460E-94D1-54222C63F5DA}A
为
锐
角
图形
关系
解的个数
0
1
2
1
A
为
钝
角
或
直
角
图形
关系
解的个数
0
0
1
1
练一练:
1.下列关于△ABC的说法正确的是( )
A.若a=7,b=14,A=30°,则B有两解
B.若a=30,b=25,A=150°,则B只有一解
C.若a=6,b=9,A=45°,则B有两解
D.若b=9,c=10,B=60°,则C无解
B
A项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????=14×127=1,∴B=90°,即只有一解,A项错误;
?
B项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????
25×1230<1,又∵A为钝角,B只有一解,故B项正确;
?
C项中,∵???????????????? ????=???????????????? ????,∴sin B=???????????????? ????????=9×226>1,又∵B不存在,即一解,C项错误;
?
D项中,∵???????????????? ????=???????????????? ????,∴sin C=???????????????? ????????=10×329<1,又∵b
解析:
例5:
证明:
代入
角化边
解:由正弦定理可知
因此
因此,?ABC为等腰三角形或直角三角形。
边化角
代入
练一练:2.
1.利用正弦定理把已知条件转化为边边关系,通过因式分解、 配方等得出边的相应关系,从而判断三角形的形状;
2.利用正弦定理把已知条件转化为内角的三角函数间的关系,通过三角函数恒等变形得出内角的关系,从而判断出三角形的形状,此时要注意应用A+B+C=π这个结论.
注意:在两种解法的等式变形中,一般两边不要约去公因式,应移项提取公因式,以免漏解.
知识归纳
利用正弦定理判断三角形形状的两种方法:
例6:如图所示,在?ABC中,已知 的角分线AD与边BC相交于点D,求证:
证明:如图,设
则由题意可知
在?ABD和?ADC中,分别应用正弦定理,可得
两式相除即可得
内角平分线定理
一题多解:本题也可用面积公式或平面几何知识证明!
D
A
B
C
β
β
α
π–α
1.正弦定理:
正弦定理常用变形:
2.三角形面积公式:
3.正弦定理的应用范围
(1)已知两角和任一边,求其他两边和其余一角.
(2)已知两边和其中一边的对角,求另一边和其余两角.
本节课你学到了哪些知识?
