2.1.1 平均变化率 课件(共17张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2
文档属性
| 名称 | 2.1.1 平均变化率 课件(共17张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2 |  | |
| 格式 | pptx | ||
| 文件大小 | 641.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:25:04 | ||
图片预览




文档简介
(共17张PPT)
2.1.1 平均变化率
第二章 导数及其应用
1.理解函数平均变化率的概念.
2.掌握函数平均变化率的求法.
世界上的变化无处不在,人们经常关心变化的快慢问题.如何刻画事物变化的快慢呢?
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
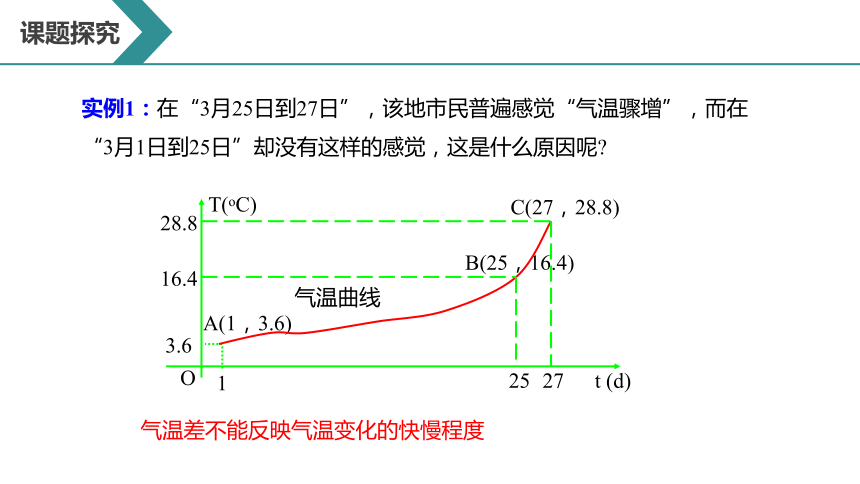
实例1:在“3月25日到27日”,该地市民普遍感觉“气温骤增”,而在“3月1日到25日”却没有这样的感觉,这是什么原因呢
气温差不能反映气温变化的快慢程度
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
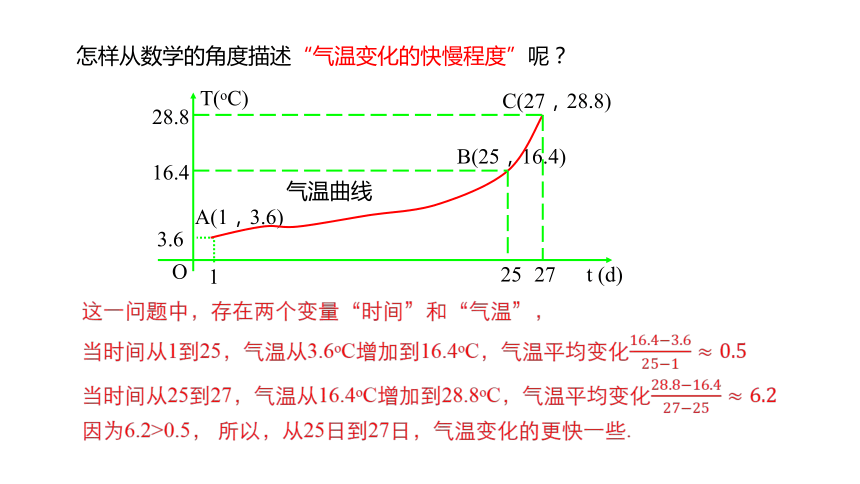
怎样从数学的角度描述“气温变化的快慢程度”呢?
这一问题中,存在两个变量“时间”和“气温”,
当时间从1到25,气温从3.6oC增加到16.4oC,气温平均变化
当时间从25到27,气温从16.4oC增加到28.8oC,气温平均变化
因为6.2>0.5, 所以,从25日到27日,气温变化的更快一些.
实例2:回忆吹气球的过程,随着气球内空气容量的增加,气球半径增长的快慢相同吗
假设每次吹入气球内的空气容量是相等的,如何从数学的角度解释“随着气球内空气容量的增加,气球半径增长的越来越慢”这一现象呢?
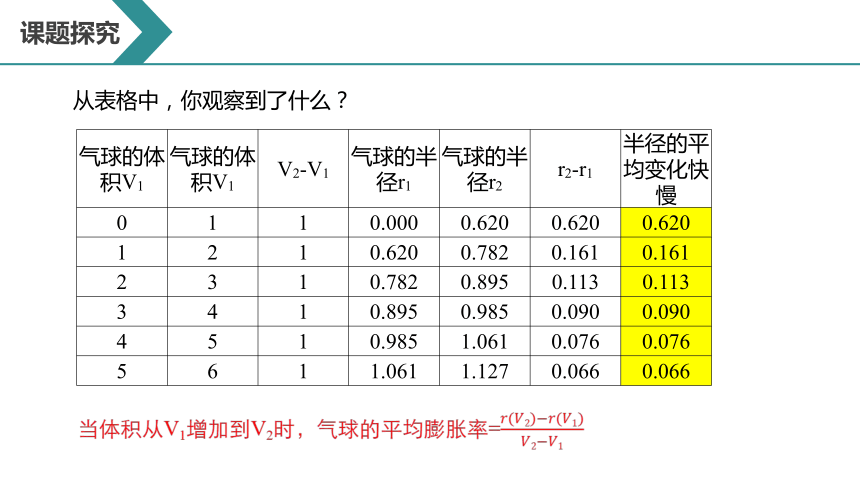
从表格中,你观察到了什么?
气球的体积V1 气球的体积V1 V2-V1 气球的半径r1 气球的半径r2 r2-r1 半径的平均变化快慢
0 1 1 0.000 0.620 0.620 0.620
1 2 1 0.620 0.782 0.161 0.161
2 3 1 0.782 0.895 0.113 0.113
3 4 1 0.895 0.985 0.090 0.090
4 5 1 0.985 1.061 0.076 0.076
5 6 1 1.061 1.127 0.066 0.066
当体积从V1增加到V2时,气球的平均膨胀率=
思考:前面两个生活实例有什么相同的地方?尝试归纳出分析此类问题的一般方法.
概念讲解
平均变化率=
对一般的函数y=f(x)来说,当自变量x从x1变为x2时,函数值从f(x1)变为f(x2), 它在区间[x1, x2]的
通常我们把自变量的变化x2-x1称作自变量x的改变量,记作△x,函数值的变化f(x2)-f(x1)称作函数值y的改变量,记作△y.这样,函数的平均变化率就可以表示为函数值的改变量与自变量的改变量之比,即 用它来刻画函数值在区间[x1, x2]上变化的快慢.
函数平均变化率的几何意义:
如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)). 事实上,
问题:在平均变化率中, Δx, Δy, 是否可以等于0?当平均变化率等于0时,是否说明函数在该区间上一定为常数?
分析:Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0.
当平均变化率等于0时,并不说明函数在该区间上一定为常数.
例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数.
【例1】已知函数f (x)=3x2+5,求f (x):
(1)从0.1到0.2的平均变化率; (2)在区间[x0,x0+Δx]上的平均变化率.
解:(1)因为f(x)=3x2+5,所以从0.1到0.2的平均变化率为
(2)因为+ )2 =6+3()2,
所以函数在区间[,+ ]上的平均变化率为
+3
归纳总结
“三步法”求平均变化率
(1)计算函数值的改变量.
(2)计算自变量的改变量.
(3)得平均变化率
【例2】求函数在到之间的平均变化率,并求当, 时该函数的平均变化率.
解:当自变量从变化到时,函数的平均变化率为
当, 时,平均变化率的值为
根据今天所学,回答下列问题:
1.什么是函数的平均变化率?
2.求函数的平均变化率的步骤.
1.设函数y=f (x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为( )
A. 2.1 B. 1.1 C.2 D.0
2.函数f (x)=x2-x在区间[-2,t]上的平均变化率是2,则t=________.
A
5
3.已知函数的图象上的一点及临近一点
则=( )
A . B. C. D.
4.函数f(x)=8x-6在[m,n]上的平均变化率为 .
D
8
2.1.1 平均变化率
第二章 导数及其应用
1.理解函数平均变化率的概念.
2.掌握函数平均变化率的求法.
世界上的变化无处不在,人们经常关心变化的快慢问题.如何刻画事物变化的快慢呢?
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
实例1:在“3月25日到27日”,该地市民普遍感觉“气温骤增”,而在“3月1日到25日”却没有这样的感觉,这是什么原因呢
气温差不能反映气温变化的快慢程度
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
怎样从数学的角度描述“气温变化的快慢程度”呢?
这一问题中,存在两个变量“时间”和“气温”,
当时间从1到25,气温从3.6oC增加到16.4oC,气温平均变化
当时间从25到27,气温从16.4oC增加到28.8oC,气温平均变化
因为6.2>0.5, 所以,从25日到27日,气温变化的更快一些.
实例2:回忆吹气球的过程,随着气球内空气容量的增加,气球半径增长的快慢相同吗
假设每次吹入气球内的空气容量是相等的,如何从数学的角度解释“随着气球内空气容量的增加,气球半径增长的越来越慢”这一现象呢?
从表格中,你观察到了什么?
气球的体积V1 气球的体积V1 V2-V1 气球的半径r1 气球的半径r2 r2-r1 半径的平均变化快慢
0 1 1 0.000 0.620 0.620 0.620
1 2 1 0.620 0.782 0.161 0.161
2 3 1 0.782 0.895 0.113 0.113
3 4 1 0.895 0.985 0.090 0.090
4 5 1 0.985 1.061 0.076 0.076
5 6 1 1.061 1.127 0.066 0.066
当体积从V1增加到V2时,气球的平均膨胀率=
思考:前面两个生活实例有什么相同的地方?尝试归纳出分析此类问题的一般方法.
概念讲解
平均变化率=
对一般的函数y=f(x)来说,当自变量x从x1变为x2时,函数值从f(x1)变为f(x2), 它在区间[x1, x2]的
通常我们把自变量的变化x2-x1称作自变量x的改变量,记作△x,函数值的变化f(x2)-f(x1)称作函数值y的改变量,记作△y.这样,函数的平均变化率就可以表示为函数值的改变量与自变量的改变量之比,即 用它来刻画函数值在区间[x1, x2]上变化的快慢.
函数平均变化率的几何意义:
如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)). 事实上,
问题:在平均变化率中, Δx, Δy, 是否可以等于0?当平均变化率等于0时,是否说明函数在该区间上一定为常数?
分析:Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0.
当平均变化率等于0时,并不说明函数在该区间上一定为常数.
例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数.
【例1】已知函数f (x)=3x2+5,求f (x):
(1)从0.1到0.2的平均变化率; (2)在区间[x0,x0+Δx]上的平均变化率.
解:(1)因为f(x)=3x2+5,所以从0.1到0.2的平均变化率为
(2)因为+ )2 =6+3()2,
所以函数在区间[,+ ]上的平均变化率为
+3
归纳总结
“三步法”求平均变化率
(1)计算函数值的改变量.
(2)计算自变量的改变量.
(3)得平均变化率
【例2】求函数在到之间的平均变化率,并求当, 时该函数的平均变化率.
解:当自变量从变化到时,函数的平均变化率为
当, 时,平均变化率的值为
根据今天所学,回答下列问题:
1.什么是函数的平均变化率?
2.求函数的平均变化率的步骤.
1.设函数y=f (x)=x2-1,当自变量x由1变为1.1时,函数的平均变化率为( )
A. 2.1 B. 1.1 C.2 D.0
2.函数f (x)=x2-x在区间[-2,t]上的平均变化率是2,则t=________.
A
5
3.已知函数的图象上的一点及临近一点
则=( )
A . B. C. D.
4.函数f(x)=8x-6在[m,n]上的平均变化率为 .
D
8
同课章节目录
