2.2.2 导数的几何意义 课件 (共15张PPT)2024-2025学年高二数学北师版(2019)选择性必修2
文档属性
| 名称 | 2.2.2 导数的几何意义 课件 (共15张PPT)2024-2025学年高二数学北师版(2019)选择性必修2 |  | |
| 格式 | pptx | ||
| 文件大小 | 650.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:31:52 | ||
图片预览




文档简介
2.2.2 导数的几何意义
第二章 导数及其应用
1.根据导数的几何意义,会求曲线上某点处的切线方程.
平均变化率的几何意义
【问题1】设函数y=f (x)的图象如图,点 ,点 ,
则 在 上的平均变化率为
结合直线斜率的定义可知:函数在点P0到点P之间的平均变化率即为割线P0P的斜率.
它表示什么?
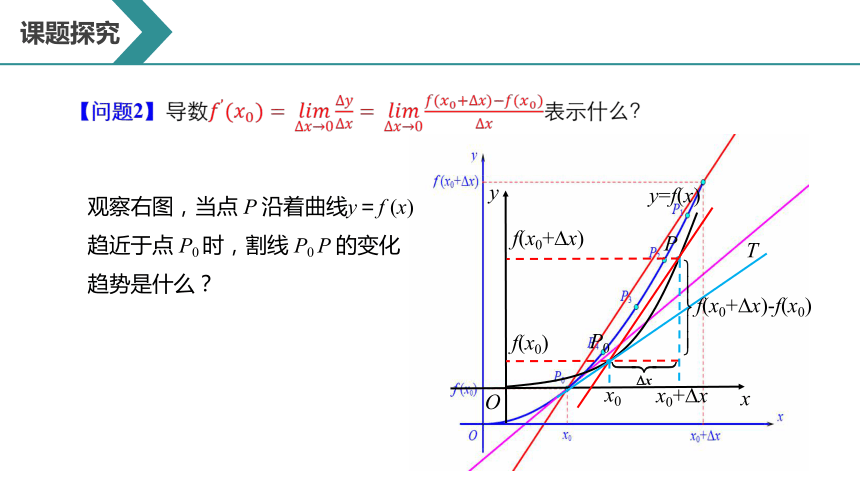
【问题2】导数????’(????0)=?????????????????→0??????????=?????????????????→0????(????0+?????)?????(????0)?????表示什么?
?
x
y
x0
x0+?x
f(x0)
f(x0+?x)
y=f(x)
O
P
?
P0
T
?
f(x0+?x)-f(x0)
观察右图,当点 P 沿着曲线y=f (x)趋近于点 P0 时,割线 P0 P 的变化趋势是什么?
我们发现,当点P(x, f (x))沿着曲线y=f (x)无限趋近于点P0(x0, f (x0))时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
x
y
O
y=f (x)
f (x0)
x0
T
切线的定义:
P0
P
在曲线y=f (x)上任取一点P(x, f (x))
此切线定义与初中学过的圆的切线定义有何不同 ?
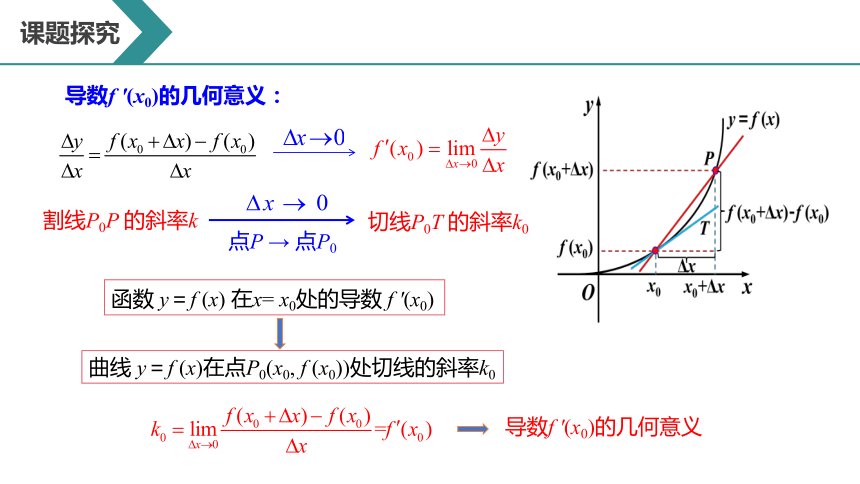
导数f ′(x0)的几何意义:
割线P0P 的斜率k
切线P0T 的斜率k0
点P → 点P0
函数 y=f (x) 在x= x0处的导数 f ′(x0)
曲线 y=f (x)在点P0(x0, f (x0))处切线的斜率k0
导数f ′(x0)的几何意义
P0
T
P0
T
P0
T
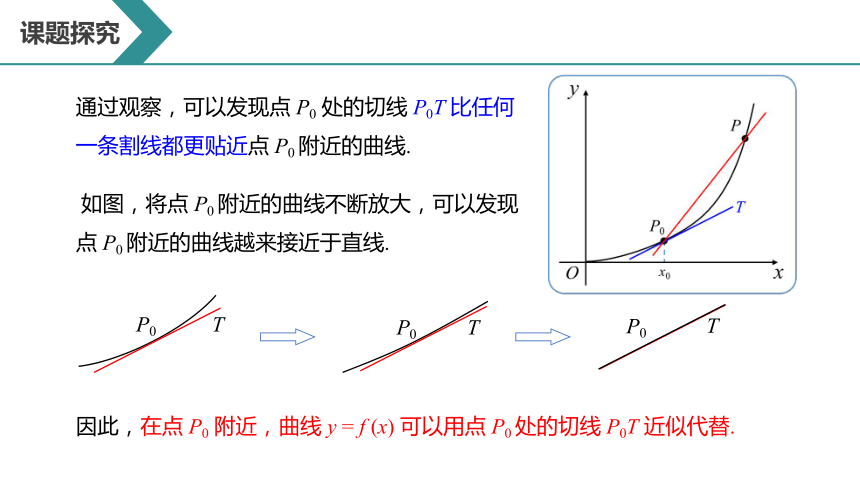
通过观察,可以发现点 P0 处的切线 P0T 比任何一条割线都更贴近点 P0 附近的曲线.
如图,将点 P0 附近的曲线不断放大,可以发现点 P0 附近的曲线越来接近于直线.
因此,在点 P0 附近,曲线 y = f (x) 可以用点 P0 处的切线 P0T 近似代替.
P
x
y
O
T
即
思考:你能求出曲线y=f (x)在点M(x0, f (x0))处的切线方程是什么吗?
【例1】已知函数y=x2及自变量x0=-2.
(1)分别对△x=l,0.5,0.1求y=x2在区间[x0,x0+△x]上的平均变化率,并画出过点(x0,f(x0))的相应割线;
(2)求函数y=x2在x0处的导数,并画岀曲线y=x2在点(x0,f(x0))处的切线.
解:当△x=l,0.5,0.1时,区间[x0,x0+△x]相应为[-2,-1],[-2,-1.5],[-2,-1.9],y=x2在这些区间的平均变化率分别为
令△x趋于0,可知函数y=x2在x0=-2处的导数为-4.
如图,其相应割线分别是经过点(-2,4)和点(-1,1)的直线l1,经过点(-2,4)和点(-1.5,2.25)的直线l2,经过点(-2,4)和点(-1.9,3.61)的直线l3.
(2)函数y=x2在区间[x0,x0+△x]上的平均变化率为
因此,曲线y=x2在点(-2,4)处的切线为经过点(-2,4),斜率为-4的直线l,如图.
【例2】已知函数????(????)=1????,求曲线y=????(????)在(2,????2)处的切线方程.
?
解:因为????′2 =lim?????→0????2+??????????(2)?????
=lim?????→012+??????12?????=lim?????→0?12(2+?????)=?14,
又因为????(2)=12,
所以切线的方程为 y?12=?14(?????2),
即????+4?????4=0.
?
切点坐标(2, 12)
?
斜率为?14
?
归纳总结
求曲线在某点处的切线方程的步骤
根据今天所学,回答下列问题:
1.导数的几何意义是什么?
2.如何求函数在某点处的切线的方程?
1.如图,直线l是曲线y=f(x)在x=4处的切线,
则f ′(x0)=( )
A.0.5 B.3 C.4 D.5
2.曲线y=-2x2 +1在点P(1,-1)处的切线方程为 .
A
4x+y-3=0
3.已知函数f(x)的图象如图所示,则下列不等关系中正确的是( )
A.0 B.0 C.0 D.0C
第二章 导数及其应用
1.根据导数的几何意义,会求曲线上某点处的切线方程.
平均变化率的几何意义
【问题1】设函数y=f (x)的图象如图,点 ,点 ,
则 在 上的平均变化率为
结合直线斜率的定义可知:函数在点P0到点P之间的平均变化率即为割线P0P的斜率.
它表示什么?
【问题2】导数????’(????0)=?????????????????→0??????????=?????????????????→0????(????0+?????)?????(????0)?????表示什么?
?
x
y
x0
x0+?x
f(x0)
f(x0+?x)
y=f(x)
O
P
?
P0
T
?
f(x0+?x)-f(x0)
观察右图,当点 P 沿着曲线y=f (x)趋近于点 P0 时,割线 P0 P 的变化趋势是什么?
我们发现,当点P(x, f (x))沿着曲线y=f (x)无限趋近于点P0(x0, f (x0))时,割线P0P无限趋近于一个确定的位置,这个确定的位置的直线P0T 称为曲线y=f (x)在点 P0 处的切线.
x
y
O
y=f (x)
f (x0)
x0
T
切线的定义:
P0
P
在曲线y=f (x)上任取一点P(x, f (x))
此切线定义与初中学过的圆的切线定义有何不同 ?
导数f ′(x0)的几何意义:
割线P0P 的斜率k
切线P0T 的斜率k0
点P → 点P0
函数 y=f (x) 在x= x0处的导数 f ′(x0)
曲线 y=f (x)在点P0(x0, f (x0))处切线的斜率k0
导数f ′(x0)的几何意义
P0
T
P0
T
P0
T
通过观察,可以发现点 P0 处的切线 P0T 比任何一条割线都更贴近点 P0 附近的曲线.
如图,将点 P0 附近的曲线不断放大,可以发现点 P0 附近的曲线越来接近于直线.
因此,在点 P0 附近,曲线 y = f (x) 可以用点 P0 处的切线 P0T 近似代替.
P
x
y
O
T
即
思考:你能求出曲线y=f (x)在点M(x0, f (x0))处的切线方程是什么吗?
【例1】已知函数y=x2及自变量x0=-2.
(1)分别对△x=l,0.5,0.1求y=x2在区间[x0,x0+△x]上的平均变化率,并画出过点(x0,f(x0))的相应割线;
(2)求函数y=x2在x0处的导数,并画岀曲线y=x2在点(x0,f(x0))处的切线.
解:当△x=l,0.5,0.1时,区间[x0,x0+△x]相应为[-2,-1],[-2,-1.5],[-2,-1.9],y=x2在这些区间的平均变化率分别为
令△x趋于0,可知函数y=x2在x0=-2处的导数为-4.
如图,其相应割线分别是经过点(-2,4)和点(-1,1)的直线l1,经过点(-2,4)和点(-1.5,2.25)的直线l2,经过点(-2,4)和点(-1.9,3.61)的直线l3.
(2)函数y=x2在区间[x0,x0+△x]上的平均变化率为
因此,曲线y=x2在点(-2,4)处的切线为经过点(-2,4),斜率为-4的直线l,如图.
【例2】已知函数????(????)=1????,求曲线y=????(????)在(2,????2)处的切线方程.
?
解:因为????′2 =lim?????→0????2+??????????(2)?????
=lim?????→012+??????12?????=lim?????→0?12(2+?????)=?14,
又因为????(2)=12,
所以切线的方程为 y?12=?14(?????2),
即????+4?????4=0.
?
切点坐标(2, 12)
?
斜率为?14
?
归纳总结
求曲线在某点处的切线方程的步骤
根据今天所学,回答下列问题:
1.导数的几何意义是什么?
2.如何求函数在某点处的切线的方程?
1.如图,直线l是曲线y=f(x)在x=4处的切线,
则f ′(x0)=( )
A.0.5 B.3 C.4 D.5
2.曲线y=-2x2 +1在点P(1,-1)处的切线方程为 .
A
4x+y-3=0
3.已知函数f(x)的图象如图所示,则下列不等关系中正确的是( )
A.0
同课章节目录
