2.6.3 函数的最值 课件(共17张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2
文档属性
| 名称 | 2.6.3 函数的最值 课件(共17张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:50:23 | ||
图片预览




文档简介
— 第二章 导数及其应用 —
2.6.3 函数的最值
1.理解极值与最值的区别和联系;
2.掌握求函数最值的方法.
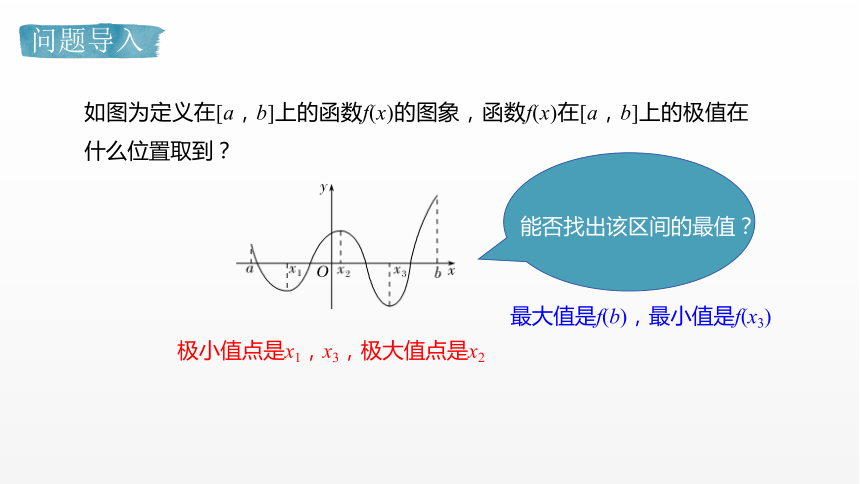
如图为定义在[a,b]上的函数f(x)的图象,函数f(x)在[a,b]上的极值在什么位置取到?
极小值点是x1,x3,极大值点是x2
能否找出该区间的最值?
最大值是f(b),最小值是f(x3)
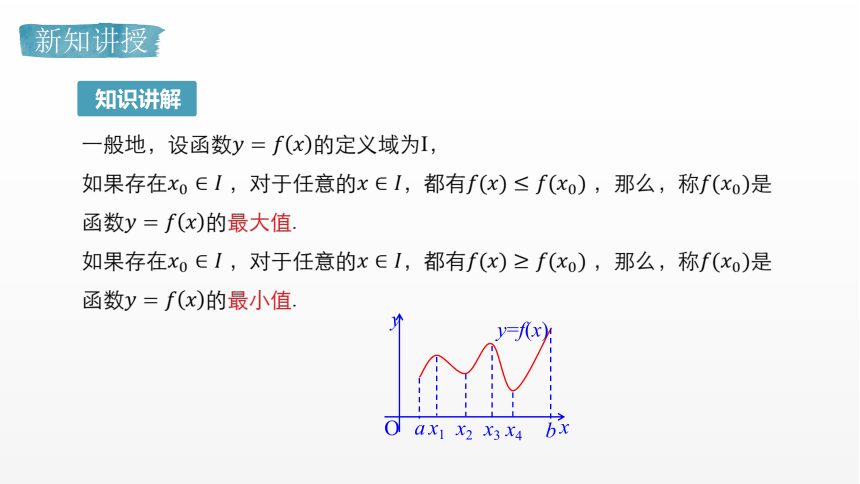
一般地,设函数????=????????的定义域为I,
如果存在????0∈???? ,对于任意的????∈????,都有????(????)≤????(????0) ,那么,称????(????0)是函数????=????????的最大值.
如果存在????0∈???? ,对于任意的????∈????,都有????(????)≥????(????0) ,那么,称????(????0)是函数????=????????的最小值.
?
知识讲解
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
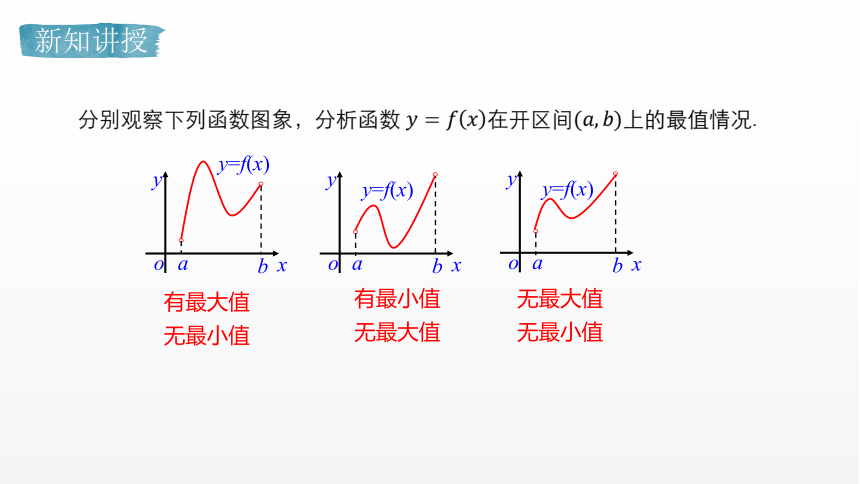
分别观察下列函数图象,分析函数 ????=????????在开区间(????,????)上的最值情况.
?
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
有最大值
无最小值
有最小值
无最大值
无最大值
无最小值
一般地,如果函数 ????=????????在闭区间[????,????]上的图象是一条连续不断的曲线,那么它在[????,????]上必有最大值与最小值.
?
o
x
y
a
b
y=f(x)
归纳总结
观察函数????=????????,????∈[?3,2]的图像,回忆函数最值的定义,回答下列问题:
思考1:图中所示函数的最值点与最值分别是多少?
?
x
y
y = f (x)
?3
?
2
?
O
最大值点为2,最大值为3;
最小值点为0,最小值为-3.
最大值
最小值
思考2:图中所示函数的极值点与极值分别是多少?
极大值点为-2,极大值为2;
极小值点为0,极小值为-3.
讨论:一般的函数的最值与函数的极值有什么关系?怎样求可导函数的最值.
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
① 一般地,如果函数????=????(????)的定义域内为(????,????)且存在最值,函数????=????(????)在(????,????)内可导,则函数的最值点一定是某个极值点;
②如果函数????=????(????)的定义域为[????,????]且存在最值,函数????=????(????)在(????,????)内可导,那么函数的最值点要么是区间端点????或????,要么是极值点.
?
利用导数求出区间内的极值,并与区间端点处函数值比较,即可确定.
判断:1.函数的最大值不一定是函数的极大值.( )
2.函数f(x)在区间[a,b]上的最大值与最小值一定在区间端点处取得.( )
3.有极值的函数一定有最值,有最值的函数不一定有极值.( )
4.函数f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上一定有最值,但不一定有极值.( )
√
×
×
√
也可能在极值点处取到.
有极值的函数不一定有最值,如图所示,导函数f(x)有极值,但没有最值.
例1 已知函数f(x)=1?????????+ln x,求f(x)在[12,2]的最值.
?
例1 已知函数f(x)=1?????????+ln x,求f(x)在[12,2]的最值.
?
例2 已知????(????)=3????3?9????,????∈?2,3,求????(????)在定义域的最值.
?
解:因为f ′(x)=9x2-9=9(x+1)(x-1),
所以令f ′(x)=0得x=-1或x=1.
则当x变化时,f ′(x),f (x)变化状态如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} ????
-2
(-2,-1)
-1
(-1,1)
1
(1,3)
3
?????′(????)
?
+
0
-
0
+
?
?????(????)
-6
↗
6
↘
-6
↗
54
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
(-2,-1)
-1
(-1,1)
1
(1,3)
3
?
+
0
-
0
+
?
-6
↗
6
↘
-6
↗
54
由表可知极值f(-1)=6,f(1)=-6,区间端点函数值f(-2)=-6,f(3)= 54(x= 3不可取),
经比较最小值为-6,无最大值.
例3 已知2xln x≥-x2+ax-3对一切x∈(0,+∞)恒成立,求a的取值范围.
解:由2xln x≥-x2+ax-3(x>0)得a≤2ln x+x+3????(x>0).
设h(x)=2ln x+3????+x(x>0),则h'(x)=(????+3)(?????1)????2,
当x∈(0,1)时,h'(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h'(x)>0,h(x)单调递增.
∴h(x)min=h(1)=4.
∴a≤h(x)min=4.
即a的取值范围是(-∞,4].
?
恒成立问题常利用分离参数法,转化为求函数最值问题求解,一般思路为
方法归纳
1.如图是导函数y=f?′(x)的图象,最大值点一定不是( )
B
A.x1?? B.x2??? C.x3?? D.x4
2.函数y=x-sin x,x∈π2,π的最大值是( )
A.π-1 B.π2-1 C.π D.π+1
3.函数f(x)=x3-3x(|x|<1)( )
A.有最值,但无极值 B.有最值,也有极值
C.既无最值,也无极值 D.无最值,但有极值
4.已知函数f(x)=ex-x+a,若f(x)>0恒成立,则实数a的取值范围是( )
A.(-1,+∞) B.(-∞,-1) C.[-1,+∞) D.(-∞,-1]
?
C
C
A
回顾:结合本课内容,回答下列问题?
1. 函数的极值与最值有什么关系?
2. 如何求一个函数的最值?
2.6.3 函数的最值
1.理解极值与最值的区别和联系;
2.掌握求函数最值的方法.
如图为定义在[a,b]上的函数f(x)的图象,函数f(x)在[a,b]上的极值在什么位置取到?
极小值点是x1,x3,极大值点是x2
能否找出该区间的最值?
最大值是f(b),最小值是f(x3)
一般地,设函数????=????????的定义域为I,
如果存在????0∈???? ,对于任意的????∈????,都有????(????)≤????(????0) ,那么,称????(????0)是函数????=????????的最大值.
如果存在????0∈???? ,对于任意的????∈????,都有????(????)≥????(????0) ,那么,称????(????0)是函数????=????????的最小值.
?
知识讲解
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
分别观察下列函数图象,分析函数 ????=????????在开区间(????,????)上的最值情况.
?
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
o
x
y
a
b
y=f(x)
有最大值
无最小值
有最小值
无最大值
无最大值
无最小值
一般地,如果函数 ????=????????在闭区间[????,????]上的图象是一条连续不断的曲线,那么它在[????,????]上必有最大值与最小值.
?
o
x
y
a
b
y=f(x)
归纳总结
观察函数????=????????,????∈[?3,2]的图像,回忆函数最值的定义,回答下列问题:
思考1:图中所示函数的最值点与最值分别是多少?
?
x
y
y = f (x)
?3
?
2
?
O
最大值点为2,最大值为3;
最小值点为0,最小值为-3.
最大值
最小值
思考2:图中所示函数的极值点与极值分别是多少?
极大值点为-2,极大值为2;
极小值点为0,极小值为-3.
讨论:一般的函数的最值与函数的极值有什么关系?怎样求可导函数的最值.
y
x
O
a
b
y=f(x)
x1
x2
x3
x4
① 一般地,如果函数????=????(????)的定义域内为(????,????)且存在最值,函数????=????(????)在(????,????)内可导,则函数的最值点一定是某个极值点;
②如果函数????=????(????)的定义域为[????,????]且存在最值,函数????=????(????)在(????,????)内可导,那么函数的最值点要么是区间端点????或????,要么是极值点.
?
利用导数求出区间内的极值,并与区间端点处函数值比较,即可确定.
判断:1.函数的最大值不一定是函数的极大值.( )
2.函数f(x)在区间[a,b]上的最大值与最小值一定在区间端点处取得.( )
3.有极值的函数一定有最值,有最值的函数不一定有极值.( )
4.函数f(x)在区间[a,b]上连续,则f(x)在区间[a,b]上一定有最值,但不一定有极值.( )
√
×
×
√
也可能在极值点处取到.
有极值的函数不一定有最值,如图所示,导函数f(x)有极值,但没有最值.
例1 已知函数f(x)=1?????????+ln x,求f(x)在[12,2]的最值.
?
例1 已知函数f(x)=1?????????+ln x,求f(x)在[12,2]的最值.
?
例2 已知????(????)=3????3?9????,????∈?2,3,求????(????)在定义域的最值.
?
解:因为f ′(x)=9x2-9=9(x+1)(x-1),
所以令f ′(x)=0得x=-1或x=1.
则当x变化时,f ′(x),f (x)变化状态如下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} ????
-2
(-2,-1)
-1
(-1,1)
1
(1,3)
3
?????′(????)
?
+
0
-
0
+
?
?????(????)
-6
↗
6
↘
-6
↗
54
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
-2
(-2,-1)
-1
(-1,1)
1
(1,3)
3
?
+
0
-
0
+
?
-6
↗
6
↘
-6
↗
54
由表可知极值f(-1)=6,f(1)=-6,区间端点函数值f(-2)=-6,f(3)= 54(x= 3不可取),
经比较最小值为-6,无最大值.
例3 已知2xln x≥-x2+ax-3对一切x∈(0,+∞)恒成立,求a的取值范围.
解:由2xln x≥-x2+ax-3(x>0)得a≤2ln x+x+3????(x>0).
设h(x)=2ln x+3????+x(x>0),则h'(x)=(????+3)(?????1)????2,
当x∈(0,1)时,h'(x)<0,h(x)单调递减;
当x∈(1,+∞)时,h'(x)>0,h(x)单调递增.
∴h(x)min=h(1)=4.
∴a≤h(x)min=4.
即a的取值范围是(-∞,4].
?
恒成立问题常利用分离参数法,转化为求函数最值问题求解,一般思路为
方法归纳
1.如图是导函数y=f?′(x)的图象,最大值点一定不是( )
B
A.x1?? B.x2??? C.x3?? D.x4
2.函数y=x-sin x,x∈π2,π的最大值是( )
A.π-1 B.π2-1 C.π D.π+1
3.函数f(x)=x3-3x(|x|<1)( )
A.有最值,但无极值 B.有最值,也有极值
C.既无最值,也无极值 D.无最值,但有极值
4.已知函数f(x)=ex-x+a,若f(x)>0恒成立,则实数a的取值范围是( )
A.(-1,+∞) B.(-∞,-1) C.[-1,+∞) D.(-∞,-1]
?
C
C
A
回顾:结合本课内容,回答下列问题?
1. 函数的极值与最值有什么关系?
2. 如何求一个函数的最值?
同课章节目录
