2.7.1 实际问题中导数的意义&2.7.2 实际问题中的最值问题 课件(共16张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2
文档属性
| 名称 | 2.7.1 实际问题中导数的意义&2.7.2 实际问题中的最值问题 课件(共16张PPT) 2024-2025学年高二数学北师版(2019)选择性必修2 |  | |
| 格式 | pptx | ||
| 文件大小 | 878.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:51:33 | ||
图片预览






文档简介
2.7.1 实际问题中导数的意义
&2.7.2 实际问题中的最值问题
北师大版(2019)选择性必修二
1.了解实际问题中导数的意义.
2.能利用导数知识解决实际生活中的最优化问题.
例1 物体作自由落体运动,其方程为s(t)=12gt2(其中位移单位:m,时间单位:s,g=9.8 m/s2).
(1)计算当t从2 s变到4 s时位移s关于时间t的平均变化率,并解释它的意义;
(2)求s′(2),并解释它的意义.
?
解:(1)当t从2 s变到4 s时,位移s从s(2)变到s(4),
此时,位移s关于时间t的平均变化率为
它表示物体从2 s到4 s这段时间平均每秒下落29.4 m.
例1 物体作自由落体运动,其方程为s(t)=12gt2(其中位移单位:m,时间单位:s,g=9.8 m/s2).
(2)求s′(2),并解释它的意义.
?
(2)∵s′(t)=gt,∴s′(2)=2g=19.6(m/s).
它表示物体在t=2 s时的瞬时速度为19.6 m/s.
归纳总结
在物理学中:
(1)瞬时速度:物体在某一时刻的速度称为瞬时速度,它是位移s关于时间t的导数;速度v关于时间t的导数是加速度.
(2)功与功率:通常称力在单位时间内做的功为功率,它是功W关于时间t的导数.
(3)线密度:单位长度的物质质量称为线密度,它是质量关于长度的导数.
解:当x从10件提高到20件时,
总成本C从C(10)=2 675元变到C(20)=3 350元.
其表示日产量从10件提高到20件时平均每件产品的总成本的改变量.
例2 某机械厂生产某种机器配件的最大生产能力为每日100件,假设日产品
的总成本C(元)与日产量x(件)的函数关系为C(x)=14x2+60x+2 050.求当日产量
由10件提高到20件时,总成本的平均改变量,并说明其实际意义.
?
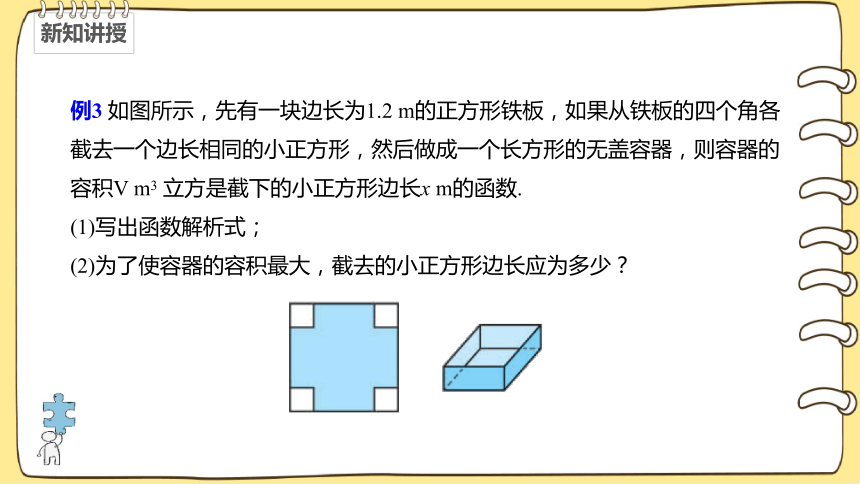
例3 如图所示,先有一块边长为1.2 m的正方形铁板,如果从铁板的四个角各截去一个边长相同的小正方形,然后做成一个长方形的无盖容器,则容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
????
?
1.2?2????
?
????
?
1.2?2????
?
1.2?2????
?
例3 容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
解:(1)根据题意可知,容器底面的边长为(1.2?2????)m,高为?????m ,于是
????=(1.2?2????)2????.
?
又因为显然????的长度必须小于原有正方形铁板的一半,因此0所以????=(1.2?2????)2????,0?
注意:函数的单调区间应联系问题的实际意义确定.
????
?
1.2?2????
?
????
?
1.2?2????
?
1.2?2????
?
例3 容器的容积V m3 立方是截下的小正方形边长x m的函数.
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
(2)由题意有
????′= 21.2?2????×?2????+(1.2?2????)2
=12(?????0.6)(?????0.2).
令????′>0,可解得????<0.2.
?
因此可知????在(0,?0.2]上递增,在[0.2,?0.6)上递减,
故????在????=0.2时取得极大值,而且在此时取得最大值.
即截去的正方形边长为0.2m时,容器的容积最大.
?
利用导数解决实际问题的一般步骤:
(1)抽象出实际问题的数学模型,列出函数解析式????=?????(????),标明自变量的取值范围;
(2)求导数 ????′(????)?并解方程????′????=0,即求出函数可能的极值点;
(3)比较函数????(????)在区间端点的函数值与极值的大小,得出函数最值;
(4)根据实际问题的意义,给出相应答案.
?
归纳总结
例4 已知某种工艺品总成本C元是产量Q件的函数,且
????=10????2+200????+1000,1≤????≤30.
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件产品的平均成本最低?最低平均成本为多少?
?
解:记平均成本为????????元,则
???????? =???????? =10????2+200????+1000????= 10????+1000????+200.
因为10,可解得????>10.
因此可知????????在[1,10]上递减,在10,30上递增,从而????????在?Q=10时取得极小值,而且在此事取得最小值
???????? = 10×10+100010+200=400.
及当月产量为10万件,是每件产品的平均成本最低最低为400元.
?
1.(多选)下列四个命题是假命题的是( )
A.曲线y=x3在原点处没有切线
B.若函数f(x)=????,则f′(0)=0
C.加速度是动点位移函数s(t)对时间t的导数
D.函数y=x5的导函数的值恒非负
?
ABC
2.一个箱子的容积与底面边长x的关系为V(x)=x260?????2 (0 A.30 B.40 C.50 D.60
?
B
3.已知某厂生产某种商品x(百件)的总成本函数为C(x)=13x3-6x2+29x+15(万元),总收益函数为R(x)=20x-x2(万元),则生产这种商品所获利润的最大值为______万元.
?
66
4.某公司租地建仓库,每月土地占用费y1(单位:万元)与仓库到车站的距离成反比,而每月库存货物的运费y2(单位:万元)与到车站的距离成正比.如果在距离车站10千米处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站 千米处.?
5
&2.7.2 实际问题中的最值问题
北师大版(2019)选择性必修二
1.了解实际问题中导数的意义.
2.能利用导数知识解决实际生活中的最优化问题.
例1 物体作自由落体运动,其方程为s(t)=12gt2(其中位移单位:m,时间单位:s,g=9.8 m/s2).
(1)计算当t从2 s变到4 s时位移s关于时间t的平均变化率,并解释它的意义;
(2)求s′(2),并解释它的意义.
?
解:(1)当t从2 s变到4 s时,位移s从s(2)变到s(4),
此时,位移s关于时间t的平均变化率为
它表示物体从2 s到4 s这段时间平均每秒下落29.4 m.
例1 物体作自由落体运动,其方程为s(t)=12gt2(其中位移单位:m,时间单位:s,g=9.8 m/s2).
(2)求s′(2),并解释它的意义.
?
(2)∵s′(t)=gt,∴s′(2)=2g=19.6(m/s).
它表示物体在t=2 s时的瞬时速度为19.6 m/s.
归纳总结
在物理学中:
(1)瞬时速度:物体在某一时刻的速度称为瞬时速度,它是位移s关于时间t的导数;速度v关于时间t的导数是加速度.
(2)功与功率:通常称力在单位时间内做的功为功率,它是功W关于时间t的导数.
(3)线密度:单位长度的物质质量称为线密度,它是质量关于长度的导数.
解:当x从10件提高到20件时,
总成本C从C(10)=2 675元变到C(20)=3 350元.
其表示日产量从10件提高到20件时平均每件产品的总成本的改变量.
例2 某机械厂生产某种机器配件的最大生产能力为每日100件,假设日产品
的总成本C(元)与日产量x(件)的函数关系为C(x)=14x2+60x+2 050.求当日产量
由10件提高到20件时,总成本的平均改变量,并说明其实际意义.
?
例3 如图所示,先有一块边长为1.2 m的正方形铁板,如果从铁板的四个角各截去一个边长相同的小正方形,然后做成一个长方形的无盖容器,则容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
????
?
1.2?2????
?
????
?
1.2?2????
?
1.2?2????
?
例3 容器的容积V m3 立方是截下的小正方形边长x m的函数.
(1)写出函数解析式;
解:(1)根据题意可知,容器底面的边长为(1.2?2????)m,高为?????m ,于是
????=(1.2?2????)2????.
?
又因为显然????的长度必须小于原有正方形铁板的一半,因此0所以????=(1.2?2????)2????,0?
注意:函数的单调区间应联系问题的实际意义确定.
????
?
1.2?2????
?
????
?
1.2?2????
?
1.2?2????
?
例3 容器的容积V m3 立方是截下的小正方形边长x m的函数.
(2)为了使容器的容积最大,截去的小正方形边长应为多少?
(2)由题意有
????′= 21.2?2????×?2????+(1.2?2????)2
=12(?????0.6)(?????0.2).
令????′>0,可解得????<0.2.
?
因此可知????在(0,?0.2]上递增,在[0.2,?0.6)上递减,
故????在????=0.2时取得极大值,而且在此时取得最大值.
即截去的正方形边长为0.2m时,容器的容积最大.
?
利用导数解决实际问题的一般步骤:
(1)抽象出实际问题的数学模型,列出函数解析式????=?????(????),标明自变量的取值范围;
(2)求导数 ????′(????)?并解方程????′????=0,即求出函数可能的极值点;
(3)比较函数????(????)在区间端点的函数值与极值的大小,得出函数最值;
(4)根据实际问题的意义,给出相应答案.
?
归纳总结
例4 已知某种工艺品总成本C元是产量Q件的函数,且
????=10????2+200????+1000,1≤????≤30.
将Q看成能取区间[1, 30]内的每一个值,求月产量Q为多少时,才能使每件产品的平均成本最低?最低平均成本为多少?
?
解:记平均成本为????????元,则
???????? =???????? =10????2+200????+1000????= 10????+1000????+200.
因为10,可解得????>10.
因此可知????????在[1,10]上递减,在10,30上递增,从而????????在?Q=10时取得极小值,而且在此事取得最小值
???????? = 10×10+100010+200=400.
及当月产量为10万件,是每件产品的平均成本最低最低为400元.
?
1.(多选)下列四个命题是假命题的是( )
A.曲线y=x3在原点处没有切线
B.若函数f(x)=????,则f′(0)=0
C.加速度是动点位移函数s(t)对时间t的导数
D.函数y=x5的导函数的值恒非负
?
ABC
2.一个箱子的容积与底面边长x的关系为V(x)=x260?????2 (0
?
B
3.已知某厂生产某种商品x(百件)的总成本函数为C(x)=13x3-6x2+29x+15(万元),总收益函数为R(x)=20x-x2(万元),则生产这种商品所获利润的最大值为______万元.
?
66
4.某公司租地建仓库,每月土地占用费y1(单位:万元)与仓库到车站的距离成反比,而每月库存货物的运费y2(单位:万元)与到车站的距离成正比.如果在距离车站10千米处建仓库,这两项费用y1和y2分别为2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站 千米处.?
5
同课章节目录
