6.3.2 刻画空间点线面位置关系的公理第一课时三个基本事实 课件(共18张PPT)2024-2025学年高一数学北师版(2019)必修第二册
文档属性
| 名称 | 6.3.2 刻画空间点线面位置关系的公理第一课时三个基本事实 课件(共18张PPT)2024-2025学年高一数学北师版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 917.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
第6章 立体几何初步
3.2 刻画空间点线面位置关系的公理
第一课时 三个基本事实
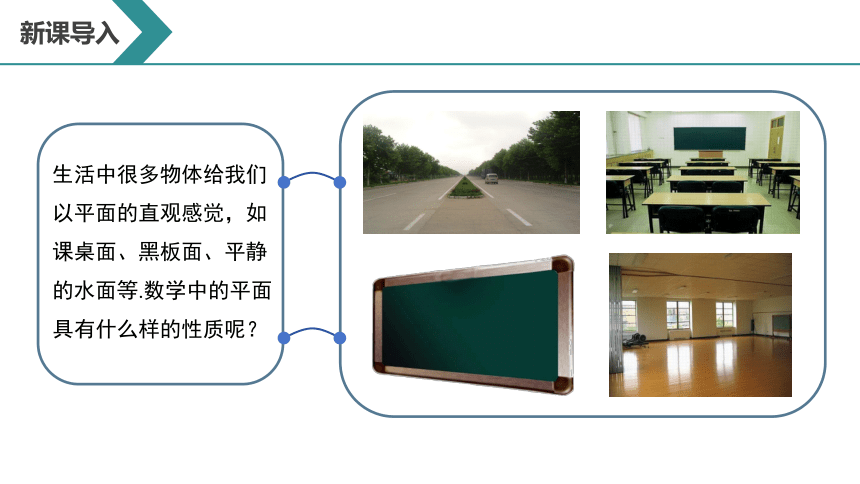
生活中很多物体给我们以平面的直观感觉,如课桌面、黑板面、平静的水面等.数学中的平面具有什么样的性质呢?
平面的基本性质
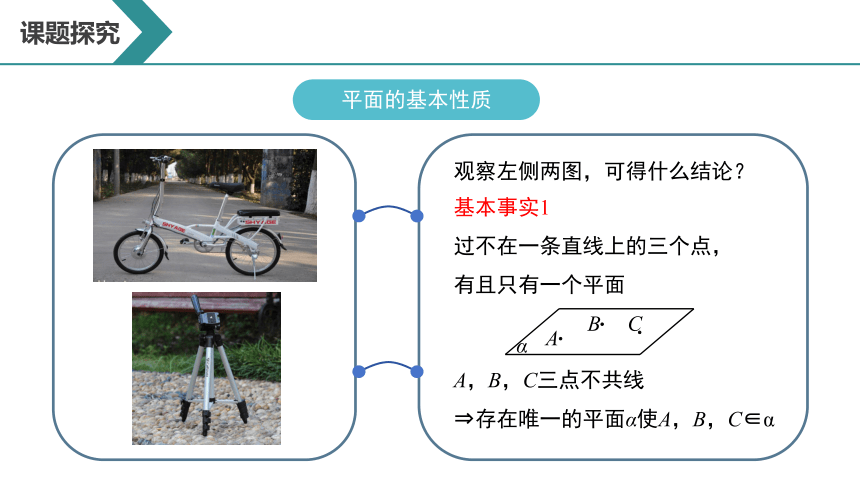
观察左侧两图,可得什么结论?
基本事实1
过不在一条直线上的三个点,
有且只有一个平面
α
A
B
C
A,B,C三点不共线
存在唯一的平面α使A,B,C∈α
平面的基本性质
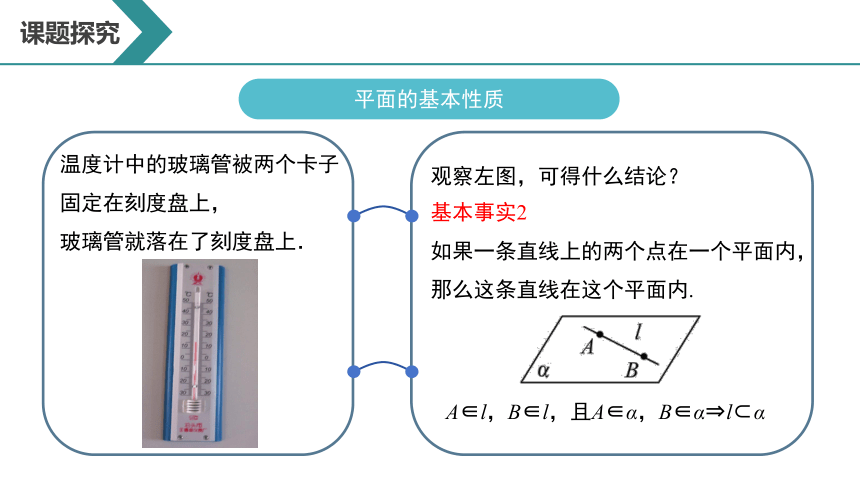
温度计中的玻璃管被两个卡子
固定在刻度盘上,
玻璃管就落在了刻度盘上.
观察左图,可得什么结论?
基本事实2
如果一条直线上的两个点在一个平面内,
那么这条直线在这个平面内.
A∈l,B∈l,且A∈α,B∈α l α
平面的基本性质
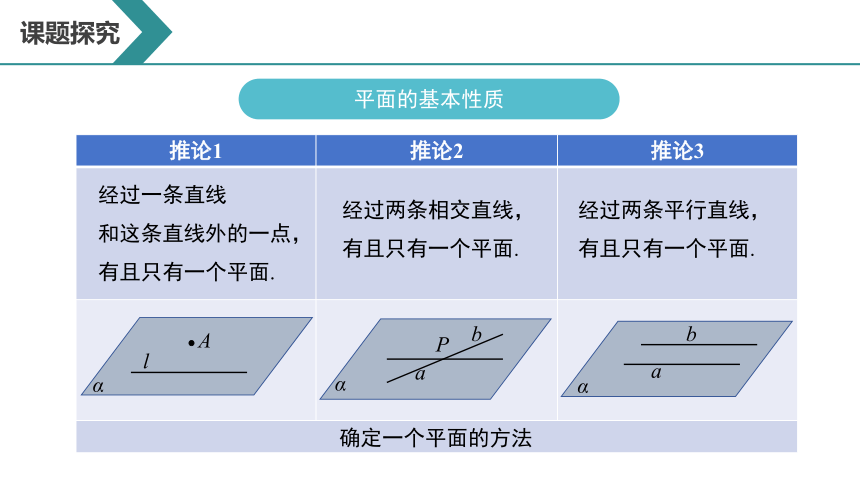
推论1 推论2 推论3
经过一条直线
和这条直线外的一点,
有且只有一个平面.
经过两条平行直线,
有且只有一个平面.
经过两条相交直线,
有且只有一个平面.
l
A
α
a
b
α
b
a
α
P
确定一个平面的方法
平面的基本性质
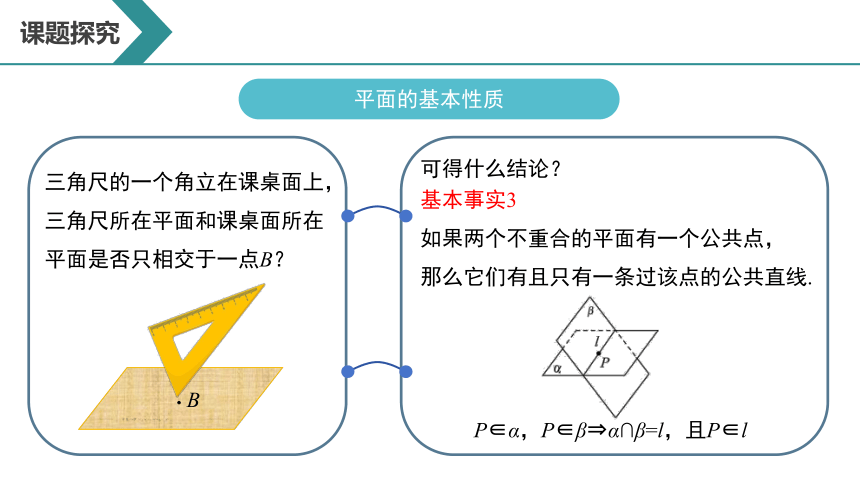
B
三角尺的一个角立在课桌面上,三角尺所在平面和课桌面所在平面是否只相交于一点B?
可得什么结论?
基本事实3
如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
P∈α,P∈β α∩β=l,且P∈l
题型一:图形语言、文字语言、符号语言的相互转换
例1 (1)点P在直线a上,直线a在平面α内可记为
A.P∈a,a α B.P a,a α
C.P a,a∈α D.P∈a,a∈α
解:“∈”表示点在线上以及点在面内,
“ ”表示线在面内,故选A.
例2 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
解:用符号表示:α∩β=l,a∩α=A,a∩β=B,如图.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解:用符号表示:A∈α,B∈α,a∩α=C,C AB,如图.
题型二:点、线共面问题
例2 如图,已知a α,b α,a∩b=A,P∈b,PQ∥a,求证:PQ α.
证明 因为PQ∥a,
所以PQ与a确定一个平面β,所以直线a β,点P∈β.
因为P∈b,b α,
所以P∈α.
又因为a α,P a,所以α与β重合,所以PQ α.
例3 证明:两两相交且不过同一点的三条直线在同一平面内.
解:已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
证明 方法一
因为l1∩l2=A,所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.
又因为l2 α,所以B∈α.
同理可证C∈α.
又因为B∈l3,C∈l3,所以l3 α.
所以直线l1,l2,l3在同一平面内.
方法二
因为l1∩l2=A,所以l1、l2确定一个平面α.
因为l2∩l3=B,所以l2、l3确定一个平面β.
因为A∈l2,l2 α,所以A∈α.
因为A∈l2,l2 β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A、B、C既在平面α内,
又在平面β内.
所以平面α和β重合,
即直线l1,l2,l3在同一平面内.
题型三:证明点共线、线共点问题
例4 如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA
上的点,且直线EH与直线FG交于点O.
求证:B,D,O三点共线.
证明 因为E∈AB,H∈AD,
所以E∈平面ABD,H∈平面ABD.所以EH 平面ABD.
因为EH∩FG=O,所以O∈平面ABD.
同理O∈平面BCD,即O为面ABD与面BCD的公共点,
所以O∈BD,即B,D,O三点共线.
例5 如图,已知平面α,β,且α∩β=l,设梯形ABCD中,AD∥BC,
且AB α,CD β.求证:AB,CD,l共点.
证明 ∵在梯形ABCD中,AD∥BC,
∴AB与CD必交于一点,
设AB交CD于M.
则M∈AB,M∈CD,
又∵AB α,CD β,
∴M∈α,M∈β,
又∵α∩β=l,
∴M∈l,
∴AB,CD,l共点.
1.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为
A.A a,a α,B∈α B.A∈a,a α,B∈α
C.A a,a∈α,B α D.A∈a,a∈α,B∈α
解:点A在直线a上,而直线a在平面α内,点B在平面α内,表示为A∈a,a α,B∈α.
故选B.
2.能确定一个平面的条件是
A.空间三个点 B.一个点和一条直线
C.无数个点 D.两条相交直线
解:A项,三个点可能共线,
B项,点可能在直线上,
C项,无数个点也可能在同一条直线上.
故选D.
3.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是____________.
解:因为P∈AB,AB 平面ABC,所以P∈平面ABC.
又P∈α,平面ABC∩平面α=DE,所以P∈直线DE.
平面
确定平面的条件
基本事实1
线在面内
基本事实2
点共线、线共点
基本事实3
确定平面的条件
三个推论
第6章 立体几何初步
3.2 刻画空间点线面位置关系的公理
第一课时 三个基本事实
生活中很多物体给我们以平面的直观感觉,如课桌面、黑板面、平静的水面等.数学中的平面具有什么样的性质呢?
平面的基本性质
观察左侧两图,可得什么结论?
基本事实1
过不在一条直线上的三个点,
有且只有一个平面
α
A
B
C
A,B,C三点不共线
存在唯一的平面α使A,B,C∈α
平面的基本性质
温度计中的玻璃管被两个卡子
固定在刻度盘上,
玻璃管就落在了刻度盘上.
观察左图,可得什么结论?
基本事实2
如果一条直线上的两个点在一个平面内,
那么这条直线在这个平面内.
A∈l,B∈l,且A∈α,B∈α l α
平面的基本性质
推论1 推论2 推论3
经过一条直线
和这条直线外的一点,
有且只有一个平面.
经过两条平行直线,
有且只有一个平面.
经过两条相交直线,
有且只有一个平面.
l
A
α
a
b
α
b
a
α
P
确定一个平面的方法
平面的基本性质
B
三角尺的一个角立在课桌面上,三角尺所在平面和课桌面所在平面是否只相交于一点B?
可得什么结论?
基本事实3
如果两个不重合的平面有一个公共点,
那么它们有且只有一条过该点的公共直线.
P∈α,P∈β α∩β=l,且P∈l
题型一:图形语言、文字语言、符号语言的相互转换
例1 (1)点P在直线a上,直线a在平面α内可记为
A.P∈a,a α B.P a,a α
C.P a,a∈α D.P∈a,a∈α
解:“∈”表示点在线上以及点在面内,
“ ”表示线在面内,故选A.
例2 用符号表示下列语句,并画出图形.
(1)平面α与β相交于直线l,直线a与α,β分别相交于点A,B;
解:用符号表示:α∩β=l,a∩α=A,a∩β=B,如图.
(2)点A,B在平面α内,直线a与平面α交于点C,点C不在直线AB上.
解:用符号表示:A∈α,B∈α,a∩α=C,C AB,如图.
题型二:点、线共面问题
例2 如图,已知a α,b α,a∩b=A,P∈b,PQ∥a,求证:PQ α.
证明 因为PQ∥a,
所以PQ与a确定一个平面β,所以直线a β,点P∈β.
因为P∈b,b α,
所以P∈α.
又因为a α,P a,所以α与β重合,所以PQ α.
例3 证明:两两相交且不过同一点的三条直线在同一平面内.
解:已知:如图所示,l1∩l2=A,l2∩l3=B,l1∩l3=C.
求证:直线l1,l2,l3在同一平面内.
证明 方法一
因为l1∩l2=A,所以l1和l2确定一个平面α.
因为l2∩l3=B,所以B∈l2.
又因为l2 α,所以B∈α.
同理可证C∈α.
又因为B∈l3,C∈l3,所以l3 α.
所以直线l1,l2,l3在同一平面内.
方法二
因为l1∩l2=A,所以l1、l2确定一个平面α.
因为l2∩l3=B,所以l2、l3确定一个平面β.
因为A∈l2,l2 α,所以A∈α.
因为A∈l2,l2 β,所以A∈β.
同理可证B∈α,B∈β,C∈α,C∈β.
所以不共线的三个点A、B、C既在平面α内,
又在平面β内.
所以平面α和β重合,
即直线l1,l2,l3在同一平面内.
题型三:证明点共线、线共点问题
例4 如图,E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA
上的点,且直线EH与直线FG交于点O.
求证:B,D,O三点共线.
证明 因为E∈AB,H∈AD,
所以E∈平面ABD,H∈平面ABD.所以EH 平面ABD.
因为EH∩FG=O,所以O∈平面ABD.
同理O∈平面BCD,即O为面ABD与面BCD的公共点,
所以O∈BD,即B,D,O三点共线.
例5 如图,已知平面α,β,且α∩β=l,设梯形ABCD中,AD∥BC,
且AB α,CD β.求证:AB,CD,l共点.
证明 ∵在梯形ABCD中,AD∥BC,
∴AB与CD必交于一点,
设AB交CD于M.
则M∈AB,M∈CD,
又∵AB α,CD β,
∴M∈α,M∈β,
又∵α∩β=l,
∴M∈l,
∴AB,CD,l共点.
1.如果点A在直线a上,而直线a在平面α内,点B在平面α内,则可以表示为
A.A a,a α,B∈α B.A∈a,a α,B∈α
C.A a,a∈α,B α D.A∈a,a∈α,B∈α
解:点A在直线a上,而直线a在平面α内,点B在平面α内,表示为A∈a,a α,B∈α.
故选B.
2.能确定一个平面的条件是
A.空间三个点 B.一个点和一条直线
C.无数个点 D.两条相交直线
解:A项,三个点可能共线,
B项,点可能在直线上,
C项,无数个点也可能在同一条直线上.
故选D.
3.如图,已知D,E是△ABC的边AC,BC上的点,平面α经过D,E两点,若直线AB与平面α的交点是P,则点P与直线DE的位置关系是____________.
解:因为P∈AB,AB 平面ABC,所以P∈平面ABC.
又P∈α,平面ABC∩平面α=DE,所以P∈直线DE.
平面
确定平面的条件
基本事实1
线在面内
基本事实2
点共线、线共点
基本事实3
确定平面的条件
三个推论
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
