6.6.1 柱、锥、台的侧面展开与面积 课件(共15张PPT)2024-2025学年高一数学北师版(2019)必修第二册
文档属性
| 名称 | 6.6.1 柱、锥、台的侧面展开与面积 课件(共15张PPT)2024-2025学年高一数学北师版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 00:00:00 | ||
图片预览

文档简介
(共15张PPT)
第6章 立体几何初步
6.6.1 柱、锥、台的侧面展开与面积
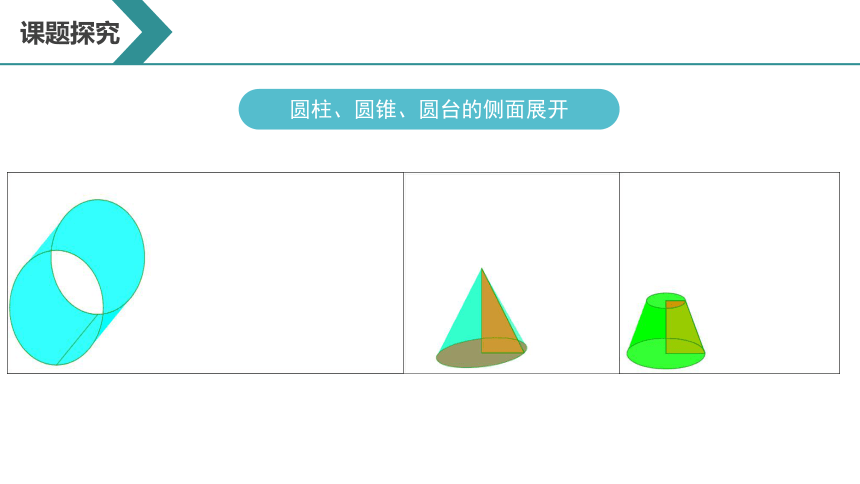
圆柱、圆锥、圆台的侧面展开
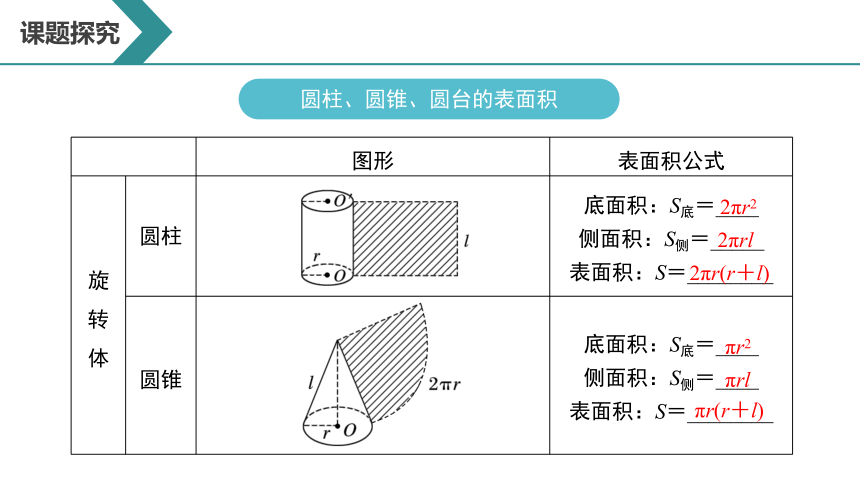
圆柱、圆锥、圆台的表面积
图形 表面积公式
旋 转 体 圆柱 底面积:S底=____
侧面积:S侧=_____
表面积:S=________
圆锥 底面积:S底=____
侧面积:S侧=____
表面积:S=________
2πr2
2πrl
2πr(r+l)
πr2
πrl
πr(r+l)
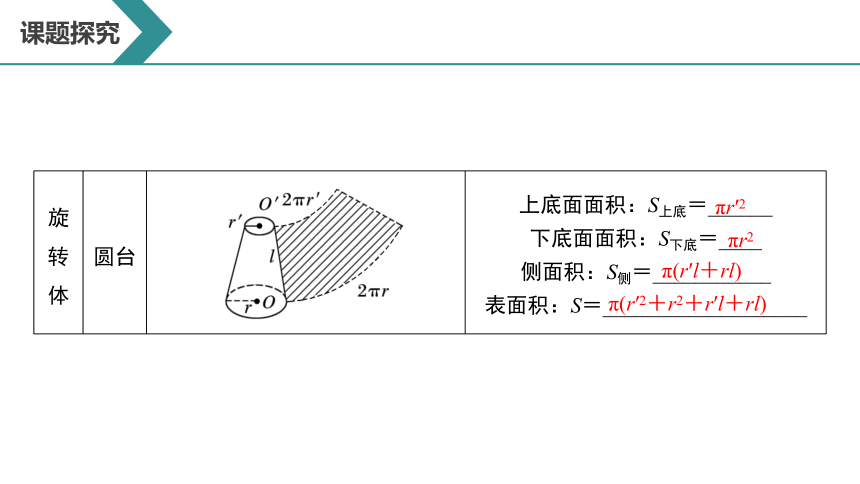
旋 转 体 圆台 上底面面积:S上底=______
下底面面积:S下底=____
侧面积:S侧=___________
表面积:S=___________________
πr′2
πr2
π(r′l+rl)
π(r′2+r2+r′l+rl)
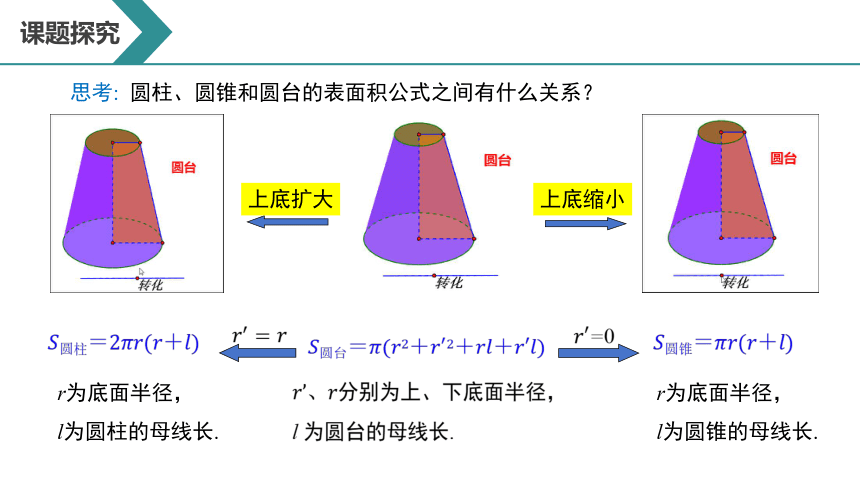
上底缩小
思考: 圆柱、圆锥和圆台的表面积公式之间有什么关系?
r为底面半径,
l为圆锥的母线长.
分别为上、下底面半径,l 为圆台的母线长.
r为底面半径,
l为圆柱的母线长.
上底扩大
=0
题型一:圆柱、圆锥、圆台的表面积
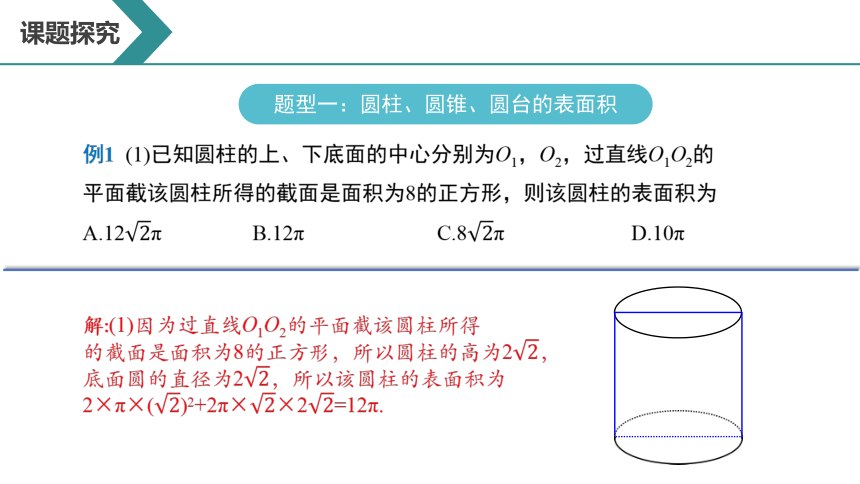
例1 (1)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A.12π B.12π C.8π D.10π
解:(1)因为过直线O1O2的平面截该圆柱所得
的截面是面积为8的正方形,所以圆柱的高为2,
底面圆的直径为2,所以该圆柱的表面积为
2×π×()2+2π××2=12π.
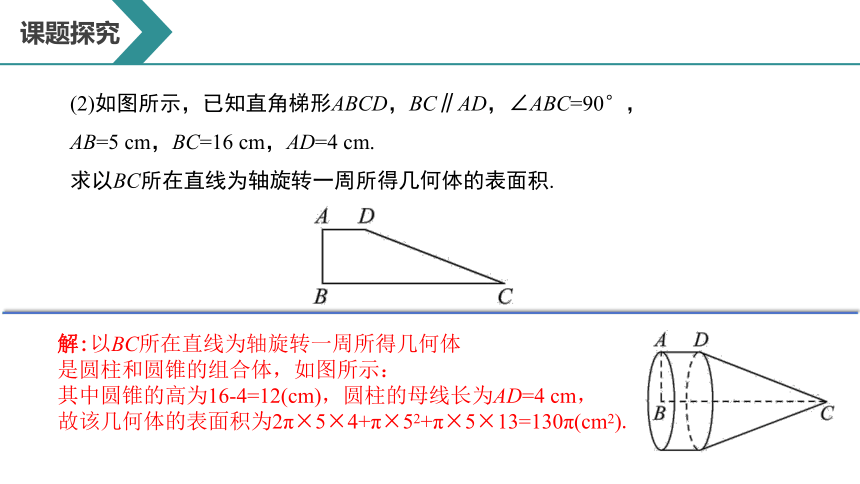
(2)如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,
AB=5 cm,BC=16 cm,AD=4 cm.
求以BC所在直线为轴旋转一周所得几何体的表面积.
解:以BC所在直线为轴旋转一周所得几何体
是圆柱和圆锥的组合体,如图所示:
其中圆锥的高为16-4=12(cm),圆柱的母线长为AD=4 cm,
故该几何体的表面积为2π×5×4+π×52+π×5×13=130π(cm2).
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积
就是围成它们的各个面的面积的和.
棱柱、棱锥、棱台的表面积与其展开图的面积有什么关系?
多面体的表面积就是其展开图的面积,
所以常把多面体展开成平面图形,
利用平面图形求多面体的表面积.
直棱柱、正棱锥、正棱台的侧面展开
题型二:棱柱、棱锥、棱台的表面积
例2 (1)侧面都是等腰直角三角形的正三棱锥,底面边长为a时,
该三棱锥的表面积是
A.a2 B. a2 C. a2 D. a2
解:设正三棱锥的侧棱长为b,
则由条件知,b2+b2=a2,即b2=a2,
所以S=a2+3××a2=a2.故选A.
A
D
B
C
(2)现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,
求该直四棱柱的表面积.
解:设底面对角线AC=a,BD=b,交点为O,
对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
又因为四边形ABCD为菱形,
所以S菱形=AC·BD=
×10×2=20,
所以S表=2S菱形+S侧
=2×20+160=40+160.
∴AB2=2+===64,
1.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比是
解:设底面圆半径为r,母线长为h,∴h=2πr,
则====.
2.一个正四棱台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13 cm,则其表面积为________.
解:由已知可得正四棱台侧面梯形的高为h==12(cm),
所以S侧=4××(8+18)×12=624(cm2),S=8×8=64(cm2),
S下底=18×18=324(cm2),于是表面积为S=624+64+324=1 012(cm2).
3.已知棱长均为5,底面为正方形的四棱锥S-ABCD如图所示,求它的侧面积、表面积.
解: ∵四棱锥S-ABCD的各棱长均为5,
∴各侧面都是全等的正三角形.
设E为AB的中点,连接SE,则SE⊥AB,∴S侧=4S△SAB=4× AB×SE=2×5× =25,S表=S侧+S底=25+25=25(+1).
第6章 立体几何初步
6.6.1 柱、锥、台的侧面展开与面积
圆柱、圆锥、圆台的侧面展开
圆柱、圆锥、圆台的表面积
图形 表面积公式
旋 转 体 圆柱 底面积:S底=____
侧面积:S侧=_____
表面积:S=________
圆锥 底面积:S底=____
侧面积:S侧=____
表面积:S=________
2πr2
2πrl
2πr(r+l)
πr2
πrl
πr(r+l)
旋 转 体 圆台 上底面面积:S上底=______
下底面面积:S下底=____
侧面积:S侧=___________
表面积:S=___________________
πr′2
πr2
π(r′l+rl)
π(r′2+r2+r′l+rl)
上底缩小
思考: 圆柱、圆锥和圆台的表面积公式之间有什么关系?
r为底面半径,
l为圆锥的母线长.
分别为上、下底面半径,l 为圆台的母线长.
r为底面半径,
l为圆柱的母线长.
上底扩大
=0
题型一:圆柱、圆锥、圆台的表面积
例1 (1)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为A.12π B.12π C.8π D.10π
解:(1)因为过直线O1O2的平面截该圆柱所得
的截面是面积为8的正方形,所以圆柱的高为2,
底面圆的直径为2,所以该圆柱的表面积为
2×π×()2+2π××2=12π.
(2)如图所示,已知直角梯形ABCD,BC∥AD,∠ABC=90°,
AB=5 cm,BC=16 cm,AD=4 cm.
求以BC所在直线为轴旋转一周所得几何体的表面积.
解:以BC所在直线为轴旋转一周所得几何体
是圆柱和圆锥的组合体,如图所示:
其中圆锥的高为16-4=12(cm),圆柱的母线长为AD=4 cm,
故该几何体的表面积为2π×5×4+π×52+π×5×13=130π(cm2).
棱柱、棱锥、棱台的表面积
棱柱、棱锥、棱台的表面积
就是围成它们的各个面的面积的和.
棱柱、棱锥、棱台的表面积与其展开图的面积有什么关系?
多面体的表面积就是其展开图的面积,
所以常把多面体展开成平面图形,
利用平面图形求多面体的表面积.
直棱柱、正棱锥、正棱台的侧面展开
题型二:棱柱、棱锥、棱台的表面积
例2 (1)侧面都是等腰直角三角形的正三棱锥,底面边长为a时,
该三棱锥的表面积是
A.a2 B. a2 C. a2 D. a2
解:设正三棱锥的侧棱长为b,
则由条件知,b2+b2=a2,即b2=a2,
所以S=a2+3××a2=a2.故选A.
A
D
B
C
(2)现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,
求该直四棱柱的表面积.
解:设底面对角线AC=a,BD=b,交点为O,
对角线A1C=15,B1D=9,
∴a2+52=152,b2+52=92,
∴a2=200,b2=56.
∵该直四棱柱的底面是菱形,
∴AB=8.
∴直四棱柱的侧面积S=4×8×5=160.
又因为四边形ABCD为菱形,
所以S菱形=AC·BD=
×10×2=20,
所以S表=2S菱形+S侧
=2×20+160=40+160.
∴AB2=2+===64,
1.一个圆柱的侧面展开图是一个正方形,则这个圆柱的表面积与侧面积的比是
解:设底面圆半径为r,母线长为h,∴h=2πr,
则====.
2.一个正四棱台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13 cm,则其表面积为________.
解:由已知可得正四棱台侧面梯形的高为h==12(cm),
所以S侧=4××(8+18)×12=624(cm2),S=8×8=64(cm2),
S下底=18×18=324(cm2),于是表面积为S=624+64+324=1 012(cm2).
3.已知棱长均为5,底面为正方形的四棱锥S-ABCD如图所示,求它的侧面积、表面积.
解: ∵四棱锥S-ABCD的各棱长均为5,
∴各侧面都是全等的正三角形.
设E为AB的中点,连接SE,则SE⊥AB,∴S侧=4S△SAB=4× AB×SE=2×5× =25,S表=S侧+S底=25+25=25(+1).
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
