6.6.3 球的表面积与体积 课件(共15张PPT) 2024-2025学年高一数学北师版(2019)必修第二册
文档属性
| 名称 | 6.6.3 球的表面积与体积 课件(共15张PPT) 2024-2025学年高一数学北师版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 879.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 11:00:38 | ||
图片预览




文档简介
(共15张PPT)
第6章 立体几何初步
6.3 球的表面积与体积
球的表面积和体积
设球的半径为R,则球的表面积S球=4πR2,
球的体积V=πR3.
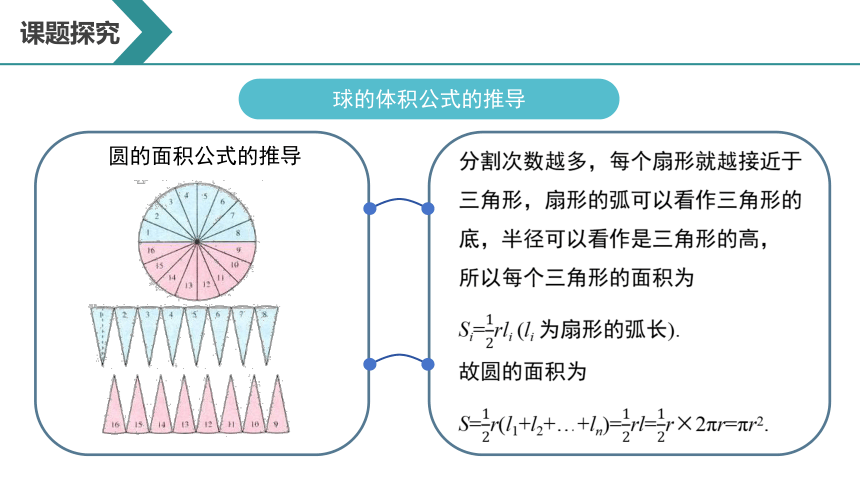
球的体积公式的推导
圆的面积公式的推导
分割次数越多,每个扇形就越接近于
三角形,扇形的弧可以看作三角形的
底,半径可以看作是三角形的高,
所以每个三角形的面积为
Si=rli(li为扇形的弧长).
故圆的面积为
S=r(l1+l2+…+ln)=rl=r×2πr=πr2.
O
D
C
B
A
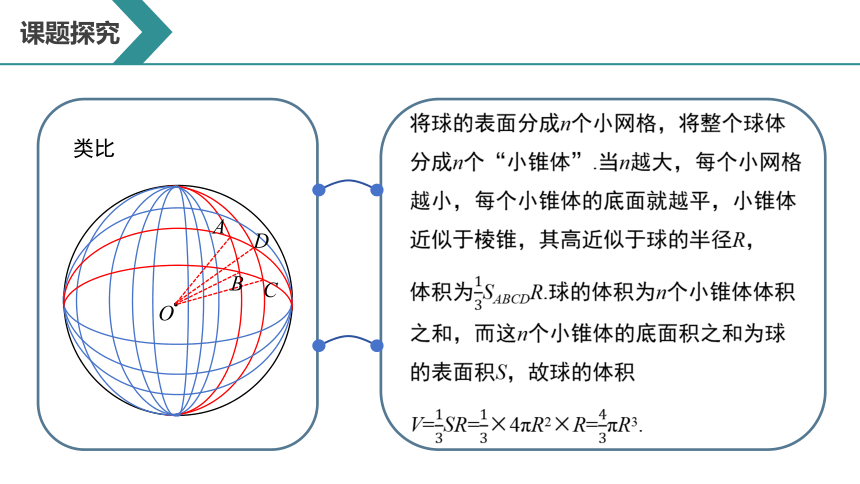
将球的表面分成n个小网格,将整个球体分成n个“小锥体”.当n越大,每个小网格越小,每个小锥体的底面就越平,小锥体近似于棱锥,其高近似于球的半径R,
体积为SABCDR.球的体积为n个小锥体体积之和,而这n个小锥体的底面积之和为球的表面积S,故球的体积V=SR=×4πR2×R=πR3.
类比
例1 (1)已知球的表面积为64π,求它的体积;
解: 设球的半径为R,则4πR2=64π,解得R=4,
所以球的表面积S=4πR2=4π×52=100π.
题型一:球的表面积和体积
解: 设球的半径为R,则πR3=π,解得R=5,
所以球的体积V=πR3=π·43=π.
例2 (1) 过球一条半径的中点,作一垂直于这个半径的截面,截面面积为48π cm2,则球的表面积为____cm2.
解: 易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,
AB是截面圆的直径,作OC垂直AB于点C,连接OA.
由截面面积为48π cm2,可得AC=4cm.
设OA=R,则OC=,所以R2-()2=(4)2,解得R=8.
故球的表面积S=4πR2=256π(cm2).
题型二:球的截面问题
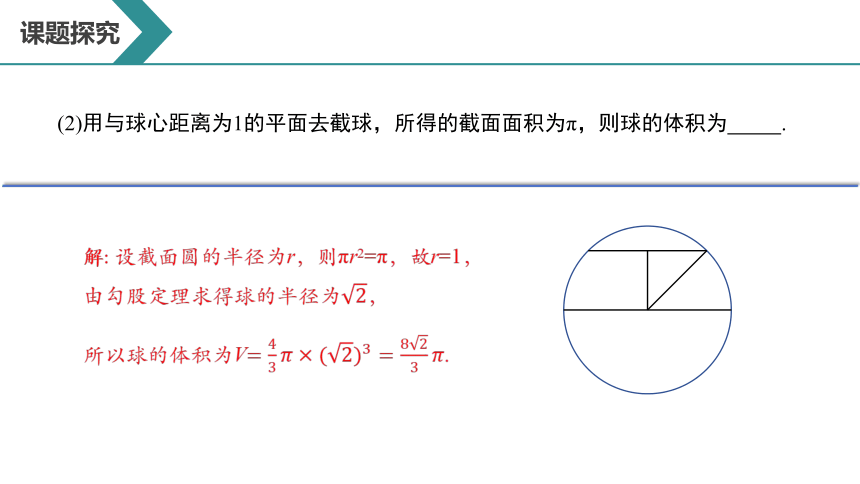
(2)用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为 .
解: 设截面圆的半径为r,则πr2=π,故r=1,
由勾股定理求得球的半径为,
所以球的体积为V= .
题型二:与球有关的切、接问题
例3 (1)将棱长为2的正方体木块削成一个体积最大的球,
则该球的体积为 .
解: 球的直径是正方体的棱长,
所以2R=2,R=1.
所以V=πR3=π.
(2)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,
则球O的表面积为________.
解: 球的直径是长方体的体对角线,
所以2R=,
∴球O的表面积为S=4πR2=14π.
(3)有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,
第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
解: 设正方体的棱长为a,三个球的半径分别为r1,r2,r3,
球的表面积分别为S1,S2,S3.
分别过球心及切点作截面.
如图①所示,有2r1=a,∴r1=,∴S1=πa2.
如图②所示,有2r2=a,∴r2=a,∴S2=2πa2.
如图③所示,有2r3=a,∴r3=a,∴S3=3πa2.
综上可得,S1∶S2∶S3=1∶2∶3.
解: 设球的半径为R,则4πR2=πR3,所以R=3.
解: 设球的半径为R,则由题意可知4πR2=16π,故R=2.
所以球的半径为2,体积V= πR3=π.
3.棱长为a的正四面体的各个顶点都在半径为R的球面上,求其外接球的表面积.
解: 把正四面体放在正方体中,设正方体棱长为x,则a=x,
由题意2R=x=a, 所以R=a,所以S球=4πR2=a2π.
4.如图,圆柱形容器内盛有高度为6 cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为
A.4 cm B.3 cm
C.2 cm D.1 cm
解: 由题意可得,设球的半径为r,
依题意得三个球的体积和水的体积之和等于圆柱体的体积,
解得r=3,故选B.
∴3× πr3=πr2(6r-6),
第6章 立体几何初步
6.3 球的表面积与体积
球的表面积和体积
设球的半径为R,则球的表面积S球=4πR2,
球的体积V=πR3.
球的体积公式的推导
圆的面积公式的推导
分割次数越多,每个扇形就越接近于
三角形,扇形的弧可以看作三角形的
底,半径可以看作是三角形的高,
所以每个三角形的面积为
Si=rli(li为扇形的弧长).
故圆的面积为
S=r(l1+l2+…+ln)=rl=r×2πr=πr2.
O
D
C
B
A
将球的表面分成n个小网格,将整个球体分成n个“小锥体”.当n越大,每个小网格越小,每个小锥体的底面就越平,小锥体近似于棱锥,其高近似于球的半径R,
体积为SABCDR.球的体积为n个小锥体体积之和,而这n个小锥体的底面积之和为球的表面积S,故球的体积V=SR=×4πR2×R=πR3.
类比
例1 (1)已知球的表面积为64π,求它的体积;
解: 设球的半径为R,则4πR2=64π,解得R=4,
所以球的表面积S=4πR2=4π×52=100π.
题型一:球的表面积和体积
解: 设球的半径为R,则πR3=π,解得R=5,
所以球的体积V=πR3=π·43=π.
例2 (1) 过球一条半径的中点,作一垂直于这个半径的截面,截面面积为48π cm2,则球的表面积为____cm2.
解: 易知截面为一圆面,如图所示,圆O是球的过已知半径的大圆,
AB是截面圆的直径,作OC垂直AB于点C,连接OA.
由截面面积为48π cm2,可得AC=4cm.
设OA=R,则OC=,所以R2-()2=(4)2,解得R=8.
故球的表面积S=4πR2=256π(cm2).
题型二:球的截面问题
(2)用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为 .
解: 设截面圆的半径为r,则πr2=π,故r=1,
由勾股定理求得球的半径为,
所以球的体积为V= .
题型二:与球有关的切、接问题
例3 (1)将棱长为2的正方体木块削成一个体积最大的球,
则该球的体积为 .
解: 球的直径是正方体的棱长,
所以2R=2,R=1.
所以V=πR3=π.
(2)长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,
则球O的表面积为________.
解: 球的直径是长方体的体对角线,
所以2R=,
∴球O的表面积为S=4πR2=14π.
(3)有三个球,第一个球内切于正方体,第二个球与这个正方体各条棱相切,
第三个球过这个正方体的各个顶点,求这三个球的表面积之比.
解: 设正方体的棱长为a,三个球的半径分别为r1,r2,r3,
球的表面积分别为S1,S2,S3.
分别过球心及切点作截面.
如图①所示,有2r1=a,∴r1=,∴S1=πa2.
如图②所示,有2r2=a,∴r2=a,∴S2=2πa2.
如图③所示,有2r3=a,∴r3=a,∴S3=3πa2.
综上可得,S1∶S2∶S3=1∶2∶3.
解: 设球的半径为R,则4πR2=πR3,所以R=3.
解: 设球的半径为R,则由题意可知4πR2=16π,故R=2.
所以球的半径为2,体积V= πR3=π.
3.棱长为a的正四面体的各个顶点都在半径为R的球面上,求其外接球的表面积.
解: 把正四面体放在正方体中,设正方体棱长为x,则a=x,
由题意2R=x=a, 所以R=a,所以S球=4πR2=a2π.
4.如图,圆柱形容器内盛有高度为6 cm的水,若放入3个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球,则球的半径为
A.4 cm B.3 cm
C.2 cm D.1 cm
解: 由题意可得,设球的半径为r,
依题意得三个球的体积和水的体积之和等于圆柱体的体积,
解得r=3,故选B.
∴3× πr3=πr2(6r-6),
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
