6.2二次函数的图象与性质

课件27张PPT。苏科版九年级下册 6.2节热烈欢迎各位专家
莅临指导
导学人:徐新亮
1.二次函数y=ax2、y=ax2+k图象是什么？ 忆一忆抛物线2. 二次函数 y=ax2+k的图象是由二次函数 y=ax2的图象怎样运动得到？若k ＞0时,抛物线y=ax2向上平移k个单位得抛物线 :y=ax2+k若k ＜0时,抛物线y=ax2向下平移 个单位
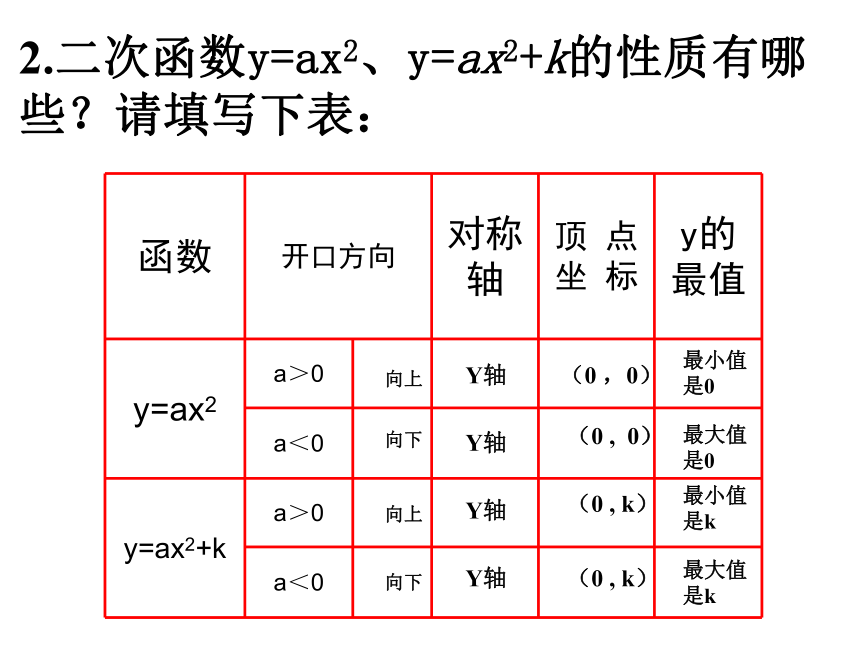
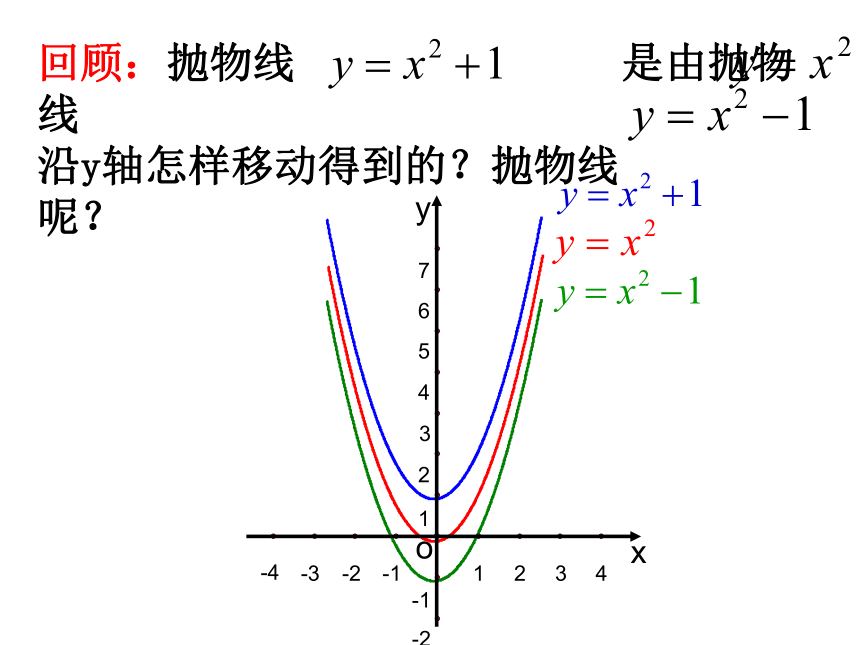
得抛物线 :y=ax2+k2.二次函数y=ax2、y=ax2+k的性质有哪些？请填写下表：向上Y轴（0 ，0）最小值是0向下Y轴（0 , 0）最大值是0向上Y轴（0 , k）最小值是k向下Y轴（0 , k）最大值是k回顾：抛物线 是由抛物线
沿y轴怎样移动得到的？抛物线
呢？
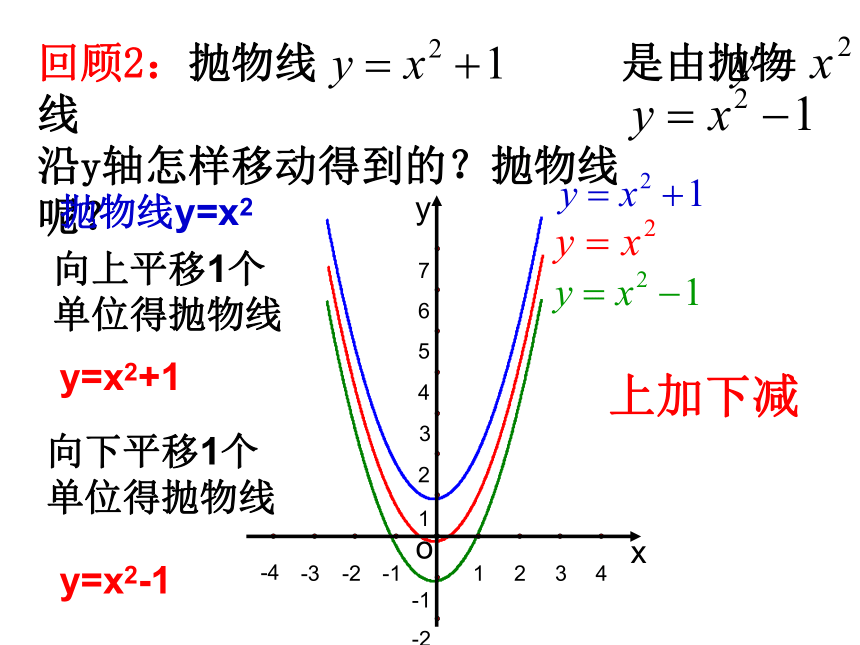
回顾2：抛物线 是由抛物线
沿y轴怎样移动得到的？抛物线
呢？
抛物线y=x2向上平移1个单位得抛物线
y=x2+1向下平移1个单位得抛物线
y=x2-1
上加下减
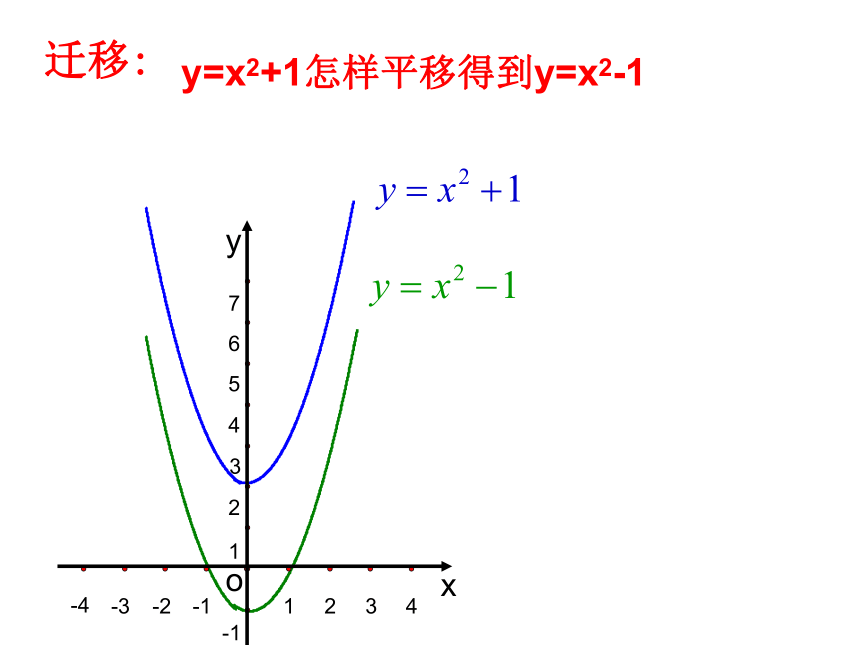
迁移:y=x2+1怎样平移得到y=x2-1情境创设我们知道函数y=ax2的图象上下平移可以得到函数y=ax2+k的图象。那么函数y=ax2 的图象左右平移又会怎样呢？ 二次函数
的图象和性质
y=a(x-h)2 在同一直角坐标系内画出函数

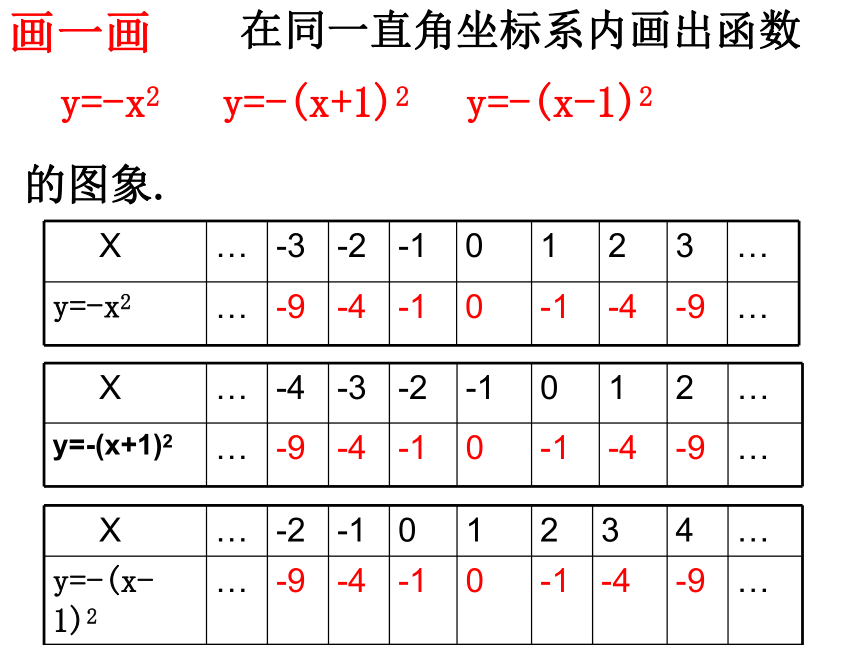
的图象. y=-x2y=-(x+1)2y=-(x-1)2画一画问题1 在同一直角坐标系内画出函数

的图象. y=-x2y=-(x+1)2y=-(x-1)2探究1:抛物线
的开口方向，对称轴，顶点坐标有何异同？x=-1x=1x=0顶点(-1,0)(0,0)(1,0)开口方向:向下y=-x2y=-(x+1)2y=-(x-1)2探究2:抛物线 是由抛物线
沿x轴怎样移动得到的？抛物线 呢？
y=-x2y=-(x+1)2y=-(x-1)2探究2:抛物线 是由抛物线
沿x轴怎样移动得到的？抛物线 呢？
y=-x2y=-(x+1)2y=-(x-1)2抛物线向左平移1个单位得抛物线向右平移1个单位得抛物线左加右减y=-x2y=-(x+1)2y=-(x-1)2抛物线 的性质：(1)a＞0时,开口向上;a＜0时,开口向下；(2)对称轴为直线x=h； (4)若h＞0，则它的图象由y=ax2向右平移 h个单位得到;
若h＜0，则它的图象由y=ax2向左平移|h|个单位得到． 小 结左加右减
(3)顶点坐标(h ,０)练习三解(1)∵a=-3<0∴开口向下对称轴:直线 x= 1顶点:(1，0)（1）y=-3(x-1)2 (2)y=4(x-3)2 (3)y=2(x+3)2解(2)∵a=4>0∴开口向上对称轴:直线 x=3顶点:(3,0)练习三1.说出下列抛物线的开口方向、
对称轴及 顶点坐标：解(3)∵a=2>0∴开口向上对称轴:直线 x=-3顶点:(-3,0)(3)y=2(x+3)2y=2〔x-(-3)〕21.说出下列抛物线的开口方向、对称轴及 顶点坐标：
巩固练习y=-(x-3)2
y=2(x-4)2
(3)y=3(x+4)2y=3(x+2)21.已知抛物线y=3x2y=3(x-3)2例2y=3(x+5)2y=3(x-1)2y=2x2右3巩固练习y=-3(x+3)2拓 展 (1)怎样平移抛物线y=3x2可以得到抛物线y=3(x-2)2-3?
y=3x2y=3x2-3y=3(x-2)2-3
下 3右 2y=3x2y=3(x-2)2-3y=3(x-2)2下 3右 2（2）把抛物线y=a（x－4）2向左平移6个单位后得到抛物线y=－ 3（x-h）2的图象，若抛物线y= a（x－4）2的顶点A，且与y轴交于点B，抛物线y= － 3（x－h）2的顶点是M，求ΔMAB的面积.sΔMAB=144a=-3 h=-2谈谈收获：通过本节课的学习，你有哪些收获？课堂作业
P10 　4，5题在数学的天地里，重要的不是我们
知道什么，而是我们怎么知道什么!
——毕达哥拉斯 谢谢指导！