浙江省杭州地区(含周边)重点中学2024-2025学年高一下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 浙江省杭州地区(含周边)重点中学2024-2025学年高一下学期期中考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 923.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-26 23:33:48 | ||
图片预览


文档简介
绝密★考试结束前
2 0 2 4 学 年 第 二 学 期 期 中 杭 州 地 区 ( 含 周 边 ) 重 点 中 学
高一年级数学学科试题
考生须知:
1、本卷满分150分,考试时间120分钟:
2. 答题前、在答题卷密封区内填写班级、考试号和姓名:
3、所有答案必须写在答题卷上,写在试卷上无效;
4. 考试结束后、只需上交答题卷.
第 I 卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合 题目要求的
1、设A={0,1,2,3},B={x|(x-1)(x-2)>0}, 则A∩B=
A.{0,1} B.{0,3} C.{1,2} D.{2,3}
2. 设(l+ai)(a-i)=2,a∈R, 则a=
A.-1 B.0 C.1 D.2
3. 已知向量a=(3,4),b=(5,0),那么向量a在向量b 上的投影向量为
A.3 B.5 C.(3,0) D.
4. 在△ABC中,, 则 1 ’是“△ABC 是钝角三角形”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知 , 则tana ·tanβ=
A.3 B.1 C. D.
6. 若函数,(a>0 且a≠1)满足:对于任意x,x eR 且x ≠x , 都有 (x -x )[f(x )-f(x )]<0 成立,则实数a的取值范围是
B. D.
7. 在△ABC中,角A,B,C的对边分别是a,b,c, 下列说法正确的是
A. 若 a=b=c=2, 则 AB·BC=2
B. 若 ,a= √2,c=2, 则b= √3+1
C. 若acos A=bcos B,则△ABC是等腰三角形
D. 若a=2,b=2√2, 满足△ABC有解,则
高一数学试题卷 第 1 页 共 4 页
8. 已知函数 的最小正周期为元,当 时,函数f(x) 取 得最大值、则
A.f(1)>(3)>f(5) B.f(3)>f(1)>f(5)
C.f(5) f(3) f(1) D.f(3)>f(5)>f(1)
二、选择题:本题共3小题、每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全 部选对的得6分、部分选对的得部分分,有选错的得0分.
0. 若复数z=-1+2i 、 则下列说法正确的是
A.z 的虚部是2i B.z=-1-2i
C.z=√5 D. 在复平面内对应的点在第二象限
10. 如图、已知圆台形水杯盛有牛奶(不计厚度),杯口的直径为4,杯底的直径为2,杯高为4,当 杯底水平放置时,牛奶面的高度为水杯高度的一半,若加入37颗大小相同的椰果(球形),椰 果沉入杯底,牛奶恰好充满水杯,则
A、 该水杯侧面积为12π
B、 该水杯里牛奶的体积为
C. 放入的椰果半径为
D. 该水杯外接球的表面积为
11. 在△ABC 中 ,D 是 AC 中点,CB=2BE, 且 DE 交 AB 于 F, 则 A.F 为 DE 的中点
B.
C. 若AB⊥BC, 且 |AB|=2, 则AB ·DE=2
D. 若AB⊥D E, 则∠ACB 的最大值为
第 Ⅱ 卷
三 、填空题:本题共3小题,每小题5分,共15分.
12. 已知圆锥的底面半径为1,侧面展开图是圆心角为 的扇形,则该圆锥的表面积为 ▲
13. 如图,为了测量两山顶M,N 间的距离,飞机沿水平方向在A,B 两点进行测量, A,B,M,N 在同 一 铅垂平面内,飞机在A点 到M,N 点的俯角分别为75°,30°,飞行3千米后,在B 点 到M,N 点的 俯角分别为45°,60°,则测得两山顶M,N 间距离为_ 千米.
高一数学试题卷 第 2 页 共 4 页
14、设O 为AABC 的外心,若 则cos ∠BAC等于 ▲ _
四、解答题:本题共5小题、共77分.解答应写出文字说明、证明过程或演算步骤.
15 . (本题满分13分)若e .e 是夹角为60°的两个单位向量,已知向量a=2e +e .b=Ae+2e
(1)若向量a,b 共线,求实数λ的值:
(2)若λ=-3,求向量a,b的夹角
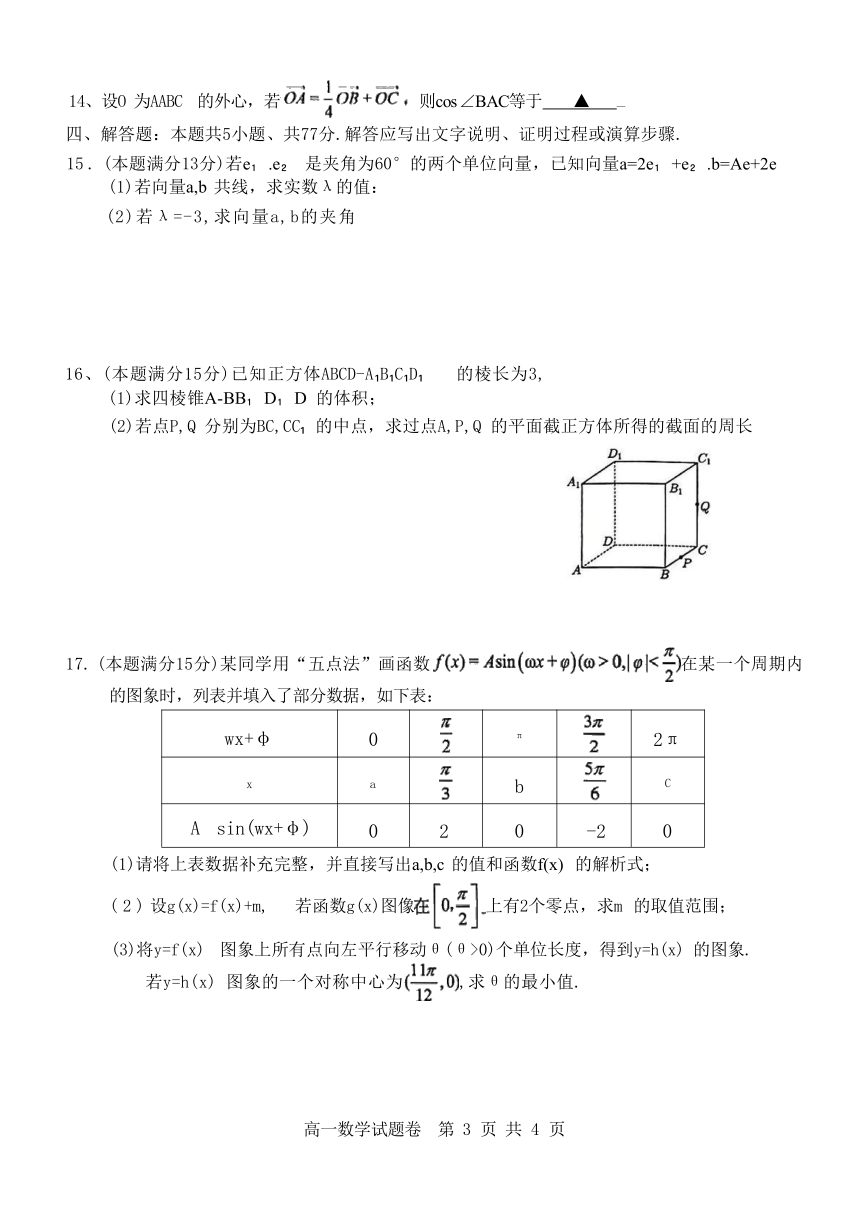
16、(本题满分15分)已知正方体ABCD-A B C D 的棱长为3, (1)求四棱锥A-BB D D 的体积;
(2)若点P,Q 分别为BC,CC 的中点,求过点A,P,Q 的平面截正方体所得的截面的周长
17. (本题满分15分)某同学用“五点法”画函数 在某一个周期内 的图象时,列表并填入了部分数据,如下表:
wx+φ 0 π 2π
x a b C
A sin(wx+φ) 0 2 0 -2 0
(1)请将上表数据补充完整,并直接写出a,b,c 的值和函数f(x) 的解析式;
( 2 ) 设g(x)=f(x)+m, 若函数g(x)图像上有2个零点,求m 的取值范围;
(3)将y=f(x) 图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=h(x) 的图象. 若y=h(x) 图象的一个对称中心为,求θ的最小值.
高一数学试题卷 第 3 页 共 4 页
18 . (本题满分17分)已知函数f(x) 的定义域为R, 现有下面两种对f(x) 变换的操作:
Φ变换:f(x)→f(x)-f(x-1);
W变换:f(x)→f(x+1)-f(x)|, 其 中t>0.
( 1 ) 若f(x)=3*,1=1, 对f(x) 进行Φ变换后得到函数g(x), 解方程g(x)=2;
(2)若 , 对f(x)进行W 变换后得到函数h(x), 解不等式h(x)<1;
(3)定义:先对f(x) 进行Φ变换得到函数g(x)=f(x)-f(x-1); 再对g(x) 进行の变换得到函 数h(x)=g(x+1)-g(x)|. 设F(x)=h(x-a)+b,(a,b∈R). 证明:无论f(x) 是奇函数还是偶 函数,函数F(x) 的图像总关于直线x=a 对称.
19. (本题满分17分)如图,在△ABC中 ,D,E 为BC 边上的三等分点, BC=3√3,
( 1 ) 若AE=2√3, 求△ABC的面积;
( 2 ) 求AC 长的最大值;
(3)若∠BAE=∠CAD, 求 cos ∠DAE的值.
高一数学试题卷 第 4 页 共 4 页
2024学年第二学期期中杭州地区(含周边)重点中学 高一年级数学学科参考答案
一 、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合 题目要求的.
题号 1 2 3 4 5 6 7 8
答案 B C C A D C D A
二 、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全 部选对的得6分,部分选对的得部分分,有选错的得0分.
题号 9 10 11
答案 BC BCD ACD
三、填空题:本题共3小题,每小题5分,共15分。
12.4π 13. √ 15 14.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤
15. (1)由向量a,b 共线可知,存在实数t, 使得a=tb, 即 2e+e=z(ae+2e ) 因 此 ( 2 -ta)e=(2t-1)e ,
由于e,e 不共线,必有2-ta=2t-1=0, 解得λ=4 … … … … … … … 5分
(2)因为 ;
同= √ (2+e ) =√40 +4e·eE+e =57:
同= √ {-3e+2) =Jse -12e·E+4 =√7;
得,向量a,b 的夹角为120°. ……………………13分
16. (1)由正方体特征知,
(2)如图,延长PQ 交 B C 于点M, 延长QP 交 B B 于点N, 连接 A M 交 C D 于点F, 连接A N 交 AB 于点E, 连接FQ,EP.则过 点A P,Q 的平面截正方体所得的截面为五边形A EPQF.
因为P 为BC 的中点,Q 为CC 的中点,
所以
所以
所以A E=A F= √ 13,
高 一 数学参考答案第1页 共 3 页
即截面周长为
17. (1)根据表中已知数据,解得
……………5分
(2)若函数g(x)图像在上有2个零点,即
个交点.
由0≤x≤π得,
结合f(x)=2sinx 图像知:-2因为y=2sinx 的对称中心为(kπ,0),k∈Z.
……………………15分
,A=2,w=2,
与y=-m 在 上有2
……………………10分
高一数学参考答案 第 2 页 共 3 页
令 ,解得 ,k∈Z.
由于函数y=h(x) 的图象关于点成中心对称,令
解 k∈Z. 由θ>0可知,当k=2 时,θ取得最小值.…… ………15分
18. (1)由φ变换得:g(x)=f(x)-f(x-1)=3*-3*- =2, 解得x=1 4 分
(2)由w 变换得:
解不等式 1得:
(
即
) (
故:解集
,
)
∈Z
…………
10分
(3)由w 变换得:g(x)=f(x)-f(x-t); 由w 变换得:h(x)=|g(x+t)-g(x)| 即h(x)=|f(x+t)-f(x)-[f(x)-f(x-1)]=|f(x+t)+f(x-t)-2f(x)
若f(x)是奇函数,得f(-x)=-f(x),f(-x-t)=-f(x+t),
由h(-x)=|f(-x+t)+f(-x-t)-2f(-x) |=|f(x-t)+f(x+t)-2f(x) |=h(x), 所以h(x)是偶函数.
若f(x) 是偶函数,得f(-x)=f(x),f(-x-t)=f(x+t),
由h(-x)=|f(-x+t)+f(-x-t)-2f(-x) |=|f(x-t)+f(x+t)-2f(x) |=h(x),
所以h(x) 是偶函数.
所以无论f(x) 是奇函数还是偶函数,h(x)都是偶函数,
则F(x) 图像总关于直线x=a 对称. (请酌情给分) ……………………17分
19 . (1)在△ABE中 , 由AE=BE 且 得△ABE 为正三角形,
……………………………4分
(2)在△ABE 中,由正弦定理得, 即 , 所 以AE=4sinB 在△ACE 中,
=28sin B-4√3sinBcosB+3=17-4√ 13sin(2B+0) (其中
因为
, 所 以
又因为 , 所 以sin(2B+0) 可取到最小值-1.
所以AC ≤17+4√ 13=(2+√ 13) , , 即AC 最大值为2+ √ 13 …………………10分
(3)设∠ DAE=θ, 由对称性知
所以 在△ADE中 , 即
则
,
所 以
在△ABE 中, , 即, 所 以 所以 ,化简得:
因为 , 所 以, 所 以
, 即
…………………
17分
高一数学参考答案 第 3 页 共 3 页
2 0 2 4 学 年 第 二 学 期 期 中 杭 州 地 区 ( 含 周 边 ) 重 点 中 学
高一年级数学学科试题
考生须知:
1、本卷满分150分,考试时间120分钟:
2. 答题前、在答题卷密封区内填写班级、考试号和姓名:
3、所有答案必须写在答题卷上,写在试卷上无效;
4. 考试结束后、只需上交答题卷.
第 I 卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合 题目要求的
1、设A={0,1,2,3},B={x|(x-1)(x-2)>0}, 则A∩B=
A.{0,1} B.{0,3} C.{1,2} D.{2,3}
2. 设(l+ai)(a-i)=2,a∈R, 则a=
A.-1 B.0 C.1 D.2
3. 已知向量a=(3,4),b=(5,0),那么向量a在向量b 上的投影向量为
A.3 B.5 C.(3,0) D.
4. 在△ABC中,, 则 1 ’是“△ABC 是钝角三角形”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
5. 已知 , 则tana ·tanβ=
A.3 B.1 C. D.
6. 若函数,(a>0 且a≠1)满足:对于任意x,x eR 且x ≠x , 都有 (x -x )[f(x )-f(x )]<0 成立,则实数a的取值范围是
B. D.
7. 在△ABC中,角A,B,C的对边分别是a,b,c, 下列说法正确的是
A. 若 a=b=c=2, 则 AB·BC=2
B. 若 ,a= √2,c=2, 则b= √3+1
C. 若acos A=bcos B,则△ABC是等腰三角形
D. 若a=2,b=2√2, 满足△ABC有解,则
高一数学试题卷 第 1 页 共 4 页
8. 已知函数 的最小正周期为元,当 时,函数f(x) 取 得最大值、则
A.f(1)>(3)>f(5) B.f(3)>f(1)>f(5)
C.f(5) f(3) f(1) D.f(3)>f(5)>f(1)
二、选择题:本题共3小题、每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全 部选对的得6分、部分选对的得部分分,有选错的得0分.
0. 若复数z=-1+2i 、 则下列说法正确的是
A.z 的虚部是2i B.z=-1-2i
C.z=√5 D. 在复平面内对应的点在第二象限
10. 如图、已知圆台形水杯盛有牛奶(不计厚度),杯口的直径为4,杯底的直径为2,杯高为4,当 杯底水平放置时,牛奶面的高度为水杯高度的一半,若加入37颗大小相同的椰果(球形),椰 果沉入杯底,牛奶恰好充满水杯,则
A、 该水杯侧面积为12π
B、 该水杯里牛奶的体积为
C. 放入的椰果半径为
D. 该水杯外接球的表面积为
11. 在△ABC 中 ,D 是 AC 中点,CB=2BE, 且 DE 交 AB 于 F, 则 A.F 为 DE 的中点
B.
C. 若AB⊥BC, 且 |AB|=2, 则AB ·DE=2
D. 若AB⊥D E, 则∠ACB 的最大值为
第 Ⅱ 卷
三 、填空题:本题共3小题,每小题5分,共15分.
12. 已知圆锥的底面半径为1,侧面展开图是圆心角为 的扇形,则该圆锥的表面积为 ▲
13. 如图,为了测量两山顶M,N 间的距离,飞机沿水平方向在A,B 两点进行测量, A,B,M,N 在同 一 铅垂平面内,飞机在A点 到M,N 点的俯角分别为75°,30°,飞行3千米后,在B 点 到M,N 点的 俯角分别为45°,60°,则测得两山顶M,N 间距离为_ 千米.
高一数学试题卷 第 2 页 共 4 页
14、设O 为AABC 的外心,若 则cos ∠BAC等于 ▲ _
四、解答题:本题共5小题、共77分.解答应写出文字说明、证明过程或演算步骤.
15 . (本题满分13分)若e .e 是夹角为60°的两个单位向量,已知向量a=2e +e .b=Ae+2e
(1)若向量a,b 共线,求实数λ的值:
(2)若λ=-3,求向量a,b的夹角
16、(本题满分15分)已知正方体ABCD-A B C D 的棱长为3, (1)求四棱锥A-BB D D 的体积;
(2)若点P,Q 分别为BC,CC 的中点,求过点A,P,Q 的平面截正方体所得的截面的周长
17. (本题满分15分)某同学用“五点法”画函数 在某一个周期内 的图象时,列表并填入了部分数据,如下表:
wx+φ 0 π 2π
x a b C
A sin(wx+φ) 0 2 0 -2 0
(1)请将上表数据补充完整,并直接写出a,b,c 的值和函数f(x) 的解析式;
( 2 ) 设g(x)=f(x)+m, 若函数g(x)图像上有2个零点,求m 的取值范围;
(3)将y=f(x) 图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=h(x) 的图象. 若y=h(x) 图象的一个对称中心为,求θ的最小值.
高一数学试题卷 第 3 页 共 4 页
18 . (本题满分17分)已知函数f(x) 的定义域为R, 现有下面两种对f(x) 变换的操作:
Φ变换:f(x)→f(x)-f(x-1);
W变换:f(x)→f(x+1)-f(x)|, 其 中t>0.
( 1 ) 若f(x)=3*,1=1, 对f(x) 进行Φ变换后得到函数g(x), 解方程g(x)=2;
(2)若 , 对f(x)进行W 变换后得到函数h(x), 解不等式h(x)<1;
(3)定义:先对f(x) 进行Φ变换得到函数g(x)=f(x)-f(x-1); 再对g(x) 进行の变换得到函 数h(x)=g(x+1)-g(x)|. 设F(x)=h(x-a)+b,(a,b∈R). 证明:无论f(x) 是奇函数还是偶 函数,函数F(x) 的图像总关于直线x=a 对称.
19. (本题满分17分)如图,在△ABC中 ,D,E 为BC 边上的三等分点, BC=3√3,
( 1 ) 若AE=2√3, 求△ABC的面积;
( 2 ) 求AC 长的最大值;
(3)若∠BAE=∠CAD, 求 cos ∠DAE的值.
高一数学试题卷 第 4 页 共 4 页
2024学年第二学期期中杭州地区(含周边)重点中学 高一年级数学学科参考答案
一 、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合 题目要求的.
题号 1 2 3 4 5 6 7 8
答案 B C C A D C D A
二 、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全 部选对的得6分,部分选对的得部分分,有选错的得0分.
题号 9 10 11
答案 BC BCD ACD
三、填空题:本题共3小题,每小题5分,共15分。
12.4π 13. √ 15 14.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤
15. (1)由向量a,b 共线可知,存在实数t, 使得a=tb, 即 2e+e=z(ae+2e ) 因 此 ( 2 -ta)e=(2t-1)e ,
由于e,e 不共线,必有2-ta=2t-1=0, 解得λ=4 … … … … … … … 5分
(2)因为 ;
同= √ (2+e ) =√40 +4e·eE+e =57:
同= √ {-3e+2) =Jse -12e·E+4 =√7;
得,向量a,b 的夹角为120°. ……………………13分
16. (1)由正方体特征知,
(2)如图,延长PQ 交 B C 于点M, 延长QP 交 B B 于点N, 连接 A M 交 C D 于点F, 连接A N 交 AB 于点E, 连接FQ,EP.则过 点A P,Q 的平面截正方体所得的截面为五边形A EPQF.
因为P 为BC 的中点,Q 为CC 的中点,
所以
所以
所以A E=A F= √ 13,
高 一 数学参考答案第1页 共 3 页
即截面周长为
17. (1)根据表中已知数据,解得
……………5分
(2)若函数g(x)图像在上有2个零点,即
个交点.
由0≤x≤π得,
结合f(x)=2sinx 图像知:-2
……………………15分
,A=2,w=2,
与y=-m 在 上有2
……………………10分
高一数学参考答案 第 2 页 共 3 页
令 ,解得 ,k∈Z.
由于函数y=h(x) 的图象关于点成中心对称,令
解 k∈Z. 由θ>0可知,当k=2 时,θ取得最小值.…… ………15分
18. (1)由φ变换得:g(x)=f(x)-f(x-1)=3*-3*- =2, 解得x=1 4 分
(2)由w 变换得:
解不等式 1得:
(
即
) (
故:解集
,
)
∈Z
…………
10分
(3)由w 变换得:g(x)=f(x)-f(x-t); 由w 变换得:h(x)=|g(x+t)-g(x)| 即h(x)=|f(x+t)-f(x)-[f(x)-f(x-1)]=|f(x+t)+f(x-t)-2f(x)
若f(x)是奇函数,得f(-x)=-f(x),f(-x-t)=-f(x+t),
由h(-x)=|f(-x+t)+f(-x-t)-2f(-x) |=|f(x-t)+f(x+t)-2f(x) |=h(x), 所以h(x)是偶函数.
若f(x) 是偶函数,得f(-x)=f(x),f(-x-t)=f(x+t),
由h(-x)=|f(-x+t)+f(-x-t)-2f(-x) |=|f(x-t)+f(x+t)-2f(x) |=h(x),
所以h(x) 是偶函数.
所以无论f(x) 是奇函数还是偶函数,h(x)都是偶函数,
则F(x) 图像总关于直线x=a 对称. (请酌情给分) ……………………17分
19 . (1)在△ABE中 , 由AE=BE 且 得△ABE 为正三角形,
……………………………4分
(2)在△ABE 中,由正弦定理得, 即 , 所 以AE=4sinB 在△ACE 中,
=28sin B-4√3sinBcosB+3=17-4√ 13sin(2B+0) (其中
因为
, 所 以
又因为 , 所 以sin(2B+0) 可取到最小值-1.
所以AC ≤17+4√ 13=(2+√ 13) , , 即AC 最大值为2+ √ 13 …………………10分
(3)设∠ DAE=θ, 由对称性知
所以 在△ADE中 , 即
则
,
所 以
在△ABE 中, , 即, 所 以 所以 ,化简得:
因为 , 所 以, 所 以
, 即
…………………
17分
高一数学参考答案 第 3 页 共 3 页
同课章节目录
