9.4 探索三角形相似的条件 解答专项练习题(含答案)鲁教版八年级数学下册
文档属性
| 名称 | 9.4 探索三角形相似的条件 解答专项练习题(含答案)鲁教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-27 10:23:31 | ||
图片预览



文档简介
鲁教版八年级数学下册《9.4探索三角形相似的条件》
解答专项练习题(附答案)
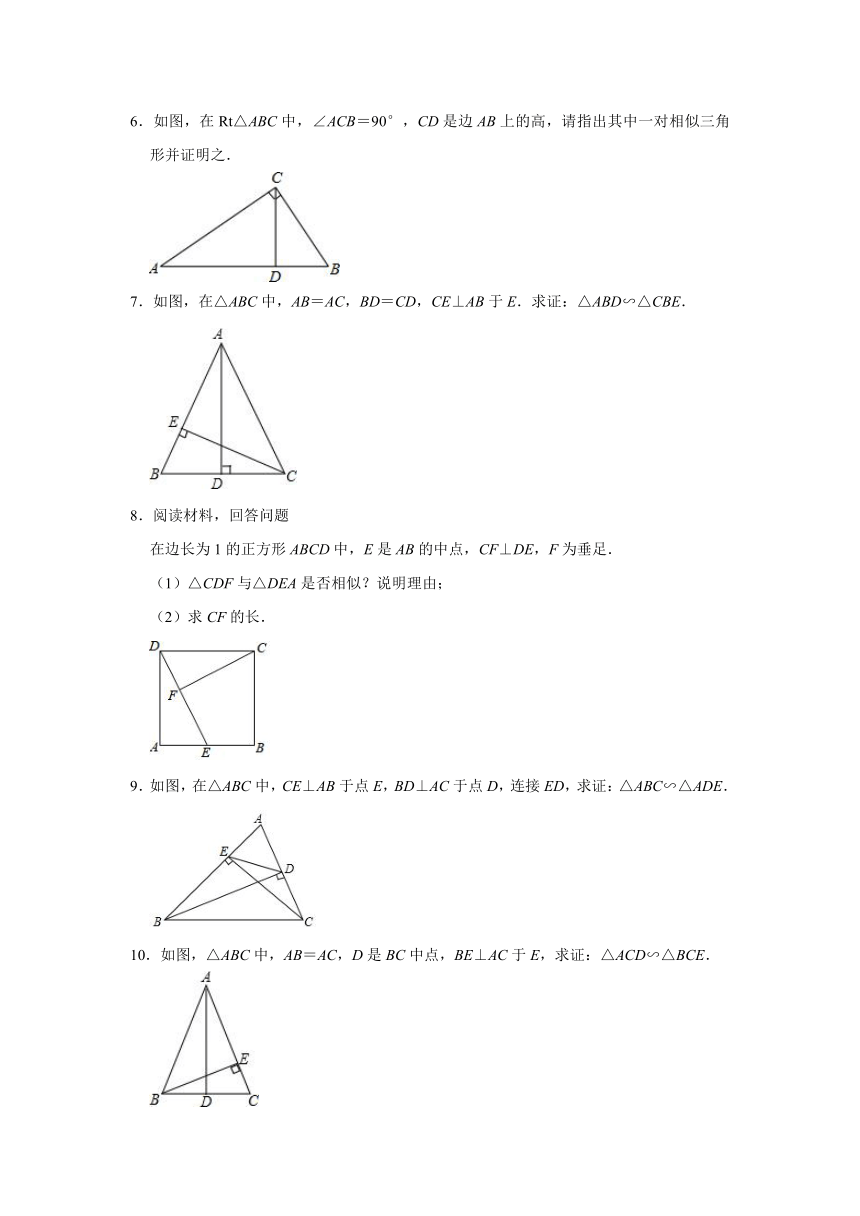
1.已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB.求证:△CDF∽△ECF.
2.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于点F,OE⊥OB交BC边于点E.求证:△ABF∽△COE.
3.如图,在矩形ABCD中,E是AD边上的一点,BE⊥AC,垂足为点F.求证:△AEF∽△CAB.
4.如图,D是△ABC的边AB上的一点,BD=2,AB=,BC=3.求证:△BCD∽△BAC.
5.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
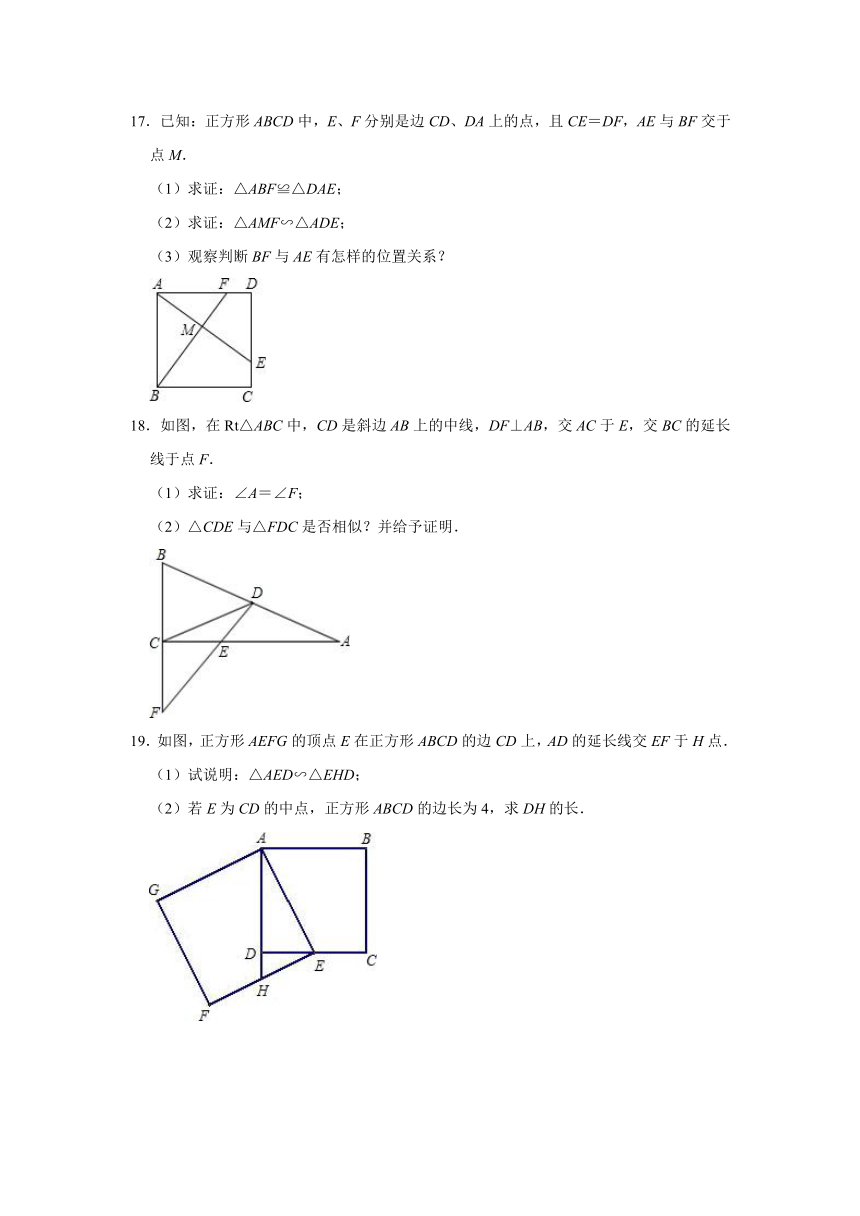
6.如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高,请指出其中一对相似三角形并证明之.
7.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
8.阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
9.如图,在△ABC中,CE⊥AB于点E,BD⊥AC于点D,连接ED,求证:△ABC∽△ADE.
10.如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.
11.如图,AD∥BC,AE平分∠DAB,BE平分∠ABC.EF⊥AB,证明:△AEF∽△ABE.
12.如图,在直角三角形ABC中,∠C=90°,CD⊥AB,D是垂足,求证:△ACD∽△ABC.
13.如图,△ABC中,BE⊥AC于E,AD⊥BC于D.求证:△CDE∽△CAB.
14.已知:在Rt△ABC中∠C=90°,CD为AB边上的高.
求证:Rt△ADC∽Rt△CDB.
15.在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E.根据上述条件,请在图中找出四组相似三角形,并说明其中一组的理由.
16.已知:如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E为AC上一点,过E点作AC的垂线,交CD的延长线于点F,与AB交于点G.求证:△ABC∽△FGD.
17.已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.
(1)求证:△ABF≌△DAE;
(2)求证:△AMF∽△ADE;
(3)观察判断BF与AE有怎样的位置关系?
18.如图,在Rt△ABC中,CD是斜边AB上的中线,DF⊥AB,交AC于E,交BC的延长线于点F.
(1)求证:∠A=∠F;
(2)△CDE与△FDC是否相似?并给予证明.
19.如图,正方形AEFG的顶点E在正方形ABCD的边CD上,AD的延长线交EF于H点.
(1)试说明:△AED∽△EHD;
(2)若E为CD的中点,正方形ABCD的边长为4,求DH的长.
20.已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.
(1)求证:△ABF≌△DAE;
(2)找出图中与△ABM相似的所有三角形(不添加任何辅助线).
21.已知Rt△ABC中,直角边AC=3,BC=4,P、Q分别是AB、BC上的动点,且点P不与A、B重合.点Q不与B、C重合.
(1)若CP⊥AB于点P,如图1,△CPQ为等腰三角形,这时满足条件的点Q有几个?直接写出相等的腰和相应的CQ的长(不写解答过程)
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有几个?分别求出相应的CQ的长?
参考答案
1.证明:∵△ABC中,∠ACB=90°,F为AB的中点,
∴AF=CF,∠A+∠B=90°.
∴∠A=∠DCF.
∵EF⊥AB,
∴∠B+∠E=90°,
∴∠A=∠E,
∴∠E=∠DCF,
∴△CDF∽△ECF.
2.证明:∵AD⊥BC,
∴∠DAC+∠C=90°. (2分)
∵∠BAC=90°,
∴∠BAF=∠C. (2分)
∵OE⊥OB,
∴∠BOA+∠COE=90°. (2分)
∵∠BOA+∠ABF=90°,
∴∠ABF=∠COE. (2分)
∴△ABF∽△COE. (2分)
3.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB.
4.解:∵BD=2,AB=,BC=3.
∴=,==,
∴=,
而∠CBD=∠ABC,
∴△BCD∽△BAC.
5.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
6.解:△ACD∽△CBD 或△ACB∽△CDB或△ACB∽△ADC.
∵∠A+∠B=∠A+∠ACD=90°
∴∠B=∠ACD
∵∠CDB=∠ADC=90°
∴△ACD∽△CBD.
同法可证,△ACB∽△CDB或△ACB∽△ADC.
7.证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
8.解:(1)△ADE∽△FCD,理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD;
(2)由题意知,AD=CD=1,AE=.
在直角△DEA中,有DE===.
由(1)可得:=,则CF==.
9.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△ACE,
∴,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC.
10.证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠ADC=∠BEC,
而∠ACD=∠BCE,
∴△ACD∽△BCE.
11.证明:∵AE平分∠DAB,BE平分∠ABC,
∴∠FAE=∠DAB,∠ABE=∠ABC,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠BAE+∠ABE=90°,
∴∠AEB=90°,
∵EF⊥AB,
∴∠AFE=90°,
又∵∠BAE=∠BAF,
∴△AEF∽△ABE.
12.证明:∵在直角三角形ABC中,∠C=90°,CD⊥AB,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC.
13.证明:∵BE⊥AC于E,AD⊥BC,
∴点A、B、D、E四点共圆,
∴∠CDE=∠CAB,
又∵∠C=∠C,
∴△CDE∽△CAB.
14.证明:∵CD为AB边上的高,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∵∠ADC=∠CDB=90°,
∴Rt△ADC∽Rt△CDB.
15.解:△GCF∽△ABF,
△GDE∽△AED,
△GDE∽△ADC,
△GCF∽△AGD.
∵∠G=∠G,∠GCF=∠GDA,
∴△GCF∽△GDA.
16.证明:∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠FDG=90°,
∵EF⊥AC,
∴∠FEA=90°,
∴∠FEA=∠BCA.
∴EF∥BC,
∴∠FGB=∠B,
∴△ABC∽△FGD.
17.(1)证明:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=CD=AD,
∵CE=DF,
∴AF=DE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS);
(2)∵△ABF≌△DAE,
∴∠AFM=∠AED,
∵∠MAF=∠DAE,
∴△AMF∽△ADE;
(3)BF⊥AE.
理由:∵△AMF∽△ADE,
∴∠AMF=∠D=90°,
∴BF⊥AE.
18.(1)证明:∵∠ACB=90°,∴∠A+∠B=90°,
∵DF⊥AB,∴∠BDF=90°,
即∠B+∠F=90°,
∴∠A=∠F;
(2)解:△CDE∽△FDC.
理由是:∵CD是斜边AB上的中线,
∴AD=CD,
∴∠A=∠DCE,
∵∠DEC=∠A+∠ADE,∠DCF=∠DCE+∠ECF,
∴∠CED=∠FCD,
∴△CDE∽△FDC.
19.(1)证明:∵正方形AEFG和正方形ABCD中,∠AEH=∠ADC=∠EDH=90°,
∴∠AED+∠DEH=90°,∠AED+∠DAE=90°,
∴∠DEH=∠DAE.
∴△AED∽△EHD.
(2)解:∵正方形ABCD的边长为4,
∴AD=CD=4.
∵E为CD的中点,
∴DE=2.
∵△AED∽△EHD,
∴,
∴.
∴DH=1.
20.(1)证明:∵ABCD是正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°.
∵CE=DF,
∴AD﹣DF=CD﹣CE.
∴AF=DE.
在△ABF与△DAE中,
∴△ABF≌△DAE(SAS).
(2)解:与△ABM相似的三角形有:△FAM;△FBA;△EAD,
∵△ABF≌△DAE,
∴∠FBA=∠EAD.
∵∠FBA+∠AFM=90°,∠EAF+∠BAM=90°,
∴∠BAM=∠AFM.
∴△ABM∽△FAM.
同理:△ABM∽△FBA;△ABM∽△EAD.
21.解:(1)当CP为等腰三角形的底边时作CP的垂直平分线,交BC于Q,
则腰是CQ=PQ;
此时CQ=BC=2;
当CP为腰时,在BC上截取CQ=CP,
则腰是CP=CQ′,
此时CQ=CP==2.4;
当PC=PQ时,作PM⊥BC于M,则CM=MQ,
∵△CPM∽△ABC,
∴=,
∴=,
CM=,
CQ=2CM=.
综上所述,满足条件的点Q有3个,CQ的长为2或2.4或.
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有2个,
①△PQC∽△ACB时,
∴==,
∴CQ=BC=2,
②△CPQ″∽△BCA时,
∴,
∴,
∴CQ″=;
解答专项练习题(附答案)
1.已知:如图,△ABC中,∠ACB=90°,F为AB的中点,EF⊥AB.求证:△CDF∽△ECF.
2.如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,点O是AC边上一点,连接BO交AD于点F,OE⊥OB交BC边于点E.求证:△ABF∽△COE.
3.如图,在矩形ABCD中,E是AD边上的一点,BE⊥AC,垂足为点F.求证:△AEF∽△CAB.
4.如图,D是△ABC的边AB上的一点,BD=2,AB=,BC=3.求证:△BCD∽△BAC.
5.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
6.如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高,请指出其中一对相似三角形并证明之.
7.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
8.阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
9.如图,在△ABC中,CE⊥AB于点E,BD⊥AC于点D,连接ED,求证:△ABC∽△ADE.
10.如图,△ABC中,AB=AC,D是BC中点,BE⊥AC于E,求证:△ACD∽△BCE.
11.如图,AD∥BC,AE平分∠DAB,BE平分∠ABC.EF⊥AB,证明:△AEF∽△ABE.
12.如图,在直角三角形ABC中,∠C=90°,CD⊥AB,D是垂足,求证:△ACD∽△ABC.
13.如图,△ABC中,BE⊥AC于E,AD⊥BC于D.求证:△CDE∽△CAB.
14.已知:在Rt△ABC中∠C=90°,CD为AB边上的高.
求证:Rt△ADC∽Rt△CDB.
15.在矩形ABCD中,F是BC上一点,AF的延长线交DC的延长线于G,DE⊥AG于E.根据上述条件,请在图中找出四组相似三角形,并说明其中一组的理由.
16.已知:如图,在△ABC中,∠ACB=90°,过点C作CD⊥AB于点D,点E为AC上一点,过E点作AC的垂线,交CD的延长线于点F,与AB交于点G.求证:△ABC∽△FGD.
17.已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.
(1)求证:△ABF≌△DAE;
(2)求证:△AMF∽△ADE;
(3)观察判断BF与AE有怎样的位置关系?
18.如图,在Rt△ABC中,CD是斜边AB上的中线,DF⊥AB,交AC于E,交BC的延长线于点F.
(1)求证:∠A=∠F;
(2)△CDE与△FDC是否相似?并给予证明.
19.如图,正方形AEFG的顶点E在正方形ABCD的边CD上,AD的延长线交EF于H点.
(1)试说明:△AED∽△EHD;
(2)若E为CD的中点,正方形ABCD的边长为4,求DH的长.
20.已知:正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M.
(1)求证:△ABF≌△DAE;
(2)找出图中与△ABM相似的所有三角形(不添加任何辅助线).
21.已知Rt△ABC中,直角边AC=3,BC=4,P、Q分别是AB、BC上的动点,且点P不与A、B重合.点Q不与B、C重合.
(1)若CP⊥AB于点P,如图1,△CPQ为等腰三角形,这时满足条件的点Q有几个?直接写出相等的腰和相应的CQ的长(不写解答过程)
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有几个?分别求出相应的CQ的长?
参考答案
1.证明:∵△ABC中,∠ACB=90°,F为AB的中点,
∴AF=CF,∠A+∠B=90°.
∴∠A=∠DCF.
∵EF⊥AB,
∴∠B+∠E=90°,
∴∠A=∠E,
∴∠E=∠DCF,
∴△CDF∽△ECF.
2.证明:∵AD⊥BC,
∴∠DAC+∠C=90°. (2分)
∵∠BAC=90°,
∴∠BAF=∠C. (2分)
∵OE⊥OB,
∴∠BOA+∠COE=90°. (2分)
∵∠BOA+∠ABF=90°,
∴∠ABF=∠COE. (2分)
∴△ABF∽△COE. (2分)
3.证明:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于点F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB.
4.解:∵BD=2,AB=,BC=3.
∴=,==,
∴=,
而∠CBD=∠ABC,
∴△BCD∽△BAC.
5.(1)证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD:AC=AC:AB,
∴AC2=AB AD;
(2)证明:∵E为AB的中点,
∴CE=BE=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD,
∴△AFD∽△CFE.
6.解:△ACD∽△CBD 或△ACB∽△CDB或△ACB∽△ADC.
∵∠A+∠B=∠A+∠ACD=90°
∴∠B=∠ACD
∵∠CDB=∠ADC=90°
∴△ACD∽△CBD.
同法可证,△ACB∽△CDB或△ACB∽△ADC.
7.证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
8.解:(1)△ADE∽△FCD,理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD;
(2)由题意知,AD=CD=1,AE=.
在直角△DEA中,有DE===.
由(1)可得:=,则CF==.
9.证明:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
∵∠A=∠A,
∴△ABD∽△ACE,
∴,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC.
10.证明:∵AB=AC,D是BC中点,
∴AD⊥BC,
∴∠ADC=90°,
∵BE⊥AC,
∴∠BEC=90°,
∴∠ADC=∠BEC,
而∠ACD=∠BCE,
∴△ACD∽△BCE.
11.证明:∵AE平分∠DAB,BE平分∠ABC,
∴∠FAE=∠DAB,∠ABE=∠ABC,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴∠BAE+∠ABE=90°,
∴∠AEB=90°,
∵EF⊥AB,
∴∠AFE=90°,
又∵∠BAE=∠BAF,
∴△AEF∽△ABE.
12.证明:∵在直角三角形ABC中,∠C=90°,CD⊥AB,
∴∠ADC=∠ACB=90°,
∵∠A=∠A,
∴△ACD∽△ABC.
13.证明:∵BE⊥AC于E,AD⊥BC,
∴点A、B、D、E四点共圆,
∴∠CDE=∠CAB,
又∵∠C=∠C,
∴△CDE∽△CAB.
14.证明:∵CD为AB边上的高,
∴∠ADC=∠CDB=90°,
∵∠ACB=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∵∠ADC=∠CDB=90°,
∴Rt△ADC∽Rt△CDB.
15.解:△GCF∽△ABF,
△GDE∽△AED,
△GDE∽△ADC,
△GCF∽△AGD.
∵∠G=∠G,∠GCF=∠GDA,
∴△GCF∽△GDA.
16.证明:∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠FDG=90°,
∵EF⊥AC,
∴∠FEA=90°,
∴∠FEA=∠BCA.
∴EF∥BC,
∴∠FGB=∠B,
∴△ABC∽△FGD.
17.(1)证明:∵四边形ABCD是正方形,
∴∠BAF=∠D=90°,AB=CD=AD,
∵CE=DF,
∴AF=DE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS);
(2)∵△ABF≌△DAE,
∴∠AFM=∠AED,
∵∠MAF=∠DAE,
∴△AMF∽△ADE;
(3)BF⊥AE.
理由:∵△AMF∽△ADE,
∴∠AMF=∠D=90°,
∴BF⊥AE.
18.(1)证明:∵∠ACB=90°,∴∠A+∠B=90°,
∵DF⊥AB,∴∠BDF=90°,
即∠B+∠F=90°,
∴∠A=∠F;
(2)解:△CDE∽△FDC.
理由是:∵CD是斜边AB上的中线,
∴AD=CD,
∴∠A=∠DCE,
∵∠DEC=∠A+∠ADE,∠DCF=∠DCE+∠ECF,
∴∠CED=∠FCD,
∴△CDE∽△FDC.
19.(1)证明:∵正方形AEFG和正方形ABCD中,∠AEH=∠ADC=∠EDH=90°,
∴∠AED+∠DEH=90°,∠AED+∠DAE=90°,
∴∠DEH=∠DAE.
∴△AED∽△EHD.
(2)解:∵正方形ABCD的边长为4,
∴AD=CD=4.
∵E为CD的中点,
∴DE=2.
∵△AED∽△EHD,
∴,
∴.
∴DH=1.
20.(1)证明:∵ABCD是正方形,
∴AB=AD=CD,∠BAD=∠ADC=90°.
∵CE=DF,
∴AD﹣DF=CD﹣CE.
∴AF=DE.
在△ABF与△DAE中,
∴△ABF≌△DAE(SAS).
(2)解:与△ABM相似的三角形有:△FAM;△FBA;△EAD,
∵△ABF≌△DAE,
∴∠FBA=∠EAD.
∵∠FBA+∠AFM=90°,∠EAF+∠BAM=90°,
∴∠BAM=∠AFM.
∴△ABM∽△FAM.
同理:△ABM∽△FBA;△ABM∽△EAD.
21.解:(1)当CP为等腰三角形的底边时作CP的垂直平分线,交BC于Q,
则腰是CQ=PQ;
此时CQ=BC=2;
当CP为腰时,在BC上截取CQ=CP,
则腰是CP=CQ′,
此时CQ=CP==2.4;
当PC=PQ时,作PM⊥BC于M,则CM=MQ,
∵△CPM∽△ABC,
∴=,
∴=,
CM=,
CQ=2CM=.
综上所述,满足条件的点Q有3个,CQ的长为2或2.4或.
(2)当P是AB的中点时,如图2,若△CPQ与△ABC相似,这时满足条件的点Q有2个,
①△PQC∽△ACB时,
∴==,
∴CQ=BC=2,
②△CPQ″∽△BCA时,
∴,
∴,
∴CQ″=;
